基于智能手机传感器的林区行人定位算法

王瀚庆，武 刚，陈玥璐，陈飞翔

(北京林业大学 信息学院，北京 100083)

0 引 言

步行是人们在林区实施森林调查，培育和经营作业，执行抢险、救援任务，开展科学研究和进行休闲游憩活动的重要方式，林区行人导航存在广泛的应用需求[1]。定位是基于位置服务(location based service，LBS)的基础，是行人导航的重要部分，因此实现林区精准定位具有重要意义[2]。虽然全球卫星导航系统(global navigation satellite system, GNSS)在定位、导航方面具有广泛应用，但由于卫星容易受到多路径效应、地形与地物的遮挡等因素的影响，导致其精度降低，不能满足绝大多数森林资源与环境监测定位的精度要求[3-6]。因此，探索无信号情况下的林区行人定位具有研究价值和应用意义。

在脱离GNSS信号与移动网络信号的前提下，可以采用的定位方式包括：有源定位技术和无源定位技术[7]。前者需要添加额外硬件设施，系统部署复杂，不适用于林区[8]。后者利用携带式惯性测量单元(inertial measurement unit, IMU),计算相对位置信息。随着智能手机内置传感器技术的提升，有学者提出基于智能手机传感器的定位方法[9]，其中，针对行人定位主要采用的方法为行人航位推算算法[10-12](pedestrian dead reckoning，PDR)。PDR算法以行人每步为单位进行步长和方向估计，以此计算每步相对位置。然而，受手机传感器精度限制，基于手机传感器的PDR算法不能直接适用于林区行人定位：一方面，在复杂且没有外界参考的环境下获得精准的方向[13]和步长[14]是PDR算法的难点；另一方面，林区路况复杂，PDR算法无法满足获取高程分量的定位需求。

本文基于改进的PDR算法提出林区行人定位(forest-pedestrian location，FPL)算法。针对行人方位角和步长测量精度低的问题，首先提出融合多传感器输出多滤波算法组合的方法，提高行人位移方位角求解精度；其次，采用K邻近(K-nearest neighbor, KNN)算法估算行人实时步长。在此基础上，使用差分气压测高法获取行人高程信息。

1 FPL算法的基本原理

FPL算法流程如图1所示：①使用扩展卡尔曼滤波(extended Kalman filter, EKF)融合算法融合加速度计和磁力计输出，求解原始方位角；②使用卡尔曼滤波(Kalman filter, KF)融合算法，融合陀螺仪输出，算出精准方位角；③采用差分气压测高[15]，根据气压计输出，测量行人每步高度变化；④结合计时器和加速度计输出，使用KNN算法，估算行人步长；⑤根据PDR算法，获取行人2维定位位置；⑥最后利用气压计获取行人在林区的高程信息。

图1 FPL算法Fig.1 FPL algorithm

以行人GPS定位信息丢失前的最后一个定位点为起始点，持续跟踪行人定位信息。2维坐标采用投影坐标系，北方向为y轴正方向，记为N；东方向为x轴正方向，记为E。位移方向与y轴正方向夹角为方位角。行人位置计算公式为

(1)

(1)式中：(Ei,Ni)为行人第i步的2维坐标；(E0,N0)为行人丢失GPS定位信息的最后一个点的2维坐标；li为第i步步长；θi为第i步方向角。以起始点高度平面为基准高度h0，第i步高度为：hi=h0+h，则第i步行人3维定位坐标为(Ei,Ni,hi)。

2 FPL算法的设计

2.1 基于多传感器的方位角估计

方位角误差是PDR算法及FPL算法中位置估计误差的最主要来源。方位角分为实时方位角和位移方位角，其中实时方位角为行人进行一个跨步过程中每一时刻的方向值，位移方位角为行人完成一个跨步后相对上一个落脚点的方向值。为了能够精准测量实时方位角数据，采用EKF算法融合加速度计和磁力计输出求实时方位角θ。侧倾角φ，俯仰角ψ和实时方位角θ可由(2)式求解得到[16]为

(2)

(2)式中：ax,ay,az分别为加速度计沿手机坐标系x轴,y轴,z轴方向输出测量值；mx,my,mz为磁力计沿手机坐标系x轴,y轴,z轴方向输出测量值。

θk|k-1=θk-1+Δθ+Wk

(3)

状态估计方程为

(4)

(3)—(4)式中：θk|k-1为方位角预测值;Wk为预测方差,Kk为KF增益矩阵;H是测量参数。

根据行人生理学特征，行人自然行走过程中，实时方位角的变化过程如图2所示，以位移方位角为中轴，做周期性波动，周期为1复步时间间隔。由图3所示分位图(quantile-quantile plot, Q-Q)可知，每一周期内，实时方位角数值的概率分布满足正态分布。因此，可利用t分布，根据小样本容量的实时方位角估计1复步时间间隔之内的位移方位角[17]。

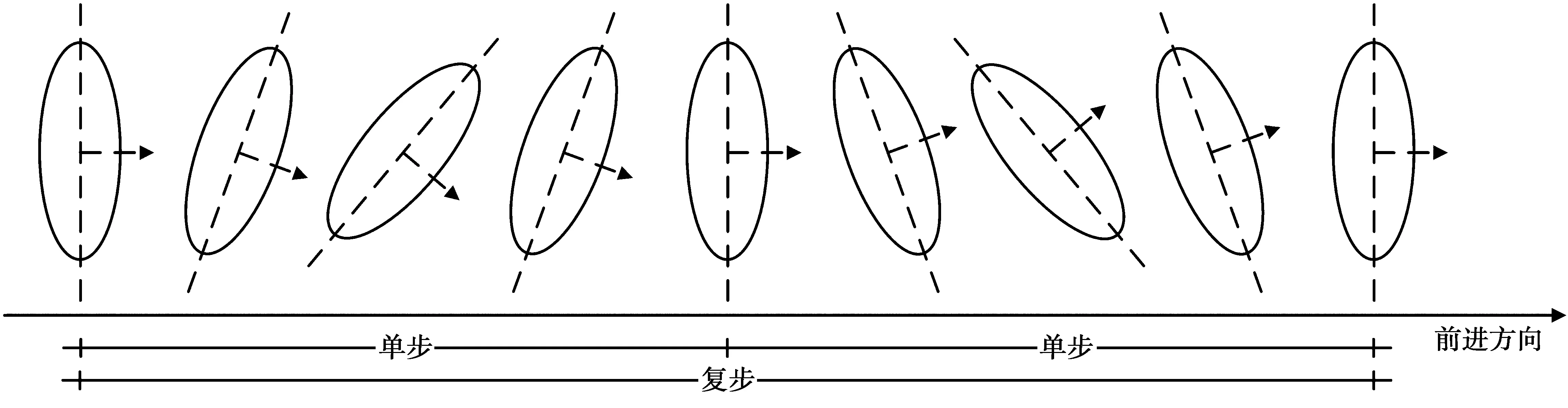
图2 行走过程中身体方向变化Fig.2 Changes in body direction during stepping process

图3 方位角Q-Q图Fig.3 Q-Q plot of azimuth

采集到的实时方位角包括：行人的朝向、行人身体的自然摆动、行人手持手机时身体的抖动、手机传感器的测量误差等。测量数据变化十分迅速，包含相当窄的峰值，如果滤波器窗口长度大于峰值间隔，会造成方向数据过分平滑。Savitzky-Golay(S-G)滤波[18]是一种有限脉冲响应平均滤波器，可以保留信号的高频成分，适用于行人导航中信号的过滤[19]。因此，根据实时方位角确定位移方位角步骤为

1)取1单步时间间隔内，实时方位角均值；

2)采用S-G滤波，对1)所得数据进行平滑处理；

3)使用KF滤波对2)所得数据进行最后的平滑处理。

行人实时方位角如图4所示，当行人向北行走时，实时方位角在360°与0°之间快速跳跃，若直接使用上述步骤计算，将导致较大偏差。因此，当行人位移方向朝向北方附近时，首先针对实时方位角求解正弦值与余弦值；其次，针对实时方位角计算三角函数值；最后，采用上述方法计算位移方位角三角函数值。

2.2 基于KNN算法步长估计

本文采用KNN学习算法估计行人步长。将行人行走时产生的行为数据形式化为特征向量，称之为步长特征K。K包括一单步之内加速度均值amean、加速度方差avar、步频f及高度变化h，即K=(amean,avar,f,h)。假设在林区不同的路面情况、不同的行走方式共有m种状态，记L={l1,l1,…,lm}代表不同状态下的步长集合。按(K,li)键值对形式存储数据，建立步长模型数据库，假定共有n项步长特征，则步长模型数据库中不超过nm种步长模型集合，其中liL。实验表明，为排除硬件误差，保留(N/4,3N/4)区间内的数据，可以提高数据精度且可以保证匹配精准度[7]。

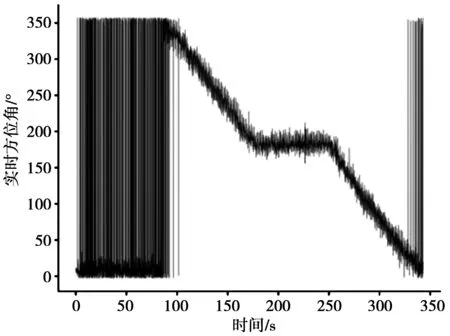
图4 行走过程中实时方位角Fig.4 Azimuth during walking process

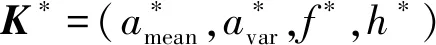
(5)

实验证明，步行特征中不同属性的重要性呈现差异性，因此引入属性权重ωi(i=1,2,…,k)，得到最终距离度量为

(6)

步长估计步骤为：

1)计算K*与Kj之间的距离度量dist2(K*,Kj)，其中j=1,2,…,n；

2)按升序排列dist2(K*,Kj)，查找前k项对应的K；

3)在步长模型数据库中，根据(K,li)查找前k项步长l；

步骤4)中，权重为[20]

(7)

(7)式中：e是正无穷小量；1/(disti+e)为估计点到第i个距离最近的数据库点的欧式距离倒数。

2.3 差分气压测高

智能手机中压力传感器精度较高，同时，林区步行环境满足Laplace压高方程成立条件，因此，可以采用差分气压测高，解决林区3维定位中高程测算的问题。差分气压测高利用Laplace公式：若已知参考点高度为h0，气压值为P0，温度为t0，则有

(8)

(8)式中：Rd为气体常数；g为所在位置的重力加速度值；h,P,t分别为待测点高度、气压值及温度；T=(t+t0)/2为待测点与参考点之间的平均温度。当行人在林区行走时，行人所处位置重力加速度g、平均温度T及初始气压值P0有确定关系，因此(8)式可化简为

Δh=h-h0=a·lnP+b

(9)

由(9)式可建立针对确定位置确定温度环境下的高度关于气压的一元线性估计模型。由于重力加速度变化较小，在行人行走高度上温度几乎不变，因此，在确定温度条件下，该一元线性模型具有便捷度及普适性，根据(8)—(9)式可以获得行人当前位置高度值h。

3 实验结果与分析

3.1 实验条件

本文以小米Note作为传感器数据测量工具，通过Android传感器编程调用SensorManger接口，获取相应传感器数据，选择北京鹫峰国家森林公园作为实验地点，进行实验分析。传感器数据包括加速度计输出、磁力计输出、陀螺仪输出以及气压计输出。行人自然步行的频率为75～125步/min，普通人的步长分布在50～90 cm[21-22]。因此，行走的速度为0.7～1.8 m/s，步行频率为1.25～2.08 Hz，根据采样定理，采样频率取60 Hz，可以保证信息不丢失[14]。本算法实验中，实验者手持智能手机，以正常行走速度、姿态进行步行实验，同时以60 Hz获取传感器原始数据。

实验环境如图5所示。实验时，先针对每一种路况分别进行仿真分析，包括上坡、下坡、台阶、平面道路及林间无路环境。最后选择实验路径如图5中黑色轨迹，进行最终仿真实验分析，所选实验路况为下坡方向，包含直行转弯、台阶、缓坡等路况，具有一定的林区步行环境代表性。

图5 实验环境Fig.5 Experimental environment

3.2 实验结果分析

在PDR算法中，方向信息常用电子罗盘(磁力计与加速度计组合)输出的方式获取；步长L常用非线性步长模型估计，表达式为

(10)

(10)式中：amax,I,amin,i为单步加速度最大值与最小值；C为步长相关系数。

本文将FPL算法与使用上述获取方向、步长信息方式的定位方法进行对比。首先，讨论步长估算模型中KNN算法中K值与权重的选择；其次，确定K值与权重后，依次选择3.1节所述的5种步行环境作为步行条件，作为实验环境进行实验，将FPL定位算法与如下3种定位方式对比：电子罗盘估计方向与KNN算法估计步长组合法(记为MKNN)、电子罗盘估计方向与非线性模型估计步长组合法(记为MNRA)、多传感器多次融合法估计方向与非线性模型估计步长组合法(记为SNRA)；最后，选择复杂林区步行环境，进行仿真分析。

表1是不同K值及权重模式下的步长估计误差。其中weights为KNN算法中取最近K项加权均值时的权重，weights=distance为(7)式所述权重，weights=uniform为所有数据项权重相同。

由表1可知，选择加权KNN算法，当K=5时，KNN算法对步长的估算误差较低，精度优于其他K值情况，因此，本文KNN算法中，权重选择(7)式，K取值为5。得到K值之后，后续仿真分析均以此参数进行分析。

表1 不同K值下KNN对比

FPL定位实验前，进行高程实验，验证气压计测高在实际中的可用性。选取林区不同路况，包括上坡、下坡以及台阶路段，以起始点为基准高度，手持智能手机随机以不同的速度进行步行数据测量。图6a为不同路况下气压计输出情况，图6b所示为行人行走时每时刻计算出的高度变化理想效果，平均行走100 m误差在±5 m之内，可以满足林区行人定位的高程分量需求。

FPL算法分路况实验时，每种路况选择约500 m进行步行实验，所有定位方法采用同一份原始数据进行误差分析。实验中，以起始点高度为基准点，根据气压计输出，利用差分气压测高测量行人在林区的高程信息。3维定位误差情况如表2所示。

表2的实验结果表明，在上坡、下坡、台阶、平面道路、林间无路环境下，FPL定位算法与其余定位方式相比均能表现出较高精度。

最后，本文选取包含多种路况的路径进行仿真分析。由图7可知，本文提出的林区行人定位算法得到的行人轨迹更接近真实轨迹。PDR算法中误差主要来源是方位角的误差，本文提出的融合多传感器输出测量实时方位角，多滤波方法组合确定最终位移方向的方法，可以有效地提高方位角精度，从而提高定位精度。从图8可知，本文所提出的FPL算法行走1 000 m最大误差为41 m，误差为4%，可以满足定位需求。

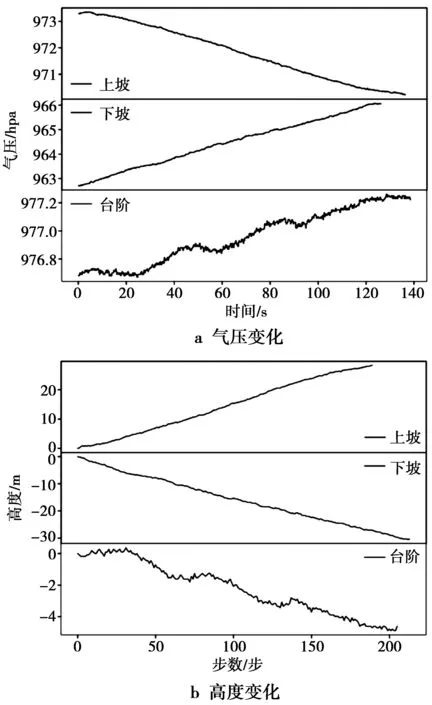
图6 不同路况下气压及高度变化Fig.6 Pressure changes and height changes under different road condition

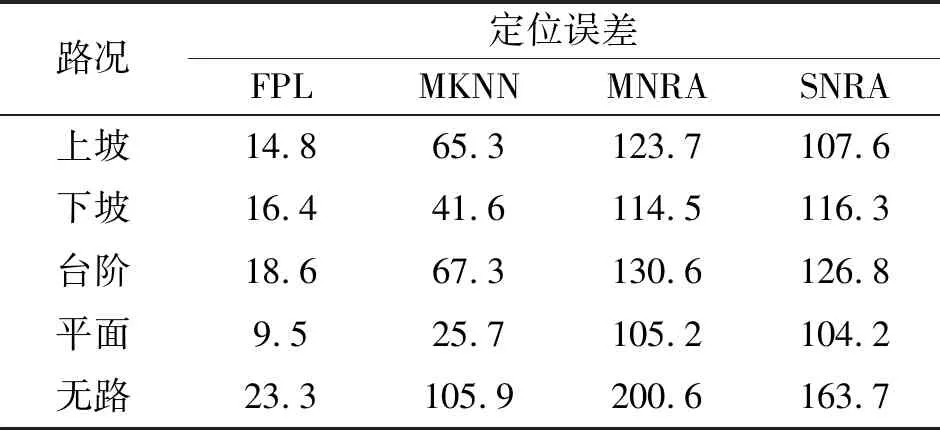
Tab.2 positioning accuracy of FPL，MKNN，MNRA and SNRA under different pedestrian environment comparison m

图7 行走轨迹结果Fig.7 Schematic diagram of pedestrian walking trajectories

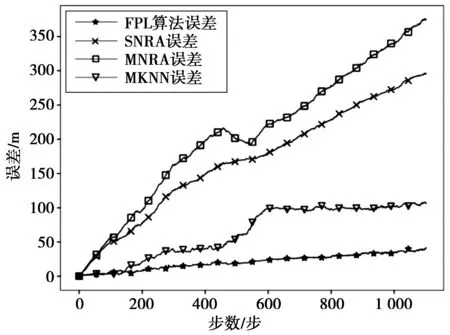
图8 行人定位误差Fig.8 Pedestrian localization errors

4 结 语

本文提出的FPL定位算法使用智能手机传感器作为实验数据测量工具。针对PDR算法精度不高的问题，从方位角和步长2个方面进行改进。采用融合多传感器输出方法，提高实时方位角测量精度，同时使用多种滤波组合方法，提高行人位移方位角的估算精度；采用KNN算法估计行人步长，以提高步长估计的准确性和适用性，在此基础上，利用差分气压测高增加行人高程定位信息。实验证明，本算法可以有效提高2维定位精度，同时可以获得完整的3维定位信息，最终，将定位误差控制在5%以内，适用于林区行人定位。未来的工作重点将从以下2个方面展开：①更有效的陀螺仪校正方法，提高方位角精度；②有效利用KNN算法降维的方法，提高步长解算的效率和精度。