基于刀盘扭转能量的土压平衡盾构刀具磨损分析
2019-09-05荣雪宁王明洋戎晓力
荣雪宁, 卢 浩, 王明洋,, 文 祝, 戎晓力, 王 振
(1. 南京理工大学 机械工程学院, 南京 210094; 2. 陆军工程大学 爆炸冲击防灾减灾国家重点实验室, 南京 210007)
刀具磨损是土压平衡盾构施工的重要风险因素[1].在磨损性地层中掘进时,刀具损耗较快,因此需及时换刀.开舱换刀不仅影响工程进度,增加工程造价,而且具有一定的危险性[2].为合理组织换刀工作,预估刀具的磨损情况是一项重要的任务.理论上,盾构机的实时掘进参数能反映刀具的磨损状态,有研究者通过考察转矩、推力以及掘进速度等参数预测了刀具的磨损状态或磨损速率[3-5].由于转矩等施工参数的波动性较大且影响因素较多,该方法尚不能用于实际施工中刀具磨损的估计.另外,有研究采用超声波对刀具进行直接检测发现,超声检测系统能较准确地反映单把刀具的磨损情况[6].然而,盾构刀盘上有上百把刀具,只有少数刀具能安装超声检测系统,因此,该方法的应用受到限制.目前,为判断刀具磨损的总体情况,仍需开舱检查.
为确定开舱检查的时机,工程中常采用日本隧道协会提出的JTS公式δ=kπDnL/v(k为土层条件决定的磨损系数;D盾构机外径;n为刀盘转速;L为盾构机掘进距离;v为盾构掘进速度)预测刀具的磨损量[7].JTS公式应用广泛,却也有其局限性[8].首先,该公式要求k,n和v均为常数,而实际施工过程中只有n比较稳定,k和v的变化性较大.考虑到式中参数的波动性,Li等[8]采用了区间变量分析方法确定δ的取值范围.然而,在卵石层等不均匀地层中掘进时,经常需要破碎硬质岩石.此情况下,实际掘进速度的下限趋近于0,而通过区间运算得出的磨损量上限趋近于无穷大,所以该公式很难为实际工程中刀具磨损的估计提供参考价值.此外,JTS公式预测的磨损量实际为土层参数与刀具沿环向切割距离的乘积.刀盘每旋转1周,其沿隧道轴向的位移仅为0~70 mm[9],刀具的环向切割距离约为刀具在土层中的滑动位移.由磨损理论可知,材料的磨损量不仅与材料的特性和滑动位移有关,还与接触面的载荷或摩擦力有关[10].在同样的土层条件和滑动位移下,刀具与土层间的受力情况不同会导致刀具磨损量的差异.而JTS公式并未考虑刀具与土层间的实际受力情况,因此缺少一个衡量刀具磨损量的重要参数.
目前,一些盾构设备安装了施工参数自动采集系统,以对刀盘转矩、刀盘转速和盾构机的掘进速度等参数进行实时监控和记录[11].其中刀盘转矩是反映刀盘与土体摩擦力大小的重要参数,可用于刀具磨损的计算.本文分析了成都地铁盾构20个区间、总掘进距离约14 km的施工数据,建立了一种基于刀盘扭转能量的刀具磨损预测模型.该模型可用于估计刀具的磨损情况,为换刀时机的选择和换刀数目的预测提供参考.盾构区间穿越地层可分为两类:24个换刀点的穿越地层为卵石,6个换刀点的穿越地层为中风化泥岩.
1 刀盘扭转能量与刀具磨损
根据能量磨损理论,刀具磨损体积(Vw)正比于刀具与土体间的摩擦功(Wf)[10]:
(1)
式中:ER为磨损的能量密度,即单位体积磨损所消耗的能量,其数值与刀具材料有关.Wf由刀具对土体的切削转矩(Tc)沿刀盘旋转角度进行积分而得.记刀盘旋转的总时间为tr,则有
(2)
盾构机记录的是刀盘总转矩[9]:
T=Tb+Tc+Tm+T0
(3)
式中:Tb为刀盘面板与土体之间的摩擦转矩;Tm为土体搅拌转矩;T0为刀盘空转阻力转矩,T0与其他各项无关,可视为常量且对总转矩的贡献很小[12].Tb,Tc和Tm具有正相关性,三者都与土体受到的挤压程度有关,故可认为Tc∝T.令WT为掘进期间的刀盘扭转能量,
(4)
式中:Ti,ni分别为第i个采样点的实测转矩和刀盘转速;Δti为该采样点处的时间间隔,一般为10~50 s;K为采样点总数.由于Wf∝WT,根据式(1)可知Vw和WT呈线性关系.

图1 成都地铁土压平衡盾构典型刀盘布置Fig.1 Typical tools arrangement on the cutterhead of earth pressure balance shield machine for Chengdu Metro
成都地铁的典型土压平衡盾构刀盘布置如图1所示.其中:滚刀的直径为432 mm;滚刀超出刀盘面板的高度为175 mm;刮刀和撕裂刀超出刀盘面板的高度为120~125 mm.在盾构掘进中,滚刀对其他两种刀具产生保护作用,因此承担了大部分刀具磨损.换刀记录表明,滚刀的更换数目占全部换刀数目的90%以上,故本文用刀具更换数目(Nc)作为刀具磨损体积的指标.
刀盘扭转能量与换刀数目的关系如图2所示.其中:图2(a)为全部换刀点Nc与WT的关系;图2(b)中按照地层类型对数据点进行了区分;R2为线性拟合的决定系数.由图2(a)可知,换刀数目与刀盘扭转能量基本呈线性关系.由图2(b)可知,两种不同类型地层的数据点比较接近,说明该能量-磨损关系对于成都地铁穿越的卵石和中风化泥岩地层都具有一定的适用性.
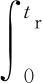
现有研究一般认为刀具的磨损程度与其切割线的距离有关[5].刀具的实际切割线为螺旋线,由于施工贯入度一般小于隧道直径的1%,所以该螺旋线的长度约为刀具环向运动的距离,该距离与刀盘旋转的角位移(θ)对应.本文研究的盾构区间刀盘角位移与换刀数目的关系如图3所示.可以看出,换刀数目与刀盘角位移基本呈线性关系.这表明,基于刀具切割线距离预测刀具的磨损程度是可行的.
工程中常根据地层类型和掘进距离预测刀具的磨损情况[13-14].图4给出了30个换刀点Nc与L的关系.其中图4(a)为全部换刀点Nc与L的关系.图4(b)中按照地层类型对数据点进行了区分,并对两种地层中的数据分别进行了线性拟合.由图4(a)可见,换刀数目与掘进距离的关系比较离散,R2较小,为0.303.由图4(b)可见,在类似的地层下掘进相同距离,刀具磨损情况存在较大的差异.两种地层拟合函数的决定系数都较小(卵石R2=0.440,中风化泥岩R2=0.273).相较于掘进距离,采用刀盘扭转能量作为刀具磨损的预测参数更为可靠,也更符合摩擦学理论.

图2 换刀数目与刀盘扭转能量的关系Fig.2 Relationship between number of cutter replaced and torque energy
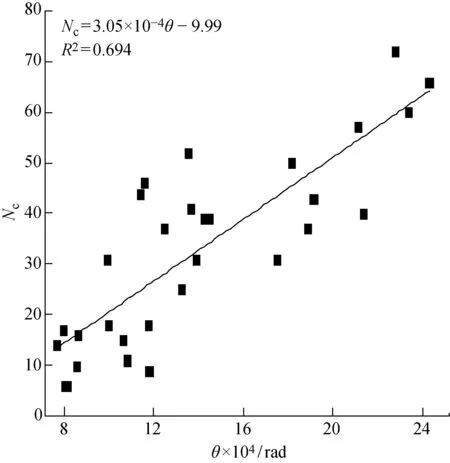
图3 换刀数目与刀盘角位移的关系Fig.3 Relationship between number of cutter replaced and angular displacement of cutterhead
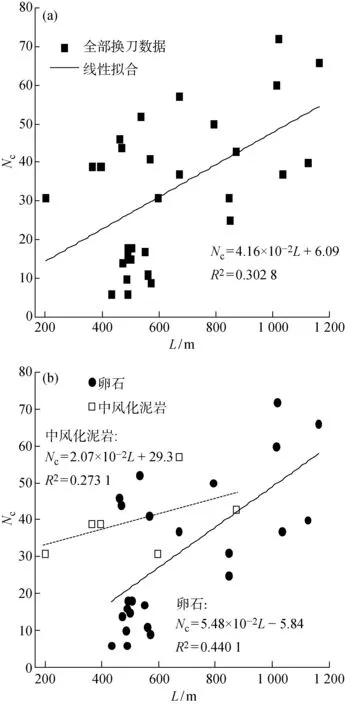
图4 换刀数目与掘进距离的关系Fig.4 Relationship between number of cutter replaced and excavated length
3 刀具磨损的双参数预测模型
刀盘前表面分布有泡沫喷头,增加泡沫添加剂的含量能显著减少刀具磨损[15-16],故泡沫添加剂的流量可能影响对刀具磨损体积.本文在刀盘扭转能量的基础上增加泡沫添加剂体积参数,以建立刀具磨损的双参数预测模型.在施工中,盾构机实时记录4个泡沫管路的泡沫添加剂流量.本文采用的泡沫添加剂体积(Vadd)是4个管路的流量总和:
(5)
式中:q1,q2,q3以及q4分别为4个泡沫管路中实时记录的添加剂流量.换刀数目与刀盘扭转能量以及泡沫添加剂体积的关系如图5所示.
图5 换刀数目与刀盘扭转能量和泡沫添加剂体积的关系Fig.5 Relationship between number of cutter replaced, torque energy and volume of foaming liquid
从图5可以看出,换刀数目与刀盘扭转能量正相关,与泡沫添加剂体积负相关,可用二元线性回归模型描述Nc,WT以及Vadd的关系:
Nc=aWT+bVadd+c
(6)
式中:a,b和c为回归系数.采用30个换刀点的数据进行拟合得到的a,b和c的数值及其标准差、t检验值和P检验值见表1.可以看出,a,b的P值都远小于0.05,表明换刀数目与刀盘扭转能量、泡沫添加剂体积的回归关系具有统计显著性.双参数模型的R2为0.822,大于单参数模型,这说明,增加泡沫添加剂体积改善了磨损模型的预测精度.
表1 刀具磨损双参数预测模型的回归系数
Tab.1 Fitting parameters of the prognosis model for cutter wear

类别abcR2数值7.68×10-8-2.60×10-6-2.780.822标准差6.89×10-98.08×10-7—t检验值11.152-3.2622—P检验值1.3×10-112.99×10-3—

图6 换刀数目预测值与实际值的对比Fig.6 Comparison of predicted and actual numbers of cutter replaced

4 不同地层类型的刀具磨损预测模型
为考察地层类型对双参数模型的影响,分别将卵石和中风化泥岩地层中的数据进行拟合,预测模型仍采用式(6).卵石和中风化泥岩地层中的数据拟合结果分别见表2和3.不设定截距时,中风化泥岩地层中的数据将得出1个正常数项c.为避免模型预测始发端出现磨损,表3中将c值设定为0.从表2和3可以看出,两种地层中的换刀数目都符合式(6)的二元线性关系,决定系数分别为0.870和0.983,P检验值均小于0.05.两种地层的a差别不大,中风化泥岩地层中的b是卵石层中b的3倍左右.这表明中风化泥岩地层中的换刀数目相对于Vadd更加敏感,由于该地层数据点较少,该理论的确认还需要进一步的研究.
表2 卵石地层磨损预测模型回归系数
Tab.2 Fitting parameters of the prognosis model for cutter wear in gravel

类别abcR2数值7.76×10-8-2.13×10-6-5.880.870标准差6.58×10-97.79×10-7—t检验值11.79-2.730—P检验值1.01×10-100.0120—
表3 中风化泥岩地层预测模型回归系数
Tab.3 Fitting parameters of the prognosis model for cutter wear in intermediately weathered mudstone/sandstone

类别abcR2数值9.39×10-8-6.83×10-600.983标准差8.85×10-92.57×10-6—t检验值10.61-2.660—P检验值4.46×10-45.64×10-2—
5 结论
(1) 土压平衡盾构的刀具磨损体积与刀盘扭转能量密切相关.采用刀盘扭转能量预测换刀数目比根据土层类型和掘进距离预测换刀数目更加准确.
(2) 在刀盘扭转能量的基础上增加泡沫添加剂体积参数并建立二元线性模型能进一步优化刀具磨损的预测精度.根据全部30个换刀点建立的二元回归模型决定系数为0.822,显著高于只采用能量、切割线距离或掘进距离的单参数模型决定系数.换刀数目与刀盘扭转能量正相关,与泡沫添加剂体积负相关.两个变量的回归系数P检验值均远小于0.05.
(3) 卵石层和中风化泥岩地层中的换刀数目都基本符合双参数预测模型.相对于卵石地层,在中风化泥岩地层中增加泡沫添加剂用量能更显著地减少刀具磨损.
