混合遗传算法求解多中心联合配送路径问题

2019-09-05范厚明徐振林刘文琪

上海交通大学学报 2019年8期

范厚明，徐振林，李阳，刘文琪，耿静

(大连海事大学 a. 交通运输工程学院； b. 战略管理与系统规划研究所，辽宁大连 116026)

面对激烈的市场竞争，物流配送企业追求的目标已经从仅要求完成配送任务转变为要求在保证配送任务完成的基础上，通过整合资源，提高资源利用率，降低配送总成本.车辆路径问题(Vehicle Routing Problem，VRP) 是物流配送企业运营管理的核心问题，VRP自提出以来，陆续有研究人员提出各种拓展模型并对其进行了深入研究.经典VRP是针对一系列已知地理位置的客户，设计出满足一定约束条件的行车路线进行送货服务(或收货服务)，以使得整个物流服务过程达到期望的目标(如费用最低、路径最短等).

随着业务的拓展，一些连锁超市、快递企业或快消企业等为降低远距离配送引起的高额成本以及提高配送时效，会选择在某一区域内设有多个配送中心联合完成企业的配送业务.此类配送模式可归结为多中心车辆路径问题(Multi-depot Vehicle Routing Problem，MDVRP)，MDVRP作为经典VRP的一类拓展问题，是工程技术、经济管理、信息科学等诸多领域内很多复杂问题的集中概括和简化形式，有着重要的实际利用价值.鉴于此，近些年许多研究人员对此类问题进行了深入研究.由于MDVRP属于非确定性多项式(Non-deterministic Po-lynomial, NP)完全类问题，传统的精确算法不太适用于较大规模问题的求解，而各类启发式算法则在此方面有着不错的表现，如Allahyari等[1]应用自适应贪婪随机算法、Oliveira等[2]应用合作进化算法、Jabir 等[3]应用混合蚁群变邻域算法对该问题进行了求解；Zhou等[4]对两级配送网络的MDVRP进行了研究，并采用多种群遗传算法进行求解；文献[5]和[6]分别利用变邻域算法和量子遗传算法对多车型MDVRP进行了求解；Mancini[7]利用大规模邻域搜索算法对多周期多车型MDVRP进行求解；文献[8]利用遗传算法对存在车辆租赁及共享且有时间窗的MDVRP进行了研究；此外，文献[9]和[10]则分别采用嵌入局部搜索的自适应邻域选择算法及粒子群算法对同时取送货MDVRP进行了深入研究.遗传算法是一种以自然选择和遗传理论为基础，利用生物进化过程中适者生存规则和种群内部染色体信息随机交换机制相结合的方式搜寻全局解的一种概率优化算法.仅利用适应性信息，以点集而非点在整个空间中做大范围并行搜索，具有很强的搜索能力.由于刚提出时的遗传算法还较为简单，现在通常称之为传统遗传算法，后来的研究人员不断探索，又提出了各种改进遗传算法.本文在传统遗传算法的基础上，针对MDVRP的特征设计了一种混合遗传算法(Hybrid Genetic Algorithm，HGA)，通过设计新型编解码方式、混合算子以及广度搜索与深度搜索平衡策略，有效地提升算法性能，旨在通过该算法以获得较高质量的满意解.

1 问题描述及数学模型

现有的区域内多配送中心配送多采用分区域独立配送模式.多个配送中心虽同属于一家企业，但一般情况下，企业会根据行政区划为每个配送中心划分一个业务范围，各配送中心间相对独立.在分区域独立配送模式下，一个客户会固定从属于某一特定配送中心，而不会根据客户的地理分布和需求特性进行调整，易导致各配送中心间任务分配不均.从理论研究的角度来看，此类求解MDVRP的方法是“先分组后路径”，即分区域规划思想，将各配送中心割裂开来.分区的结果会直接影响区内路径的规划结果，不合理的分区算法常常会导致较差的路径规划.为避免此类问题的出现，本文采用整体配送模式，引入一个与所有的实际配送中心相连且距离为0的虚拟配送中心，所有车辆均从该虚拟配送中心出发，经过实际配送中心对客户进行服务，然后再经实际配送中心返回该虚拟配送中心.

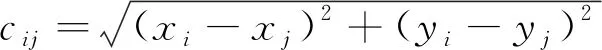
则多中心车辆路径问题的数学模型如下：

(10)

图1 编解码方式示意图Fig.1 Coding mode diagram

式(1)为最小化运输总成本；式(2)为车辆容量约束；式(3)为车辆数约束；式(4)为各节点进出平衡约束；式(5)为所有车辆均从虚拟配送中心出发并最终全部返回虚拟配送中心；式(6)为各配送中心间不能有车辆直接相连；式(7)保证任一客户由且仅由一辆车进行配送；式(8)为消除子回路约束；式(9)和(10)为决策变量属性.

2 混合遗传算法设计及实现

遗传算法一般由编解码、个体适应度评价以及遗传运算三大主要部分组成.在遗传算法中，常定义种群为所编码后的染色体集合，而个体是其相应染色体的表现型.

2.1 编解码方式

传统遗传算法的编解码方式多采用二进制编码，然而对于VRP，采用二进制编解码则可能需要额外的修复机制对产生的不可行解进行修复，从而导致问题的求解时间变长.为避免此类情况发生，现有文献对VRP多采用自然数编解码，如由1个配送中心(编号为0)、10个客户(编号为1～10)以及3辆车组成的配送网络中，编码0340278105690，解码后表示路径0-3-4-0、0-2-7-8-1-0以及0-5-6-9-0.考虑到车辆容量限制会导致车辆实际装载量不固定，进而致使所用车辆总数不固定.即在该编码方式下，染色体长度可能会因为配送方案的不同而不固定，从而导致计算效率下降.因此，本文在传统编解码方式的基础上，提出一种能够有效表达客户信息、配送中心信息以及车辆路径信息的编解码方式.

一个完整的配送网络信息由两部分组成：①编码：本文的编码采用全客户编码，这一部分记录所有客户的先后服务顺序，体现在染色体上，其长度固定(即客户数目)；②解码：为不改变编码长度，本文的解码分为两个阶段，第一阶段是对首尾客户位置进行解码，这一阶段记录每辆车第一个服务的客户以及最后一个服务的客户在染色体中的位置，解码长度与所用车辆数有关；第二阶段是路径解码，这一阶段记录每辆车所属的配送中心以及所服务的全部客户.如图1所示，现有2个配送中心(编号为1～2)、10个客户(编号为3～12)和3辆车的配送网络，全客户编码为8-3-7-12-9-5-4-10-6-11.首尾客户位置解码为[1,3]、[4,7]、[8,10]，即第1辆车从第1个客户(客户8)开始服务，服务完第3个客户(客户7)返回配送中心.同理，该染色体对应的路径解码则表示为R1：1-8-3-7-1、R2：1-12-9-5-4-1、R3：2-10-6-11-2.

本文通过将配送网络信息分开表示，在遗传操作时，只对编码长度固定的第一部分信息进行操作，遗传操作完成后，第一部分全客户编码即已完成，此时根据车辆容量约束重新为每个车辆分配客户，解码获得第二部分的首尾客户位置，再根据首尾客户位置计算出最近的配送中心，从而再解码获得最终的路径.也就是说第一部分全客户编码决定了后面的解码，只要第一部分信息是正确的，则由其产生的最终路径编码也一定是正确的，即通过此编码方式产生的个体进行扰动产生的新个体一定为原问题的可行解.且该编码方式有利于计算机实现，运算效率较高.

2.2 扰动过程

传统遗传算法的扰动算子主要包括交叉和变异，其中交叉算子模拟自然界有性繁殖，采用两个父代个体繁殖子代个体，对于整数编码的问题，简单随机交叉产生的子代个体很可能不再是原问题的可行解，故在VRP中常使用部分匹配交叉(Partially Mapped Crossover，PMX)、顺序交叉(Order Crossover，OX)等复杂交叉算子.单亲遗传的所有遗传操作均在一条染色体上完成，计算效率能够得到很大提升，但由于各个体间缺乏基因交流，易陷入“进化瓶颈”；而双亲遗传中子代则能够继承父代两个体的优良基因，遗传过程中父代基因得到充分的交流，有利于突破“进化瓶颈”，然而双亲遗传也存在一些缺陷，如计算效率较低等.针对单亲遗传与双亲遗传各自的特点，本文算法的扰动过程采用单亲遗传算子与双亲遗传算子相结合的方式.

2.2.1单亲遗传算子单亲遗传算子一般有3种操作：

(1) 插入算子(Insertion Operator).选择一个客户并插入到某个客户后面.如图2(a)所示，选择路线A上客户1，插入客户3之后的位置，形成插入后路线A′.

(2) 互换算子(Reciprocal Exchange Operator).选择两个客户并交换两个客户位置.如图2(b)所示，选择线路A上客户1与客户3，互换位置后形成路线A′.

(3) 反序算子(Inversion Operator).选择两个客户并将两客户间所夹客户进行反序.如图2(c)所示，选择线路A上客户1与客户5，将所夹客户2～4进行反序形成线路A′.

图2 单亲遗传算子示意图Fig.2 Partheno-genetic operator

图3 双亲遗传算子示意图Fig.3 Parent genetic operator

在传统双亲遗传算法中，一般随机选取两个体进行交叉，此方式保证了所有个体间基因的充分交流，但也会导致优秀基因不能拥有更多的交流，故本文在采用传统交叉方式的同时，还模拟生物界繁衍模式——首领的基因拥有更多的机会传递给下一代，在双亲遗传算子中采用全局最优个体与父代中任意个体交配的方式产生子代个体.

以文献[13]中算例为例分析各遗传算子在求解时间和质量上的差异(设置种群规模 pop_size=200，最大遗传代数M=100)，对各算子分别求解10次，求解结果如表1所示，在表1的基础上分别对求解时间和求解质量进行对比，对比结果如图4和5所示.由图可知，单亲遗传算子(算子1～4)的求解时间明显较短，而在各单亲遗传算子中，混合单亲遗传算子较单个单亲遗传算子的求解质量要高.双亲遗传算子(算子5～7)的求解时间较单亲遗传算子而言求解时间明显较长，在求解质量上，由于随机交叉算子(算子5)的目的在于种群内的基因充分交流，使得解保持多样性，而忽略了优秀个体的基因对后代解的质量的影响，致使获得解的质量最低；首领交叉算子(算子6)注重于种群中最优秀个体(首领)

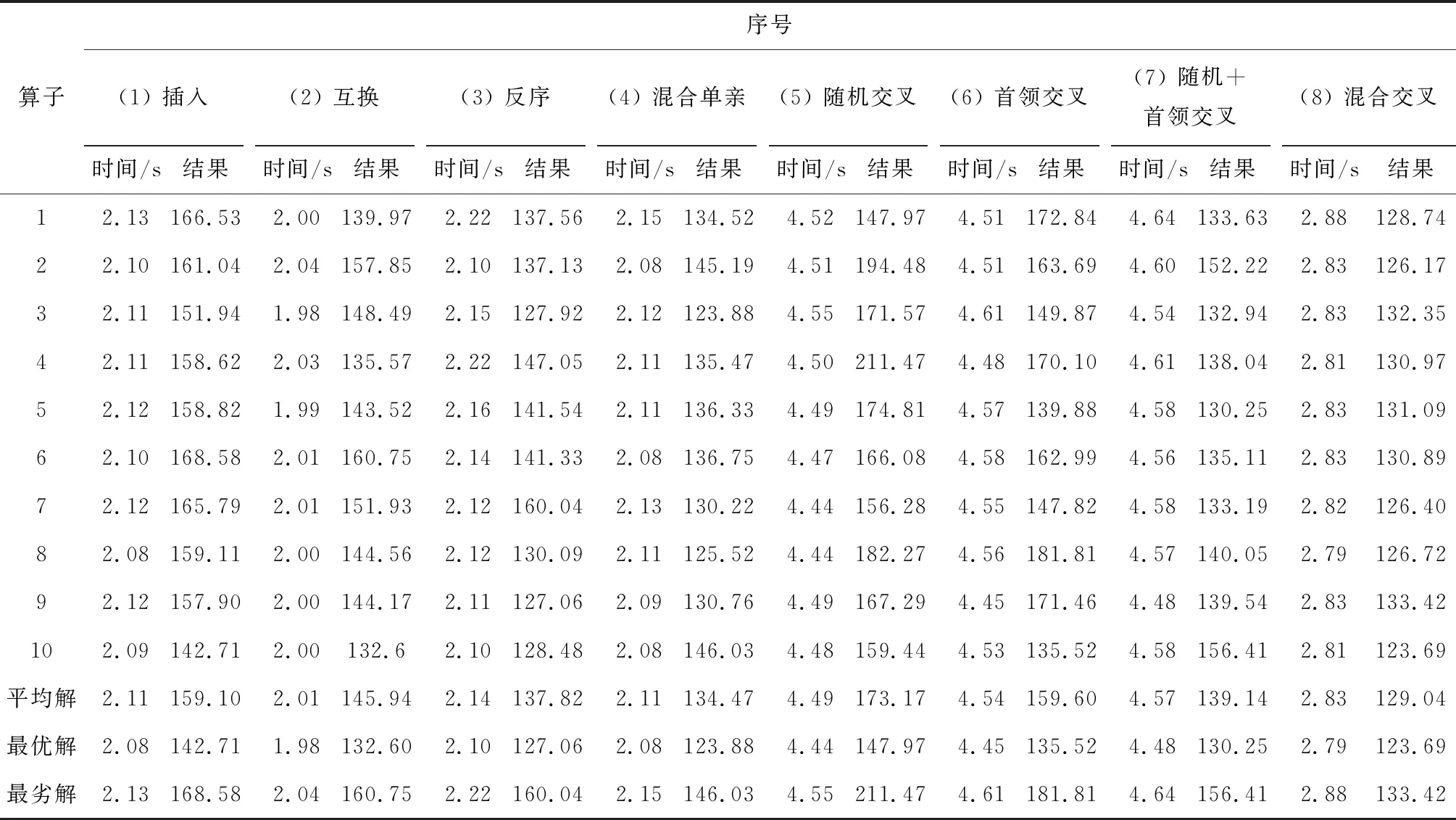
表1 各遗传算子求解结果统计表Tab.1 Results of various genetic operators

图4 各算子求解时间对比Fig.4 Efficiency comparison of operators

图5 各算子求解质量对比Fig.5 Solution quality comparison of operators

基因的遗传，故而在解的质量上有所提高；混合交叉算子(算子7)是对算子5～6的混合，综合考虑了不同双亲遗传算子中对解的质量与解的多样性的影响，求解质量进一步提高；本文算子(算子8)则综合采用了单亲遗传算子与双亲遗传算子的优势，在求解时间和求解质量取得一定的平衡，使得整体效果最佳.

2.3 选择操作

遗传算法选择操作有轮盘赌、锦标赛以及精英策略等多种方法，本文采用精英策略与轮盘赌混合选择策略.对每代种群pop_size条染色体先进行扰动操作，产生包含C_pop_size条染色体的子代种群，首先通过精英策略选择适应度值最高的αn条染色体，之后从其余的C_pop_size-αn条子代种群中采用轮盘赌策略选取(1-α)n条染色体，通过控制参数α可以调节子代种群中精英个体和非精英个体的比例，从而实现深度搜索与广度搜索的平衡.α∈[0,1]，且α的值越大，种群中精英个体越多，则算法偏向于深度搜索；反之，则偏向于广度搜索.根据pop_size大小，一般α取 0.05～0.15.

此外，在利用轮盘赌选择子代个体时，为防止较差解进入子代，本文用参数β控制C_pop_size-αn条染色体中参与轮盘赌的个体比例，平衡种群多样性与种群质量.β∈(0,1]，且β的值越大，参与轮盘赌的个体越多，种群多样性越好；反之，则参与轮盘赌的个体越少，种群中精英个体越多，种群质量越好.根据C_pop_size-αn大小，一般β取0.05～0.15.

文献[13]中3个配送中心及30个客户组成的配送网络规模适中，故以文献[13]中算例分析不同选择操作对解的影响，除选择方式不同外，所用算法其他部分完全一致，对各选择操作分别求解10次，求解结果如表2第2～4列所示，从表中可知，3种选择方式策略中，解的质量从高到低依次为本文的混合选择策略、精英+轮盘赌方式策略、轮盘赌方式策略，图6为3种选择方式策略10次求解算例的结果，由图6可知，采用轮盘赌方式策略获得的解整体质量较差，且解的波动程度较大；采用精英+轮盘赌方式策略获得的解虽然在质量上有所提升，但依然不够稳定，本文采用的选择方式策略则能获得较高质量的解，且解的稳定性较好.

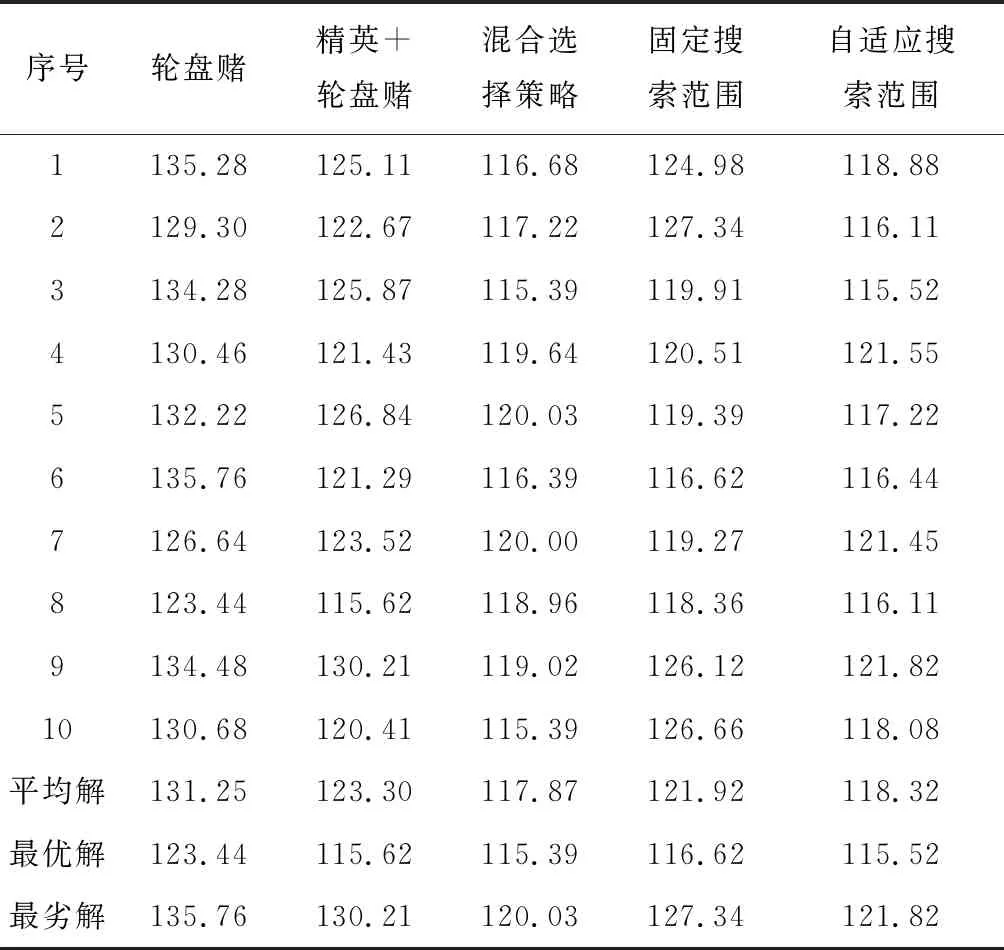
表2 不同选择策略下的求解结果Tab.2 Results under different selection strategies

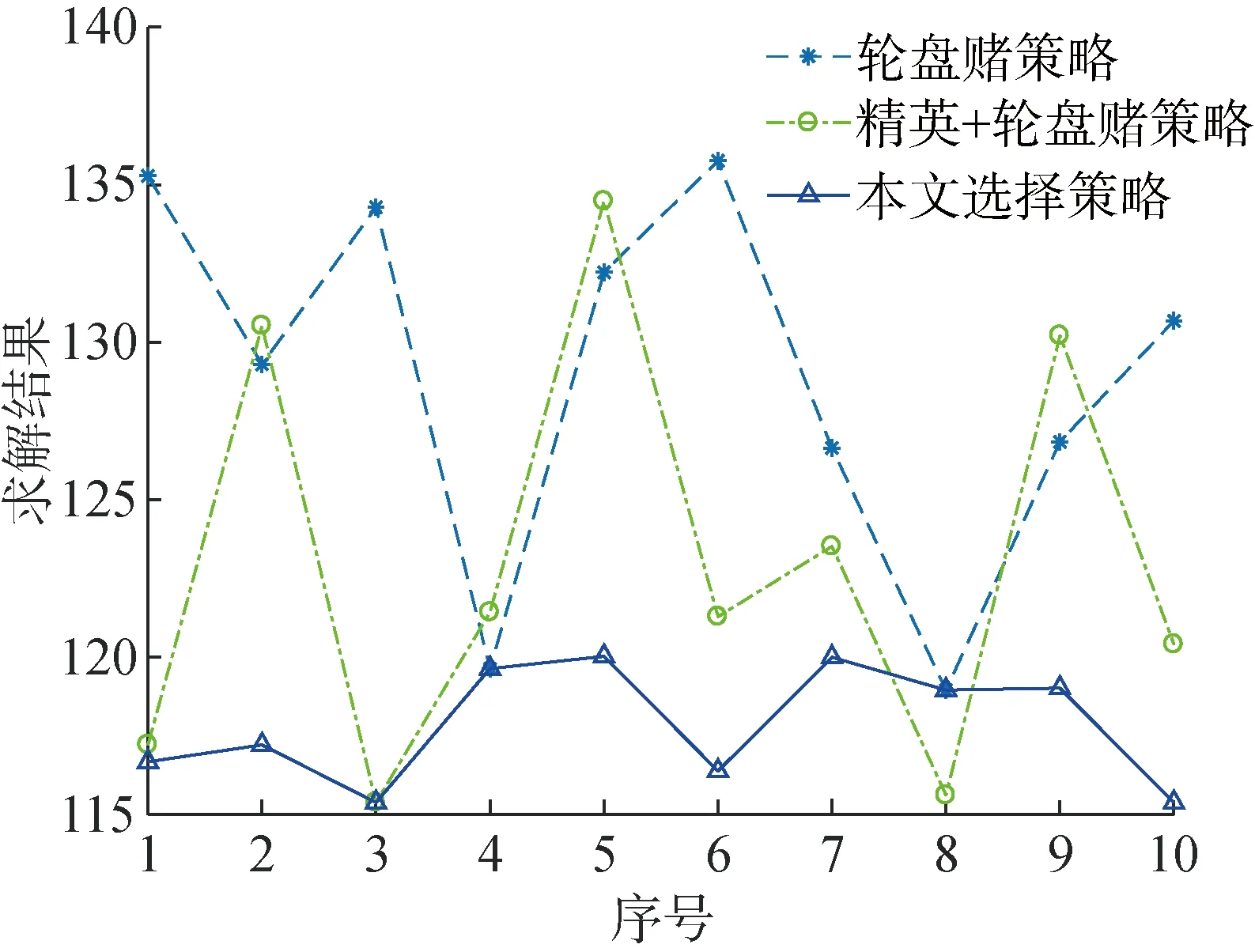
图6 不同选择策略下的求解结果对比Fig.6 Result comparison under different selection strategies

2.4 自适应搜索范围策略

由于群体在进化过程中，各阶段需要的进化压力不同.需要平衡搜索深度与搜索广度之间的关系，故本文除在选择算子中采用精英机制与轮盘赌相结合的策略以外，还构造了一种自适应搜索范围策略来进一步平衡此种关系：

(11)

式中：Ng为第g代个体的搜索范围，即第g代个体进行邻域扰动的次数；r1为最小搜索范围；r2为自适应搜索范围.

显然子代种群规模C_pop_size=Ngpop_size.图7所示为相应的示意图.

图7 自适应搜索范围策略Fig.7 Adaptive search range strategy

由图7可知，在进化初期，由于种群朝着适应度值高的方向进化速度较快，以扩大搜索广度为主，故扰动次数较少，在每个个体的附近搜索范围较小；但随着种群的进化速度越来越慢，搜索广度已不是制约进化速度的主要因素，搜索深度则对种群进化的影响越来越大，故扰动次数越来越多，在每个个体的附近搜索范围越来越大.通过对每个个体的潜在进化能力进行激发，促使其跳出局部最优解.

为分析本文所提自适应搜索范围策略的效果，仍以文献[13]中算例为例与固定搜索范围策略相对比，在对比之前，先给出以下命题及其证明：

命题采用如式(11)所示的自适应搜索范围策略进行搜索时，当最大遗传代数较大时，平均每代搜索的次数主要取决于最小搜索范围和自适应搜索范围.

证明证明过程如下：

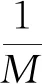
(12)

证毕

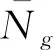
3 实验与结果分析

实验1为验证本文所提出混合遗传算法的有效性，采用文献[13]算例，以MATLAB R2012a为编译平台，在双核奔腾G2020/2.9 GHz微机上运行程序.实验数据如表3所示，实验参数设定如下：种群规模pop_size=40，最大遗传代数M=100，控制参数α=0.15、β=0.1，最小搜索范围r1=30，自适应搜索范围r2=50.

在边长为20 km的正方形区域内的配送网络中有3个配送中心和30个客户，其中每个客户的货物需求均不超过2 t，每个配送中心有4辆最大装载量为10 t的车辆，车辆单次配送的最大行驶路程均为50 km.文献[11-12]均采用先分组后路径的配送方式将多中心车辆路径问题转化为一般车辆路径问题，然后分区配送，这本质上是一种局部优化求解思想；而本文采用先路径后分组的配送方式对配送网络整体进行考虑，进行全局优化.已知该算例的目前最优解为 116.01，图8所示为本文算法求解得到的最优路径安排图(图中括号内为该客户点的需求量)，表4给出了本文的混合遗传算法对该算例进行20次重复求解结果与文献[11]中的禁忌搜索算法、文献[12]中的聚类分层算法以及文献[13]中的云量子遗传算法的对比.

由表4可以看出，本文设计的混合遗传算法求得的最优结果为 115.39，相比禁忌搜索算法求得的最优结果 177.53 提高了 35.00%，比聚类分层算法以及云量子遗传算法求得的最优结果也分别有着 6.44% 和 0.53% 的提高.通过对最优解、最劣解、平均解以及计算时间等各项性能参数的统计可以发现：本文算法与其他3种算法相比，在求解时间方面至少缩短20倍以上，求解时间降幅达 95.58%，虽然考虑到计算机硬件等因素的不同，但也是很大的提升；在算法稳定方面的提升也超过了20%.即本文算法相较于禁忌搜索算法、量子遗传算法以及云量子遗传算法，无论是在求解时间上还是在解的质量上都有着明显的改进，说明本文算法的求解时间更短、全局寻优能力更强、算法稳定性更好.

表3 客户需求信息Tab.3 Information of customer demand

图8 最优路径Fig.8 Optimal path

表4 算法性能对比分析Tab.4 Contrastive analysis of algorithm performance

注：本文算法性能提升幅度是指本文算法性能比其他3种算法中性能最好的算法性能提升幅度.

表5 MDVRP标准算例实验结果对比Tab.5 Comparison of the experimental results for MDVRP standard examples

图9给出了相应的迭代收敛图，由图9可知：对该算例约在40代左右找到最优解，说明本文算法能够在较少的遗传代数内找到问题的最优解，收敛速度快.此外，从迭代收敛图还可看出，在30代左右，

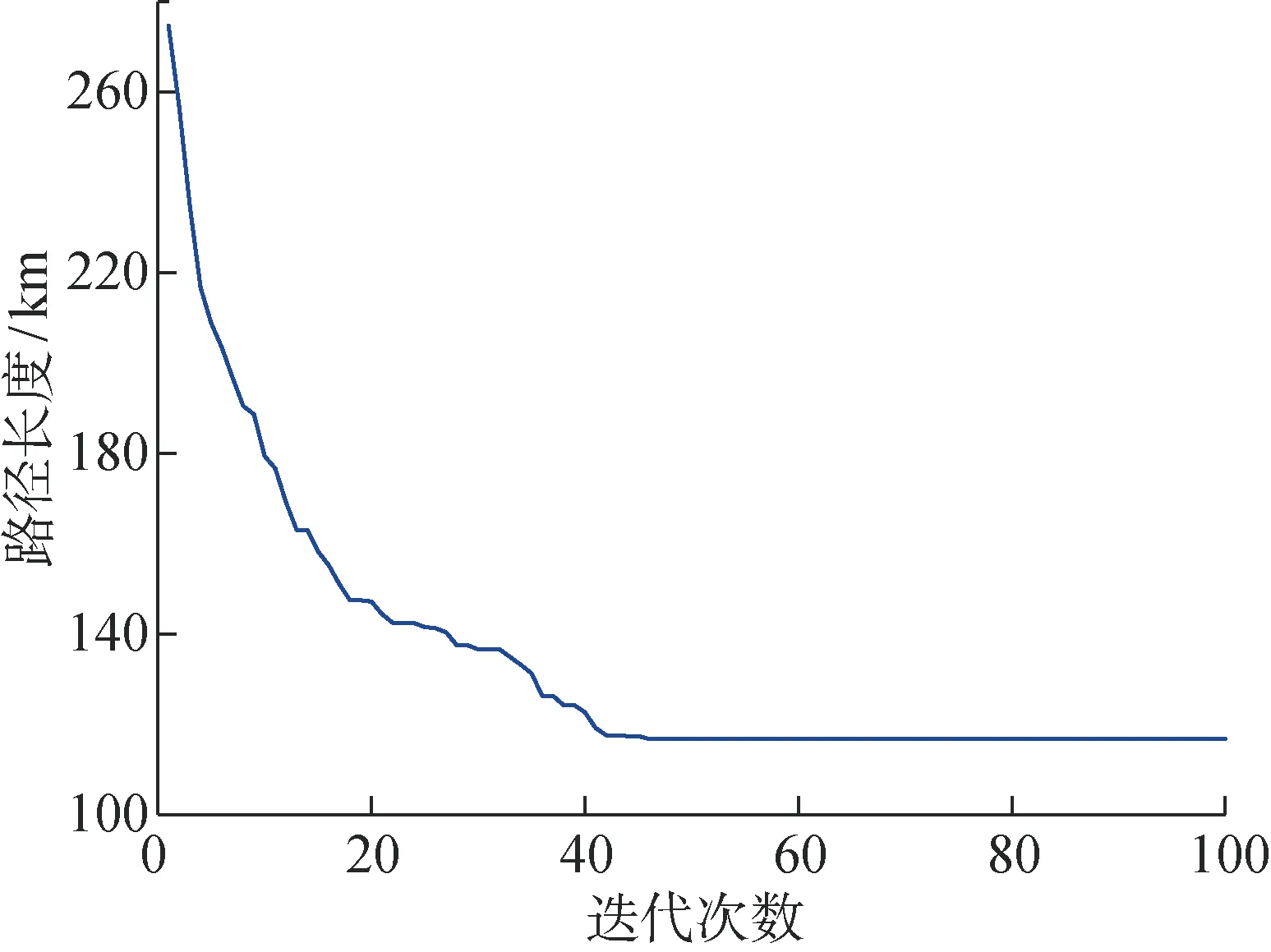
图9 迭代收敛图Fig.9 Iterative convergence graph

进化进入瓶颈，通过本文所设计的进化策略可以有效逃脱局部最优解.

实验2为了进一步测试本文所提出算法的性能，从标准算例库(来源：http:∥neo.lcc.uma.es/vrp/vrp-instances/multiple-depot-vrp-instances/)中下载MDVRP的相关数据，表5第2列给出了算例P01～P06共6个算例的相关信息，客户规模为50～100.由于客户规模不确定，故实验参数设定如下：种群规模pop_size=40，最大遗传代数M=300～1000，控制参数α=0.05～0.15、β=0.05～0.15，最小搜索范围r1=30～50，自适应搜索范围r2=70～170.

图10 标准算例最优路径图Fig.10 Optimal path of standard examples

表5第4列至结束给出了本文算法与其他5种算法对比的结果，图10所示为本文求解的最优路径图.从遗传算法改进的角度来看，本文提出的混合遗传算法明显比文献[16]中基本遗传算法解的质量要高，由此可见本文所设计的混合遗传算法是有效的，能够整体提升传统遗传算法解的质量.与其他算法相比，虽然部分解的质量并不是最好，但整体求解效果较好，平均误差较其他算法更低，且在所有6个算例中有3个算例达到了已知的最优解，其他未达到最优解的3个算例求解结果与已知最优解的误差最大也不超过2.5%，表明本文所提出的混合遗传算法属于具有一定竞争力的算法.