基于时域解析估计的多重信号分类波束形成方法
2019-09-05汪永明黄海宁
李 冰, 汪永明, 黄海宁
(1. 中国科学院信息工程研究所, 北京 100193; 2. 中国科学院声学研究所, 北京 100190;3. 中国科学院大学, 北京 100190)
宽带信号具有较强的抗干扰能力,已广泛用于声纳、雷达、地震勘探等领域.到目前为止,已有许多学者对宽带信号的抑制、检测和方位估计问题进行了深入研究并取得了显著成果,尤其是对具有高分辨能力的频域多重信号分类(MUSIC)波束形成方法的研究[1-4].具体方法:首先,通过数据分块在频域构建协方差矩阵,再通过特征分解而实现噪声子空间的求取;然后,将阵元域的数据转换为波束域的数据[5-6].与最小方差无畸变响应波束形成方法相同,由于在频域估计协方差矩阵需要对数据进行分块处理,所以MUSIC波束形成方法对数据平稳性的要求较高[7-8],且宽容性较差.主要表现在:① 当数据分块数不够大时,协方差矩阵将存在估计误差,无法稳定获得具有与目标波达方向对应的导向权向量正交的噪声子空间,且输出波束的稳定性较低,存在虚假目标和波束分裂的现象;② 当存在快速运动目标或干扰时,目标信号或干扰本身在空间上是非平稳的,难以根据多个数据块来估计协方差矩阵,从而限制了实际工程应用[7].
本文根据文献[7-8]中的时域解析思想,提出一种基于时域解析估计子空间的MUSIC波束形成(TAMUSIC)方法.其中,基于时域处理,在短时间内能够获得足够多的时间采样点,通过多个时间采样点的累积来获得良好的协方差矩阵的估计,进而获得与目标波达方向对应的导向权向量正交的噪声子空间.同时,经过采样的数值仿真及实测数据对其稳定性进行验证,以期为MUSIC波束形成方法在实际工程中的应用提供参考.
1 MUSIC波束形成方法
1.1 基本原理
MUSIC波束形成方法是在噪声(包括干扰)与信号不相关的假设下对协方差矩阵Rx(x为阵元接收数据)进行特征分解,从而得到信号特征向量Us和噪声特征向量Uv.依据噪声向量与导向权向量的正交性[4-5],所得来波方向的输出波束为
(1)

由MUSIC波束形成方法输出的波束过程可知,利用MUSIC波束形成方法时需要对Rx进行特征分解,且Rx需满足:①Rx中不含干扰与信号、信号与噪声相关的成分;②Rx需满秩.另外,由于阵元间存在相位差,所以需要导向权向量为复数,以便于在目标波达方向获得与其对应的导向权向量正交的噪声子空间.
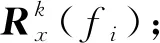
(2)


1.2 数据块个数对波达方向估计性能的影响
由于目标的快速运动而使MUSIC波束形成对目标波达方向的估计性能变差.对于频率为fi的窄带信号,第k个数据块的互谱矩阵可表示为
(3)
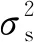
为了进一步说明目标方位对MUSIC波束形成的影响,本文通过公式表达数据块对MUSIC波束形成的影响.
由K个数据块所得MUSIC波束形成的输出波束方差σPM(θ)可近似表示为[10-11]
(4)
由式(4)可知,在线阵阵元数N一定时,数据块个数K对MUSIC波束形成的σPM(θ)的影响较大,在实际应用中一般取K≥2N,即随着数据块个数增多,MUSIC波束形成的σPM(θ)减小.
(5)

表1 不同子带频率下的可用数据块个数Tab.1 The available number of snapshots
2 基于时域解析的TAMUSIC波束形成方法
2.1 基本思想
对于时域数据,通常采用一个数据块即可获得具有信号与噪声不相关和满秩条件的协方差矩阵[9-10].若能引入复导向权向量,则可在单个数据块的条件下实现MUSIC波束形成,进而降低快速运动目标对MUSIC波束形成的影响.TAMUSIC波束形成方法的基本思路:通过Hilbert变换得到两路正交数据,将两路正交信号合为一路复数解析数据,再将复数解析数据引入复导向权向量,构造经过时延后的协方差矩阵,利用特征分解的方法求取与目标波达方向对应的导向权向量正交的噪声子空间,并利用噪声子空间自身的正交特性获得来波方向波束.也就是采用时域解析数据来实现MUSIC波束形成.
TAMUSIC波束形成方法是通过计算不同搜索角度下的延时τn而实现波束形成的.对此,可采用文献[12-13]中的方法精确估计延时,以降低延时误差对TAMUSIC波束形成的影响.
2.2 数学模型
假设N个阵元线列阵在时刻t接收的数据为
X=S+V
(6)

对式(6)进行Hilbert变换,可得

(7)


图1 Hilbert变换示意图Fig.1 Schematic diagram of Hilbert transformation

(8)


(9)
ω为角频率.
依据Hilbert变换的结果,采用阵列接收数据构造的时域复解析数据为[7]
(10)
式中:|X|和φ0分别为Y的幅度和相位;YS为变换后信号含有量;YV为变换后噪声含有量.
结合式(9)对式(10)进行FFT变换,再经过 Hilbert 变换,所构造的时域复解析数据Y与实数据X在频域的对应关系为

(11)
可见,经Hilbert变换后的时域复解析数据是将实数据经FFT变换后的正频率数据放大 2 倍,负频率数据置 0,所以采用Hilbert变换获得的时域复解析数据并未改变各阵元之间接收信号的相对时延差.

(12)


(13)


(14)

(15)

当搜索角θ对准目标波达方向时,由式(12)所得声压输出为
(16)
式中:s为单阵元的期望信号;real(·)表示取实部函数.
与频域MUSIC波束形成方法相比,基于时域解析的TAMUSIC波束形成方法所需数据块个数较少.在数据长度满足式(15)的情况下,只需单个数据块即可得到与目标波达方向对应的导向权向量正交的噪声子空间.
由于引入时域解析数据,TAMUSIC波束形成方法放宽了对数据块个数的条件限制,且不需进行子带分解,从而大幅降低了计算量,并拓宽了适用范围.但是,在一个搜索角度上,TAMUSIC波束形成方法只有一组子空间,而频域MUSIC波束形成方法相对于每个子带均有一组子空间,其子空间组数为TAMUSIC波束形成子空间组数的数倍.因此,需要数值仿真和实测数据进一步对比两种方法的噪声抑制及抗干扰能力.
3 数据处理与分析
3.1 数值仿真分析
本文在3种情况下对两种波束形成方法的输出波束响应、目标检测和方位估计性能进行数值仿真分析.

图2 TAMUSIC与MUSIC波束形成方法输出的波束Fig.2 Output beams of TAMUSIC and MUSIC beam-forming methods
3.1.1单目标情况 其仿真条件:采用16阵元的等间隔线列阵,间距为半波长,噪声为空间加性白噪声,目标信号与背景噪声的谱级比为20 dB,目标方位相对阵列端射方向(0°)为90°.一次处理的数据长度为2×104个采样点,由单个数据块(2×104个采样点)形成TAMUSIC波束,由100个数据块(单个数据块长度200)形成频域MUSIC波束.图2所示为两种波束形成方法输出的波束.可见,当目标方位稳定时,两种波束形成方法对窄带目标信号的波束响应基本相同.
3.1.2双目标情况 其仿真条件:目标信号为两个相同强度的宽带信号源,目标信号的带宽均为 600~900 Hz,目标波达方向分别为85° 和90°,频域MUSIC波束形成方法处理数据所分子带个数为300,阵列条件、信号谱级比、两种波束形成方法所用数据块个数与单目标情况下的相同.图3所示为双目标情况下两种波束形成方法的输出波束.由图3可以看出,当目标方位不稳定时,虽然仿真中频域 MUSIC 波束形成方法的子空间个数为TAMUSIC波束形成方法的子空间个数的300倍,但基于时域解析的TAMUSIC波束形成方法输出的波束优于频域MUSIC波束形成方法.

图3 双目标情况下TAMUSIC与MUSIC波束形成方法输出的波束Fig.3 Output beams of TAMUSIC and MUSIC beam forming for double targets

图4 MUSIC和TAMUSIC波束形成方法输出的方位历程图Fig.4 Bearing time records of MUSIC and TAMUSIC beam-forming

图5 TAMUSIC和MUSIC波束形成方法输出的波束Fig.5 Output beams of TAMUSIC and MUSIC as target signal azimuth fast changing t=50 s)


图6 MUSIC和TAMUSIC波束形成方法输出的方位历程图Fig.6 Bearing time records of MUSIC and TAMUSIC beam-forming methods
由以上仿真结果可见:在一般情况下,两种波束形成方法的输出波束响应基本相同;在目标相对线阵方位变化时,TAMUSIC波束形成方法可以改善频域MUSIC波束形成方法对目标波达方向的估计性能,降低数据块个数对输出波束的影响;目标方位变化越快, 频域MUSIC波束形成方法对目标波达方向的估计性能越差,而本文所提TAMUSIC波束形成方法对目标波达方向的估计性能未发生变化,对目标方位变化的宽容性较好.
3.2 海试数据处理

图7 海试数据下MUSIC和TAMUSIC波束形成方法输出的方位历程图Fig.7 Bearing time records of MUSIC and TAMUSIC beam-forming methods for sea trial data
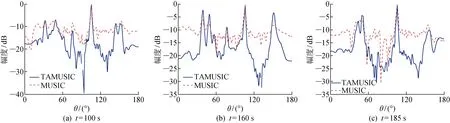
图8 不同时刻AMUSIC与MUSIC波束形成方法输出的波束Fig.8 Output beams of TAMUSIC and MUSIC beam-forming methods under different time
为进一步验证TAMUSIC波束形成方法的目标检测和方位估计性能,本文分别利用两种波束形成方法对2012年4月的拖线阵试验数据进行分析.试验中,拖线阵为均匀分布的32阵元等间隔水平直线阵,阵元间距为d=8 m;处理数据的时间长度T0=200 s,该时间段内的目标方位(θ)分别为30°、50°、55°、80°、105°、145° 和150°,105° 附近为一个强目标.线阵拾取各阵元采集数据所用采样率为20 kHz,估计频域MUSIC波束形成方法的协方差矩阵时,一次处理的数据长度为4×104个采样点.具体处理过程:首先,将数据分块,每块数据为 1 024 个,记为一个数据块数据长度,数据段之间重叠512个,数据块个数为76,进行FFT变换后选取60~300 Hz频段,对每个频率点分别进行协方差估计.而TAMUSIC波束形成方法通过256阶带通滤波器选取60~300 Hz频段,采用一个数据块(4×104个采样点)进行分析处理.图7示出了两种波束形成方法所得方位历程图,图8示出了不同时刻两种波束形成方法输出的波束.由图7可以看出:采用TAMUSIC波束形成方法所得方位历程图中目标航迹清晰,目标方位明晰可辨;而采用频域MUSIC波束形成方法在0~120 s时间段内无法检测140° 附近的快速运动目标,在120~180 s时间段内无法检测50°~60° 附近的快速运动目标,在整个时间段内对20°~40° 运动目标的检测效果差于TAMUSIC波束形成方法,无目标处的输出波束谱级较大.其原因在于:目标信号和背景噪声的平稳时间较短,不能满足频域MUSIC波束形成方法对多个数据块的时间要求,从而产生了失配现象.由图8可以看出,与频域MUSIC波束形成方法相比,采用TAMUSIC波束形成方法所得空间谱的主副瓣比高出3 dB,表明TAMUSIC波束形成方法比频域MUSIC波束形成方法的旁瓣级最少降低3 dB.
另外,由图7还可见,在160~200 s时间段内,与频域MUSIC波束形成方法相比,TAMUSIC波束形成方法能够更好地检测45° 附近的双目标.另外,对比图8(c)中的波束可知,与频域MUSIC波束形成方法相比,TAMUSIC波束形成方法能够更好地分辨45° 附近的两个目标,表明TAMUSIC波束形成方法具有更强的方位分辨能力.
在该段数据处理中,采用两种波束形成方法,在酷睿双核i5-3337U、单核运算能力为 1.8 GHz的计算机上利用MATLAB 2008b的CPU TIME软件进行计算,所得到的TAMUSIC波束形成方法与频域MUSIC波束形成方法完成一次波束输出的计算时间分别为 22.3,13.5 s.计算所用采样率较高,TAMUSIC 波束形成方法未作精确时延处理.由于TAMUSIC波束形成方法只对一次快拍数据进行处理,并未进行频带分解,故其计算时间小于频域 MUSIC 波束形成方法.
4 结语
本文提出一种基于时域解析估计子空间的TAMUSIC波束形成方法.在构造时域解析数据的基础上,在阵列的时域解析数据中引入复导向权向量,构造经时延后的协方差矩阵,利用特征分解方法求取具有正交性的噪声子空间,利用噪声子空间自身的正交特性获得来波方向波束,并通过数值仿真和实测数据处理对所提方法进行验证.结果表明,在单个数据块的条件下,TAMUSIC波束形成方法可以获得足够多的时间采样点数,并通过多个时间采样点的累积获得良好的协方差矩阵估计,进而得到具有正交特性的噪声子空间.数值仿真及实测数据处理结果表明:与频域MUSIC波束形成方法相比,TAMUSIC波束形成方法对于宽带信号的检测和方位估计的稳定性更高;在不存在目标方位快速变化的情况下,两种波束形成方法的波束响应基本相同,但TAMUSIC波束形成方法的运算时间较短;在目标方位快速变化情况下, TAMUSIC波束形成方法能够稳定获取噪声子空间和来波方向波束,使波束旁瓣级最少降低3 dB,精确检测运动目标,且未出现虚假目标和波束分裂的现象,从而提高了MUSIC波束形成方法在工程应用中的稳定性.
