实施问题有效驱动 提高复习课有效性
——以一道典型问题的教学为例谈逻辑推理素养的培养
2019-09-05邮编242400邮编242400
(邮编:242400)(邮编:242400)
安徽省南陵县教研室 安徽省南陵县城东实验学校
复习课作为课堂教学的重要课型之一,对提高学生的学习能力起着不可替代的作用.复习课由于涉及的知识信息量大,对学生数学能力的培养是很好的契机,发挥着不可替代的重要作用.怎样在课堂教学中提高学生的数学核心素养呢?这是我们面临的一个现实问题,在省级课题的研究中,我们总结出一种行之有效的方法,即以问题为驱动,以知识的生长点为纽带,通过对问题进行适度变式,深化了知识,培养了学生的学习方法,对提升学生的数学核心素养起到很好的效果.
逻辑推理能力是初中数学的核心素养之一,《义务教育数学课程标准(2011版)》(以下简称课标)指出“对现实空间及图形有较丰富的认识,具有初步的空间观念、几何直观和逻辑思维能力……逻辑推理能力的发展应贯穿在整个数学学习过程中.”所以数学逻辑推理能力的培养是数学教学的重要任务.在复习课上,我们坚持选择恰当的素材,对相关知识适度整合和实施有效的驱动,在发展基础知识的同时兼顾发展能力,在注重数学活动的同时培养学生的数学素养.下面是我们实践研究中的两节初中几何“三角形”复习课:

图1
原题如图1,△ABC是等边三角形,D、E分别是AC、BC边上的点,且AD=CE,连接BD、AE相交于点F.求∠BFE的度数.
这是八年级学习时的一道典型的练习题,条件简单,结论一般,大多数学生耳熟能详.复习课上如果仅仅停留在对原题的讨论上,不能激发大部分学生学习兴趣,更谈不上培养学生的逻辑推理能力,所以我们以此题作为知识的生长点,着眼于其蕴含的丰富内容,通过对这些内容的挖掘,激发学生的求知欲,取得了很好的效果.
1 在原题的基础上增加条件,实现对全等三角形的复习
原题形式简单,通过添加相应的条件,使原题的知识内涵更丰富,有利于培养学生的逻辑思维能力.

图2
例1 如图2,已知△ABC是等边三角形,D、E分别是AB、BC上的点,且BD=CE,AE、CD交于点F.
(1)求证:△ACE≌△CBD;
(2)过A作AG⊥CD于G,求证:AF=2FG;

图3
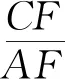
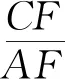

图4
解(1)、(2)略;
(3)如图4,过A作AG⊥DF于G,因为△ACE≌△CBD,所以∠CAE=∠BCD.
因为∠ACB=∠CAB=60°,所以∠ACB-∠BCD=∠CAB-∠CAE.
即∠ACG=∠BAF.
又因为∠AGC=∠AFB,AC=AB,所以△ACG≌△BAF.
所以CG=AF=2FG,因此CF=FG.

全等三角形作为初中数学的核心知识,如何添加辅助线是证明两个三角形全等的关键环节,常见的辅助线添加的方法有截长补短、中线延长和旋转等,为了实施对全等三角形的复习,在完成例1后,再次添加条件,得到变式:

图5
变式一:如图5,在(3)的条件下,点H在BC上且∠BFH=30°,求证:AH⊥BH.
变式一依然是以原题为依托,但改变过去以旋转为已知,进行三角形全等的证明,据此研究线段的和、差、倍、分关系.变式的本质是旋转,即把△ACF绕点A逆时针旋转60°得到△BCM,这样对学生思维程度的要求更高,能更有效地激发学生思维的深度和广度,经过一段时间的思考、讨论、交流,学生获得下面的解法:

图6
如图6,在AF上取M使CF=FM,连MC,延长FH交MB于N,
因为∠AFC=120°,所以△CFM为等边三角形.
所以CM=CF,
∠BAC=∠FCM=60°.
所以∠BCA-∠BCD=∠FCM-∠BCD,即∠ACF=∠BCM.
又因为AB=AC,△ACF≌△BCM.所以∠BMC=120°.
又△CFM为等边三角形,所以∠CMA=∠BMF=60°.
因为∠AFB=90°,所以∠MFB=90°,∠NFB=30°.
因为∠HFB=30°,所以∠MFN=∠FMN=60°.
即△FMN为等边三角形,且FN=NB,所以NB=FN=FM=CF.
故△CFH≌△BHN,即CH=BH,所以AH⊥BC.
2 把问题的视角转到相似三角形,实现对相似三角形的复习
相似三角形作为初中数学的重要知识,在证明线段相等、角相等、线段的平行、垂直关系,在计算线段的比值、图形的周长、面积等方面有着广泛的应用.这些问题的解决,对培养学生的逻辑思维能力有着重要的作用.

图7
例2 如图7,△ABC是等边三角形,D、E分别是AC、BC边上的点,且AD=CE,连接BD、AE相交于点F.



图8

证法1 (备课预设)如图8,延长FE至G,使FG=FB,连接GB、GC.
易知∠BFG=60° ,所以△BFG为等边三角形.
所以BF=BG,
∠FBG=∠FGB=60°.
易证△ABF≌△CBG.所以∠BFA=∠BGC=120°,∠FGC=60°.


证法2 (学生解法)易知△ABD≌△CAE.所以BD=AE,∠DAF=∠ABD.

①

②


例2把全等和相似巧妙地结合起来,提示学生在全等时不忘相似,在相似时不忘全等,一箭双雕!
为了强化相似在解题中作用,有效地对相似三角形的判定和性质进行复习,同时强化学生三角形相似的意识,在解完例2后,对原题的条件进行逆向思考,提出下面的变式:

图9



图10
简解如图10,作DK∥BC,交AE于K.易证△ABE≌△BCD.所以BE=CD,CE=AD.
因为BM=DM,∠DMK=∠BME,∠KDM=∠EBM,所以△MBE≌△MDK.

为了对接安徽中考题第14题,继续对原题条件进行改造,变成一道两解填空题,提升学生逻辑推理能力的深度与广度.

图11
例3 如图11,等边△ABC的边长为6,点D在AC上且DC=2,点E在BC上,连接AE交BD于点F,且∠AFD=60°,若点M是射线BC上一点,当以B、D、M为点的三角形与△ABF相似时,则BM的长为______.
作为压轴填空题,此类问题一般有一定的难度,但这恰好可以训练学生思维的严谨性和分类讨论的意识,为什么要分类以及怎样分类是学生学习的难点.此题当点M在线段BC上时,大多数学生能够求出BM的值,当点M在线段BC的延长线上时,问题怎样转化是本题的难点所在,教学中也发现学生出现了多种解法,而且解法新颖.
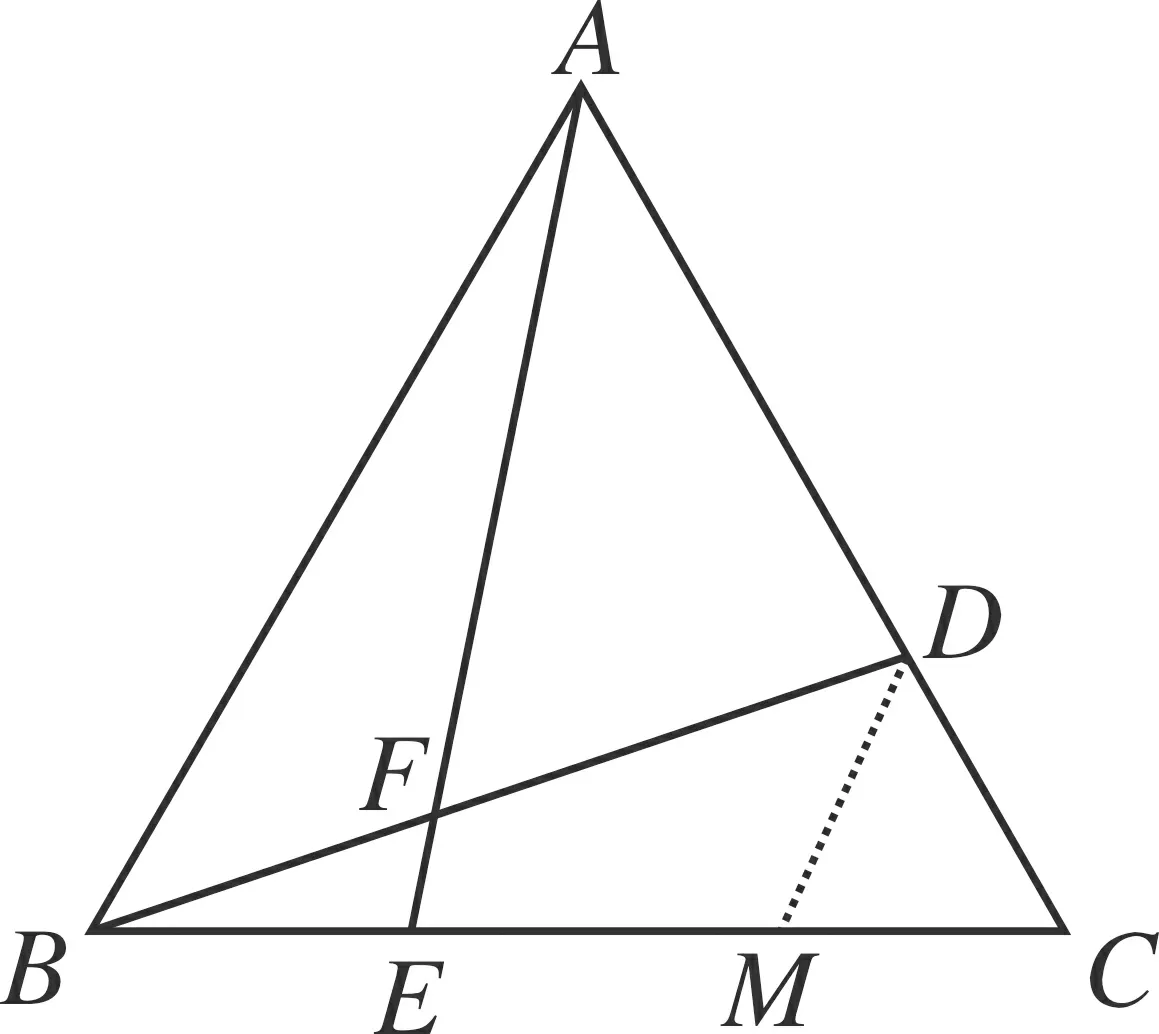
图12
简解如图12,当点M在线段BC上,∠BMD=120°时,△ABF∽△BMD.
此时△CDM为等边三角形,所以CM=CD=2,故BM=BC-CM=6-2=4.
当点M在线段BC的延长线上,∠BDM=120°时,△ABF∽△BDM.

图13
解法1 (备课预设)如图13,设CM=x,因为∠DCB=60°,∠BDM=120°,
所以∠DBM+∠M=∠CDM+∠M=60°.所以∠DBM=∠CDM.
又因为∠DMC=∠BMD,所以△BMD∽△DMC.


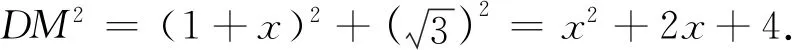
所以x(x+6)=x2+2x+4.解得x=1.故BM=x+6=7.
这个预设是执教者精心设计的,一度认为此法具有挑战性而沾沾自喜,当教师把这个答案用PPT呈现给学生时,数学课代表怯怯地说:“老师,我直接证明△ABF∽△BDM也能求出BM的长”.课后我们和老师的交流中得知,直接求解教师在备课时也思考过,考虑到过程相对比较复杂,就没有深入下去,学生的这一提出,使他感到很诧异.在课堂上,老师把这位学生的解法投影到实物展台上,供同学交流:

图14




教师对数学课代表的解法,向学生谈了自己的想法:这种解法其实我在备课时也考虑到了,但估计运算量比较大,所以我就放弃了,现在数学课代表这种最直接(最直接的往往体现的是学生最原本的认知思维)的解法深深打动了我,请大家不吝啬你的掌声,给他鼓鼓掌!
话音未落,另一个同学举手,老师示意他讲下去,他说“老师,我的方法很简单,也求出了BM=7”,该生的发言使同学们觉得很兴奋,于是叫他把过程展示如下:
如图14,在线段BC上作∠BGD=120°,∠BDM=120°,所以∠DBG=∠CDM.故△BDG∽△DMC.

例3是一道三角形综合题,借助此题复习等边三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,体会用分类讨论的思想思考问题,体验添加辅助线构造全等三角形或相似三角形解决问题的过程.课标指出“数学教学活动应激发学生兴趣,调动学生积极性,引发学生的数学思考,鼓励学生的创造性思维;要注重培养学生良好的数学学习习惯,使学生掌握恰当的数学学习方法.”此题以问题为驱动,充分调动学生学习的主动性和积极性,让学生深入思考,提高他们的逻辑思维能力,使学生的数学核心素养的培养落到实处.
在例3的基础上,顺势而为,将点D、E在AC、BC上拓展到在直线AC、BC上,并把图形相似转化为角相等,有下面的变式:
变式三在例3的条件下,点D在直线AC上,点E在直线BC上,且∠BAE=∠CBD,当BD=1时,则BE的长为___________.
为了使学生有更多的时间思考和解决此题,没有在课堂上讨论,作为作业让学生思考,第二天在课堂上点评. 变式三是例3的延伸与拓展,由于点D在直线AC上,点E在直线BC上,所以变式三有四种情况,情况更复杂,对思维的严密性要求更高,但能巩固学生对全等和相似的复习效果,强化分类讨论的思想方法.
3 在原题的基础上求线段(线段和)的最值,实现对几何最值的复习
最值问题是学生学习几何的难点,解决此类问题的基本定理有:两点之间线段最短和垂线段最短等,基本题型有将军饮马、定弦定角和运用阿波罗尼斯圆等,为了让学生掌握数学的思维方法,改变过去的所谓“题型”教学,教师对原题继续变式探究:
借助几何画板的动态演示发现,随着点D和点E的运动,点P也在运动,但点P始终在以AB为弦圆周角为120°的圆上运动,在运动过程中,CP存在最小值,于是提出下面的问题:

图15

此题在原题的条件下,将问题转化到求CP的最小值,由已知可得∠APB=120°,故点P始终在以AB为弦圆周角为120°的圆上运动,当点P经过圆心时CP最小.其模型是定弦定角求最值.

图16
解易知△ABD≌△BCE,有∠APE=60°,
从而∠APB=120°,所以∠AOB=120°.

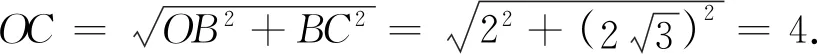
当O、P、C三点共线时PC的值最小,最小值为4-2=2.
在求得CP的最小值后,最直接的想法就是△PAB周长的变化规律,通过几何画板的反复演示,猜想△PAB的周长有最大值,最大值在哪里取得,是多少,难以发现,于是启发学生能否运用代数方法去寻求其最大值.在师生的互动下,探究如下:

图17





在代数探究的前提下,提出:
变式四在例4的条件下,求△PAB的周长的最大值.

解在△ABC外作等边△ABK,连接PK,取PH=PB.
由已知易得∠APB=120°,因为∠AKB=60°,所以∠AKB+∠APB=180°.
所以A、K、B、P四点共圆.所以∠BPH=∠KAB=60°.
因为PH=PB,所以△PBH是等边三角形.
所以∠KBA=∠HBP,BH=BP.所以∠KBH=∠ABP.
因为BK=BA,所以△KBH≌△ABP.所以HK=AP.
所以PA+PB=KH+PH=PK,所以PK的值最大时,△APB的周长最大,
所以当PK是△ABK外接圆的直径时,PK的值最大,最大值为4.
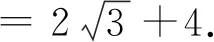
△PAB的周长最大值的取得是建立在代数探究、几何证明的基础上的,具有相当大的难度,仍然在学生的“最近发展区”,属于“跳一跳”的问题,在解决完例4和变式四后我们还需要思考对于正方形是否还有类似的结论,对于其他正多边形是否也有类似结论,如何探究,请感兴趣的同学课后思考.
以上两个课时的复习课,以问题为驱动,在学生最近发展区对有关数学问题进行变式,激发学生深入思考,促进了学生思考的深度和广度,使课堂成为安静的“热闹”,培养了学生的逻辑思维能力,提高了学生的数学核心素养,有效地提高了复习课教学的有效性.
