基于GPS的水下可见光通信系统精确对准方案设计*
2019-09-04刘雨享张亚中李玉箫农汉琦
刘雨享,张亚中,李玉箫,农汉琦
(南京邮电大学,江苏 南京 210023)
0 引 言
海洋占地巨大,含有丰富的生物资源。但是海洋的探测与信息传送也是人类研究相对薄弱的部分。水下无限通信的方式主要包括水下电磁波通信、水声通信、无线蓝绿光通信等[1]。水下无线光通信是一门新兴技术,其优越的传输性能对于海洋探索和信息采集具有重要的应用价值。尽管水下无线蓝绿光通信传输距离较短(<500 m),但其传输速率、传输带宽,传输业务,抗干扰能力,设备成本,功耗都体现出巨大的优势[2-4]。有相关研究工作表明,400 纳米波段的蓝光在海水中衰减最小,这使得利用蓝光LED进行水下高速无线光通信成为可能[2,4]。
目前的水下可见光通信技术还不太成熟,经常会受到波浪和水下生物的影响而导致收发端不对齐,接收机与发射机的轴向对准的偏差越大,收到的光功率越小,而且有关研究表明即使是小角度的偏移,对接收光功率的影响依然较大[1]。然而目前水下可见光通信收发端对齐的研究较少,与此比较相似的问题有,在卫星的通信系统中,对严格对齐的要求很高,包括硬件的永磁发动机,扫描技术,对准时间等各个方面都有严格要求[5]。
GPS定位技术也是依靠卫星完成定位的。当代GPS技术已经较为成熟,各种基于GPS的应用越来越多,GPS定位误差也不断减小[6-7],本文提出一种新的完整的水下可见光通信系统,利用GPS水上浮标定位,介绍了一种由粗瞄到细瞄逐步精确的实用性较强的水下通信系统的定位流程,并介绍了一种以最短的时间和最大的成功扫描概率为目标函数的最佳扫描步长的确定方法。运用蒙特卡洛的计算机仿真结果初步显示,得到的最佳步长与我们生活中的实际要求相符。
1 GPS水上浮标定位原理
自主水下定位系统由水上设备和水下设备两组单元构成,主要包括水下信息接收单元,四个GPS浮标,数据处理模块。如图1所示,水上设备单元的主要功能是通过接收GPS信号定位浮标。水下设备单元主要用于接收水上设备单元定位信号和处理数据。

图1 水下设备定位系统
采用水声定位球体模型。考虑到借助GPS,浮标之间可以容易的实现高精度的时间同步,本文采用双曲面交叉法,通过水面上的四个已知位置的浮标,实现水下设备的定位。图1显示了水下定位的几何模型,其中Fi表示第i个GPS的位置,D是水下航行器。
由于水下设备可能和水上浮标之间存在钟差,会带来较大定位误差,我们将水下设备的时钟时间与水上浮标时钟时间之间存在的时间同步误差作为一个待定参数。通过测量4个水上浮标至水下设备的距离数据,可得到以下四个方程式:

上述四个方程式(x,y,z)中为待测点坐标,其中di(i=1,2,3,4)分别为卫星i到接收机之间的距离,Vti分别为卫星i的信号到达接收机所经历的时间,Vt0为接收机的钟差为未知参数,xi,yi,zi为卫星i在t时刻的空间直角坐标,c为光速。由以上四个方程即可解算出待测点的坐标x,y,z和水下设备与浮标之间的钟差Vt0,实现水下设备的定位。
2 ATP(Acquirement,Pointing and Tracking)系统设计
由GPS水上浮标定位,可以得到发送接收机的位置坐标。GPS的定位误差在米级范围,设误差为a。下面介绍一种基于蒙特卡洛的扫描算法,实现粗瞄到细瞄的逐步定位。
假设水上浮标GPS定位系统给出的接受平面的位置坐标为(x0,y0,z0),那就意味着在接受平面的轴心可能在以点(x0,y0,z0)为球心,半径为a的球内任一点。设激光光束的最大可探测直径为ds,接收终端可探测直径为dv,不确定区域的直径为du,则du=2a。根据前面的叙述,我们通过转向系统使发射机的发射方向与接收平面垂直,接收机的位置可以在球内的任意位置,如图2所示。
扫描方案分两步:初步定位和精确对准。
step 1:初步定位。发射机在GPS的定位后的误差范围内扫描,当光通信系统的发射光束直径d,通信距离L,接受光强等于阈值确定的临界直径ds,接收终端可探测直径dv,不确定区域的直径du确定之后,发射机需要扫描的总范围就确定了。

图2 发射接收系统
根据前人的研究仿真,假设发射系统为3 mm光束,传输距离为50 m,接收板为0.25 m*0.25 m的正方形,当发射机与接收板的轴心偏角为10度时,接收光强衰减在-42 dB[1]。考虑到不同接收机的性能不同,对探测到的光强灵敏度不同,我们定义一个接收板能探测出的光强度的最小值,即RSS阈值。当接收到的光强强度大于这个阈值的时候,接收板就能检测到发射机发射的信号,然后给发射机做出反馈。这就完成了初步定位的过程。
初步定位的误差大小由阈值的大小确定,假设接收板接收到的光强强度正好等于阈值大小时,发射机与接收板的夹角为θ0,那么发射机对接手板的定位误差一定小于或等于θ0。
step 2:初步定位后,发射机在θ0范围内进行更精准的扫描,或者说微调,找到一个使接收机接收到的光强最大的角度,此时两者轴心之差应达到最小,即为精确定位。
2.1 光强
在光通信系统中所采用的激光多为高斯光束,则其归一化基模形式可表示为:

式中,R(z)为光束的等相位面曲率半径,fn为共交参数。
由式(2)可知在曲率半径内的横截面光强分布按照高斯函数衰减,则两轴偏差可视为服从高斯分布,则:

式中,θx为两轴指向偏差,σx为两轴均方差,f(θx)为概率密度函数。
2.2 扫描系统优化
接收板的光强由发射机功率,传输距离,海水的传输信道,杂质,噪声等共同决定,但是为了简化分析,我们假设接收板可以接收到理论上照射到的最大光强,取接收板所在的横截平面分析。
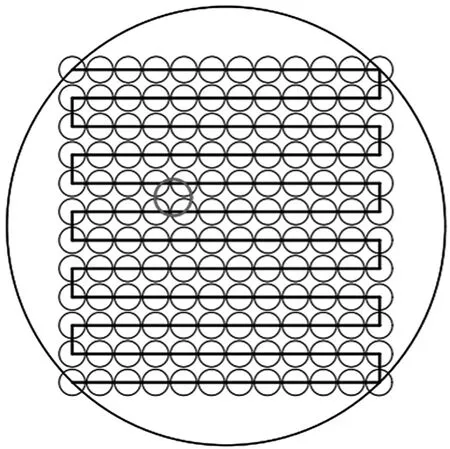
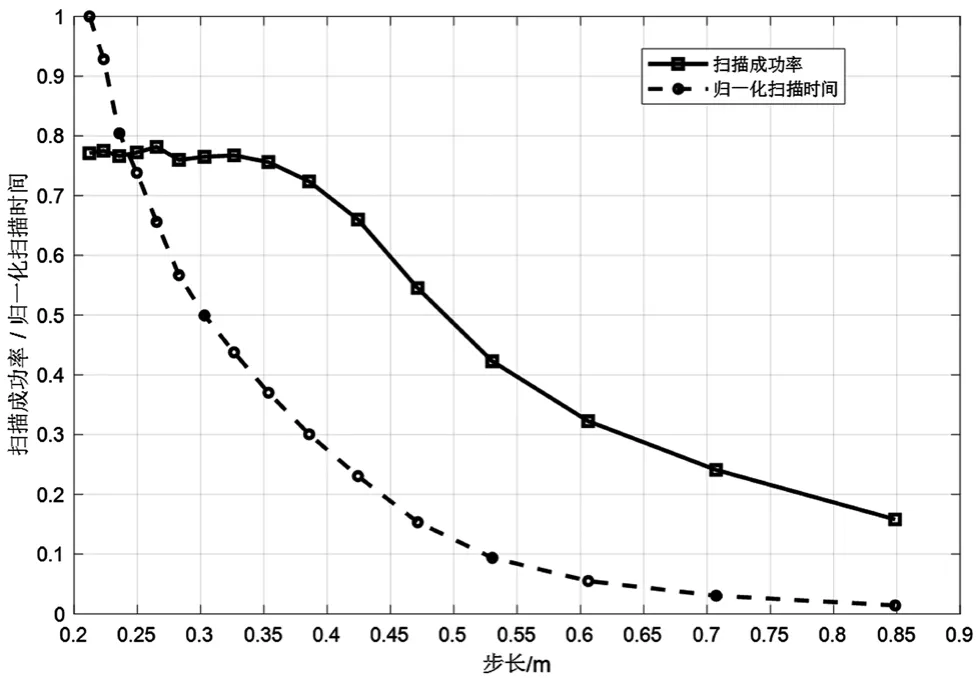
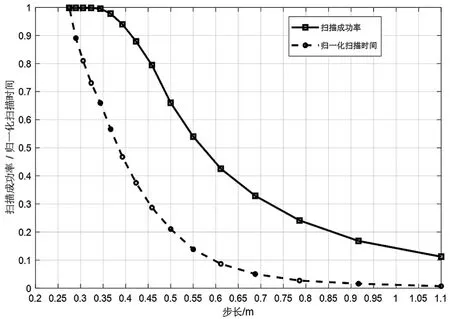
阈值的确定:假设发射光束的散射角为θs,通信距离L,那么激光光束的最大可探测直径ds=2Ltanθs。根据前面的讨论,接收板接收到的光强呈现高斯分布,这里我们假设接收板ds之外接收到的光强小到可以忽略不计。那么当接受平面为一个圆时,光强RSS可以用接受平面的圆dv与光束投影的圆ds圆心的距离l来衡量,如图3所示。通常为了使发射激光的能量充分利用,一般有ds 图3 RSS阈值示意图 我们假设接收板在半径为du的圆内出现的概率服从均匀分布,假设接收板为直径为dv的圆,扫描轨迹的可行方案可以分为螺旋式扫描和分层扫描,但是当GPS的分布概率为均匀分布时,两种方案相差无几,但是扫描面积对算法的收敛速度影响也较大。 步长确定:初步定位的关键在于步长的确定。若步长偏大,在du范围内扫描一圈之后可能扫描不到,无法初步确定其位置,从而导致总体定位的时间过长;若步长偏小,可能初步定位就扫描的很精确,但是平均定位的总时间也较长。我们按照数据样本对两个指标进行加权,得到一个综合评价函数,进而找到一个总得分最高的最佳步长。 我们假设通信系统的光源输出的光束宽度为3 mm、输出光束发散角为0.2°、接收孔径180°、接收平面半径为0.25 m,接收机距离光源50 m,则光束投影在接收平面的半径为0.178 m。根据相关文献,GPS的定位误差大概在3 m[8],我们使用蒙特卡洛算法,在半径为3 m的圆内产生一万个均匀分布的点,然后采用不同的扫描方法,使发射机停留在按照某个步长间隔分布的点,采取不同的步长,计算出漏扫概率和扫描到接收板所需的平均时间。 假设矩形的扫描范围覆盖在GPS误差确定的圆的内接正方形内,示意图如图4所示。可计算出扫描覆盖范围为边长为4.243 m的方阵。显然,当扫描步长正好为接收板直径dv=0.5时,漏扫概率应该是很小的,因此我们将步长规定在dv±0.4 m的范围内,我们用扫描到接收板的需要停留的次数来作为衡量扫描时间的大小,数据如表1所示,然后将时间归一化,做出扫描时间和扫描成功的概率随步长的变化曲线如图5所示。 图4 规则内接矩形扫描方案 表1 概率和归一化时间随步长的变化数据 图5 规则扫描的时间和扫描概率 我们发现当矩形采用内接正方形时,漏扫概率最大也不到80%,说明这时另一部分随机点发射机永远也无法在此范围内扫描到。因此我们对扫描区域做了改进。 如图6所示,我们改变矩形扫描范围的边长,使GPS误差范围内边上的点可以被扫描,并且按照圆的轮廓限制扫描范围,此时扫描范围不再是矩形,但是路径依旧可以按照矩形路径扫描。同样按照上面的步长穷举法,仿真一万个点,我们求出了每种步长的平均扫描成功概率和平均花费时间得出的数据如表1所示,曲线如图7所示。 图6 不规则范围扫描方案 图7 方案二扫描的时间和扫描概率 我们根据数据样本对扫描花费的时间和漏扫概率两个指标进行归一化并线性加权,得到权重分别为0.8和0.2,按照II方案对步长进行穷举,得出不同步长的总得分。最后得到的最佳步长为0.367 m,这个点对应于图7中纵坐标-“扫描成功率”的转折点处。 我们设计的这种基于GPS的自主水下定位系统,结构简单,无需多加复杂设备,节省成本。且由仿真结果可见,它可以在比较短的时间内以较大的成功概率扫描到接收板的位置,而最佳扫描步长可以根据使用者权衡漏扫率和扫描时间的权重来决定,最终仿真并综合评价得到的一种最佳步长也与实际经验相符。在实际应用中,我们考虑将给出的两种扫描方案相结合,在保证一定低的漏扫率前提下,有望进一步减少扫描时间。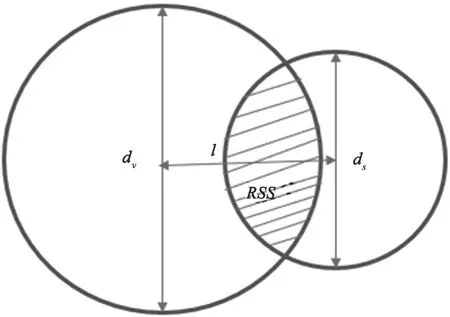
2.3 扫描轨迹
3 实验与仿真


4 结 语
