无线可充电传感网k-弱栅栏构建与移动充电调度*

李腾龙

（杭州电子科技大学 计算机学院，浙江 杭州 310018）

0 引 言

栅栏覆盖是无线传感器网络[1]的基本问题之一，根据入侵路线的不同，栅栏覆盖可以分为强栅栏和弱栅栏。栅栏覆盖广泛应用于环境监测、森林火灾检测等领域。由于传感器节点电池能量的限制，如何延长栅栏覆盖的网络寿命是[2]一个关键问题。现有的延长栅栏寿命的方法有两种：睡眠调度机制[2-7]和能量收集机制[8-9]。

Kumar[3]首先介绍了睡眠调度机制，通过控制无线传感器网络中传感器的工作睡眠状态，延长网络的生命周期。一般来说，基于睡眠调度策略延长网络生命周期的方法与网络中冗余传感器的数量有很强的相关性。

延长栅栏网络寿命的另一种方法是部署具有能量收集能力的传感器[8-9]。传感器节点可以将环境中的能量转换为电能[10-13]，因此，单个传感器可以工作更长时间，从而延长网络的使用寿命。具有能量收集能力的栅栏覆盖最初是在文献[2]中提出的，其目标是为栅栏应用提供最大的生命周期。

虽然睡眠调度机制和能量收集机制提供了可行的解决办法，但是仅仅维持栅栏的持续工作是不够的。一方面，通过控制构成栅栏的传感器激活状态可以延长网络的工作寿命，但是由于单个传感器电池容量的限制，其寿命也是有限的。另一方面，传感器节点在获取可再生能源的过程中往往受到环境的制约。例如，文献[14]中能量收集系统高度依赖于阳光直射的强度。

随着无线充电技术的发展，利用移动充电车[15-16]来延长网络寿命越来越受到关注。本文我们将采用移动充电车（Mobile Charger，MC）与可充电传感器构造可持续运行的k-弱栅栏。一个MC带着足够的电量从基站出发，分别访问栅栏中的每个传感器节点并对其进行充电，以保证k-弱栅栏持续运行，同时使MC在每个充电周期的平均能耗输出最小。

1 可持续工作k-弱栅栏与移动充电策略

本文的目标是构建k-弱栅栏监控区域内的入侵者，同时最小化MC的输出能耗，包括移动能耗以及充电能耗。在弱栅栏中，入侵者的穿越路径是垂直于监控区域的。

1.1 栅栏调度和移动充电策略

在一个长为L宽为H的矩形区域随机抛洒有n个静止可充电传感器，S={s1,s2,…,sn}。同时，区域中有一个MC为栅栏提供能量补充。

为了保证栅栏的可持续运行，我们在监控区域中构建k+1条弱栅栏以保证网络的k-弱栅栏覆盖，同时MC为另一条栅栏进行充电。

我们设置k-弱栅栏网络的运行时间片段为τ，在每个时间片段内，MC为一条栅栏充电，另外k条栅栏处于工作状态。网络的周期为T=(k+1)×τ，MC每个周期对每条栅栏充电服务一次，工作方式为一对一无线充电。

在每个周期T，每个传感器节点只有一次充电机会，传感器节点的初始电量均为E。传感器节点si单位时间能耗为ωi，当传感器节点的剩余电量小于Emin时，传感器节点将进入睡眠状态。因此，为了保证传感器在任意时刻的电量都不小于Emin，传感器节点si每次补充的电量必须不小于k×τ×ωi。

1.2 连续工作k-弱栅栏网络的分析

当无线传感器网络工作时，根据栅栏调度以及充电策略，我们可以得到网络的平均能耗，即MC的最小输出功率EAVE：

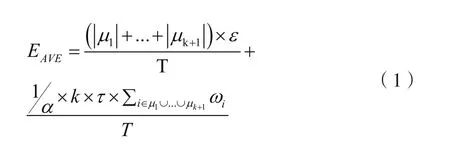
其中，μi是第i条栅栏的表示符号，|μi|是充电对第i条栅栏充电时的移动距离，ε是MC单位距离移动能耗，α是MC能量转化功率。在本文中，我们假定MC每次从左边界(lslot)或者右边界(rslot)的中心位置出发。如图1所示，MC需要对两条栅栏进行充电。

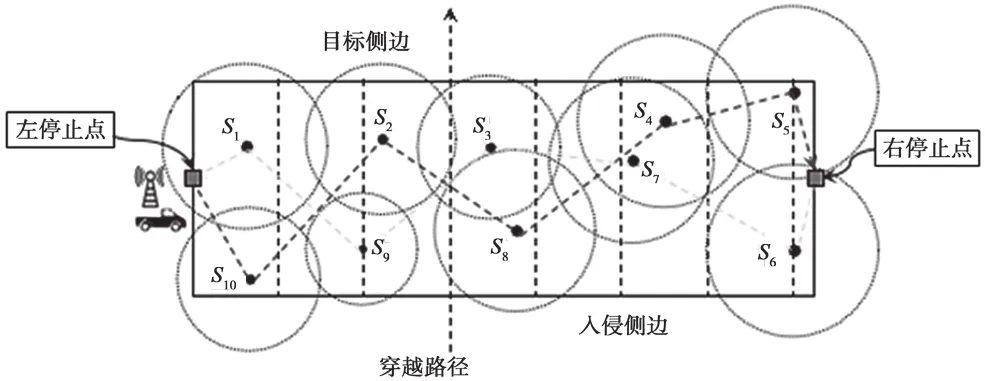
图1 充电车移动路径

为了保证节点在每个周期内不会能量耗尽而进入休眠状态，每个传感器节点的电池容量必须能够连续工作kτ的时间。因此：

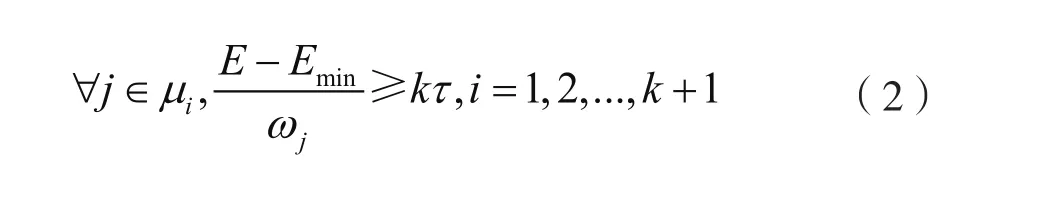
同时，MC必须能够在一个时间片段内完成充电任务，即MC在一条栅栏中的移动时间和充电时间必须小于等于τ：

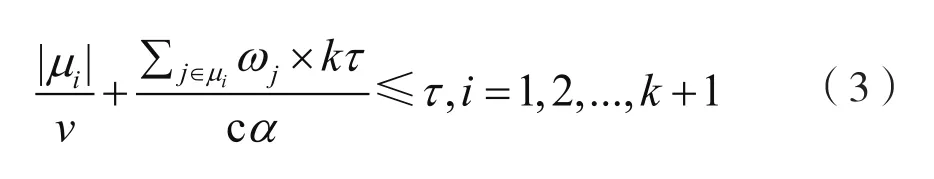
其中，v是MC移动速率，c为MC的输出功率。从式（2）和式（3）我们可以得到：

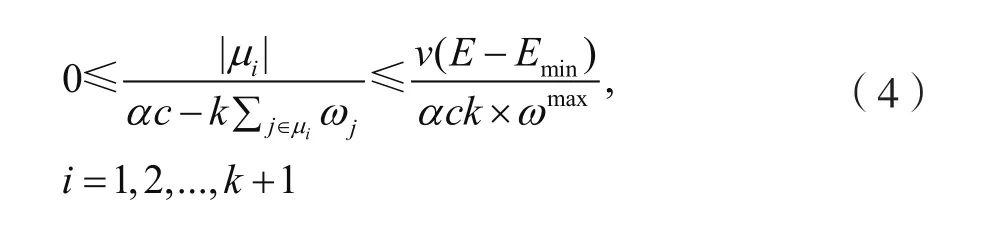
其中，ωmax是传感器节点的最大能耗速率。

MC每次从监控区域的一侧出发，沿着栅栏中传感器的位置依次进行充电。如图2所示，当监控区域的长度满足0<(L-rmin)mod(2rmin)≤rmin时，我们给出了一种长度最长的栅栏构造方法。传感器节点沿着监控区域的一侧依次排列，同时相邻两个传感器之间有一些空隙，另一侧的传感器节点对这些空隙进行填补。这种情况下构成弱栅栏的传感器节点最多有栅栏长度为：

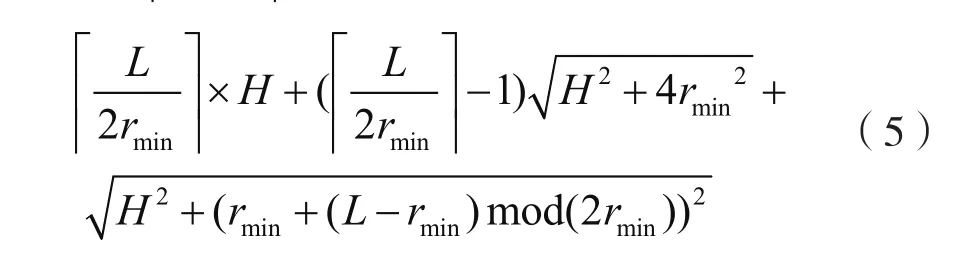
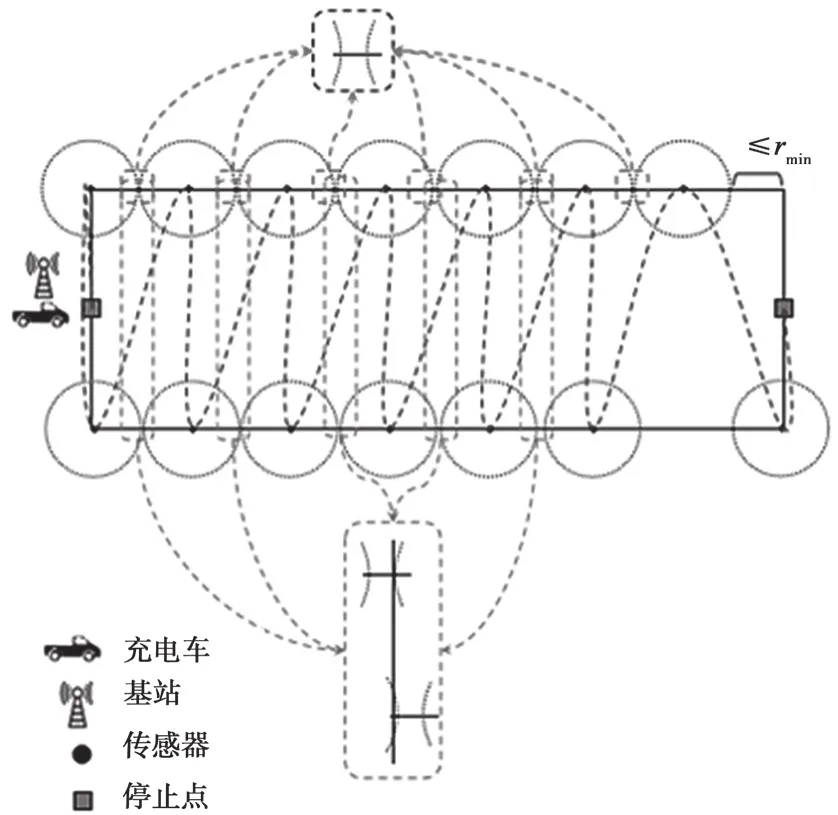
图2 当0<(L-rmin)mod(2rmin)≤rmin，充电车最长移动距离

如图3所示，当rmin<(L-rmin)mod(2rmin)或者(L-2rmin)mod(2rmin)=0，构成一条栅栏的传感器节点上界为于是，栅栏长度为：

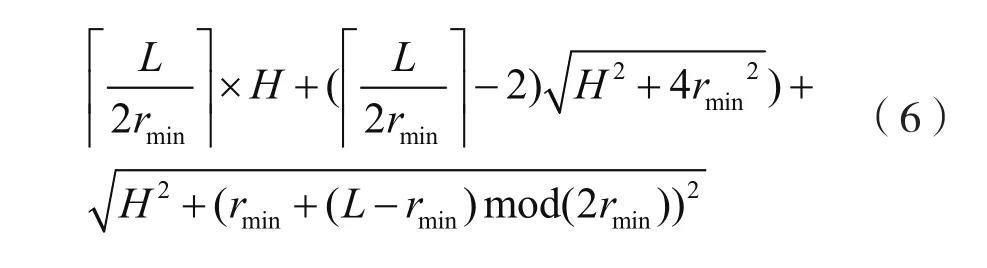
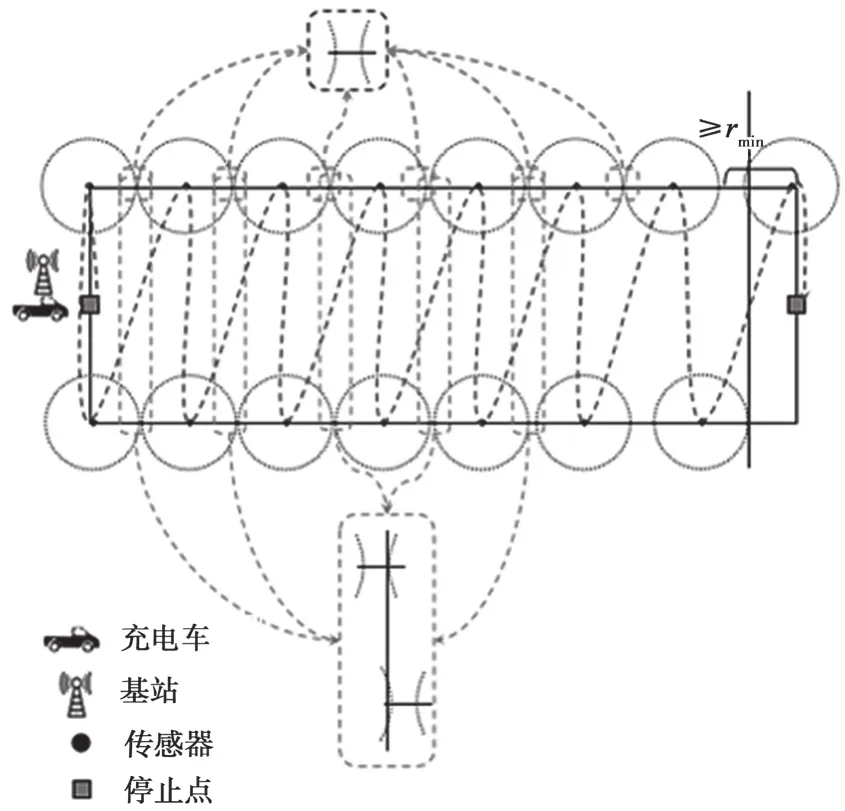
图3 当rmin＜(L-rmin)mod(2rmin)≤rmin或者(L-rmin)mod(2rmin)=0，充电车最长移动距离

如图4所示，我们在监测区域的左右两个停驻点连线位置从左到右布置传感器节点。除了最后两个传感器节点之外，相邻两个节点的感知范围恰好相互接触。这时构成弱栅栏的传感器节点的最小数目为同时，MC的最短移动距离为L。

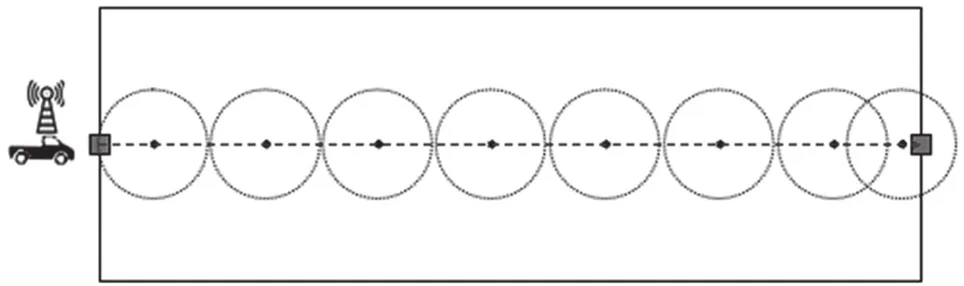
图4 充电车最短移动距离

于是，我们得到弱栅栏的长度范围：

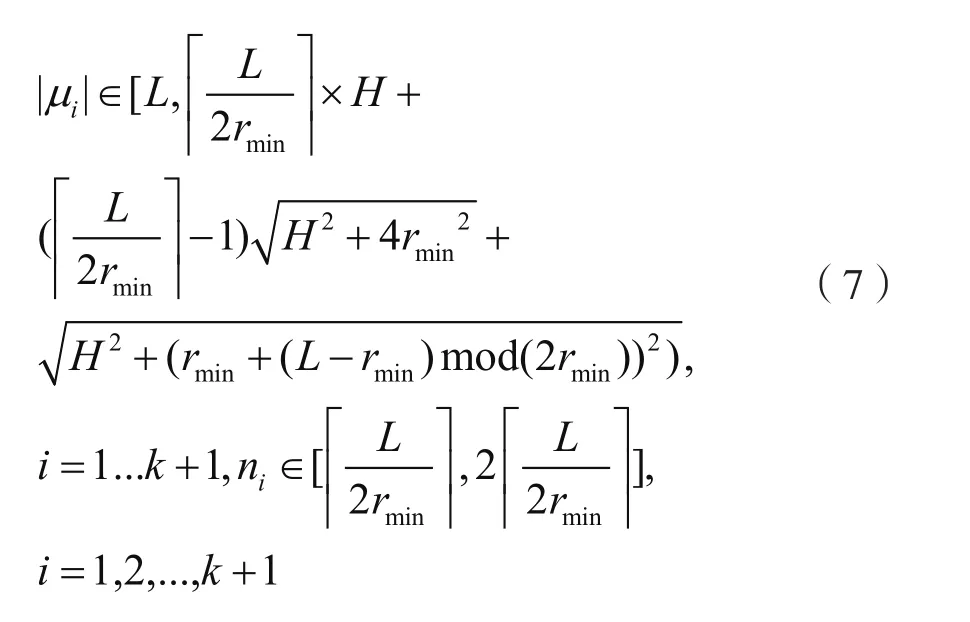
联立式（4）和式（7），可以得到：

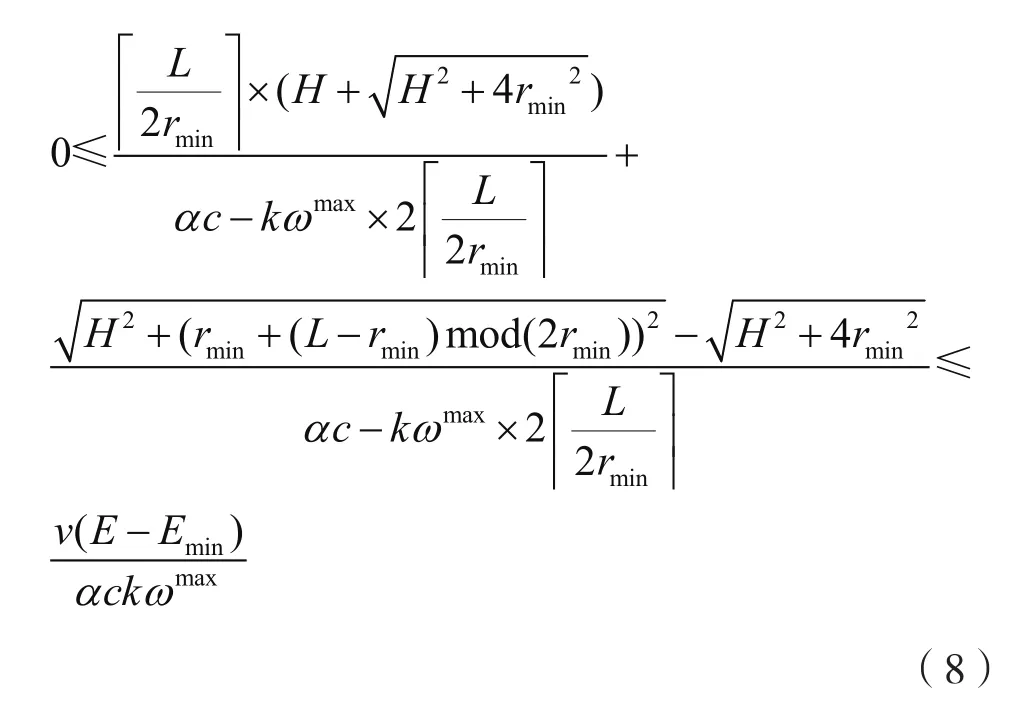
除了上面描述的限制条件，MC的能量必须要满足移动和充电的需求，即：接着，联立式（7）、式（9），可以得到：

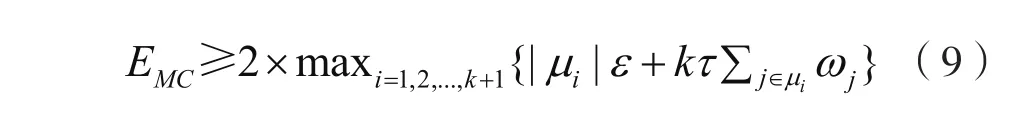
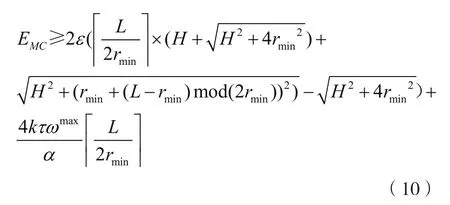
这样，我们得到了弱栅栏问题中，MC需要满足的能量条件，即式（8）和（10）。

我们的优化目标是最小化MC的输出能耗，即网络的平均能耗EAVE。从式（1）可知，网络周期T越长，网络的平均能耗EAVE越小。当无线传感器网络满足我们的约束条件时，可以得到一个可行的无线充电调度方案。同时，由式（2）可知，我们设置时间片段τ的大小为

2 最小能耗k-弱栅栏构造与移动充电调度算法

2.1 算法步骤

2.1.1 构建基础栅栏图

我们把lslot设置为左边界，把rslot设置为右边界。

（1）对于任意一个传感器节点s，如果它可以覆盖到左边界lslot，那么边〈lslot,s〉∈E，边对应的流量为1，即cap(lslot,s)=1。

（2）对于任意两个传感器节点si和sj，如果si和sj的感知区域在垂直方向上相互重叠，即|xixj|<(ri+rj)。那么，我们增加一条从si到sj的边，即(si,sj)∈E；相应的边流量为1，即cap(si,sj)=1。

（3）对于任意一个传感器节点s，如果它可以覆盖到右边界rslot，那么边〈s,rslot〉∈E，边对应的流量为1，即cap(s,rslot)=1。

如图5所示，在基本的栅栏构造图中，如果网络中存在k+1条不相交的路径，那么我们可以得到k+1条栅栏。同时，在一条栅栏中，除了左右两个停驻点之外，其它节点都有一个前驱节点和一个后继节。这保证了相邻两个节点之间的流量为1，但是这并不能保证每个传感器节点只属于一条栅栏。我们将在下一节中使用分割点为边的方法来保证每个传感器节点仅属于一条栅栏。

图5 基本栅栏构造图

2.1.2 分割点为边

在本章节中，我们使用分割节点为边的方法来限制节点的流量。如图6所示，对于每个传感器节点s，我们添加一个虚节点s´；接着，我们增加一条有向边〈s,s´〉从s指向s´，同时，我们设置边的容量为1。对于节点s与其它传感器节点之间边的关系，指向传感器节点的边都连向s，而从节点发出的边都从虚节点s´出发。而对于一条无向边来说，我们需要用两条有向边来表示，如图7所示。

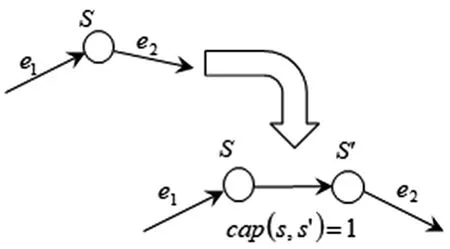
图6 分割点的方法

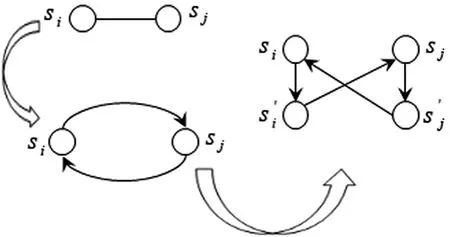
图7 无向图中分割点的方法

每一条经过节点s的流量必须通过边〈s,s´〉，因此，边的容量被限制为cap(s,s´)。分割节点为边是通过把一个传感器节点换成一条有容量限制的边的策略来保证节点不会被重复使用，即避免了栅栏相交的可能性，如图8所示。

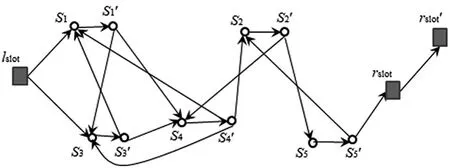
图8 栅栏覆盖图

为了保证栅栏数目为k+1，我们把节点rslot的容量限制为k+1。即增加rslot的虚节点r´slot以及有向 边〈rslot,r´slot〉。 边 的 容 量 为cap(rslot,r´slot)=k+1，费用为0。

2.1.3 权重分配

本章节的目标是找到最小的网络平均能耗EAVE，对于我们找到的k+1条栅栏，根据式可以计算出EAVE的值：

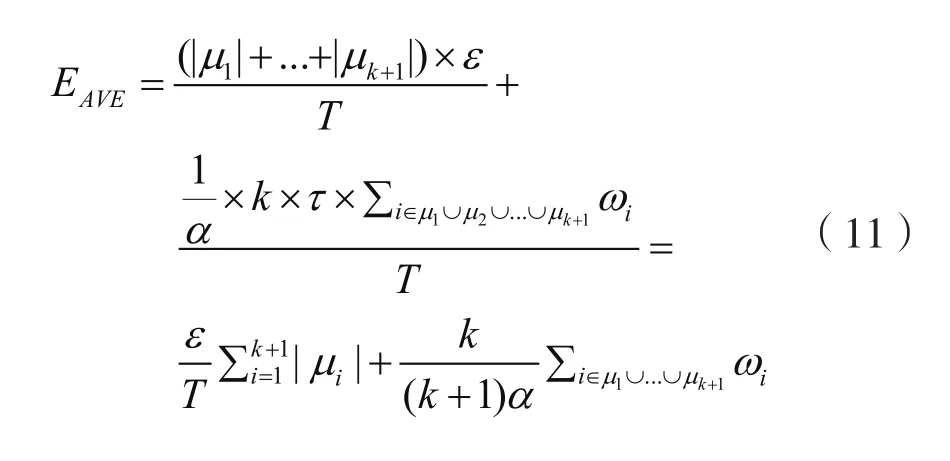
MC的输出能耗包括移动能耗以及对传感器节点充电需要的能耗。我们设置w1=ε/T，w2=k/(k+1)α。其中，w1为MC在每个周期T移动一个单位（米）距离的能耗，w2为一个比例系数，它表示当传感器节点的能耗速率为ωi时，MC每个周期T的能耗增量为w2×ωi。

我们为每条边设置相应的权重，可以得到一个完整的栅栏图。其中，顶点si与顶点s´i之间的有向边设置权重为w2×ωi。相邻两个传感器节点之间的有向边，即顶点si和顶点sj之间的权重为w1×dist(si,sj)，其中，dist(si,sj)为节点si与sj之间的距离。

2.1.4 最小费用最大流算法

引理1:栅栏图中最大流对应的传感器节点可以构造k+1栅栏。

证明：根据栅栏图构造的步骤1和步骤2，每个传感器节点si可以分割成两个节点si和s´i。同时，我们在节点si和s´i之间增加一条有向边，边的容量为1。这样，每个传感器节点的流量都被限制为1，传感器节点都具有一个前驱节点和一个后继节点。因此，从lslot到rslot的增广路径一定是相互排斥的。另外，我们把节点rslot的流量设置为k+1，因此，整个网络的最大流为k+1。在文献[3]中有k+1条不相交路径可以构建k+1条栅栏。

定理1：栅栏覆盖图的最小费用为EAVE。

证明：根据引理1，从lslot到rslot的增广路径一定是相互排斥的。我们假定一条增广路径为μi=〈lslot,sa,s´a,sb,s´b,…,sz,s´z,rslot,r´slot〉，相应的总费用增加的值为w1×dist(lslot,sa)+w2×ωa+w1×dist(s´z,sb)+w2×ωb+…+w2×ωz+w1×dist(s´z,rslot)+0=w1+|μ|+w2×(ωa+…+ωz)。我们记ψ=|μ1|+…+|μk+1|，那么，k+1 条增广路径增加的总费用为EAVE=w1×ψ+w2Σμ1∪…∪μk+1ωi。因此，栅栏覆盖图的最小费用为EAVE。

2.2 算法近似度分析

假定MC对单条栅栏进行充电时的最大移动路径长度为：

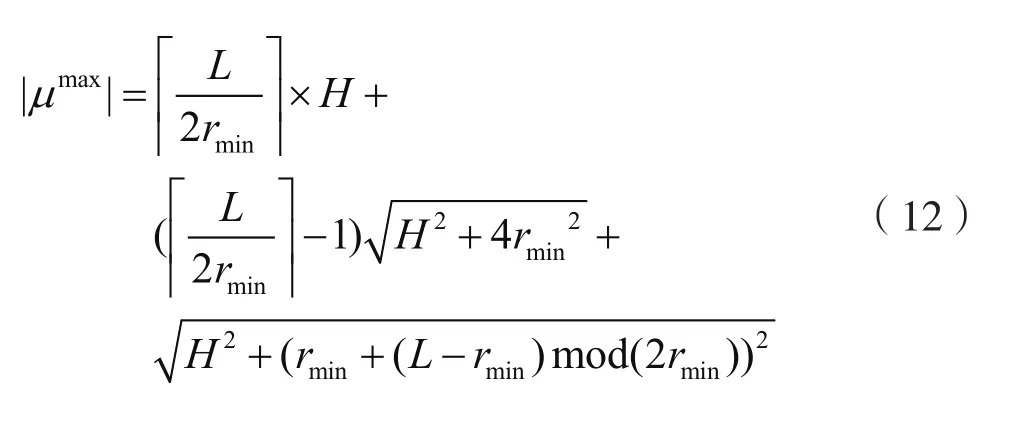
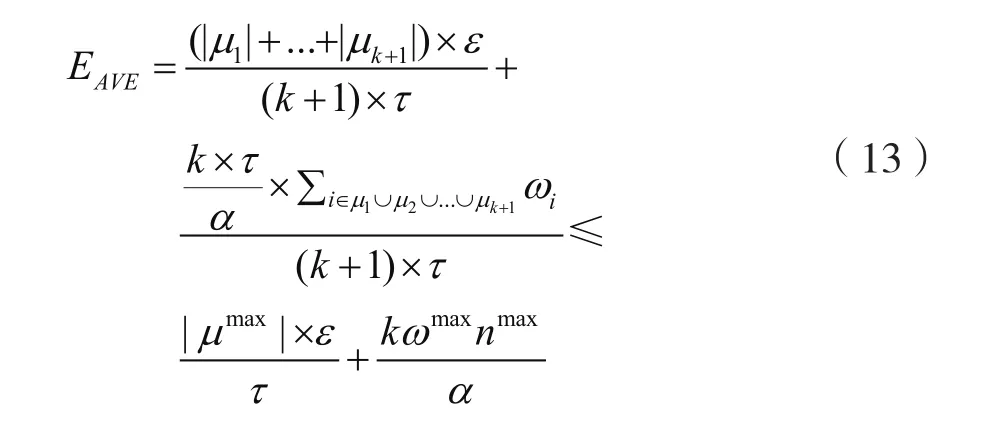
我们记问题的最优解为E*。当传感器沿着左右停驻点(lslot,rslot)位置的连线方向依次布置时，MC的移动距离以及充电能耗都可以得到最小值。同时，我们采用相同的周期计算网络的最优解E*：

根据式（13）以及式（14），可以计算出算法的近似度为O(k)：

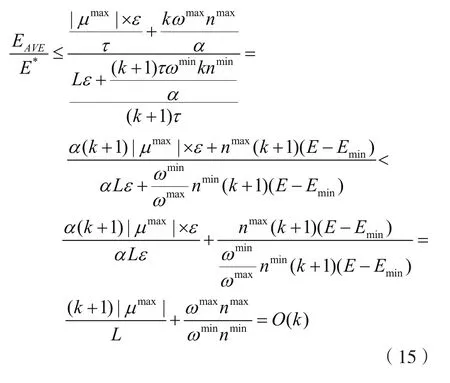
3 模拟实验

本章利用C++设计了模拟实验，并设计了一个贪心算法与我们的近似算法进行比较。贪心算法首先采用最小费用最大流求出k+1条栅栏，接着采用和近似算法相同的充电调度策略。

我们在一个矩形区域内随机抛洒了200个传感器节点，区域宽度为30 m，长度从100 m一直增加到300 m。同时设置传感器的初始电量为E=1 000 J，传感器si单位时间能耗为传感器节点的感知半径在19～23 m之间随机分布。MC电量满足一条栅栏的能耗需求，移动速率为5 m/s，移动能耗为100 J/m，充电输出功率为5 J/s，能量转化率为0.976 5。

如图9所示，在不同的区域长度下，我们提出的近似算法的平均能耗总是低于贪心算法的平均能耗。由于我们设置的传感器数目相同，当区域长度最小时，网络中传感器节点最稠密，近似算法相比贪心算法的能耗节约百分比越大。因此，面对密集型传感器网络时，近似算法的优化空间越大。

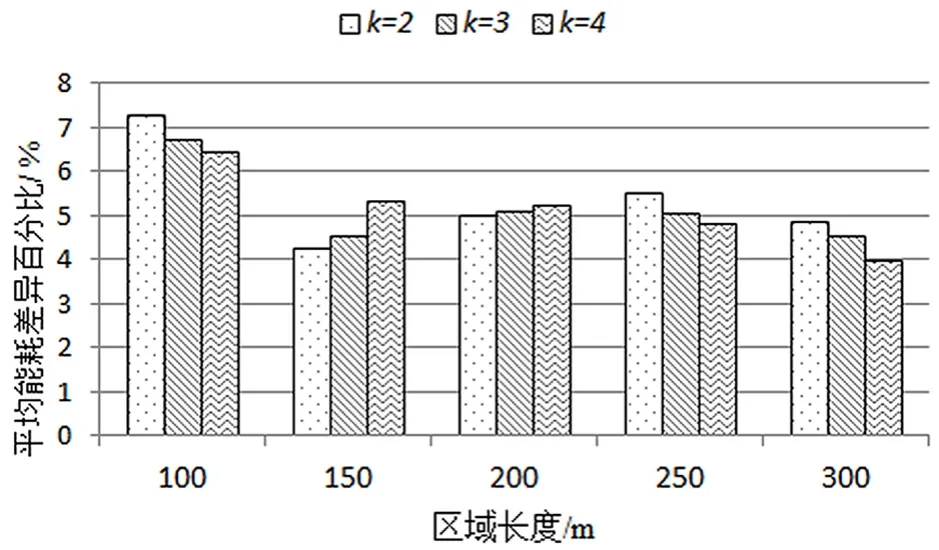
图9 不同监控区域长度时，近似算法网络平均能耗相比贪心算法每周期减少的百分比

如图10所示，我们在不同传感器感知半径下设置的节点数目是相同的，当半径较小时，构成相同长度的栅栏所需要的传感器数目越多，近似算法的能量节约百分比也越大。近似算法在构造栅栏时同时考虑了节点能耗和充电车移动能耗，所以当网络规模越大，传感器数目较多时，近似算法的优化空间越大，能耗节约率自然越高。

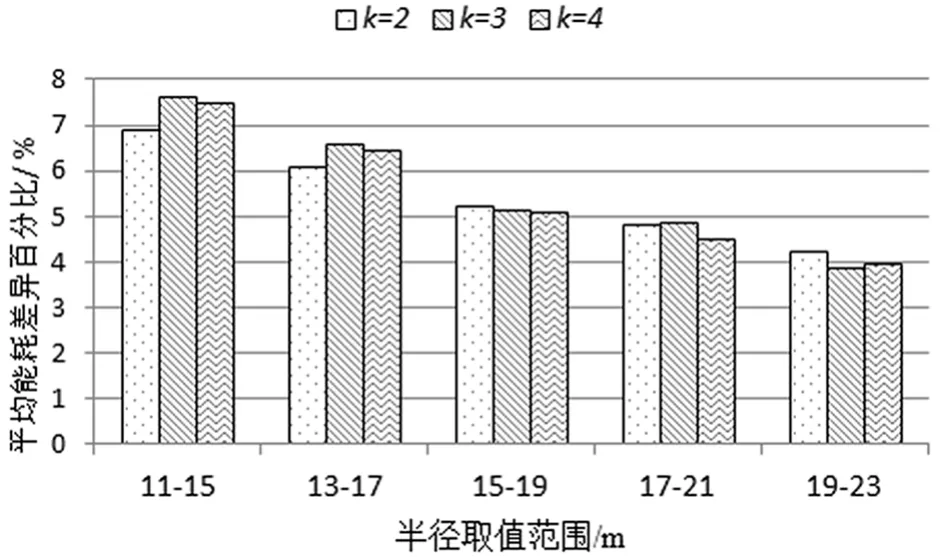
图10 近似算法网络平均能耗相比贪心算法每周期减少的百分比

4 结 语

本文提出了一种结合k-弱栅栏构造与移动充电调度的近似算法。我们以最小化网络平均能耗为目标，提出了最小能耗k-弱栅栏构造与移动充电调度问题。我们根据网络规模对问题进行了分析，设计了MC的循环调度策略与栅栏求解方法。最后通过模拟实验，证明了近似算法的有效性。