融合模拟退火和自适应的天牛须搜索算法*

周田江，钱 谦，伏云发

（昆明理工大学 信息工程与自动化学院 云南省计算机技术应用重点实验室，云南 昆明 650500）

0 引 言

在计算机研究领域，人们利用生物的自主行为或某些自然现象，模拟出一系列智能算法来解决最优化问题，如遗传算法[1]、模拟退火算法[2]等。遗传算法是一种模拟生物进化规律的算法，模拟退火算法是来源于对固体高温退火过程的模拟。这些算法一经提出就被应用于许多工程领域[3-4]。

天牛须搜索算法[5]（Beetle Antennae Search Algorithm，BAS）是于2017年由Jiang提出的一种新颖的生物启发智能优化算法，其思想源于对天牛觅食行为的模拟。BAS算法具有参数少、易于实现等优点，并且算法计算过程简单，通用且鲁棒性强，较少的受到初始条件约束，可用于求解复杂的非线性优化问题。该算法被提出后，就被应用于多个领域。文献[6]将BAS算法与反向传播（Back Propagation，BP）神经网络相结合应用于风暴潮灾害损失预测。陈婷婷等[7]提出基于天牛须搜索的粒子群优化算法，并将其应用于投资组合模型中。邹东尧等[8]在基于接收信号的强度（Received Signal Strength Indicator，RSSI）测距的基础上，将BAS算法应用到室内定位中，有效的提高了定位的精度。Wang J等[9]对BAS算法进行了深入研究，提出了天牛群搜索算法（Beetle Swarm Antennae Search Algorithm，BSAS）。文献[10]将混沌序列引入天牛群算法，提出了一种带有群体学习与竞技的群智能优化算法。

本文作者在大量实验研究中，发现在多维函数优化问题中（例如维度大于4），BAS算法收敛速度慢、寻优精度低，单独利用单个天牛的搜索方法大大增加了算法陷入局部极值的可能。针对这一问题，本文提出了融合模拟退火和自适应的天牛须搜索算法（Simulated Annealing and Adaptive Beetle Antennae Search Algorithm，SABAS）。该算法将天牛须的感知与固体退火过程相结合，有效的避免了基本BAS易陷入局部最优的问题。同时，引入自适应因子，加快了算法的收敛速度。多维函数优化仿真结果表明，改进的天牛须搜索算法具有更好的寻优能力。

1 BAS算法基本原理

天牛须搜索[11]（BAS）算法是模拟天牛觅食行为的智能优化算法。当天牛觅食时会利用左右触须来感知食物的气味强度，如果左边触须收到的气味强度大，它下一步就往气味强度大的左边飞，否则往右边飞。BAS算法中天牛的当前位置即为所求解问题的一个可行解，食物的气味强度即为适应度函数。本文以多维函数优化为例求解最优值（最小值），建模步骤如下：

（1）假设天牛个体在k维解空间中的位置为X0=(x1,x2,…,xk)；

（2）创建天牛左右须空间坐标：

式中，t是算法循环次数；d是天牛质心与触须间的距离；b是随机单位向量，表示天牛在空间中的朝向，取右须指向左须的方向为天牛的朝向。

（3）更新天牛的下一步位置：

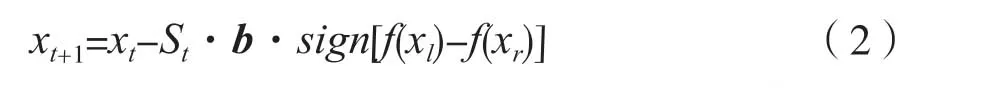
式中，f(x)是x的适应度值；St表示在第t次迭代时的步长；sign()是符号函数。在实际研究中，Jiang[5]提出St=α·St-1，α为步长因子，一般设为0.95，该步长因子按比例减小搜索步长，可以有效提高算法的寻优性能和收敛速度。

2 SABAS算法

2.1 基于模拟退火的寻优

模拟退火[12]（Simulated Annealing Algorithm，SA）算法是一种模拟物理中固体物质的退火过程的智能算法，该算法具有能找到全局最优解且收敛速度快的优点，其在搜索过程中具有概率突跳的特征，这使得该算法可以有效地避免陷入局部极值。具体来说，SA算法在搜索过程中除了接受好的解，同时还可以以一定的概率接受差的解，而此概率受到温度参数的影响，其值的大小随温度的下降而逐渐减小，这就使得算法在前期有较大概率跳出局部极值，而在后期又能具有较高的收敛速度。SA算法通常以Metropolis准则[13]作为是否接受新解的依据，准则如下：

计算增量ΔT=f(xt+1)-f(xt)；

若ΔT<0，则接受xt+1为新解；

否则计算p=exp[-ΔT/T]，以概率p接受xt+1为新解。式中，exp()是以自然常数e为底的指数函数；T为当前温度。由于T随迭代次数递增而减小，故p值也随之减小。

在多维空间里，BAS算法中的天牛个体只在当前位置感知下一步位置的方向，则很大程度会陷入局部极值[10]。针对BAS算法的这一缺点，本文把模拟退火算法的退火过程融入到BAS算法中，使得BAS算法有一定概率接受较差解，有效地避免了BAS在多维度情况下易陷入局部最优的问题。

在改进的算法中，存在两层循环。外循环中利用当前温度T控制基本BAS中的天牛初始步长S，在内循环中使用Metropolis准则更新天牛下一步位置，温度T随迭代次数递增而减小，故天牛的步长也随之减小以达到收敛。

通过对改进后的算法进行实验研究，发现在天牛搜索过程中，当天牛的下一步位置比当前位置好时，天牛移动到下一步位置；否则，如果下一步位置比当前位置差，天牛会以概率判断是否进行移动，且通过温度T来控制此概率。这样天牛不会进行盲目的移动，而是通过判断后再移动，使得天牛有概率跳出局部极值。并且天牛的步长S同样被温度T控制，在外循环过程中，天牛的步长随退温操作而逐渐减小，从而更快的搜索到最优位置。

2.2 自适应因子

在BAS算法[9]中，参数步长因子α是控制算法收敛快慢的关键，步长大小与因子α息息相关。具体原因如下：

（1）如果步长衰减得足够缓慢，全局搜索能力越强，但与此相对的是收敛速度太慢；

（2）如果步长衰减得过快，很可能得不到全局最优解。

步长因子实现对算法收敛速度的控制，步长因子越大（趋于1），收敛速度越慢，但全局搜索能力强；反之因子越小（趋于0）收敛速度越快，但容易陷入局部极值。然而，基本BAS中的步长因子在寻优过程中是固定不变的，为了让算法获得更好的寻优能力，本文提出动态改变步长因子的改进方法。具体来说，在寻优前期，为了扩大在解空间整体的搜索范围，加快寻优速度，应该采用较大的步长因子；在寻优后期，搜索解趋于稳定，为了使解的精度更高，应该减小步长因子。另外，初始步长因子越小，越容易陷入局部极值，所以应给与较高的初始值，如0.95。

基于上述考虑，设置如下调节机制：

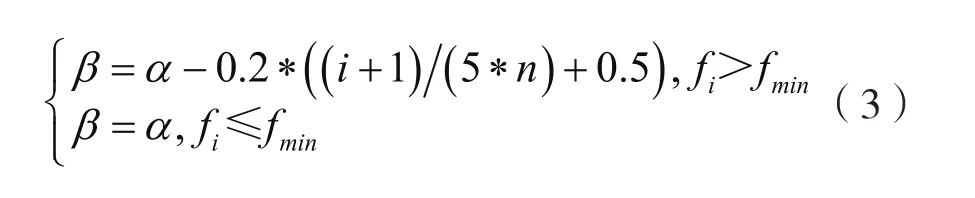
式中，fi是当前适应度值，fmin是历史最优适应度值，i是当前迭代次数，n是迭代总次数，α是默认步长因子（一般为0.95），β是当前步长因子。式中表明，当当前适应度值小于历史最优适应度值时，表明目前寻优性能良好，此时保持步长因子默认值，用以保证做到全局搜索；反之，则认为寻优性能不佳，减小步长因子以加快收敛速度，与此同时随着迭代次数的递增，最小适应度值趋于稳定，应使步长因子的减幅扩大。

2.3 SABAS算法步骤

步骤1：初始化天牛的位置X，温度T，步长因子α，迭代次数N，退火循环次数L；

步骤2：设置天牛的步长S=T；

步骤3：根据式（1）和式（2）得到天牛下一步位置X´；

步骤4：根据Metropolis准则更新下一步位置X；

步骤5：更新步长S=α*S；

步骤6：判断是否达到退火循环次数L，如果满足执行步骤7，否则返回步骤3；

步骤7：按式（3）更新自适应因子β；

步骤8：退温操作T=β*T；

步骤9：判断是否达到迭代次数N，如果满足输出当前天牛的位置作为最优解，否则返回步骤2。

3 仿真实验及结果分析

3.1 测试函数

为了验证 SABAS 算法的性能，对6个具有代表性的基准测试函数[14-16]进行仿真实验，并将测试结果与BAS、BSAS和SA算法进行比较，BSAS算法的具体实现详见文献[9]。表1给出了6个基准测试函数的名称、函数表达式、解搜索空间范围和最小值。其中，D是变量的维数，F1和F2是单峰值函数，F3-F6为多峰函数。

表1 测试函数

3.2 测试方案

实验采用Python 3.6.5进行仿真实验。四种算法的实验参数为：设置每个算法的最大迭代次数N=200，在SABAS中，退火循环次数L=100，初始温度T=200，自适应因子α=0.95，算法中计算适应度函数的次数（即寻优次数）为200*100次；在BAS中，初始步长S=200，步长因子α=0.95，由于BAS中只有单个个体且无退火循环过程，为了客观地与其它算法进行对比，测试中BAS并行运行100次然后取最佳结果，因此整个算法过程寻优的总次数也为200*100次；在BSAS中，种群数P=100，初始步长S=200，步长因子α=0.95，由于包含了复数个天牛个体，算法的寻优总次数同样为200*100次；在SA中，退火循环次数L=100，初始温度T=200，退火因子α=0.95，算法的寻优总次数为200*100次。为了确保评价的公平性及客观性，在测试中，四种算法独立运行50次，取实验结果的平均值进行比较。此外，本文采用平均最优解（Average Optimal Solution，AOS）和平均收敛到最优解代数（Average Optimal Iteration，AOI）这两个指标来反应算法的性能。

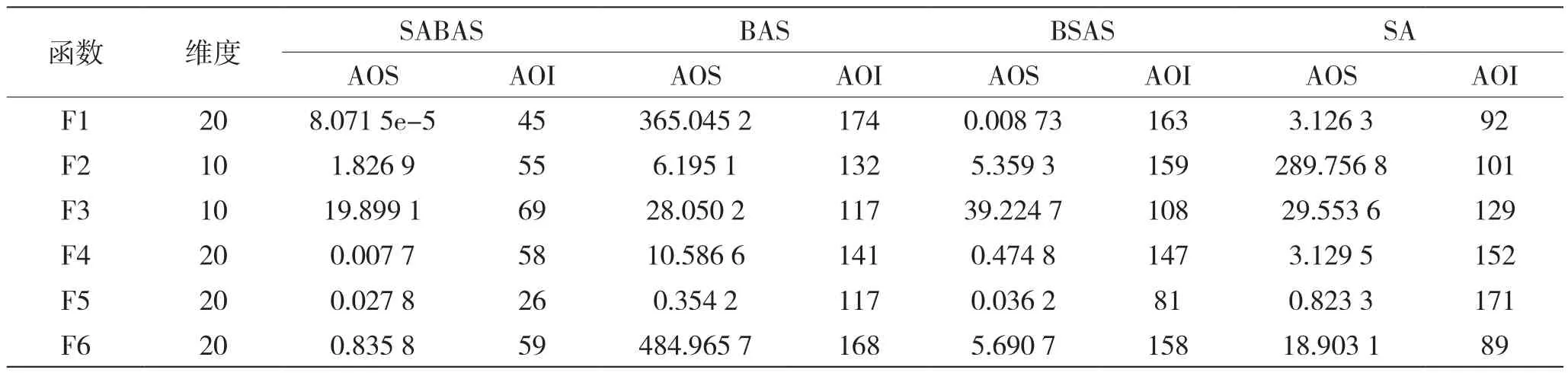
表2 性能参数对比

从表2中的数据对比可以看出，SABAS算法相较于基本BAS和BSAS算法在寻优结果上有显著优势，在收敛速度上也有明显提升，特别是对F4函数的优化，其它三种算法都陷入了局部极值，只有SABAS算法跳出了局部极值。实验结果表明，BAS算法虽然具有一定的全局寻优能力，但该算法不容易跳出局部极值，而SABAS算法的模拟退火过程使算法可以以一定概率跳出局部极值，并且SABAS算法的自适应因子机制使算法具有更高的收敛性能。

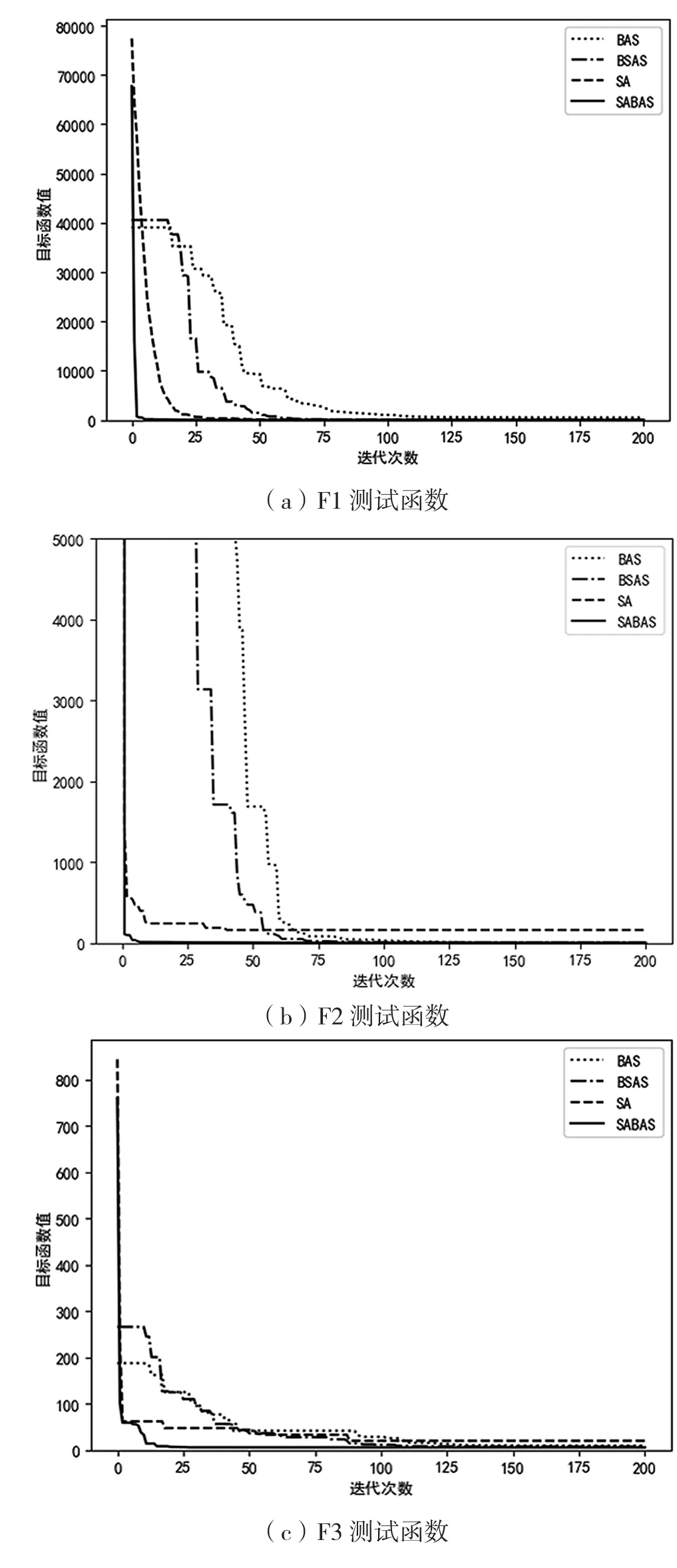
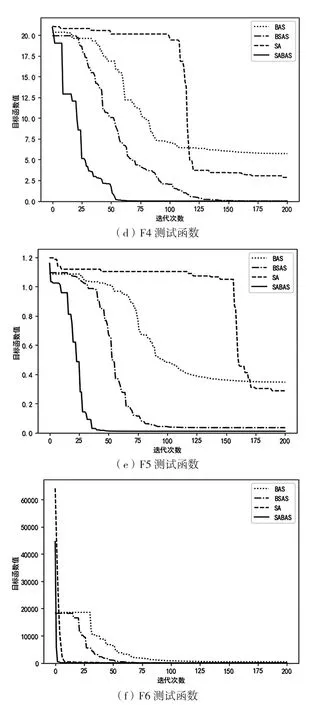
为了更直观地反应算法的性能，各函数4种算法收敛曲线如图1所示。横轴表示算法的迭代次数，纵轴表示寻优的目标函数值。其中BAS算法的目标函数值是100次并行运行中每次迭代的最优值。由于测试函数F2初始值较大，不利于直观反应算法的性能，因此设置了目标值的上限。SABAS算法在6种测试函数中都呈现平稳快速下降的趋势，体现了该算法的稳定性，同时也表明了自适应因子在一定程度上加快了该算法的收敛速度。而BAS、BSAS和SA算法在函数F4、F6的优化中很难达到SABAS在相同条件下所能达到的最优解。在对F2、F3函数的优化中4种算法都没有寻找到最优解，但SABAS相较于其它3个算法还是有着明显的优势。因此，SABAS算法的收敛性能以及寻优能力都优于其它3个算法。

4 结 语

天牛须搜索算法是一种新型的生物启发式智能算法，基本BAS算法在多维度条件下存在收敛速度慢、精度低和容易陷入局部最优等缺陷。针对BAS的不足，本文提出了把模拟退火算法的退火过程和自适应因子融入到天牛须搜索算法中的混合算法（SABAS）。该算法利用天牛须的感知与固体退火过程相结合，有效的避免了基本BAS易陷入局部最优的问题。同时，引入自适应因子，加快了算法的收敛速度。最后，通过仿真实验表明，SABAS算法在多维度函数寻优中有较好的寻优能力。