烟叶真空回潮的建模与控制
2019-09-04郝玉山李新叶杨海涛潘占良
郝玉山,李新叶,杨海涛,潘占良
1 华北电力大学 电气与电子工程学院,河北保定 071003;
2 保定市三川电气有限责任公司 研究所,河北保定竞秀街295号 071051
作为卷烟的第一道工序,真空回潮工艺过程[1]为抽真空后同时喷水喷汽,水在高速蒸汽带动下雾化进入烟包,使得烟包回潮而松散,同时灭菌、减少青杂气。然而,真空回潮还存在回潮能力不足、出口水分不一致和回透率偏低等问题,尤其是水分不一致将影响卷烟质量的稳定性。
长期以来,回潮箱内量如烟包温度和水分不可测,称为“黑箱”,只能测得压力作为阀门的开关条件而非闭环反馈量,即使采用了PLC智能化设备[2]的真空回潮控制也只能是开环控制[4]。由于时间常数大、延迟大,真空回潮的反馈控制难于实现[3]。不仅质量指标在线难落实,而且开环控制不能减小蒸汽、来料和环境等波动对回潮水分的影响。
可观测是自动控制的基础[4]。对于线性系统,能够通过观测方程由输入量U和输出量Y求得状态量X,条件是矩阵C可逆。但是,观测方程如何获得却研究不多,尤其是非线性系统的观测方程,文献更少。
在河北中烟建议的启发下,我们将电力验证成功的大数据建模技术[11]用于真空回潮控制,研制了真空回潮实验机,获得输入输出数据,试验表明真空回潮机可观测,能够算得真空回潮非线性的4个状态量,且误差可接受,还可获得回潮机的特性参数,按参考模型的积分控制,能够大幅度地提高真空回潮机的回潮能力、稳定出口水分和温度,还能够提前设定出口水分,改善回透率,降低回潮过程中的烟包温度,充分体现出建模控制后的精准、智能特性。现场应用后可望节省蒸汽热能、减少造碎、提高出丝率。
1 由大数据构建数学模型
真空回潮箱内压力P、温度T、烟包温度Ty和水分sy是真空回潮的状态量上标T为转置。
1.1 理论的解析模型
机内温度在喷嘴周围最高,烟包内部最低,机内各处温度不同、分布不均匀,是温度场:热源为喷嘴,机箱为边界条件,计算机能够求解偏微分方程的数值解[5],然而,不能解析,得不到解析模型。
机内压力P包括湿汽分量Pw,因重力影响,Pw会随着机内高度的降低而升高,所以,P是高度和时间的函数,是偏微分方程,也得不到解析模型。
烟包放在烟筐内,烟筐放在回潮箱下部,并且,上下、左右、前后都与机箱隔开,烟筐还要移动、回潮箱又密封,所以,烟包温度和水份都不可测,更不可能通过温度场、水份场推导出它们的解析模型。
1.2 大数据建模原理
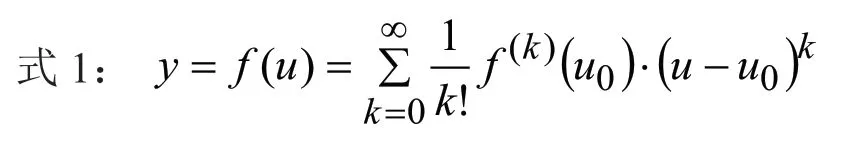
阶数衰减很快,取前k项忽略后续项,当k=6时,式1改写为,
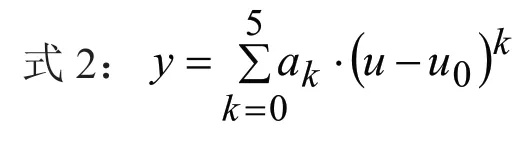
u0一般取为额定工作点;由N组输入输出数据{uj,yj,j=1,2,…,N},求得系数{ak,k=0,1,…,5},获得式2。
式2与式1的误差在10-6之内[11]。工程上1%即10-2精度足够,于是,问题得解。
对于多个自变量,结论同样成立。
1.3 获得数据
1.3.1 测点
为了获得输入输出数据,我们研制的真空回潮实验机外形见图1,增加测点,如蒸汽流量Dz、温度Tz和压力Pz,喷水流量Ds和温度Ts,烟包质量Myo、入口水分syo和入口温度Tyo,室温To和机箱温度Tx,机内上下压力P1和P2、机内上下左右的温度T1~T4等。

图1 真空回潮实验机的照片(回潮箱500×700×1200)Fig.1 Photos of the prototype of vacuum pre-conditioner
1.3.2 采样数据处理和稳态数据处理
利用输入输出数据辨识动态模型的参数,国内外有很多成功案例,如轮船和飞机的自动驾驶等[9、10],但是,鲜有2阶以上的成功案例,也就是说辨识参数的国际最高水平为2阶动态模型的参数[11],而真空回潮的动态模型为4阶,要辨识其参数必须有所突破。为此,对采样数据进行数据处理[13、11],滤除高频干扰、降低采样频率,让采样频率既满足下限[6]要求,又满足上限[12]要求,再辨识模型的参数[13]。
除了动态模型外,要获得状态量的观测方程,还需要稳态模型;要构建稳态模型就需要稳态数据。由于输入和输出的采样数据中不仅含有稳态数据,还含有动态数据,在电力自动化中,称为坏数据,自1970年国际上发现坏数据以来一直存在了40多年[11];如果直接将采样数据用于构建稳态模型势必导致模型有偏,为此,数据还需要稳态处理[14、11],以剔除坏数据、提高采样数据的同步性[15]。
1.4 建模方法
由输入输出数据求得式2系数的方法很多,如人工智能的神经元方法[7],将系数看成神经元之间联络的权重;再如优化数学[8]也能估计出系数;参数辨识不仅能够获得稳态模型的系数,还能够辨识出动态模型的系数[9]。
由蒸汽特性能够构建蒸汽的稳态模型,由温度、压力和流量,修正蒸汽流量和蒸汽量、算出蒸汽的热流量qz和热量Qz;由温度和流量,算出喷水的热流量qs和热量Qs。
由大量的输入输出数据构建出数学模型,记,

机内温度模型T(U)说明机内温度T是蒸汽量Sz、蒸汽热量Qz、喷水量Ss、喷水热量Qs、室温To、烟包质量Myo、入口水分syo、入口温度Tyo的函数。
同理机内压力模型P(U)、烟包温度模型Ty(U)和烟包水份模型sy(U)。
1.5 模型检验
用其它时段的数据来检验模型。
1.5.1 机内压力模型的检验
机内压力会随着高度而变化,机内上下压力P1和P2的均值能够代替机内压力。
由图2可见,模型算得的机内压力,与之间的误差在1%之内。
1.5.2 机内温度模型的检验
机内上下左右的温度T1~T4的均值 代表机内温度。
图3(a)示出由模型T(U)求得的机内温度和,图3(b)为它们之间的误差。
由图可见,温度模型误差在1%之内。
1.5.3 烟包温度和水份模型的检验
观测到的烟包温度和水份如图4和图5所示。

图2 机内压力模型输出及其误差Fig.2 Outputs and errors of the pressure model
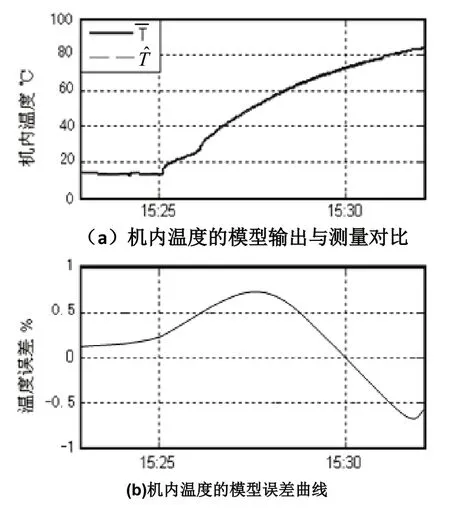
图3 机内温度模型输出及其误差Fig.3 Outputs and errors of the temperature model
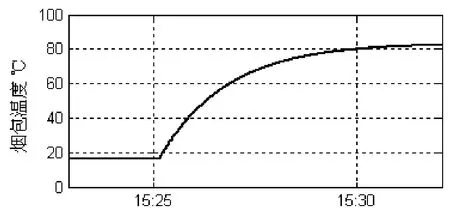
图4 烟包温度的模型输出Fig.4 Outputs of temperature Model of cigarette packed

图5 烟包水分的模型输出Fig.5 Outputs of moisture model of cigarette packed
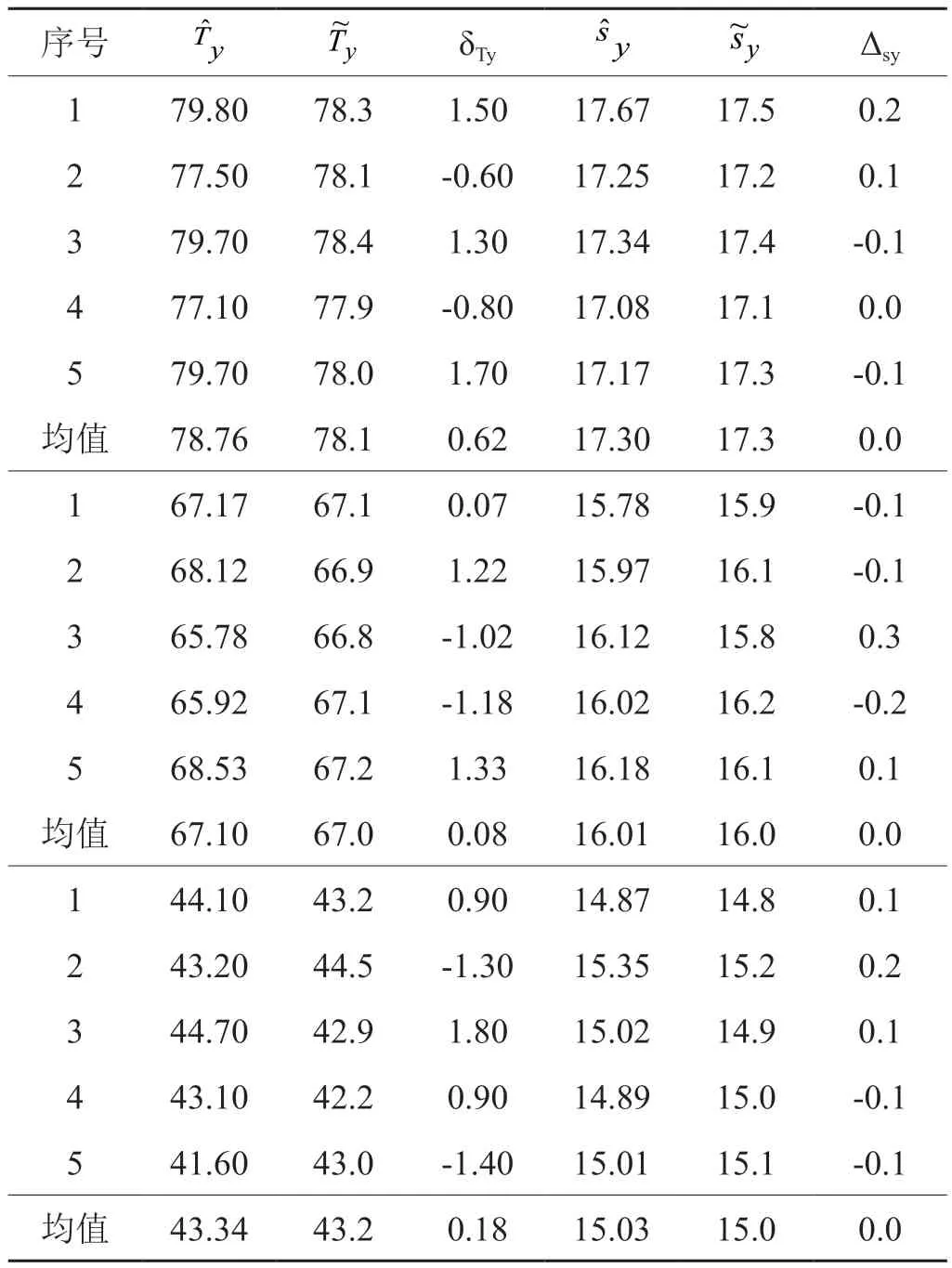
表1 烟包温度和水分的模型误差Tab.1 Model errors of the temperature and moisture of Cigarette Package
1.5.3 烟包温度和水份模型的检验
观测到的烟包温度和水份如图4和图5所示。
由于烟包在机箱内部,不便安装测点,所以,只能去掉二次抽空过程、开门后立即将温度探头插入烟包内部测量温度。
烟包高度上分三层、每层九点分别取样20g,按烘箱法测量水分后平均作为烟包水分。
和作参考标准,表1示出模型输出的烟包温度 和水分 及它们的误差。
由表1可见,烟包温度模型的误差在2%之内、水分模型的误差在0.5%之内。
1.5.4 小结
由输入输出数据,能够构建真空回潮机的稳态模型,给出回潮开始时状态量的初始值X(0);还能构建动态模型,状态量对时间的微分方程,从而,得知状态量每时每刻的值X(t)。
控制需要观测方程,以求得状态量X(t)。
所以,由数据构建的稳态模型、动态模型恰好形成自动控制的观测方程,并且,适用于多入多出的非线性系统。
模型检验表明,观测到的状态量误差在可接受的范围内。
2 控制器的设计
2.1 对象特征
2.1.1 非线性、多入多出
由图2(a)、图3(a)、图4和图5的曲线表明,机内压力、温度、烟包水分和温度对时间的函数关系各异,压力呈近似的指数关系,而温度近似线性关系,水分成对数关系,所以,机内模型属于非线性、多入多出MIMO系统[4]。
非线性系统与线性系统不同,线性空间的最优控制理论不可用,更不能用经典反馈控制的设计方法[4]。
2.1.2 时变、大时延
由输入输出数据辨识到的真空回潮机动态模型是变时间常数的大时延系统。
以烟包温度为例,来说明时间常数是变化的。
进入烟包的热量dq一方面通过湿汽的热流量qq获得,它是机内压力P、温度T和湿度d的函数 ,另一方面用于烟包温升dT,烟包包括干烟和水份,有微分方程:
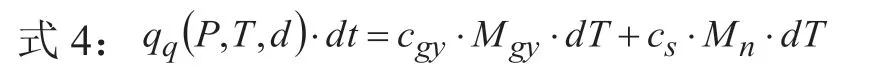
所以,

其中,cgy干烟比热系数、Mgy干烟质量、cs水比热系数、Mn回潮水份所对应的质量。
由于回潮水份是湿汽不断累积的过程,所以,Mn逐渐变大;作为一阶微分前的系数,相当于时间常数,也会逐渐变大。故,机内温度的时间常数是时变的。
同理,机内压力、温度和烟包水分的时间常数也是时变的。
2.1.3 蒸汽同时含有热和水
蒸汽是一种复合物,既包括水,蒸汽量即为水量;也包括热量,用热流量来计算。
如果需要增加热量,调节阀门开度,加大蒸汽流量同时,既增加了热量,又增加了水量。由于真空回潮机内压力低、汽化温度低,所以,喷水被汽化为气态,势必导致机内压力上升。所以,蒸汽作为输入量不解耦,会同时增加(或减少)热量与水量,导致状态量机内压力和温度的不解耦,必须按MIMO系统,而不能作为多个SISO系统进行设计[4]。
2.1.4 烟包内的液化速度不可控
机内顶部喷入蒸汽和水后,由于机内上部温度高于汽化温度,喷水汽化为汽,与机内剩余的空气、喷入的蒸汽混合后成为湿汽。湿汽在重力作用下自上而下运动,包围了放在机箱下部的烟包;在内外压差的作用下,湿汽自外而内运动;遇到烟片,由于烟片的温度低,导致湿汽温度低于汽化温度而液化成水、渗透到烟片内,从而完成回潮[16]。
顶部的汽化速度可控,通过调节喷水流量或喷入的蒸汽流量来控制汽化的进程。然而,回潮机本体不作改动的情况下,烟包内的液化速度不可控,需要设计控制器时予以考虑。
2.2 回潮控制器
对于非线性、时变、多入多出系统,没有解析的设计方法,只能另辟蹊径。
2.2.1 仿真训练参考模型
利用已建数学模型,采用数字仿真,在计算机上进行仿真训练,在回潮时间不超过15min约束条件下,按人工智能AI算法获得增加水分最大化的模型R(t),其4个分量分别是机内压力、温度、烟包温度和水分,其中的机内压力模型曲线如图6所示。
烟包内部的液化速度不能干预而是自然过程,控制使得上部的汽化速度与液化速度匹配,才能够达到多回潮的目的。蒸汽热量不能太少,太少将导致喷水不能充分汽化、顺壁而下直接成凝结水;热量太多也会导致烟包的温度上升而影响液化能力。
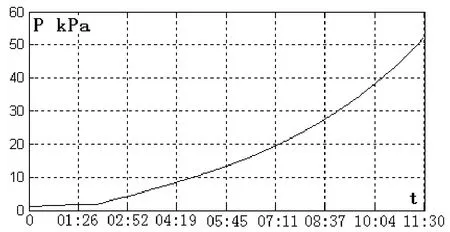
图6 机内压力模型曲线Fig.6 Outputs of pressure models trained
参考模型是仿真训练的结果,众多情况下找出的回潮水分最多;由模型仿真获得数据,比实验数据快很多,仿真两周数据足够,试验两月数据也不足。
2.2.2 跟踪参考模型
要状态量与参考模型的误差积分为零,原理框图如图7(a)所示[10],其中u为输入,r为参考模型输出,y为被控 对象输出,ζ为干扰。尽管被控对象的输出受到干扰的影响,然而,由于积分反馈的作用,被控对象必须与参考模型一样,其输出与参考模型的输出一样,而参考模型不受干扰的影响,所以,被控对象的输出也不受干扰的影响。
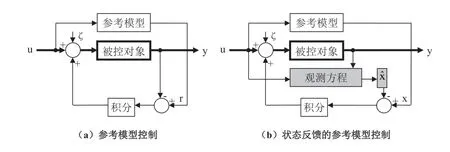
图7 参考模型控制原理图Fig.7 Schematic of reference model control
由于图7(a)的参考模型和被控对象中都有惯性环节,导致这种积分控制难于稳定。
于是,烟包水分和温度等将不再受来料、蒸汽、喷水和环境温度的影响。
3 控制效果与分析
3.1 水分一致性试验
3.1.1 蒸汽变化的影响
实验室的蒸汽压力和温度变化剧烈,有必要试验蒸汽变化对回潮水分的影响。
表2为蒸汽压力和温度变化后对回潮水分的影响试验数据。
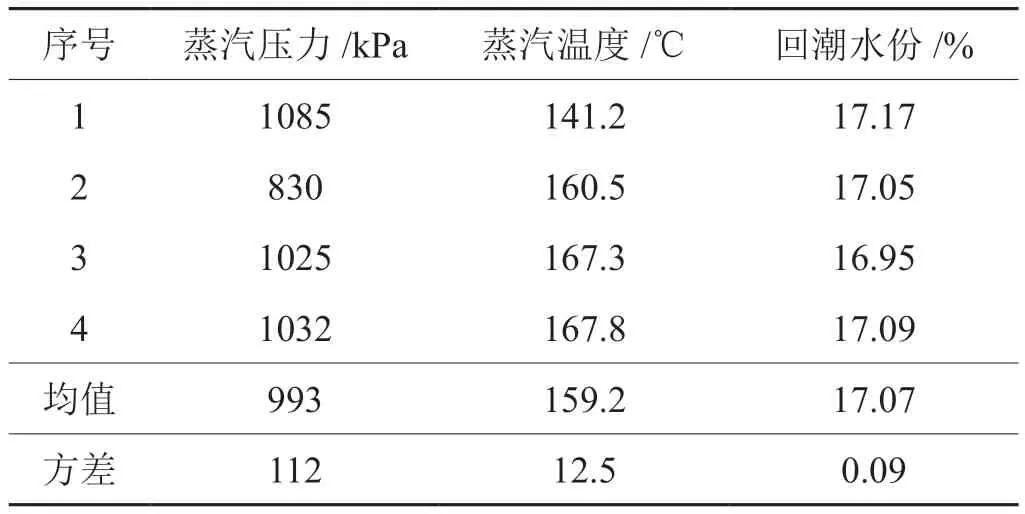
表2 蒸汽变化对回潮水分的影响试验数据表Tab.2 Moisture affected by steam
由表2数据可见,尽管蒸汽压力由830kPa变化到1085kPa、温度由141℃到168℃,但是,回潮水分受影响在±0.5之内。在允许范围内,可认为不受影响。
3.1.2 装烟重量变化的影响
烟包切3刀分4片后装框,将导致装烟重量发生变化,有必要试验装烟重量变化对回潮水分的影响。
由表3数据可见,装烟重量变化了5kg(25%),对回潮水份的影响不显著。
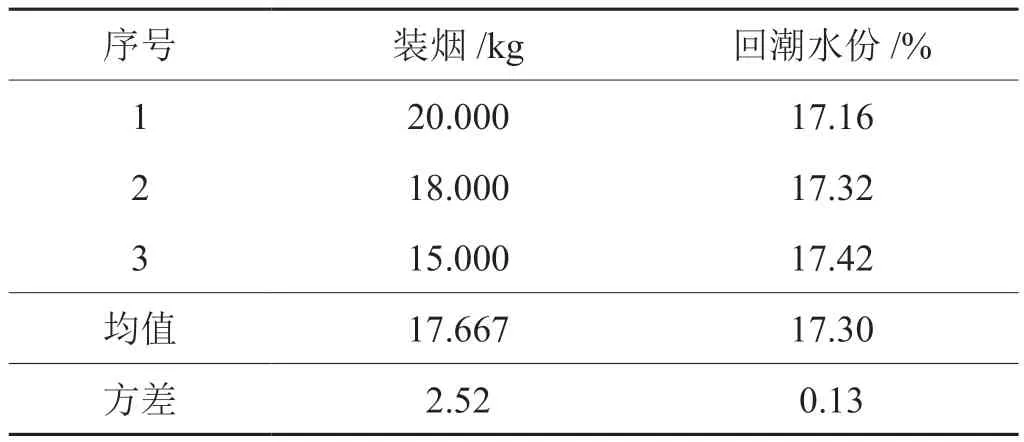
表3 装烟重量变化对回潮水分的影响试验数据表Tab.3 Moisture affected by the weight of cigarette packed
3.1.3 装烟水份变化的影响
烟包在库房保存3年以上,通风、气温和湿度不同,导致来料水分不同,有必要试验来料水分变化对回潮水分的影响。
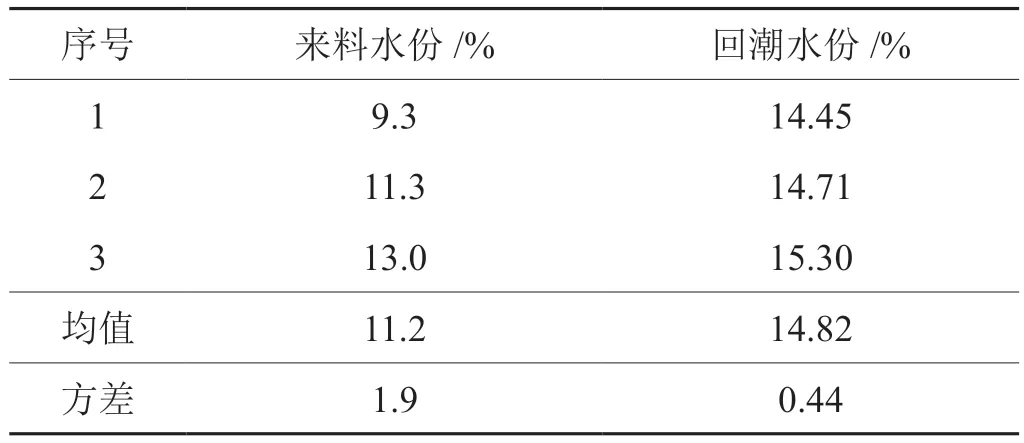
表4 来料水分变化对回潮水分的影响试验数据表Tab.4 Moisture affected by humidification of cigarette material
由表4数据可见,来料水分从9.3%变化到13.0%,回潮水份所受影响不显著。
3.1.4 环境温度的影响
室内温度也会变化,表5示出室温变化对烟包水分的影响试验。
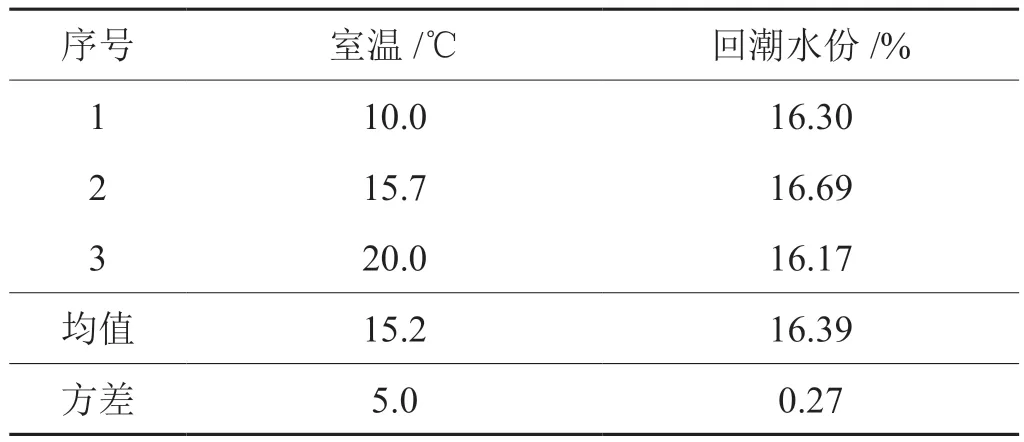
表5 室温变化对回潮水分的影响试验数据表Tab.5 Moisture affected by room temperature
由表5数据可见,室温从10℃变化到20℃,回潮水分不受影响。
3.1.5 试验分析
由于参考模型的输出不受蒸汽温度和压力、装烟重量和环境温度等的影响,采用积分控制后,回潮机要按参考模型工作,所以回潮机的出口水份也不受这些因素的影响。
为了更真实地反映实际情况,表2~表5所对应的出口水分设定值不同,设定值表2和表3为17、表4为15、表5为16,由表中的水分均值与设定值对比,可见,差值并不大,误差在允许范围内。
3.2 回潮水分可设定
表2~表5水分均值随设定值而改变,为直观起见,表6专门给出回潮水份与设定值的试验数据,由数据可见,回潮水分与设定水分之间的误差在±0.5之内。

表6 回潮水分与设定值间的试验数据Tab.6 Data of measured moisture affected by given
3.3 回潮水分明显增加
从表2~表6和更多的试验数据可见,在烟包(也称作包心)温度不超过70℃、出口水分不大于16%的条件下,能够增加水分6%,明显高于现有2%的水平。
由于回潮机在积分控制下按参考模型工作,而参考模型又是AI训练后寻优的结果,水份增加被最大化,而现有真空回潮的能力不足,所以,比较而言新控制下水份增加明显。
4 结语
本文针对真空回潮实验机,根据输入输出数据构建了机内压力和温度、烟包水分和温度等状态量的稳态模型和动态模型,解决了箱内温度、压力分布不均匀和烟包温度与水分不可测的难题,观测到了真空回潮机的状态量。试验检验表明机内压力和温度的模型误差在1%之内,烟包温度误差在2%之内,烟包水分的误差在0.5%之内。
通过仿真训练,由AI算法找到回潮时间约束条件下的水份最大化的参考模型;最后采用参考模型法,通过积分控制,让回潮机的状态量跟踪参考模型的状态量。
试验数据表明,设计的回潮控制能够①提高回潮能力,包心温度不超过70℃下,增加水份从2%提高到6%,出口水份达到16%;②提高回潮水份的一致性,回潮水份不再受蒸汽温度和压力、烟包等级和水份与重量、环境温度等因素变化的影响;③回潮水份还能够提前给定,出口水份与设定值的误差在±0.5%之内。
本文理论与试验充分体现了真空回潮在建模后可观、控制后工艺指标精准,体现了智能特点。
要保证回潮水份的一致性,需要事先知道来料水份,因此建议安装烟包水份在线测试仪。
本文试验还不够全面,河北中烟已要求保定卷烟厂质量工艺部对实验机进行试验并出具试验报告,结果将另文发表;建模控制还能提高真空回潮的回透率,但所用模型和控制都与本文不同,日后再另文介绍。
致谢 本文作者特别感谢河北中烟公司提供试验用烟和试验场地。
