锂离子电池正极材料Li2FeO2的电子结构性质和Li扩散*

林传金 郑锋 朱梓忠†

1)(闽南师范大学物理与信息工程学院,漳州 363000)

2)(厦门大学物理科学与技术学院,九江研究院,厦门 361005)

1 引 言

目前,Li离子电池已经在便携式电子设备上得到了广泛的应用[1].但是,在把锂离子电池用到全电动汽车上时,能量密度和安全性成为制约电动汽车电池发展的重要因素[2].全固态锂离子电池的发展是一个重要方向[3,4].为了开发全固态锂离子电池,就要求电极材料具有较高的能量密度和锂离子导电性.现阶段,对锂离子导电性的研究具有重要的意义.在过渡金属中,Fe在自然界中非常丰富并且无毒,所以Fe基锂离子电池一直是研究的热点,主要涉及以下几个体系:LiFeO2,LiFePO4,Li2FeSiO4等[5].相对而言,LiFeO2具有更小的分子量,理论上可以获得更高的比容量.鉴于岩盐结构的LiCoO2具有优秀的电化学性能,具有相似结构的LiFeO2也受到广泛的关注[6].目前实验上能合成的LiFeO2多达10种晶型,但是电化学实验结果表明它们的实际容量都不是很高.为了提高它们的电化学性能,还必须采用掺杂或纳米化等手段[7].另外,为了进一步提高LiFeO2类材料的比容量,基于 LiFeO2体系,可以构造 Li2FeO2分子式的材料.由于Li2FeO2分子式比LiFeO2多一个Li,可以增加每分子的含Li量,因此就增加了每个分子可脱嵌Li的量,理论上就可以大幅度地增加比容量.在合成的Immm结构的 Li2CuO2[8,9],Li2NiO2[10−12]和 Li2CuxNi1–xO2[13]材料中发现,此类材料不仅具有较高的比容量,而且有更低的Li离子扩散势垒.目前关于Immm结构的Li2FeO2在实验上还没有相关的报道.本文从理论上研究这种材料不仅可以进一步丰富对此类材料性质的认识,而且对这类材料的探索及材料性质的预测具有重要的意义.

2 计算方法

本文的计算基于密度泛函理论(density functional theory,DFT)的第一性原理方法,采用VASP程序包,交换关联能采用广义梯度近似(generalized gradient approximation,GGA)[14],采用了Perdew-Burke-Ernzerhof表达式[15].电子与离子间的相互作用使用投影缀加波(projected augmented wave,PAW)方法来描述[16].电子波函数用平面波基组展开,平面波截断动能为500 eV.系统总能量的收敛标准为 1×10–5eV/atom.结构优化和电子结构计算时的布里渊区积分采用了Monkhorst-Pack方法[17],使用了8×8×8以G为中心的特殊k网格点.用 DFT+U[18]的方法处理电子有局域化特征的铁离子的d电子,等效势Ueff的值取4.3 eV[19].计算Li离子的迁移路径和迁移势垒时,运用 CI-NEB(climbing image nudged elastic band method)方法[20]进行计算.为了避免由于采取了周期性条件使得迁移的锂离子之间存在相互作用,NEB 计算采用了 3×3×1的超原胞(包含18个Li2FeO2分子式单元),采用这样的超晶胞可以使相邻原胞的迁移锂离子间的距离保持在8 Å以上,并且在所有的迁移势垒计算时都可以采用单个锂空位的条件,即保持35个Li和一个空位的比例浓度,因此能保证计算的准确性.对于超晶胞的计算,布里渊区积分采用了Monkhorst-Pack 方法产生的 2×2×2 以G为中心的特殊k网格点.关于体系中含有过渡金属d电子时扩散势垒的计算,Morgan等[21]对Li扩散势垒的计算认为,GGA+U方法在计算锂离子迁移势垒时会高估离子的迁移势垒(掺入了电子迁移的势垒).如果只采用GGA的方式,电子将会是更加非定域的[22],从而减少电子-空穴相互作用对跃迁势垒计算的影响,本文的计算结果也符合他们的分析.关于d电子的计算是否加U应根据具体的情况来定,如Zhao等[23−25]在处理Pb基钙钛矿时只用了GGA处理d电子就可以得到比较好的结果.本文也采用 GGA 近似计算 Li2MO2(M=Fe,Co,Ni,Cu)的不同路径的扩散势垒.但是为了对比GGA和GGA+U对迁移势垒的影响,我们在同样精度条件下分别计算了Li2NiO2在不同迁移路径下的扩散势垒,如表1所列.从表1可以看出,采用GGA+U计算的扩散势垒比GGA结果大一些.

表1 GGA 和 GGA+U 下 Li2NiO2 的扩散势垒Table 1. Li2NiO2 diffusion barriers under GGA and GGA+U.

3 结果与讨论

本文讨论的Li2FeO2材料属于斜方晶系,空间群为Immm,标记为Immm-Li2FeO2.电子结构和电荷密度计算时采用了Li2FeO2原胞,但是在计算Li离子的迁移路径和迁移势垒时,采用了3×3×1的 Li2FeO2超原胞(包含了 18个 Li2FeO2的分子式单元),如图1所示,采用这样的超原胞可以使相邻周期内的迁移的锂离子间距离保持在8 Å以上.图1的结构和对称性显示,沿c轴方向,O原子呈4边形非紧密排列,排列形成的O原子面沿c轴方向呈 AABB··堆积.Fe 原子位于 O 原子构成的AA或BB面之间,而且Fe周围2个氧在上另2个氧在下而组成O原子的正方形,Fe就在其中心处,也在相邻的AB或BA之间.Li占据O四面体的中心,形成FeO4正方形与LiO4四面体沿c轴方向层状交替排列.

图1 Immm-Li2FeO2的 3×3×1 超原胞及 Li迁移路径示意图Fig.1.The 3×3×1 supercell and the Li migration paths of Immm-Li2FeO2.

由于目前还没有实验合成Immm-Li2FeO2材料的报道,可以先通过理论计算预测此种材料的结构稳定性.计算了Immm-Li2FeO2的声子谱,如图2所示.可以看出,声子谱没有存在虚频,由此可预测Immm-Li2FeO2结构是稳定的,在未来的实验中有可能合成.

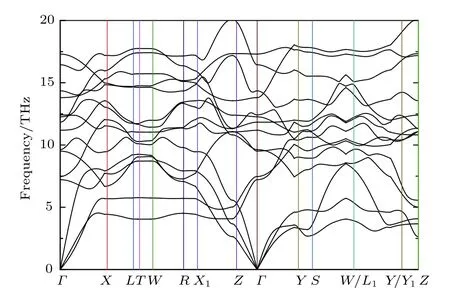
图2 Immm-Li2FeO2 的声子谱Fig.2.Phonon-dispersions of Immm-Li2FeO2.

不仅对晶胞结构参数进行了优化,而且对晶胞内的原子位置也进行了充分的弛豫.计算得到的结构参数如表2所列,与计算得到的同样结构的Li2CuO2[9]和 Li2NiO2[11]对比,Li2FeO2中的 Fe2+半径(0.77 Å)大于 Cu2+的半径(0.71 Å)而且大于 Ni2+的半径(0.69 Å)[26].三种金属离子 Fe2+,Cu2+和Ni2+均与O配位形成正方形结构.同样的配位场与相同的离子价态下,离子的半径越大,所对应的晶胞体积越大.从表2可以看出,本文计算的结果符合这个规律.通过计算的键长发现,Fe—O键长均为2.010 Å(Fe与O组成FeO4正方形),而 Li—O 有两种键长,与 Fe 原子正对的 Li所对应的 Li—O键长为 2.016 Å,大于与 Fe不正对的 Li的 Li—O 键 长(1.954 Å).这 是 因 为 Li与O组成LiO4四面体结构,沿c轴方向,其中2个O在A面,2个O在B面,所以形成了不等长的Li—O 键.

为了了解Immm-Li2FeO2材料中电子排布以及电子成键的特征,图3和图4给出了面的总电荷密度以及差分电荷密度的分布情况.差分电荷密度定义为:其中ρ(r)是 体系的总电荷密度,是体系中所有独立原子电荷密度的叠加.从图3可以看出,Immm-Li2FeO2材料的键合特征表现为离子性和共价性的混合,而且离子性给出了成键的主要部分(电荷的球形分布体现了离子性,而偏离球形分布的部分体现了共价性).从图4可以看出,Fe-O间的电荷转移比较明显(O明显得到电子),而且Fe周围电荷密度重新分布的情形非常明显.这也再次体现了该材料中电子键合的主要特点是离子性和共价性的混合.图4也显示了Li上的电子完全消失,这与我们的预期是一致的.

由于铁基材料经常呈现铁磁或反铁磁性,因此首先计算了铁磁和反铁磁情况下Immm-Li2FeO2材料的总能.计算结果显示,铁磁情况下Li2FeO2的总能略低于反铁磁情况下的总能,因此在余下的对Li2FeO2材料的计算中均只考虑铁磁的情况(考虑了自旋极化效应).根据晶体场理论,平面正方形配位的Fe2+离子的d电子能级将分裂为(能量由高到低)dx2−y2,dxy,dz2和 2 度简并的 dxz,dyz能级.Immm-Li2FeO2材料中为二价铁Fe2+,有6个未饱和的3d电子,铁离子的核外电子排布有高自旋、低自旋和非自旋3种排布方式.由洪德理论可知,铁离子Fe2+核外的6个d电子在高自旋的分布中有5个电子先分别排布5个分裂轨道的自旋向上的能级,而另一个则填在dxz或dyz轨道的自旋向下的能级,此时 Fe2+的磁矩为+4(单位为 μB,下同);在低自旋情况下,4个电子先填满dxz和dyz轨道,另2个电子分别排布在dz2和dxy的自旋向上的能级上,此时Fe2+的磁矩为+2;非自旋情况下,6个电子填满dxz,dyz和dz2的自旋向上和向下轨道,此时Fe2+的磁矩为0.关于晶体配位场作用下,过渡金属离子d电子不同自旋态的讨论与计算已经有一定的报道[27],本文采用同样的方法,表3列出了这3种电子组态情况下的磁矩和总能,计算得到的高自旋情况下Fe2+的磁矩为3.923,低自旋情况下Fe2+的磁矩为2.014,计算的结果与上面的分析相符.从计算的总结合能结果可以看出,高自旋与低自旋情况下Li2FeO2材料的总能较低,而且低自旋情况下的能量最低(比高自旋的能量还低0.063 eV).鉴于低自旋组态具有最低的总能,电子结构的计算将采用低自旋的电子排布.

表2 Immm-Li2FeO2 的结构参数与键长Table 2. Structural parameters and the bond lengths of Immm-Li2FeO2.

图3 Li2FeO2( 11)面的总电荷密度图Fig.3.Total charge densities of Li2FeO2( 11).

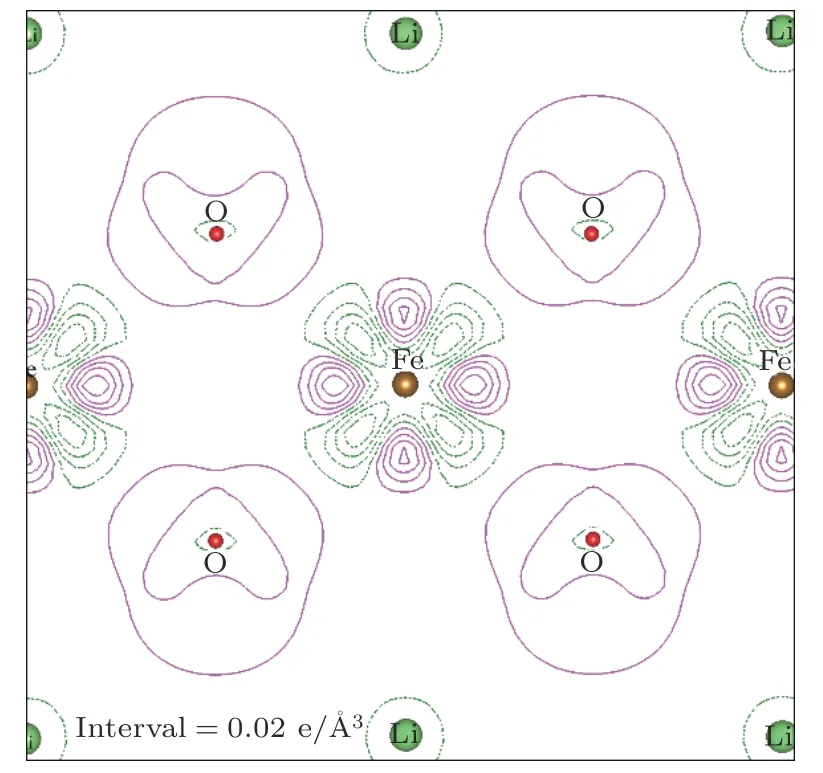
图4 Li2FeO2( 11)面的差分电荷密度图Fig.4.Deformation charge densities of Li2FeO2( 11).

表3 不同电子自旋组态的 Li2FeO2 的总结合能与Fe2+磁矩Table 3. Total cohesive energies and magnetic moments under different spin configurations of Li2FeO2.

图5(a)和图5(b)分别给出了计算得到的Li2FeO2材料的自旋向上和自旋向下的能带结构图,图6是计算得到的Li2FeO2材料的总态密度图以及 O2s,O2p轨道和 Fe4s,Fe3d轨道的自旋向上和自旋向下的分波态密度图.Li+处于离子状态,电子态密度很小,故没有给出.通过能带结构图可以看出,Immm-Li2FeO2材料具有“半金属”的特征(half-metal,下面进一步讨论).从分波态密度图可以看出,自旋向上能带的价带顶主要由O2p和Fe3d所贡献,导带底则主要由Fe3d,O2p和O2s所贡献.另一方面,计算结果也显示,自旋向下能带的费米面附近的状态并非全部是d-电子态,而是Fe-3d 电子和 O-2p 电子的杂化态.dz2,dxy的能带是小部分被占据的,而2py,2pz的能带则是小部分非占据的,从而使得自旋向下的能带是金属性的,也最终导致低自旋态的Li2FeO2是半金属性的(即half-metal).

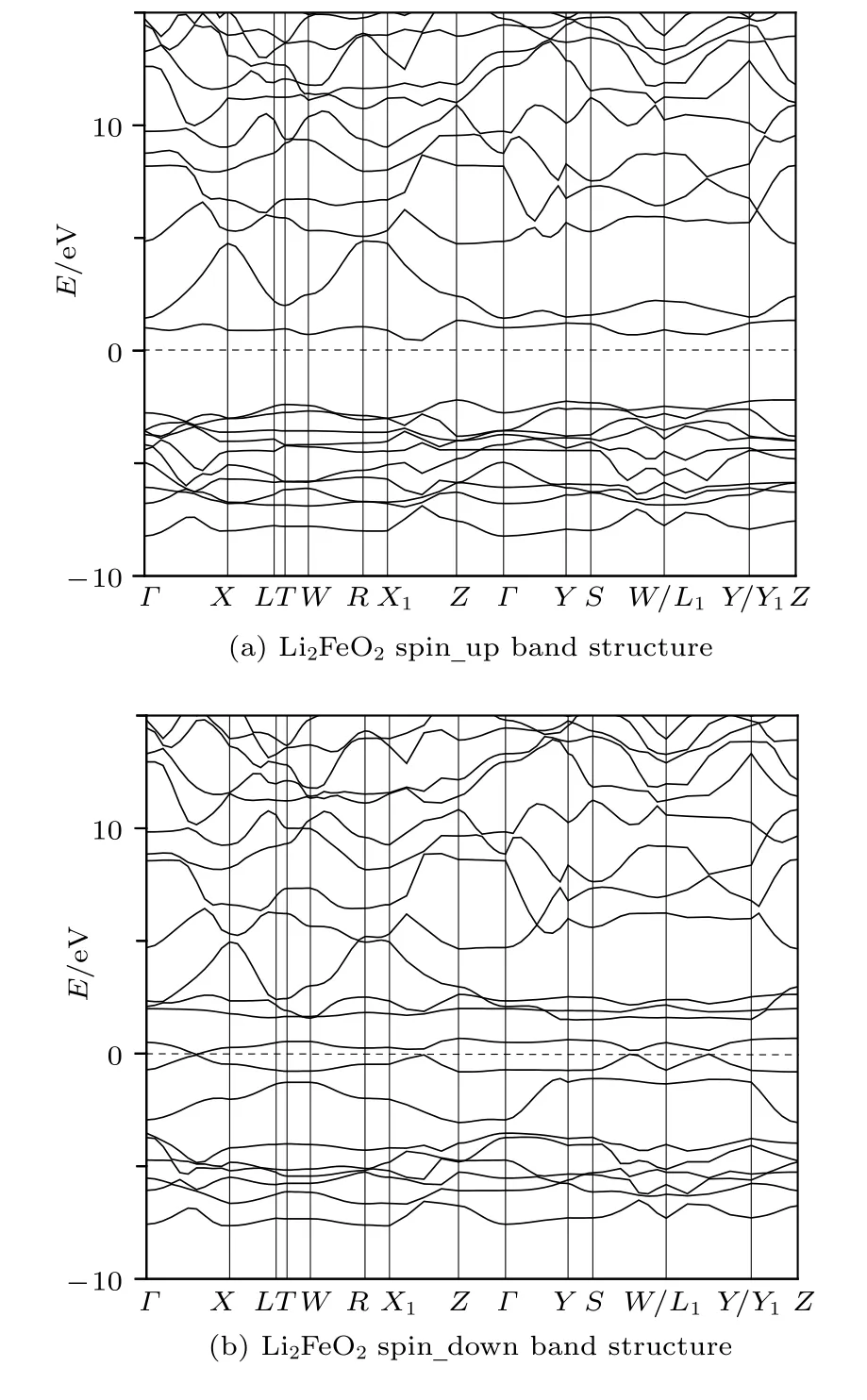
图5 Li2FeO2 自旋向上(a)和自旋向下(b)的能带结构图Fig.5.(a)Spin-up and(b)spin-down band structures of Li2FeO2.

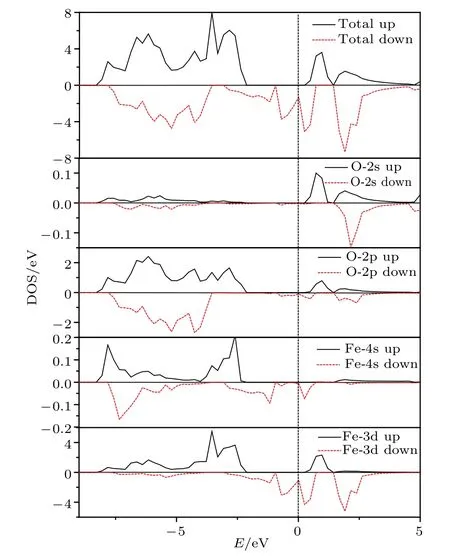
图6 Li2FeO2 的总态密度和 O,Fe 的分波态密度图Fig.6.Total density of states(DOS)of Li2FeO2 and partial density of states of O and Fe.

对比自旋向上和自旋向下的能带结构图可以发现,Immm-Li2FeO2材料呈现半金属的特征.这是因为自旋向上的能带存在带隙,表明自旋向上的Li2FeO2呈现半导体属性,而自旋向下的能带图中费米能级穿过能带,表明此时的Li2FeO2呈现金属的性质,从而使得Immm-Li2FeO2有 halfmetal的特质(区别于semi-metal时的半金属特征).从磁学的角度,可以使用费米能级上自旋向上的状态密度(N↑(EF))与自旋向下的状态密度(N↓(EF))的差来表征材料的自旋极化程度,即自旋极化率通过对Li2FeO2电子结构的计算,Li2FeO2自旋极化率P=8.01%,说明 Li2FeO2呈现出比较弱的自旋极化.但是对比半导体性的正极材料,Li2FeO2材料还是有更好的电导率.

为了研究锂离子Li+在Immm-Li2FeO2材料中的扩散情况,使用CI-NEB方法[20]对几条Li+的迁移路径进行了计算.图1中标出了Li+分别沿a,b,c方向和ab对角方向的4条可能的扩散路径.1)Path A:Li+沿图1中a轴方向迁移的路径.2)Path B:Li+沿图1中b轴方向迁移的路径.Li+离子沿此方向迁移时,需要从一个O原子的四面体中心迁移到下一个四面体的中心.沿这个方向扩散还要直接跨过FeO4面,所以Li+的迁移将受到Fe离子较强的排斥作用.Kang等[11]在研究Li2NiO2中Li+离子沿此路径迁移时,发现势垒高度是沿a轴迁移的势垒大小的5倍多,因此他们认为Li+离子沿这条路径迁移是不可能的.对此,本文没有计算沿此方向路径的迁移.3)Path C:沿图1中c轴方向迁移的路径.4)Path AB:沿ab轴对角方向迁移的路径.此路径中,Li+离子沿ab轴方向迁移,Li+离子从一个四面体中心跳到相邻的锂空位四面体中心.

根据以上分析,选择了3条Li离子可能扩散的路径(path A,path AB,path C)进行计算.除了考虑Immm-Li2FeO2材料,还对比研究了同样的Immm结构的其他过渡金属正极材料Li2MO2(M=Co,Ni,Cu),对这 4 种材料进行的 Li离子扩散势垒的计算结果如表4和图7所示.可以看出,Li2FeO2在所有这些体系中,在各扩散路径上都有最小的跃迁势垒.

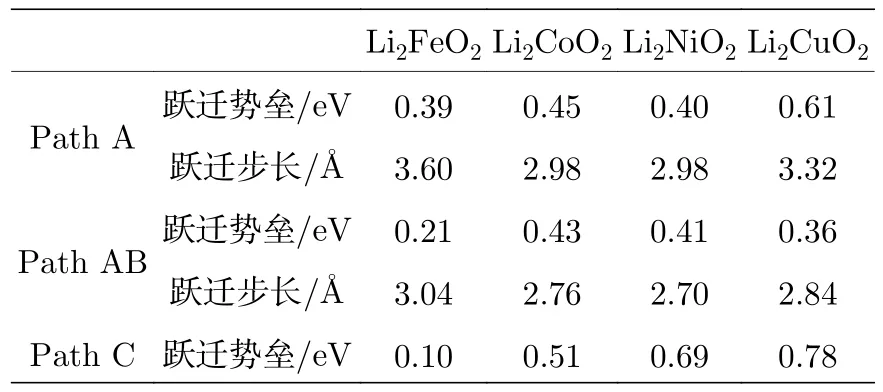
表4 不同跃迁路径的 Li2MO2 (M=Fe,Co,Ni,Cu)的跃迁势垒与跃迁步长Table 4. Energy barriers and distance for different Li+ migration paths in Li2FeO2.

图7(a)是计算得到的迁移路径和相应的势垒图.从图7(a)可知,Li2FeO2材料中 Li+离子沿Path A迁移到下一个Li空位时,其迁移势垒为0.39 eV,迁移步长为 3.60 Å.沿ab轴的对角方向迁移时,计算的迁移路径和势垒的关系如图7(b)所示.从图7(b)可以看出,沿此方向(Path AB)迁移时,迁移势垒为 0.21 eV,迁移步长为 3.04 Å.当沿c轴方向迁移时(Path C),虽然Li+离子无法穿过Fe2+层并且一直沿c轴方向迁移,但是Li+离子还是有可能先从初态P1位置迁移到对面的末态P2位置,然后再沿其他方向迁移,因此也有必要计算沿c轴方向Li层之间的Li+离子迁移,图7(c)就是计算所得的迁移路径与势垒高度的关系,即势垒为 0.1 eV,跃迁步长为 4.32 Å.综上所述,对于Immm-Li2FeO2材料,沿c轴方向相邻的 LiO4层之间的Li离子迁移具有最小的迁移势垒.虽然Li+离子很容易在此相邻的层间迁移,但是继续沿c轴方向的迁移将遭遇FeO4层,Li+离子就无法继续沿c轴扩散.由于沿ab轴对角方向的扩散势垒(0.21 eV)小于沿a轴方向的势垒(0.39 eV),所以沿ab轴对角方向的扩散是最容易发生的Li+离子迁移.这个结果与文献 [9,11]研究的 Li2CuO2和Li2NiO2对应的Li+离子迁移的情况相一致.本文中,即便是锂离子扩散路径上的最大Li+离子迁移势垒(0.39 eV),也比已有的Fe基Li+离子正极材料Li2FePO4[29,30]和Li2FeSiO4[31]具有更低的扩散势垒.这意味着Li2FeO2中的Li+离子将有更高的扩散系数,这对于Li2FeO2材料作为正极材料具有重要的意义.利用Li+离子沿某一路径的迁移步长和所遇到的迁移势垒,可以估算出Li+离子沿该路径的扩散系数:D=d2v·e xp(−EA/kBT)[32,33],式中d为迁移的距离,v为尝试频率(即晶格振动的频率,一般可取为 1013Hz),EA为势垒高度,kB为玻尔兹曼常数,T为温度.根据本文计算结果,可以算出Li+离子分别沿ab轴对角方向和沿a轴方向迁移时的扩散系数随温度的变化,结果如图8所示.从图8可以看出,Li+离子沿ab轴对角方向的扩散系数远大于沿a轴方向的扩散系数(因为沿a轴方向迁移的势垒大于沿ab轴对角方向的迁移势垒).室温附近(300 K),沿ab轴对角方向的扩散系数约为 1.34×10–5cm2/s,而沿a轴方向的扩散系数则只有 1.81×10–8cm2/s.随着温度的增加,扩散系数的增加有一定的“增速”,但是增加的不是很大.

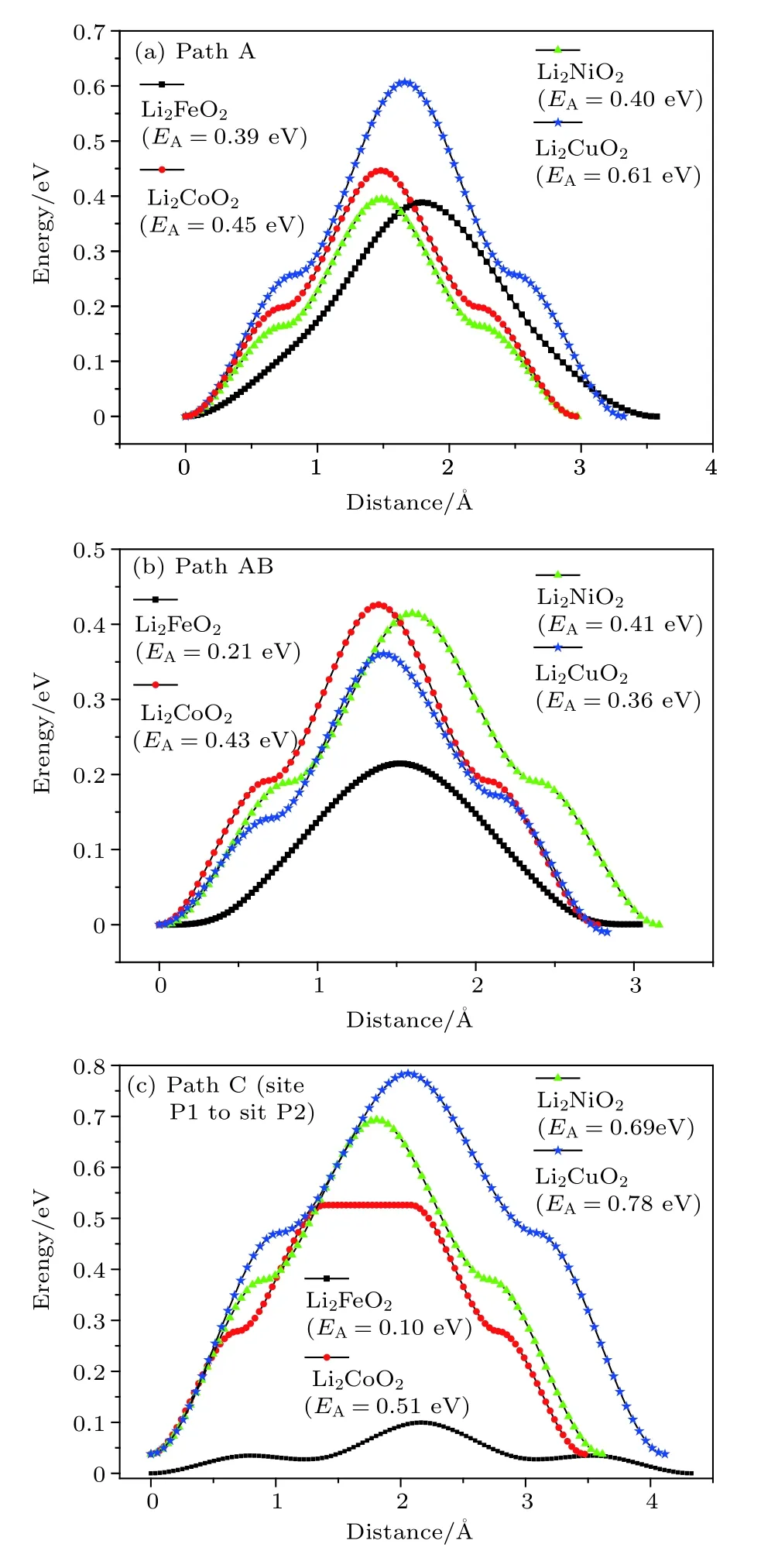
图7 Li2MO2(M=Fe,Co,Ni,Cu)中 Li+离子不同迁移路径的势垒(a)Path A;(b)path AB;(c)path C(P1—P2)Fig.7.Energy barriers for different Li+ migration paths in Li2MO2(M=Fe,Co,Ni,Cu):(a)Path A;(b)path AB;(c)path C(P1–P2).

图8 Li2FeO2 中(a)path AB 和(b)path A 方向 Li+离子扩散系数随温度的变化Fig.8.Temperature dependence of Li ion diffusion coefficients along(a)path AB and(b)path A in Li2FeO2.

4 结 论

本文采用基于DFT的第一性原理方法计算了锂离子电池正极材料Li2FeO2的声子谱、电子结构和Li+离子的迁移路径及扩散系数,并与其他同样结构的 Li2CoO2,Li2NiO2,Li2CuO2进行了对比.结果发现,Immm-Li2FeO2材料具有结构稳定性,呈铁磁性,Fe2+外层d电子更容易处于低自旋态,自旋极化P=8.01%.从能带结构可以看出,Immm-Li2FeO2具有“半金属”材料的特征,计算的自旋向上的能带表现为间接带隙的半导体,带隙为 2.61 eV,自旋向下的能带表现出金属特性.假设Li离子沿最近邻的空位进行扩散,我们计算并分析了4条Li+离子迁移路径的扩散势垒,结果显示:Li+离子在c轴方向Li层之间的迁移具有最小的势垒,迁移势垒为 0.1 eV;沿ab轴方向迁移的势垒为0.21 eV;而沿a轴方向迁移的势垒为0.39 eV.这些势垒比 Li2CoO2,Li2NiO2,Li2CuO2材料中计算的势垒小,也比已有报道的其他Fe基Li+离子正极材料的Li迁移势垒更低,意味着对Immm-Li2FeO2材料的研究具有重要的意义.此外,沿Path AB 路径的扩散系数约为 1.34×10–5cm2/s,远远大于沿Path A路径的扩散系数,约为1.81×10–8cm2/s.