井下超声流量计的误差分析
2019-09-03林龙贵
林龙贵
(贵州航天控制技术有限公司,贵阳550009)
1 引言
在贵州航天控制技术有限公司的井下超声流量计开发成功之前,油田使用的流量计主要由浮子式、涡轮式、电磁式等几种原理制造的产品,由于受井内原油、泥沙和液体黏度的影响,这些流量计的测试精度和可靠性都较差。井下超声流量计从原理上解决了粘度法测定聚合物流量的测试问题。
2 随机误差分析
随机误差是产品在相同条件下,多次重复测量同一物理量时,误差值呈无规律变化的一种误差,随机误差不能用实验方法消除,也不能修正,只能依靠统计规律了解其分布特性[1]。
2.1 流量微分方程
流量公式:
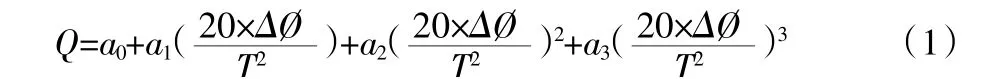
得全微分方程:
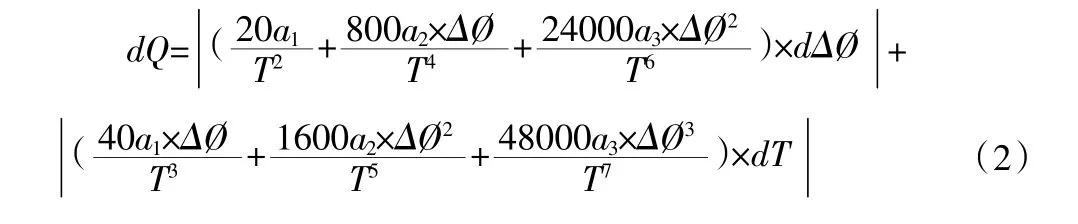
式中:
a0、a1、a2、a3——流量标定系数,(无量纲);
T——超声波传播0.2m 所用的时间,(μs);
ΔØ——超声波在顺流、逆流中传播0.2m 产生的相位差。
在式(2)中,由于dΔØ 和dT 的变化是随机的(统计符合正态分布),所以两部分的误差取绝对值之和。
2.2 随机误差计算
对测试的数据进行统计后,得出了在同一条件下的流量测试的原始数据,其传播时间“T”随机变化dT=1~2μs,相位“ΔØ”随机变化dΔØ=10~20 个A/D 采集位,由于“T”和“ΔØ”的随机变化,导致了在同一条件下的流量Q 的随机变化。
在以下的误差计算中,设T=134μs(多数仪器测试的时间“T”为130μs-140μs=134μs),dT=1μs,dΔØ=10(针对多数仪器的dT、dΔØ 的变化范围),带入式(2)得:
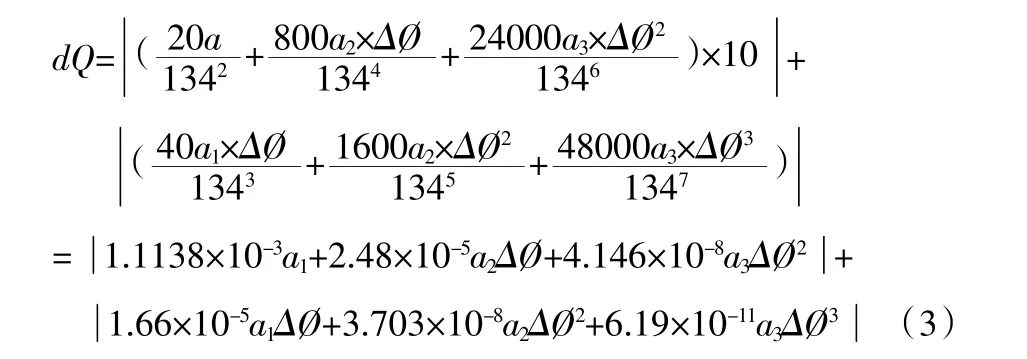
式(3)即为随机误差估算公式。
3“相位法”误差分析
3.1 原理误差分析
在实际测试中,如果水温较高、压力较大,则声速“c”变大、时间“T”变小;又根据“可知,“”,此式说明流量Q 的自变量“不受声速“c”的影响;但在相位法测试中,仪器只测试其相位“ΔØ”随声速“c”的变化(原理上“ΔØ”与“c2”成反比,“T2”成正比),忽略其时间“T”随声速“c”的变化,从而使“”与声速“c”成反比,进而使Q 流量与声速“c2”成反比,这是相位法测试中产生的原理误差,即在高温、高压环境中实测的流量Q 会比真实流量小(即Q实测≤Q真值)。
3.2 原理误差估算
在误差估算中,取时间T2=1000(这是相位法计算中给定的值),声速c 从1480~1555m/s,即水温从20~70℃时声速的变化(没有考虑压力对声速c 的影响)。则:
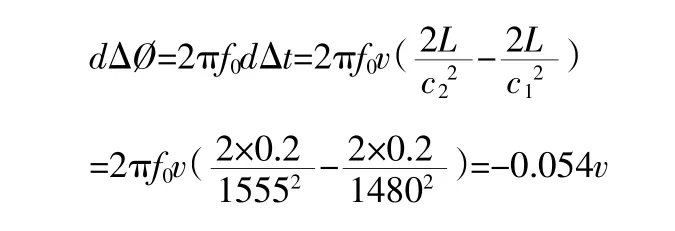
将dΔØ 变成A/D 采集值:
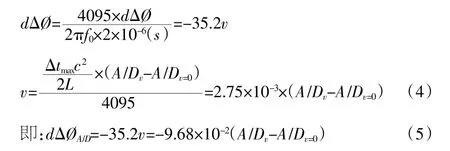
式(4)(5)中:
dΔØA/D——dΔØ 的A/D 采集值;
A/Dv=0——流速为“0”时的A/D 采集值;
A/Dv——流速为“v”时的A/D 采集值;当v=0 时,A/Dv=A/Dv=0。
在式(8)中,Δt 取2μs(即2μs 所产生的相位的A/Dv采集值为4095),c 取1500m/s,式(5)中的“-”号表示当声速“c”变大时,相位的A/D 采集值变小,即实测流量变小。
又根据相位法求流量的公式:
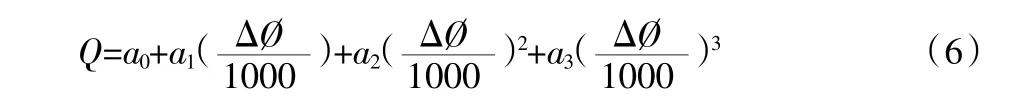
得相位法误差公式:
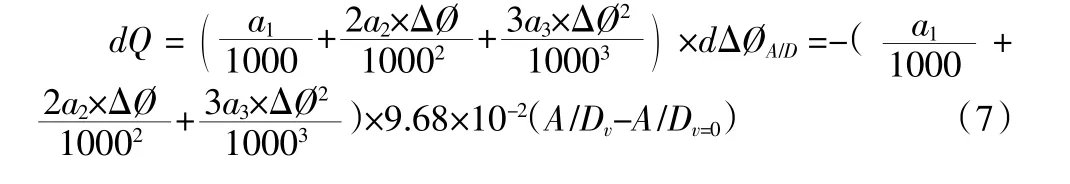
4“相位-时间法”误差分析
根据式(1),考虑到ΔØ 和“T”的综合影响,求全微分方程为:
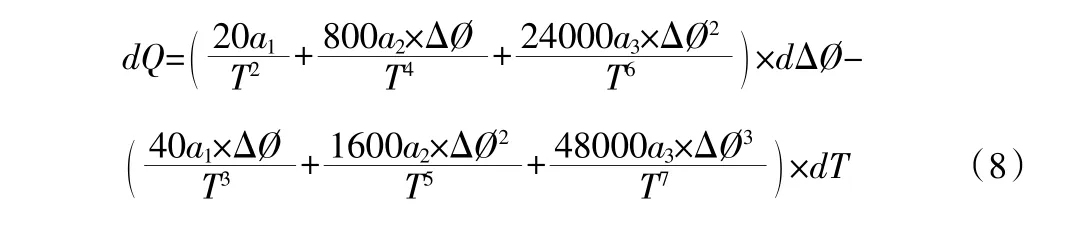
此式与式(2)的区别在于没有绝对值符号,这给两部分误差的相互抵消带来了可能。
当声速“c”从1480m/s 变到1555m/s 时,dΔØA/D(max)的表达式和式(5)一样,即:dΔØA/D=-35.2v=-9.68×10-2(A/Dv-A/Dv=0);
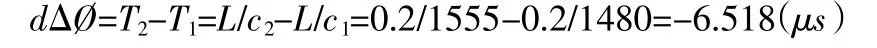
在式(8)中,取T=134μs,结合上两式得:
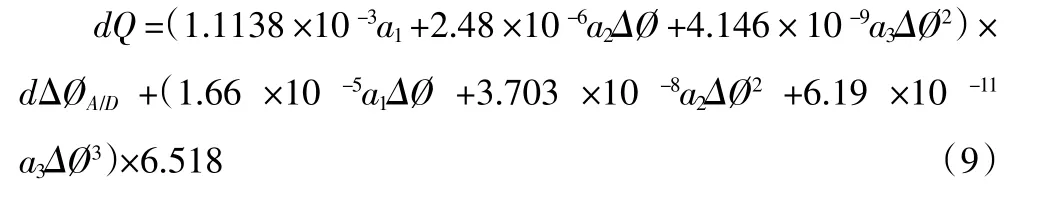
式(9)即为“相位-时间法”在声速“c”从1480m/s 变到1555m/s 时的误差估算公式。
5 误差的验证
5.1 随机误差估算的验证
统计出04A057 号仪器的相位ΔØmax=800,带入式(3)得:
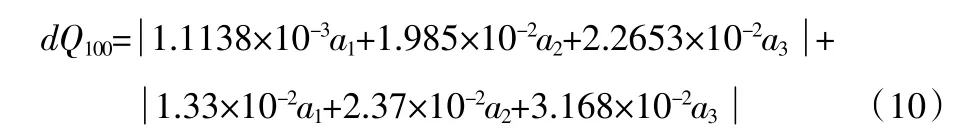
对04A057 号仪器的标定(标定精度为1.74%)得:
a1=126.58903,a2=8.71896,a3=-5.56843 代入式(10)得:dQ100=0.166+1.71=1.876(m3/d),即随机相对误差=1.88%。
在随机误差估算中,流量误差的产生由两部分组成:即由“dΔØ”产生的相位测试误差和由“dT”产生的时间测试误差之和。从A-100m3/d、A-200m3/d、A-300m3/d 的标定数据看:相位测试误差的绝对值比较小(均在1m3/d 以下)、而时间测试误差的绝对值随量程的增大而增大,相对误差之和随量程的增大而减小,但最大不大于3%(F·S)。
根据误差分配原则+,在温度、压力变化不大的情况下,采用相位法(x 法)克服了“dT”的影响,即排除了时间测试误差,所以更容易标检合格。
以上随机误差的大小依赖于仪器的测试精度和换能器的稳定度。
根据误差理论,该随机误差遵循正态分布,并且可针对具体的流量台阶的多次测试数据计算出特定流量条件下的标准偏差“σ”及精密度指数“h”。由于随机误差的概率密度分布函数计算需要依靠大量的统计数据才能保证其准确性,统计和计算的工作量大,故忽略此环节。
5.2 相位法误差估算的验证
以下验证中的方程形式为:Q=a3x3+a2x2+a1x+a0,其中x=ΔØ/1000,ΔØ 为相位的“A/D”采集值(即ΔØ=A/Dv)。
对03A052 号仪器进行相位标定得实际拟合方程:
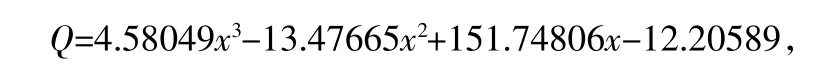
取A/Dv=794(实测最大值),A/Dv=0=80(实测零位),则由式(5)得:dΔØA/D(max)=-9.68×10-2×714=69.12,将dΔØA/D(max)代入式(7)得:
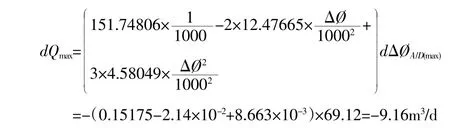
即声速在1480~1555m/s 时产生的相对误差为:
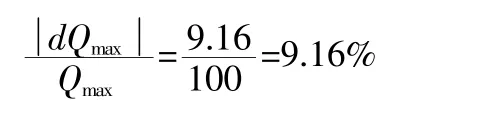
从上看出,当声速“c”从1480m/s 变到1555m/s(即水温从20℃变到70℃)时,相同的实际流量,测试时可差10%左右,反映到实际生产过程中,超差的仪器大部分出现在水温变化较大的时候。
6 结论
依据对流量计存在的随机误差、“相位法”误差和“相位-时间法”误差的分析结果,结合流量计目前的技术水平,可以认为:
①随机误差是暂时无法消除的(误差一般在2%~4%左右),它主要由换能器决定,这也是造成流量标定精度较高、而检定精度较低;或流量标定精度较低、而检定精度较高的主要原因;
②“相位法”误差属于原理性误差。当工作环境变化较大时会产生较大的误差,如果考虑压力的影响,则误差将会更大;
③“相位-时间法”误差也属于原理性误差。主要由电路产生的相位零位引起,因为相位零位是流速=0m/s 时的相位,由此看见,从原理上就把相位分成了两部分:固定相位,和流速相位,相位本来随声速“”变化,样这一来,为常数的“固定相位”和“流速相位”一起变成了自变量。目前,生产的流量计的设计零相位均在70~150 个A/D 值左右,所以由于零相位带来的误差均在2m3/d 左右。
消除“相位-时间法”误差的办法是在拟合方程时减去零相位,这一点在以后的计算中可以进一步完善。
综上所述,可以得出两条结论:
第一,在今后的流量标检中,只能采用“相位-时间法”;第二,随机误差遵循正态分布,且主要受测试时间“”的影响,所以,在仪器标检超差(超差幅度为:4%以内)的情况下,可以将上下换能器对换后重新标检,但超差大于4%时要另找其他的原因。
