金属低周疲劳过程热力学熵特征分析及寿命预测模型

朱达荣 徐德军 刘 涛 汪方斌 储朱涛

1.安徽建筑大学机械与电气工程学院，合肥，2306012.安徽建筑大学建筑机械故障诊断与预警技术重点实验室，合肥，230601

0 引言

疲劳是材料退化的过程，是对其所承受循环载荷的响应[1]。在各类人造结构和自然系统中，疲劳是最主要的失效形式之一[2]。材料的疲劳寿命预测一直是工程界和学术界关注的热点问题[3]。从能量角度看，疲劳损伤是由内摩擦导致热耗散的不可逆过程，而热力学熵[4-5]是系统无序、系统紊乱的度量，能够描述材料的不可逆退化，可以作为材料疲劳损伤评估指标。

热力学熵相比于传统疲劳分析评估方法能够更好地解释疲劳损伤过程的物理机制。在利用热力学熵进行材料疲劳过程分析及寿命预测方面，BRYANT等[6]基于损伤力学与广义热力学理论，指出了熵产与材料损伤的不可逆性相关联，通过试验发现在改变试验条件的情况下，材料的最终断裂熵值仍为定值。AMIRI等[7]开发了一种基于熵流特征量评估临界疲劳损伤值的方法，确定了不同材料试样在经受弯曲疲劳作用时的熵流，并评估了临界损伤值。陈凌等[3,8-9]从熵守恒定律和能量守恒定律出发，推导出了一种新的低周疲劳寿命预测模型。NADERI等[10]通过疲劳断裂熵(fatigue fracture entropy，FFE)这一热力学熵特征量阐述了熵产和损伤变量之间的关联规律，并在此基础上提出了一种实时疲劳寿命检测单元。

上述研究表明，热力学熵相关特征量可进行疲劳寿命预测以及疲劳损伤评估，并且更加贴近疲劳损伤的机理层面，具有广阔的应用前景。目前国内在基于热力学熵的构件疲劳损伤评估方面研究较少，熵产率、累积熵产等热力学熵特征与疲劳损伤的关联特性尚未明确。本文选取Q235钢试样开展不同加载条件(加载幅值、加载频率)下的低周疲劳试验，利用熵产率、累积熵产、疲劳断裂熵等热力学熵特征量的变化特征描述低周疲劳损伤过程，并评估低周疲劳损伤程度，基于热力学熵相关特征量建立了一种新的寿命预测模型。

1 理论基础

疲劳是能量耗散的不可逆过程，由Clausius-Duhem不等式[11-14]可知，在产生内摩擦的固体材料中，所有变形都会导致正熵产值，表达式如下：

(1)

式(1)描述了熵产过程，它由塑性变形引起的塑性应变能耗散：

式中，f为试验频率；Δwp为塑性应变能。

(2)

因此式(1)可简化为

(3)

在以塑性应变为主的金属低周疲劳过程中，仅考虑式(3)第一项即可。其熵产表达式可表述为

(4)

即

(5)

其中，Δwp可根据Morrow[18]的理论，由以下循环塑性能耗公式确定[16,19-20]：

(6)

式中，σ′f为疲劳强度系数；ε′f为疲劳延性系数；b为疲劳强度指数；c为疲劳延性指数；Nf为疲劳失效循环周次。

对式(5)从起始时刻t=0到断裂时刻t=tf进行积分，可得到总熵增计算公式：

(7)

利用试验采集的试样标距内最大温度数据，通过式(5)和式(7)可以计算低周疲劳过程的热力学熵产率及累积熵产，为基于热力学熵的低周疲劳损伤评估以及疲劳寿命预测模型的建立提供了理论基础。

2 热像特征采集与数据分析

2.1 材料及试样

试验材料为Q235板材试样，尺寸如图1所示，经X射线荧光光谱分析，得到材料所含元素质量分数如表1所示。试样由激光切割加工，并沿轴向打磨抛光，为提高试样表面发射率，试验前将待测试样表面均匀喷涂一层黑漆。

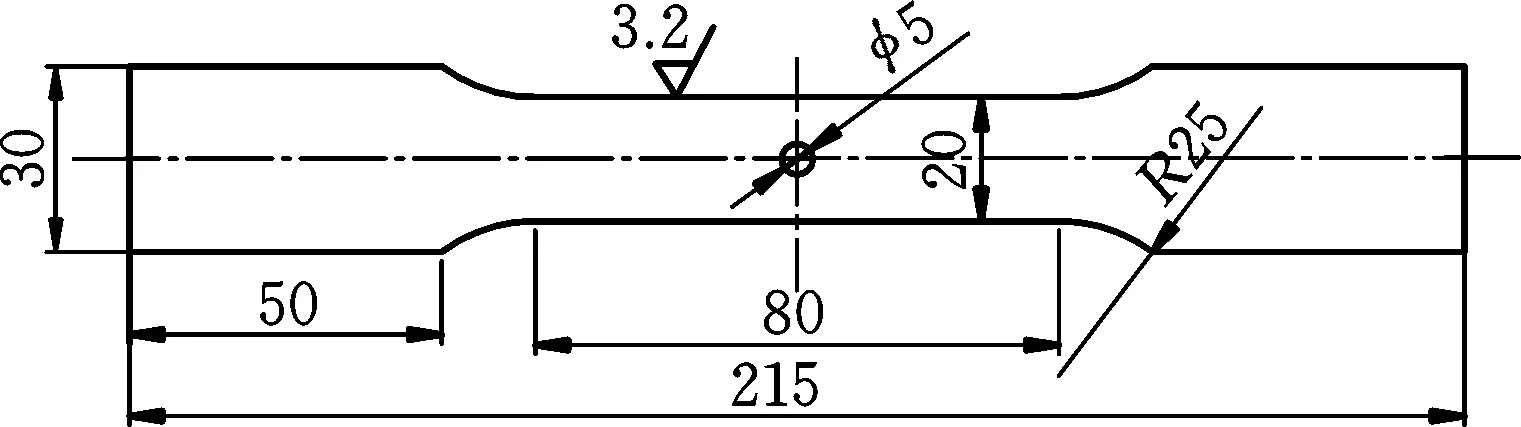
图1 Q235板试样(mm)Fig.1 Sample of Q235 plate (mm)

%

进行疲劳试验前，对Q235钢试样进行静态拉伸试验，试验结果表明，材料的抗拉强度为415 MPa，条件屈服极限为300 MPa。图2所示为Q235钢试样在拉伸载荷(以12.5 kN为例)作用下的应力、应变分布。由图2可见，试样所受的最大等效应力值为252.7 MPa，最大真实应变为0.129 3%，符合低周疲劳试验条件。

图2 Q235试样应力场与应变场云图Figure.2 Q235 samples stress and strain field cloud map

2.2 红外热像特征采集

图3所示为红外热像采集系统。本试验主要研究承受轴向循环载荷的Q235材料试样疲劳行为，使用电液伺服疲劳试验机(中机试验SDS-200)开展疲劳试验。为避免试验场所存在的自然光直射，试验全过程在室内进行。试验环境空气介质无强对流现象，相对稳定，环境温度为常温25 ℃。

图3 红外热像采集系统Fig.3 Infrared thermal image acquisition system

如图4所示，使用FLUKE Ti200红外热像仪对试验过程中试样表面温度进行实时监控，热像仪分辨率为640像素×480像素,热敏度不超过0.05 ℃。温度数据以红外热像图的形式保存。采集到的红外热像图使用SmartView软件分析处理，提取试样标距内最高温度值(相当于裂纹尖端温度)，采集该温度值作为疲劳过程温度演化数据。表2为Q235试样低周疲劳试验加载条件。

图4 Q235钢试样低周疲劳试验过程表面温度Fig.4 Surface temperatures of Q235 samples low-cycle fatigue test

序号加载频率f(Hz)加载幅值F(kN)最终循环次数(r)11011.06 68021012.02 93031012.51 14041013.05105812.583261012.51 14071512.51 30582012.51 584

2.3 红外热像特征数据分析

图5、图6所示分别为不同加载幅值和频率下的Q235试样低周疲劳过程温度演化曲线。图中可见低周疲劳试验全过程的温度演化分为3个阶段。第一阶段，试样表面温度从环境温度快速上升，这一阶段试样受到循环载荷影响，内部发生位错运动，表面产生侵入挤出现象，试样内部产能无法快速传递到外界，导致表面温度升高。第二阶段，试样表面温度相对平稳，试样内部产能与外界能量交换处于相对平衡状态。第三阶段，试样表面温度迅速上升，产生宏观裂纹及大塑性变形最终试样发生断裂。

图5 不同加载幅值下的温度演变曲线Fig.5 Temperature evolution curve under different loading amplitudes

由图5可知，循环载荷幅值越大，第一阶段试样初始温升速度越快，第二阶段的温度越高，并且试样最终的断裂温度越高。

由图6可知，对于不同加载频率，其频率越低，第一阶段温升斜率越大，且第二阶段的温度相对较高，试样断裂时其表面温度无显著差异。

图6 不同加载频率下的温度演变曲线Fig.6 Temperature evolution curves under different loading frequencies

3 热力学熵特征分析

3.1 不同加载条件下的熵产速率

图7、图8所示分别为不同加载幅值与频率下的Q235试样低周疲劳过程熵产率曲线。图中可见，在不同载荷幅值和加载频率下，熵产率值基本为定值，波动较小。在最初加载与最终断裂阶段，试样表面温度升高导致熵产率值发生小幅度下降。当试样内部产热功率和热耗散率基本稳定时，熵产率也相对稳定，该阶段占据试样的大部分疲劳寿命。

图7 不同加载幅值下的熵产率曲线Fig.7 Entropy generation rate curves under different loading amplitudes

图8 不同加载频率下的熵产率曲线Fig.8 Entropy generation rate curves under different loading frequencies

熵产率作为材料热力学维度的损伤速率，由图7可知，较小的加载幅值使试样在循环载荷作用下产生的能量释放较少，表面温升较低，因此，加载幅值较小时熵产率相对较低。加载幅值越高，单位时间产生的塑性应变能越多，熵产率越大。

如图8所示，载荷频率降低，材料损伤进程减缓，释放出较低的能量，表面温升较低，因此，加载频率越低熵产率越低。

3.2 低周疲劳过程累积熵的变化趋势

疲劳过程的累积熵产可用熵产率曲线与时间横轴围成的面积表示，即通过熵产率对时间进行积分获取。图9和图10所示分别为不同加载幅值和频率下的熵产累积变化曲线。图中可见，疲劳过程的热力学熵产累积是一个准线性累加过程。试样最终断裂时，累积熵产值达到最大即疲劳断裂熵。

图9 不同加载幅值下的熵累积曲线Fig.9 Entropy accumulation curves under different loading amplitudes

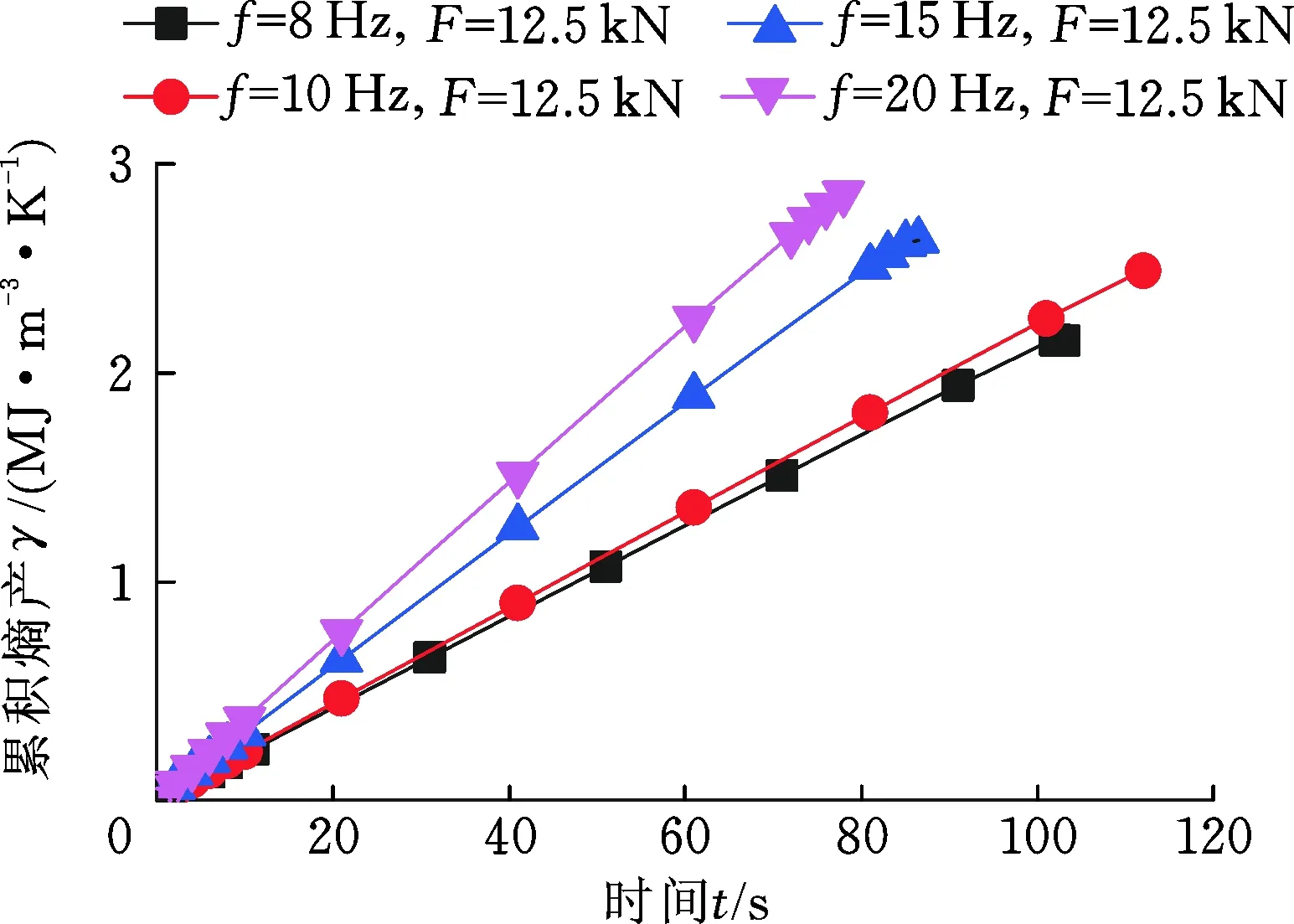
图10 不同加载频率下的熵累积曲线Fig.10 Entropy accumulation curves under different loading frequencies

由图9可知，加载载荷越大，累积熵产曲线斜率越大，越快达到累积熵产顶点，即在不同加载载荷下，加载幅值越大，试样断裂越快，熵产累积速率越快，熵产累积时间越短，其最终疲劳断裂熵值越小。

由图10可知，加载频率越高，熵累积速率越快，即累积熵产曲线越陡，越快达到断裂熵值。与此同时，同一加载幅值不同加载频率下，试样的疲劳断裂熵值相对一致，本试验中，在加载幅值为12.5 kN条件下，不同加载频率的疲劳断裂熵值约为2.579 MJ/(m3·K)。

3.3 低周疲劳的疲劳断裂熵

图11所示为Q235试样在相同频率不同载荷下的疲劳断裂熵值。由图可见，低周疲劳过程Q235钢试样的疲劳断裂熵随加载幅值的增大而减小。

图11 Q235试样低周疲劳试验同频率下的疲劳断裂熵Fig.11 FFE of Q235 low cycle fatigue testsunder the same frequency

图12所示为两组载荷相同、加载频率不同的疲劳断裂熵值散点图。由图可见，Q235钢试样的疲劳断裂熵与加载频率无明显关系，仅与加载载荷相关。本试验中，加载幅值为12.5 kN时和11.0 kN时，不同加载频率下的疲劳断裂熵值约为2.579 MJ/(m3·K)和5.656 7 MJ/(m3·K)。

图12 Q235试样低周疲劳试验同载荷下的疲劳断裂熵Fig.12 FFE of Q235 low cycle fatigue tests under the same load

3.4 基于热力学熵的疲劳寿命预测模型

在分析疲劳断裂熵与加载幅值的关系的基础上，利用指数函数建立载荷与断裂熵之间的函数模型：

γf=AeBF

(8)

其中，A、B为模型参数。表3为函数模型回归试验数据及拟合参数。

表3 拟合模型参数表

图13所示为载荷幅值与疲劳断裂熵之间的拟合曲线。图14为利用试验数据对模型进行验证的误差分析图，模型验证误差小于18%。

图13 载荷幅值与疲劳断裂熵拟合曲线Fig.13 Fitting curve of load amplitude and fatigue fracture entropy

图14 模型验证误差分析曲线Fig.14 Error analysis of model verification

前述研究表明，低周疲劳过程疲劳断裂熵可根据相应的加载幅值求得。在疲劳损伤过程中，提取材料表面温度信息后就可以计算实时熵值，将其与疲劳断裂熵对比可进一步评估材料损伤状态。将累积熵产与循环周次归一化，归一化后累积熵产与循环周次近似为线性关系，如图15及下式所示：

图15 归一化熵产与归一化循环周次Fig.15 Normalized entropy production and normalized cycle times

(9)

对式(9)进行变形得到：

(10)

将式(8)代入式(10):

(11)

由式(9)和式(11)可见，疲劳损伤过程某一熵产累积值对应于一特定损伤状态。作为衡量系统不可逆性和组织无序性的特征参数，熵产可用来描述材料内部位错、滑移等导致的不可逆损伤。

另外选取6组同批次Q235钢试样开展低周疲劳试验，加载幅值均为11.5 kN，加载频率均为10 Hz，其中，1～4组分别提取试样在不同循环周次下的表面温度信息，从而获取该状态的热力学熵特征，对寿命进行预测，用于模型验证。5、6两组采集试验过程中的应力幅值和应变幅值数据，运用经典Manson-Coffin和Basquin模型[9]开展寿命预测对比，结果见表4。

表4 疲劳寿命预测模型验证结果

表4数据表明，传统的Manson-Coffin和Basquin模型与本文的寿命预测模型预测误差均在14%～30%范围内，本文模型可用于疲劳寿命预测。本文模型可通过提取试样疲劳过程的各阶段特征进行寿命预测，与传统模型相比更具实时性。

4 结论

(1)本文选取熵产率和累积熵产作为疲劳损伤评估指标，通过研究发现，同一加载幅值下疲劳损伤过程熵产率基本恒定，且熵产率随着加载幅值及频率的增大而增大。疲劳损伤过程热力学熵的累积是一个准线性累加过程，其熵产累积速率随着加载幅值和频率的增大而加快，即熵产曲线的斜率越大，越快达到熵产曲线顶点。

(2)选取Q235材料试样开展不同加载幅值和加载频率下的低周疲劳试验。试验发现，不同加载条件下疲劳断裂熵随加载幅值增大而减小，与加载频率无明显关系。

(3)明确了疲劳断裂熵与加载幅值之间的函数关系，并通过分析归一化的疲劳累积熵与循环周次关联特性，建立了疲劳寿命预测模型，为金属构件疲劳寿命预测提供了新思路。

(4)后续将开展热力学熵特征量、磁特征量等多特征量融合的疲劳损伤评估，以降低评估不确定性，提高评估精度。这也是开展疲劳损伤研究的重点和难点。