地震及多风况下风力机塔架动力响应
2019-09-03邹锦华王渊博刘中胜
邹锦华 杨 阳 李 春,2 王渊博 刘中胜
1.上海理工大学能源与动力工程学院,上海,200093 2.上海市动力工程多相流动与传热重点实验室,上海,200093
0 引言
近年来,风能因其资源分布广泛及清洁无污染等特点成为能源转型的重要方向[1]。2016年,我国风力发电新增装机容量为23.4 GW,总装机容量超过168.7 GW,占全球总装机容量的35%[2-3]。我国“十三五”期间将确保并网装机容量达到210 GW,以实现风电占总发电量6%的目标[4]。我国风资源丰富的东南沿海和西北地区分别处于环太平洋地震带和亚欧大陆地震带,风力机在地震激励下易出现材料变形或失效,塔架结构安全受到极大威胁。此外,受蒙古高压的影响,我国风速在季节上呈现“冬春大,夏秋小”的特点[4-7],且东南沿海夏秋季台风现象多发,最大平均风速达28.2 m/s。塔架结构响应在复杂多变的风况及地震作用下更加剧烈复杂,易发生塔架结构振动失稳甚至倾覆毁坏,因此,开展湍流风与地震联合作用下塔架动力响应研究具有重要意义。
在该领域,国内外学者开展了一些相关研究。文献[8]改进传统的频率分析法,结合风力机受载特性修正地震作用的叠加方法,计算了2 MW风力机在18 m/s湍流风与地震联合作用下的动力响应,并与风力机设计软件GH Bladed的结果进行对比,验证了振型分解法的有效性。文献[9]采用有限元法建立了风力机塔架、基础与地基间的相互作用模型,以刚度较大的圆盘模拟风轮,计算了13 m/s定常风与地震条件下不同地基中的风力机的动力响应,结果表明地基会改变风力机的自振频率,并在一定程度上增大塔架剪力和弯矩响应。文献[10]通过ANSYS分析了地震载荷多个输入角度时不同地面加速度峰值(peak ground acceleration,PGA)下风力机的塔架位移响应,对风载荷进行面积分以计算推力,结果显示地震波方向与塔架开口方向一致会导致塔架动力响应峰值较大。文献[11]建立了1.65 MW风力机有限元模型,考虑不同阻尼比和垂直方向振动的影响,计算了风力机破坏概率,发现随风力机塔架高度的增大,塔架结构在地震作用下更易屈服。文献[12]运用土木工程分析软件SAP2000建立5 MW风力机模型,将风载荷转化为定常风轮推力,研究了不同土质的地震垂直分量对风力机结构动力响应的影响,发现地震激励会导致风力机塔架出现屈服破坏。上述研究侧重于地震对风力机塔架结构的影响,目前尚缺乏对不同强度风载荷与地震联合作用下风力机动力学响应的研究。
文献[13]采用大型振动台测试小型风力机地震作用下的动态响应,验证了运行中的风力机受气动阻尼影响时塔架振动幅度与停机状态相比差异较大。文献[14]基于开源风力机仿真软件FAST建立了湍流风场与地震实时耦合模型,模拟了18 m/s风况下风力机动力学响应,发现湍流风及地震载荷均大幅加剧了机舱加速度变化,并使塔基载荷增大到稳态风工况的2~15倍。
为研究风力机塔架结构在多种风况与地震联合作用下的动力学响应,本文以美国可再生能源实验室(National Renewable Energy Laboratory, NREL) 5 MW风力机为研究对象,基于Wolf方法考虑土体与风力机基础之间的相互作用,采用多体系统动力学方法建立了风力机模型。利用开源风力机仿真软件FAST计算了湍流风与地震联合作用下塔架动力学响应,为风力机塔架设计与安全评估提供参考。
1 研究对象及仿真模型
FAST(Fatigue, Aerodynamics, Structures and Turbulence)是NREL开发的一款分析风力机气弹特性的开源软件[15]。它采用Kane方法和模态截断法建立风力机塔架和叶片等柔性结构模型,具有较高的求解效率,其计算精度获得德国劳氏船级社(Germanischer Lloyd,GL)认证,具有较高的可靠性。
1.1 研究对象
以NREL 5 MW风力机为研究对象[16],其主要结构和性能参数如表1所示。
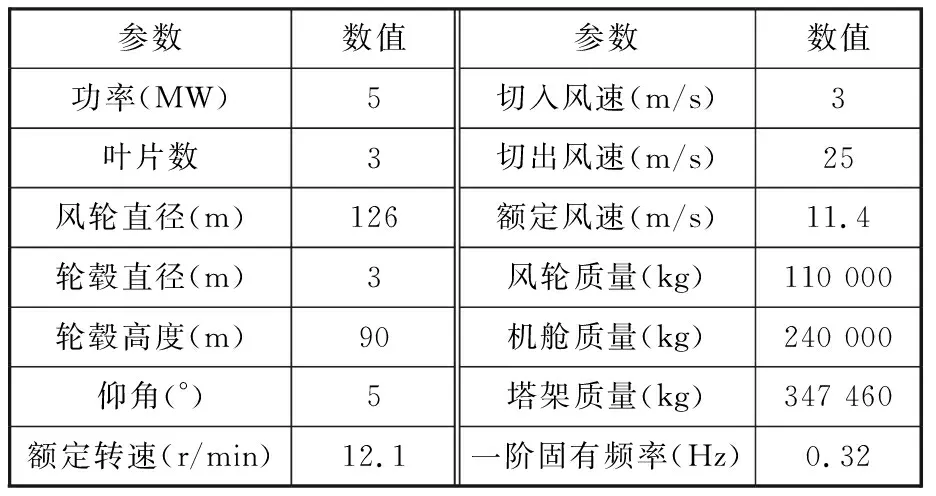
表1 NREL 5 MW风力机主要参数
1.2 土-构耦合模型
风力机结构与地基是相互耦联的复杂体系,结构体与土体之间弹性模量等物性的差异导致两者之间存在力的相互作用和形变的互相约束[17]。对处于地震多发地区的风力机,考虑土-构耦合作用是动力分析的必要前提。根据Wolf理论,可在土体与结构体之间设置弹簧和阻尼器的方法模拟土与结构之间的应力与应变[17-18]。图1为风力机基础平台与土体耦合模型示意图,对于刚性圆柱型基础,刚度K及阻尼系数C分别为
(1)
(2)
式中,i(i=x,y,z)为方向;ρs为土体密度;ci为特征波速;r0为基础的特征半径;A0为基础特征面积;z0为基础高度;cs为剪切波速;λ为结构系数,当i=x,y时,λ=0.575,当i=z时,λ=0.85;Gs为土体剪切模量。
在水平和竖直方向上,特征波速为
(3)
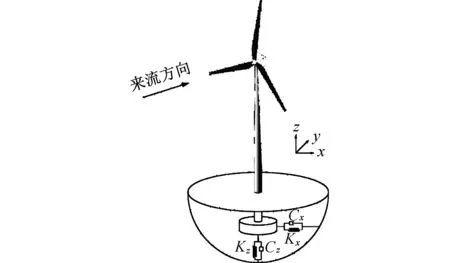
图1 风力机基础平台与土地耦合模型Fig.1 Interaction model for wind turbine platform and soil
将式(3)代入式(1)、式(2)可得
(4)
(5)
土体发生形变时,基础部分的高径比为
(6)
式中,υ为土体的泊松比。
将式(6)代入式(4)、式(5)即可得到弹簧振子的刚度K及阻尼系数C:
(7)
(8)
2 湍流风场与地震运动
为研究风力机结构响应与风速及地震强度之间的关系,计算30种强度的地震激励及5种风速的风载荷共同作用下的风力机动力响应,共150个算例。仿真时间为600 s,时间步长为0.005 s,地震载荷在400 s时加入,持续时间为50 s。
2.1 湍流风场及气动载荷计算
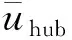
(9)
式中,f为频率;Lζ为积分缩放因子;σs为ζ方向上的标准差。
根据IEC标准,Lζ定义如下:
(10)
式中,湍流因子Λu为42;标准差σy和σz分别为0.8σx和0.5σx。

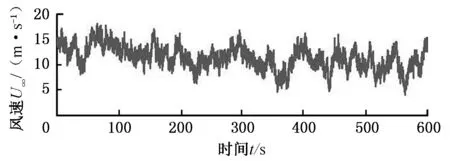
图2 风力机轮毂高度处风速Fig.2 Wind speed at hub height of the wind turbine
根据叶素动量理论,叶片由若干叶素连接组成,因此将风力机叶片划分为多个微元段,微元高度为dr,假设各微元段的受力相互独立,从而根据翼型特性计算气动力。
图3为叶片微元段的速度三角形及气动力示意图,其中α、β和φ分别为翼型的攻角、桨距角和入流角;W、U∞、ω分别为气流相对速度、来流风速和风轮转速;α′为切向诱导因子。
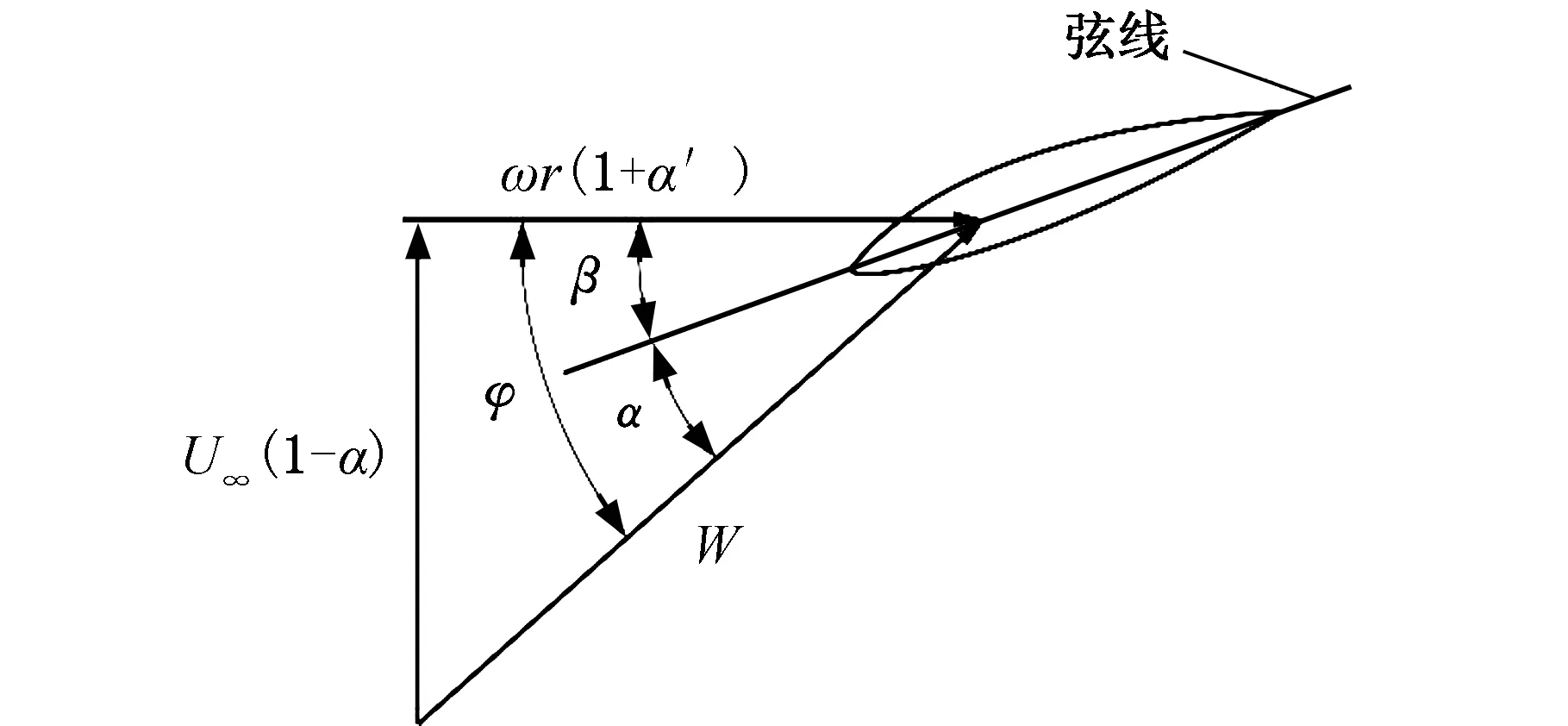
(a)翼型速度三角形

(b)气动力图3 翼型速度三角形及气动力Fig.3 Wind speed velocity triangle and aerodynamic force
根据速度三角形,可计算得相对速度W为
(11)
根据翼型气动特性,叶素的气动升力δFL和气动阻力δFD分别为
(12)
(13)
式中,CL与CD分别为升力系数和阻力系数;ρa为气流密度;c为翼型弦长。
将叶素上的气动升力δFL和气动阻力δFD沿轴向和切向进行分解,可计算得叶素的轴向气动力δFx和切向气动力δFy:
δFx=δFLcosφ+δFDsinφ
(14)
δFy=δFLsinφ-δFDcosφ
(15)
对轴向气动力δFx和切向气动力δFy沿翼展方向进行积分即可得到整个叶片的气动力,同时引入动态入流理论和Prandtl理论修正叶尖损失以精确计算风轮气动力[21]。
2.2 地震加速度谱及地震载荷计算
通过匹配目标谱方法获得30组地震加速度时域历程以表征不同强度的地震运动。
对加速度时间序列采用小波函数拟合地震设计谱[22]。针对任意初始加速度时间序列a(t)和目标谱,可通过图4所示的方法进行匹配。图5所示是谱加速度(PSA)为0.60g时,x方向加速度时域变化及目标谱匹配情况。tj时刻初始谱与目标谱之间的误差:
ΔRj=(Qj-Rj)
(16)
式中,Qj为目标谱值;Rj为初始谱值。
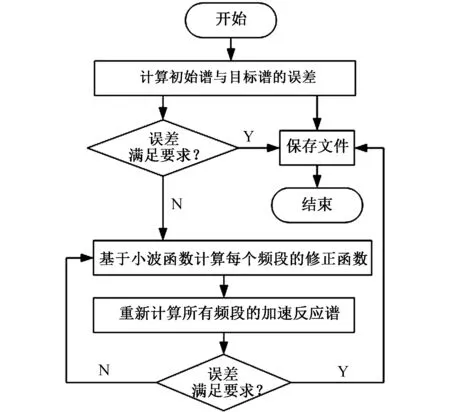
图4 目标谱匹配过程流程图Fig.4 Flowchart of response spectrum match
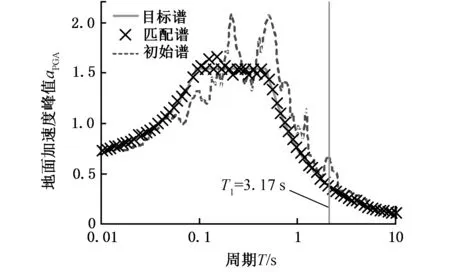
图5 地震x方向加速度目标反应谱匹配情况Fig.5 The acceleration of earthquake target spectrum and matched spectrum in x direction
假设反应谱的峰值时间t不受修正函数影响,则调整时间序列如下所示:
(17)
fi(t)=hi(ti-t)
(18)
(19)
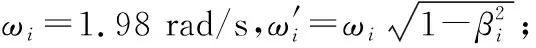
加速度反应谱δRj为

(20)
将式(17)代入式(20)可得
(21)
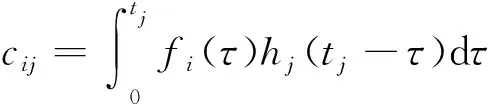
b=C-1δR
(22)
计算式(22)可得修正函数幅值b,以此计算调整时间序列δa(t)。第一次匹配后,加速度时间序列a1(t)为
a1(t)=a(t)+γδa(t)
(23)
式中,a(t)为修正前加速度;γ为修正函数的松弛因子,γ∈(0,1)。
在第二次匹配中,a1(t)替代a(t)为新的加速度时间序列,如此反复直至目标谱匹配达到目标精度。
地震发生时,基础平台的目标加速度为地震加速度,此时基础平台ζ方向地震载荷Fζ为
(24)
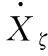
3 结果分析
3.1 有效性验证
为验证计算模型的有效性,计算了额定风速下风力机受到加速度峰值为0.3g地震激励时塔顶位移响应,并将结果与GH Bladed软件的计算结果进行对比。塔顶水平方向位移动态响应如图6所示。可以看出,对于塔顶横向位移响应,FAST计算结果在地震作用后期波动逐渐减小,而GH Bladed计算结果保持一定的波动,但两者误差较小。对于塔顶侧向位移,FAST计算结果与GH Bladed结果变化与幅值基本相同。这说明所采用的计算工具与研究方法具有合理性和有效性。
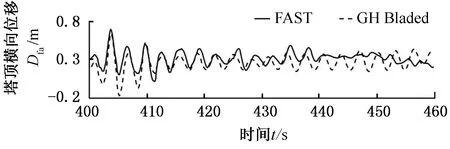
(a)塔顶横向位移
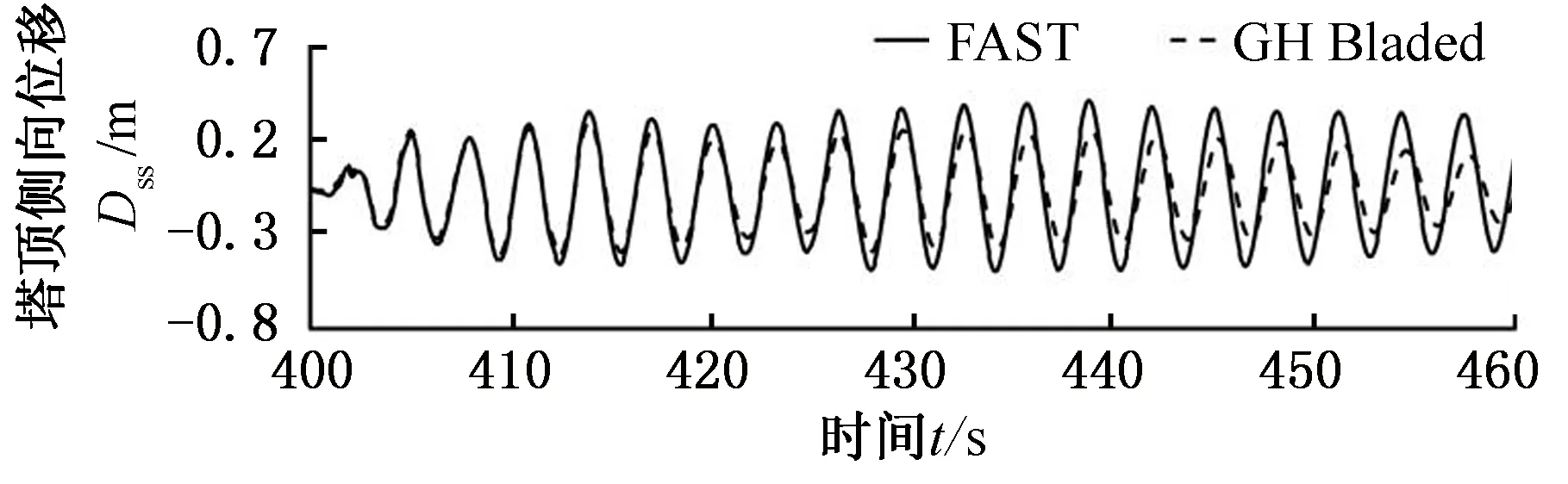
(b)塔顶侧向位移图6 地震工况塔顶水平方向位移动态响应对比Fig.6 Comparison of the dynamic response for tower top displacement on seismic condition
3.2 塔顶时域响应
图7所示为加速度峰值为0.30g时,不同风速下风力机塔顶位移动态响应。可以看出,随风
速增大,风力机塔顶位移波动幅度先增大再减小。在7 m/s风速下,地震激励引起的位移显著大于湍流风单独作用引起的位移。额定风速下,塔顶位移普遍大于其他风速下的动态响应,且湍流风影响与地震激励影响相当。随风速的增大,叶片受变桨控制和气动阻尼影响,风轮受到的非定常气动力降低,塔顶位移也随之降低,位移峰值均小于额定风速与地震联合作用时的峰值。同时,随着湍流风强度的增大,塔顶位移响应变化逐渐剧烈。
图8所示是加速度峰值为0.30g时,不同风速下塔顶加速度动态响应。可以看出,在低风速下,塔顶加速度受地震激励影响明显。地震发生后,7m/s风速下塔顶加速度均大于其他风速,说明在高风速下塔架振动能量可通过风轮转动所引起的气动阻尼耗散,因而低风速下塔顶加速度受地震影响明显。在无地震激励时,随风速增大,塔顶加速度也持续增大,说明高速湍流风对塔顶加速度影响较大,高强度湍流风变化剧烈,使风轮受到的气动载荷处于不稳定状态,从而使塔架振动加剧。
3.3 塔顶频域响应
图9所示为加速度峰值为0.30g时,不同风速下塔顶位移频域响应。
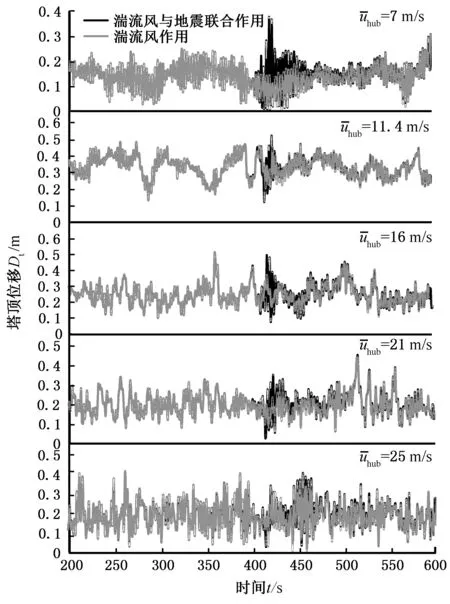
图7 不同工况塔顶位移动态响应对比Fig.7 Comparison for dynamic responses of tower top displacement on different conditions
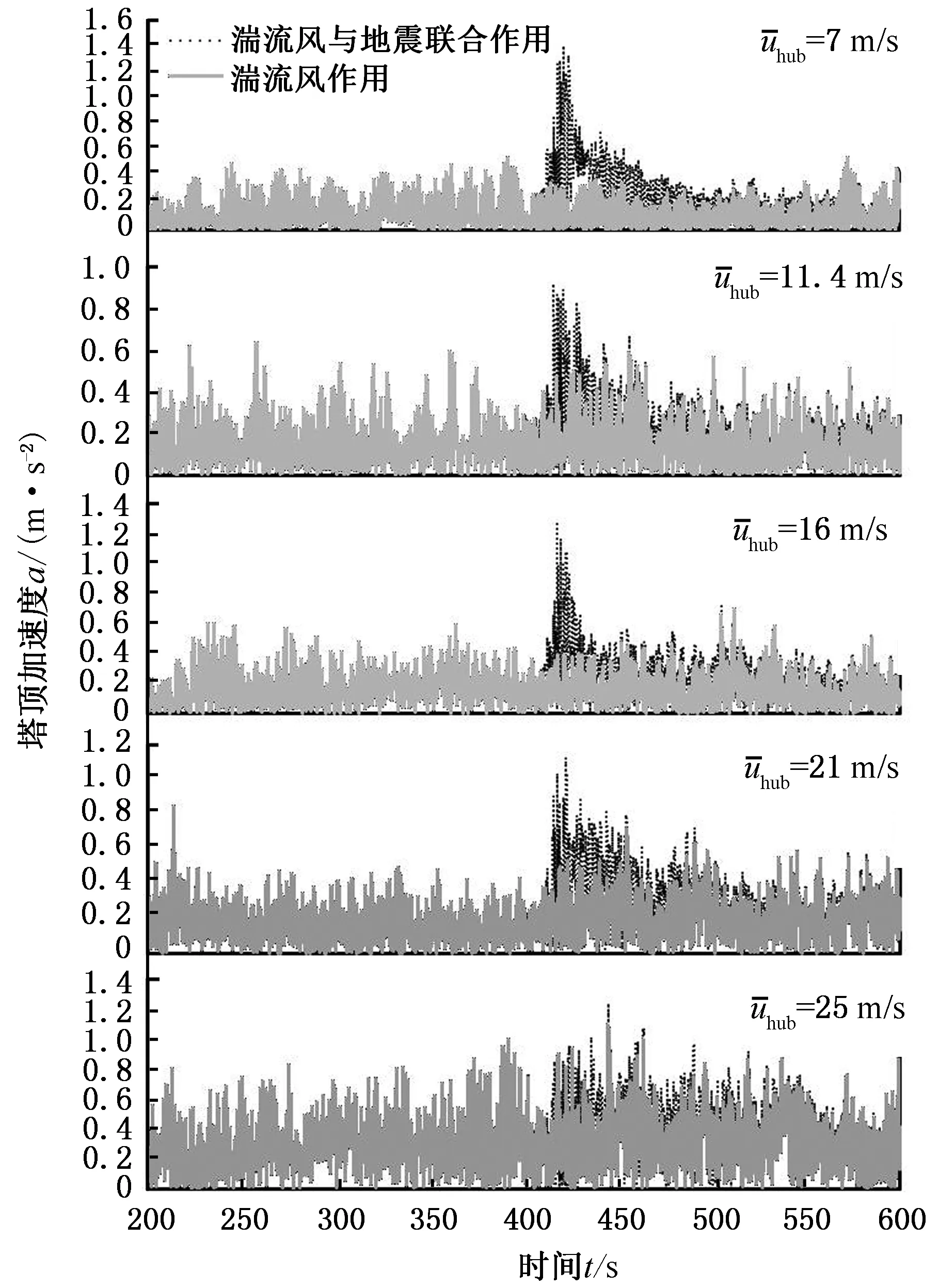
图8 不同工况塔顶加速度动态响应对比Fig.8 Comparison for dynamic responses of tower top acceleration on different conditions
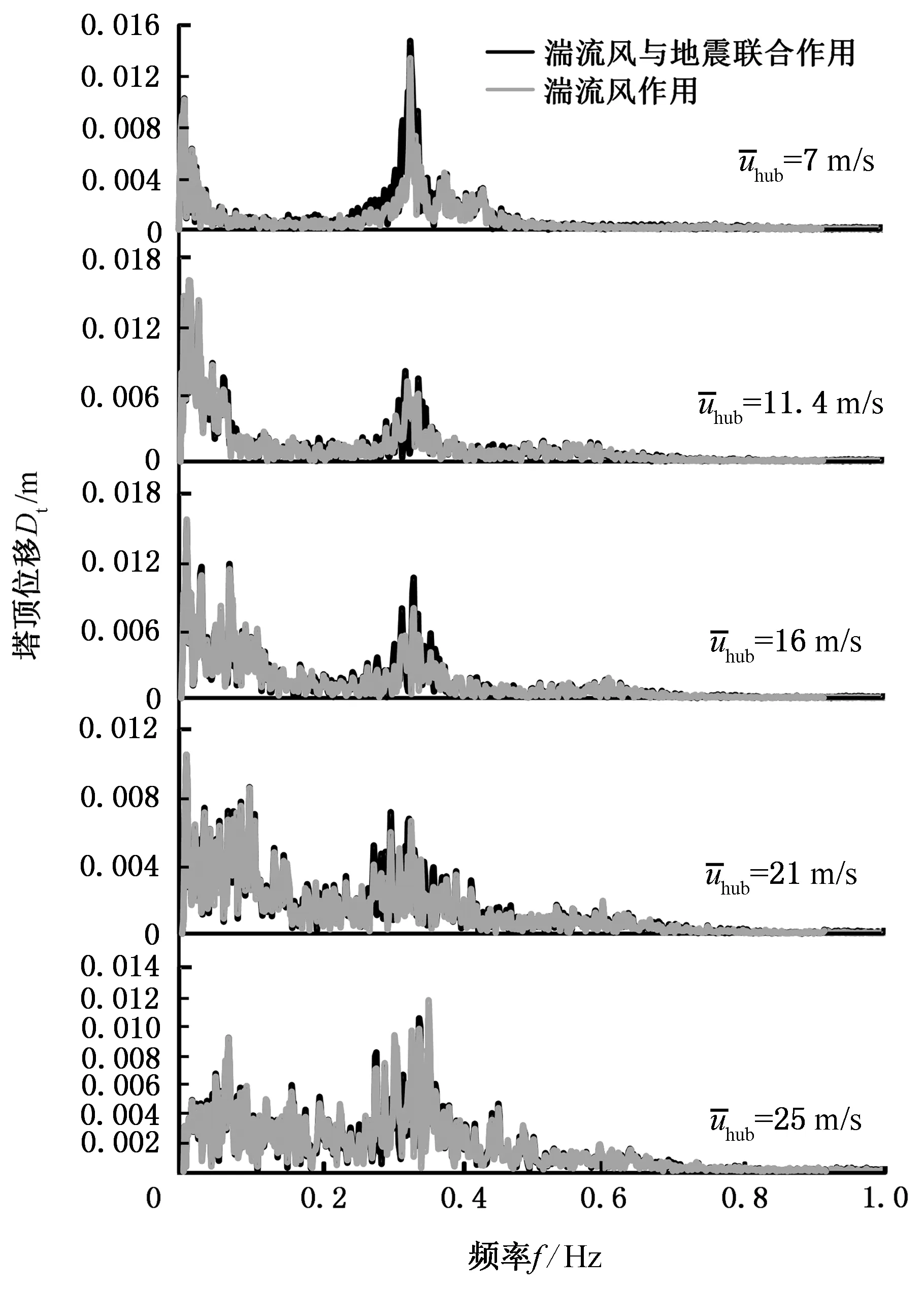
(a)横向
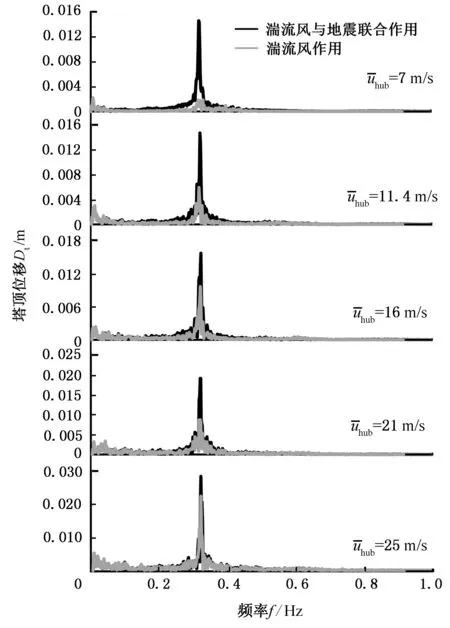
(b)侧向图9 不同工况塔顶位移频域响应对比Fig.9 Comparison for dynamic responses of tower top dis-pla cement on different conditions in frequency domain
图9a表明塔顶横向位移在0.001~0.18 Hz处有明显振荡,且随着风速的增大,此段频率处位移响应波动逐渐增大,这主要是因为湍流风能量集中在0.01 Hz附近,而横向为迎风面,因此受湍流风影响较大。同时,塔顶横向位移在塔架一阶固有频率0.32 Hz处出现较大的峰值,随着风速的增大,0.32 Hz处塔架横向位移先减小再增大。在湍流风与地震联合作用时,0.05~0.4 Hz处塔架横向位移响应有一定程度的增幅。图9b显示0.32 Hz处塔顶侧向位移出现明显的峰值,在湍流风单独作用时,0.32 Hz处塔顶侧向位移响应随风速的增大而增大,在湍流风与地震联合作用时,风速小于16 m/s时塔顶侧向位移变化较小,随着风速的增大,湍流风与地震耦合作用增大,塔顶侧向位移响应出现较大的增幅。
3.4 塔架动力响应
图10所示是加速度峰值为0.30g时,不同风速下塔架不同高度处的位移响应峰值。可以看出,7 m/s风速下塔架位移峰值最小,额定风速11.4 m/s时塔架位移峰值最大,且与16 m/s风速下响应程度相当。在额定风速之后,随着风速增大,塔架位移响应峰值逐渐减小。塔架高度小于20 m时,不同风速下位移响应峰值相差不大,塔架高于20 m时,随塔架高度上升,不同风速下位移峰值差距逐渐增大。
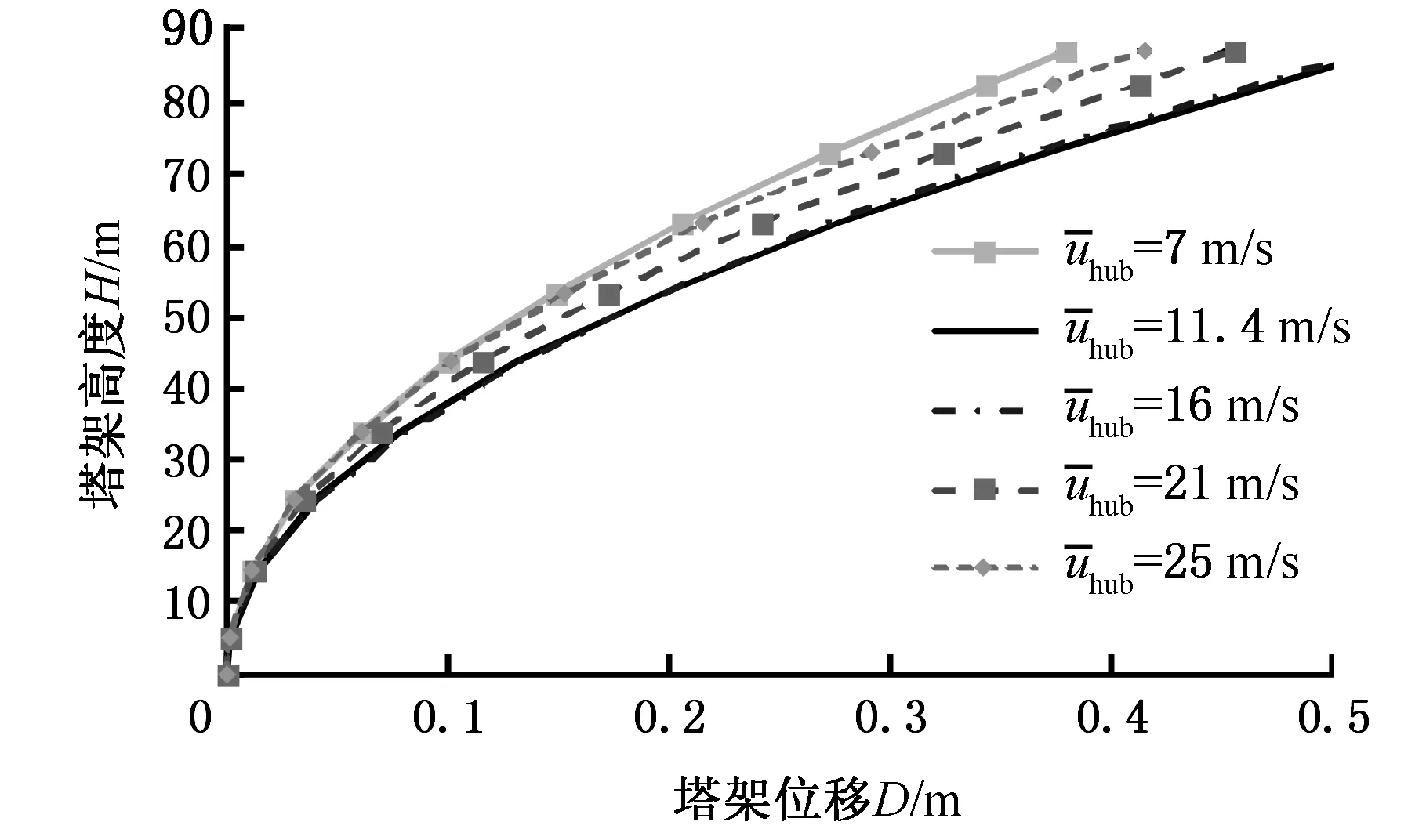
图10 不同风速下塔架不同高度处的位移峰值Fig.10 Tower displacement at different heights under different wind speeds
图11所示是加速度峰值为0.30g时,不同风速下塔架不同高度处的加速度响应峰值。可以看出,7 m/s风速下不同塔架高度处加速度响应峰值均大于其他风速下响应峰值;其他风速下加速度响应峰值均接近,说明地震激励作用对塔架加速度影响明显。在风速较大时,加速度响应受气动阻尼影响较大,因而塔架加速度响应峰值较小,同时,随着塔架高度上升,加速度响应峰值先增大而后急剧减小,最大值出现在塔架53.5 m处。
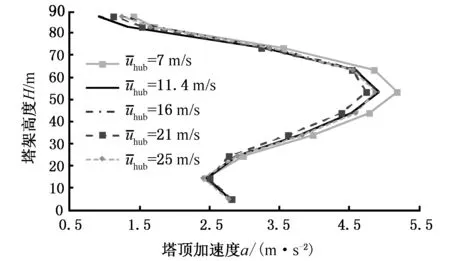
图11 不同风速下塔架不同高度处的加速度响应峰值Fig.11 Tower acceleration at different heights under different wind speeds
图12所示是加速度峰值为0.30g时,不同风速下塔架不同高度处的剪切力响应峰值。可以看出,风速小于11.4 m/s时,塔架高度大于30 m部分剪切力峰值变化较小,而风速大于11.4 m/s后,剪切力峰值出现较大的波动,在50~65 m处出现较深的凹部。随风速增大,塔架整体剪切力峰值先增大再减小,这主要是因为风速低于额定风速时,风速逐渐增大会导致风轮转速提高从而导致风轮推力增大,而在高风速下风力机采用变桨系统以控制输出功率和保证风力机安全,风轮推力变小,因而塔架剪切力响应峰值变小。
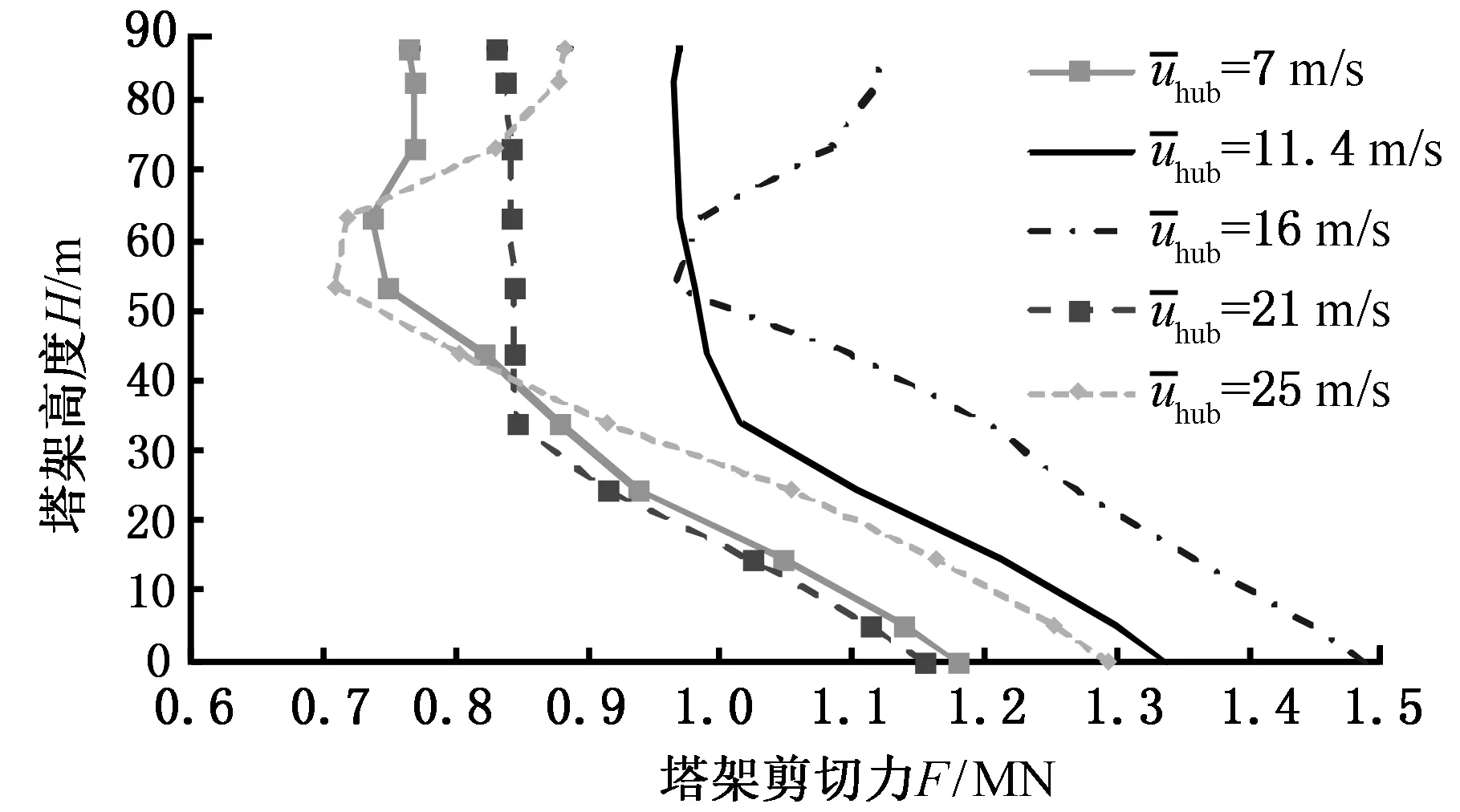
图12 不同风速下塔架不同高度处的剪切力峰值Fig.12 Tower shear force at different heights under different wind speeds
图13所示是加速度峰值为0.30g时,不同风速下塔架不同高度处的弯矩响应峰值。可以看出,在塔顶部位,弯矩随风速的增大而增大,在53~73 m高度处,16 m/s风速下塔架弯矩峰值最大,7m/s风速下弯矩峰值最小,而11.4 m/s、21 m/s及25 m/s风速下塔架弯矩峰值差距较小,在低于53m处,塔架弯矩峰值随风速的增大先增大再减小。这说明湍流风对塔顶弯矩影响较大,同时较大风速的湍流风作用会加剧塔架弯矩载荷。
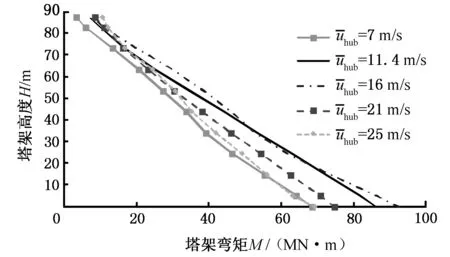
图13 不同风速下塔架不同高度处的剪切力峰值Fig.13 Tower bending moment at different heights under different wind speeds
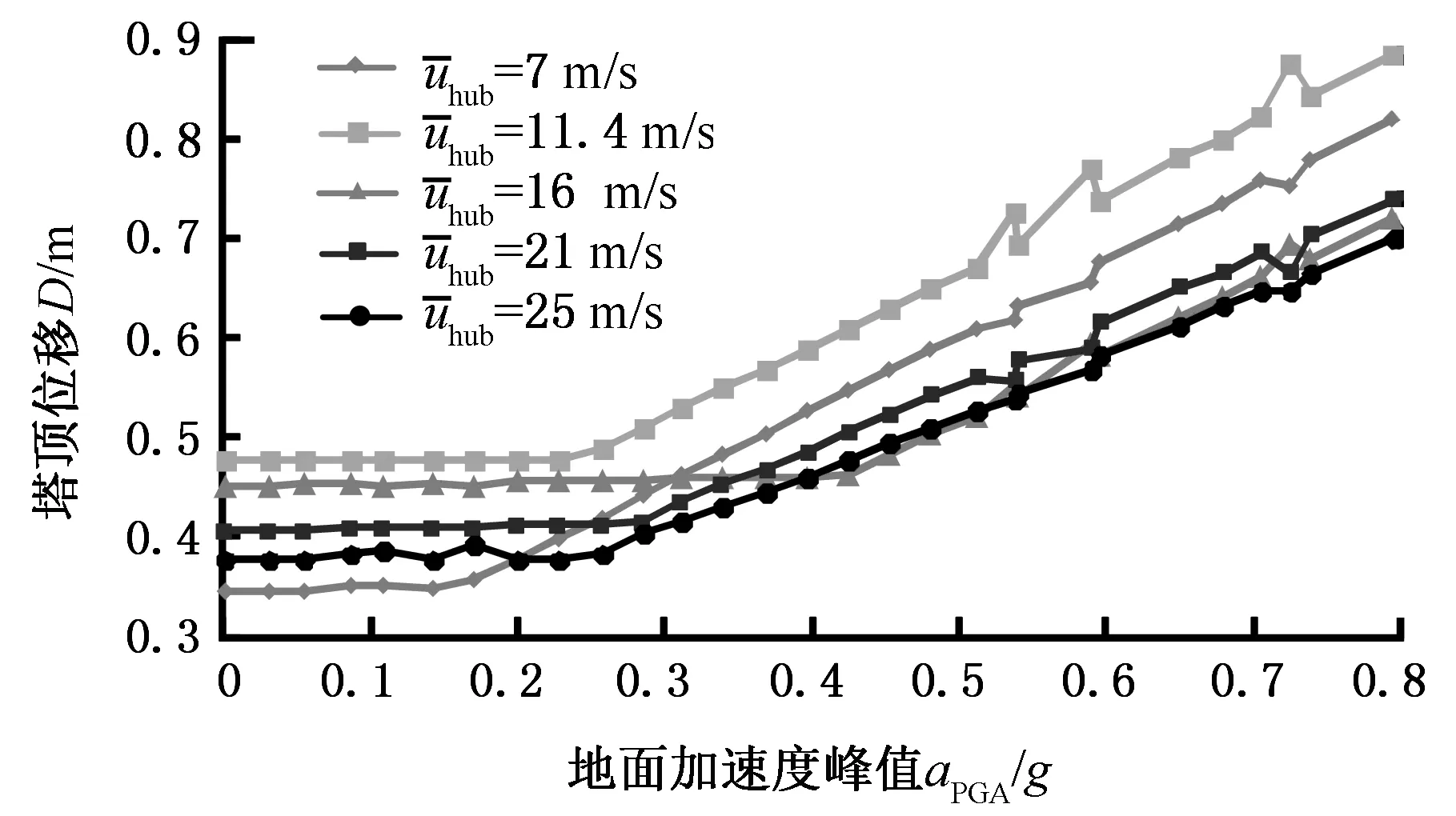
图14 不同风速下塔顶位移峰值Fig.14 Tower top displacement peak at different conditions
3.5 响应峰值分析
图14所示为不同风速下塔顶位移响应峰值。可以看出,不同地震强度下塔顶位移峰值均在额定风速11.4 m/s处。在不同风速的湍流风场中,随地震强度的增大,塔顶位移峰值均先保持不变,在大于临界点后,塔顶位移峰值随PGA增大近乎线性增长。在7 m/s风速下,PGA小于0.17g时,由于湍流风强度较低,塔顶位移小于高速风况时的塔顶响应,当PGA大于0.17g后,塔顶位移主要受地震载荷影响,在PGA大于0.30g后,塔顶位移峰值大于16 m/s、21 m/s和25 m/s风速下的响应峰值,这主要是因为高速湍流风强化了气动阻尼效果,使得地震引起的塔架振动能量可以较快耗散。7 m/s、11.4 m/s、16 m/s、21 m/s和25 m/s风速下塔架位移对应的临界PGA分别为0.17g、0.23g、0.41g、0.30g及0.28g,结果显示临界PGA随风速的增大先增大后减小,在低风速下,风轮受到的湍流风推力较小,因此塔架受到的风载荷偏小,而风速达到额定值后,风轮转速达到最大值,因而风轮推力较大,此时塔顶位移受风载荷影响较大,当风速接近切出风速时,风力机通过变桨系统控制叶片角度以达到额定功率输出,因而风力机叶片升阻比较大,从而实现在额定转速时升力较大而阻力较小,因此风轮所受推力较小,塔顶位移在高风速下受风载荷影响较额定风速时小。
图15所示为不同风速下塔顶加速度峰值。可以看出,在风速较低时,由于湍流风强度较小,塔顶加速度变化不大,因此7 m/s与11.4 m/s风速下塔顶加速度相近且偏小,同时,这两种风况下塔顶加速度临界PGA基本一致。在高风速下,塔顶加速度随风速的增大而增大,且对应的临界PGA也随之增大,说明在高风速风况下,风力机塔顶加速度受风载荷影响较大。在临界PGA之后,不同风速下塔顶加速度差距不大,表明在高强度地震作用时塔架加速度主要受地震载荷影响,受湍流风影响较小。

图15 不同风速下塔顶加速度峰值Fig.15 Tower top acceleration peak under different wind speeds
图16所示为不同风速下塔顶和塔基剪切力响应峰值。可以看出,在弱强度地震作用时,不同风速下塔顶与塔基剪切力相差不大。在塔顶部位,高风速下剪切力响应临界PGA随风速的增大而减小,表明风力机变桨控制可有效降低风轮推力。在额定风速11.4 m/s下,塔顶剪切力峰值曲线在PGA大于0.10g后出现缓慢上升的现象,说明额定风速的湍流风与地震联合作用会加剧塔顶剪切力响应。而在塔基部位,地震作用对剪切力响应影响明显,不同风速下的塔基剪切力峰值曲线均在PGA为0.10g处发生转折,且斜率基本一致。除额定风速外,不同风速下塔顶与塔基剪切力相近,这主要是因为高强度地震作用下地震载荷是塔架剪切力的主要载荷。

(a)塔顶
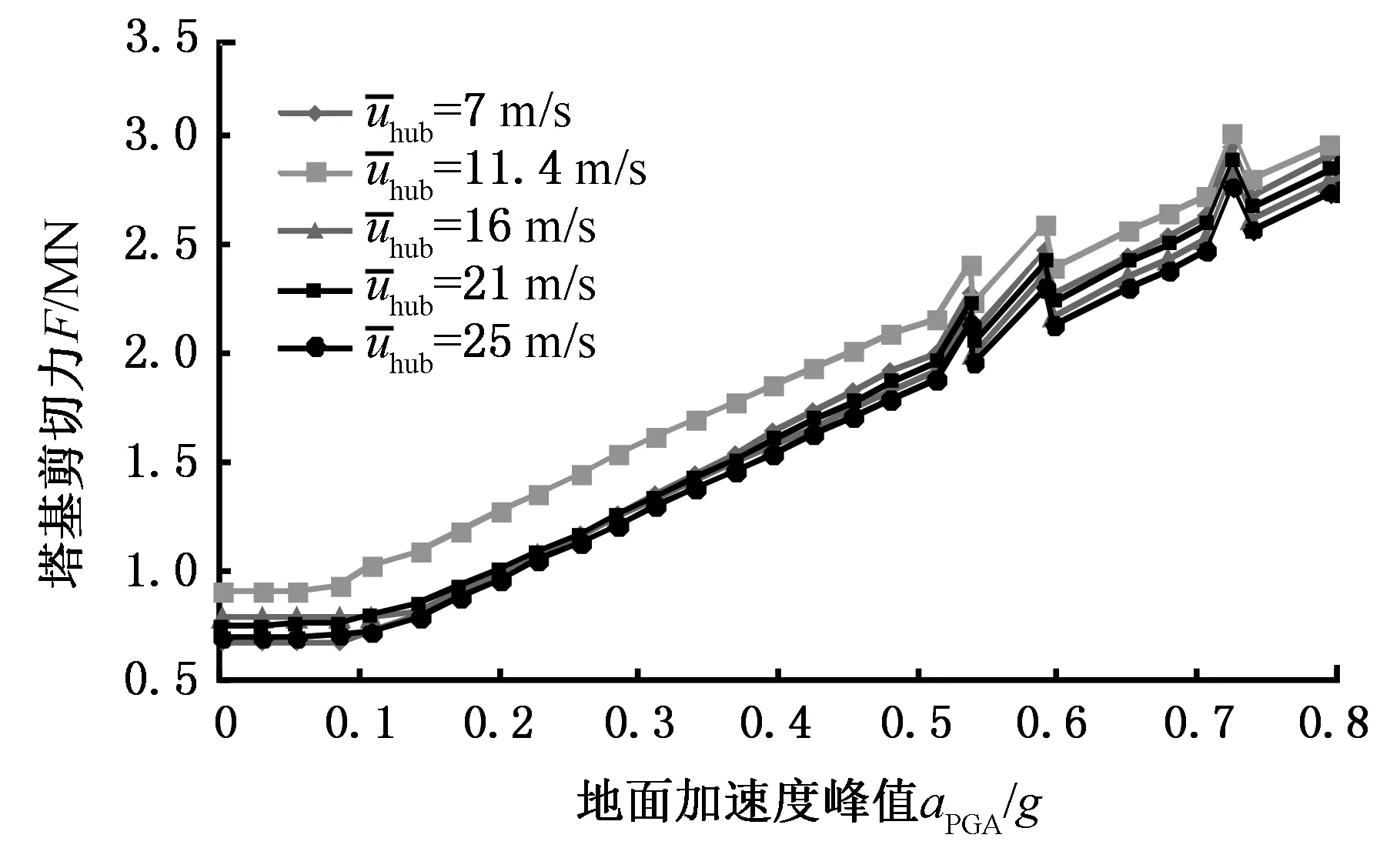
(b)塔基图16 不同风速下塔顶与塔基剪切力峰值Fig.16 Tower top and base shear force under different wind speeds
图17所示为不同风速下塔顶与塔基弯矩响应峰值。可以看出,塔顶弯矩受地震影响较小,仅有7 m/s及21 m/s风速时在高强度地震下塔顶弯矩有轻微增大,其余风速下塔顶弯矩变化很小。同时,塔顶弯矩随风速增大而增大,这主要是由于风轮在风速较高时升力增大,导致绕x轴力矩变大,因此在高强度湍流风下塔顶弯矩较大,又因风轮这一大质量部件存在,塔顶弯矩受地震载荷影响较小。对于塔基部位,由于额定风速下风轮推力较大,塔基弯矩略大于其他风速下的值,同时塔基弯矩的临界PGA随风速的增大而先增大再减小。

(a)塔顶
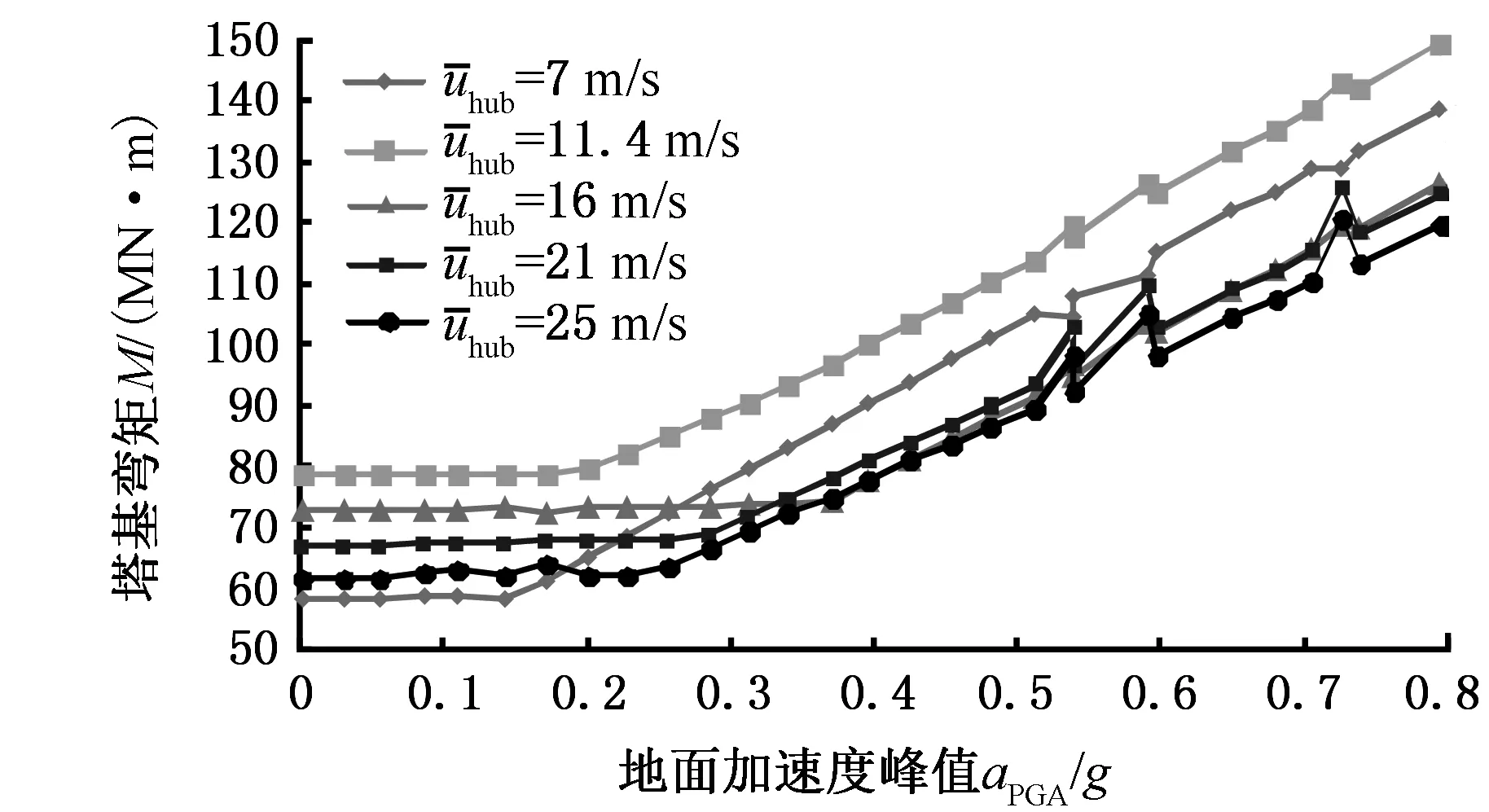
(b)塔基图17 不同风速下塔顶与塔基弯矩峰值Fig.17 Tower top and base bending moment under different wind speeds
4 结论
(1)基于风力机开源软件FAST及开发的第三方地震模块,根据Wolf理论和匹配目标谱方法,建立NREL风力机仿真模型,计算了7 m/s、11.4 m/s、16 m/s、21 m/s及25 m/s的湍流风与地震联合作用下风力机塔架结构动力学响应。
(2)低风速下,地震激励作用对塔顶位移响应影响明显;额定风速下,塔顶位移响应大于其他风速下的位移响应;高风速下,因叶片经变桨系统控制后,湍流风对塔顶位移响应影响程度降低,同时又因气动阻尼影响,地震激励导致的振动能量可以快速耗散。
(3)在地面加速度峰值为0.30g时,额定风速下塔架位移响应峰值最大;低风速下塔架加速度响应明显,而塔架位移、剪切力及弯矩响应峰值均较小;较高风速的湍流风会加剧塔架剪切力及弯矩响应峰值。
(4)湍流风与地震联合作用时,塔顶位移及剪切力和塔基剪切力及弯矩的临界地面加速度峰值随风速增大先增大再减小;塔顶加速度的临界地面加速度峰值在高风速下随风速增大而增大;塔顶弯矩受湍流风影响较大且地震激励作用对其影响不明显。
