大数据下基于IPSO优化模糊PSR-KELM模型预测风功率

任建龙 ，赵巧娥，严志伟，高金城

（1.山西大学 电力工程系，太原 030013；2.国网山西省电力公司检修分公司，太原030006；3.中国电缆工程有限公司，北京100079）

大数据是一种避免随机分析（即抽样调查）而采用所有数据进行处理的一种捷径[1]。如果我们通过分析全部的数据得到风力发电实际运行风速数据和输出功率数据之间的函数关系，并通过预测风速映射之后实现风力发电输出功率的预测，那么具有大数据4V特性的风力发电实际运行大数据势必会使我们投入大量的人力、物力以及时间，甚至最后都得不到准确的结果[2]。

研究风速、功率预测的文献很多，如文献[3]利用带有核函数的极限学习机（KELM）对风速预测，通过给定核函数的参数就可以避免由于随机设置初始权值造成极限学习机 （ELM）性能不稳定的问题，但是没有对核函数的参数进行寻优设置，导致最后的预测误差很大；文献[4]利用混沌学中的相空间重构（PSR）理论对风速进行预处理，然后再利用ELM预测风速，虽然考虑了风速数据空间及时间上的相关性，提高了预测精度，但是并没有考虑ELM初始权值随机设定造成ELM学习性能不稳定给最后预测精度带来的影响，也没有对相空间重构中的延迟时间τ和重构维数m进行寻优处理；文献[5]利用粒子群算法（PSO）对PSR理论中的延迟时间τ和重构维数m进行寻优处理，尝试寻找相空间重构参数和的优化值，但是并没有从全局考虑，很容易得到局部最优解；文献[6]利用PSO对正则化参数γ和核函数宽度σ进行寻优，再用KELM预测，虽然对核函数参数进行了优化处理，但是并没有考虑风速数据空间及时间上的相关性，也没有克服PSO容易陷入局部最优解这一缺点。本文考虑风电场实际运行数据异质值的存在，利用优化粒子群算法（IPSO）优化模糊PSR-KELM模型预测风速，同时提出改进移动平均平滑算法（IMASA）滤除异质值拟合风速-功率曲线。根据山西北部某风电场（简称晋北风场）的实际运行数据进行风速及功率的预测分析。

1 大数据下移动平均平滑算法的有效改进

大数据背景下的风力发电运维数据的主要特点是那些偏离正常运行主体数据的异质值会对风力发电的研究造成严重的影响，并不能被随意忽略或者删除[7]。

由于风的随机性、间歇性和不确定性，风电场的实际运行风速-功率数据可以看作是大量数据组成的波动序列｛ys（i）｝，其呈条带状分布在标准风速-功率曲线两侧[8]。为了方便研究，可将风电场视为一个输入风速、输出功率的简化系统[9]。

移动平均平滑算法（MASA）通过跨度内定义的相邻数据点的平均值代替每个数据点来平滑数据[10]。这个算法的通用表达如式（1）所示：

式中：ys（i）是第 i个数据的平滑值；N 是 ys（i）邻近数据点的个数；2N+1是跨度。

考虑到风电场实际运行数据异质值对拟合风速-功率曲线准确度的影响[11]以及MASA存在的不足，提出（IMASA），即为跨度内的数据点定义一个权重函数，通过权重函数值判断要平滑的数据点是否具有最大权重值以及对拟合曲线的影响程度。通过把跨度以外的数据点的权重值定义为零来避免异质值对拟合曲线准确度的影响，其数学表达如式（2）、式（3）所示：

式中：x是与数据点平滑相关的平滑值；xi是x通过跨度定义的最邻近数据点；d（x）是x沿横轴到跨度内最远的距离。

最后，利用最小二乘法将所得平滑值点拟合成一条映射曲线如式（4）所示：

总结以上算法，其原理流程如图1所示。

图1 拟合风速-功率曲线原理Fig.1 Principle of fitting wind speed power curve

2 IPSO优化模糊PSR-KELM模型

2.1 大数据下模糊C均值聚类算法的应用

在风速样本数据进行分组划分时，采用常规的K-means聚类算法虽然也能对风速样本数据进行分类划分，但是由于大数据下风速数据具有空间和时间相关性，对具有高相关性的风速数据进行聚类划分时，很容易产生不稳定的聚类结果，对准确划分风速数据具有一定的影响。模糊C均值聚类算法（FCM）能够有效地改善风速数据的空间和时间的相关性对最后聚类结果的影响，改善风速数据聚类划分结果的合理性。

FCM是经典聚类算法之一，它通过隶属度矩阵表示每个样本与各个分类之间的关系[12]，其原理如图2所示。

但是FCM也有不足的地方：①聚类中心随机选取，比较难确定，且聚类中心的选取对聚类结果影响很大；②容易得到次优解。可见，模糊C均值聚类算法虽然在风速预测中得到了应用，但仍需改进。

2.2 相空间重构理论

风电场不同机组采集的风速可以看作一组按照一定时间分辨率记录的多变量时间序列数值[13]，即：

式中：时间 t＝1，2，…，n；变量 i＝1，2，…，m；变量 vi（t）表示第i台风机在t时刻的捕获值。所以可将风电场不同机组捕获的风速数据记为一个m×n的多变量时间序列矩阵M，即

式中：t＝1，2，…，n（n 为时间点数）；i＝1，2，…，m（m为风机编号）；对M进行相空间重构，其空间中的相点可以表示为 vq，如式（7）所示：

2.3 核极限学习机

Guang-Bin Huang在2004年率先提出ELM，其实质是单隐层前馈神经网络（SLFN）学习算法的一种[14]。而以强大的非线性映射能力著称的核函数在处理非线性映射问题上具有很好的应用[15]。将Huang所提ELM隐含层结点映射用核函数等效代替，便可得到稳健性和非线性逼近能力更好的KELM。求解KELM 如式（8）、式（9）所示：

令ELM隐含层输出矩阵如式（10）所示：

从而可以将求解ELM写成式（11）：

令

那么基于核函数的ELM就可以用式（13）表示：

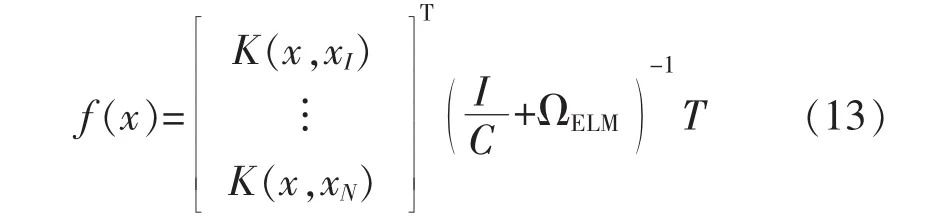
通常，工程上选取的核函数为高斯核函数，其数学表达式如下所示：

2.4 利用IPSO优化

针对Kennedy和Eberhart先前提出的PSO[16-17]在工程应用中存在搜索精度不高，容易陷入局部最优解等不足，本文率先利用IPSO克服以上算法存在的不足并应用到风速预测的实践当中[18]。粒子移动的下一时刻的速度如式（15）所示：

式中，vd′（t+1）表示任一粒子在维度d上下一时刻的速度；xd（t）表示任一粒子在维度d上t时刻的位置；w为惯性权重；pd（t）为任一粒子当前搜索到的最优解；pgd（t）为整个粒子群当前的最优解；c1、c2是可以改变 pd（t）和 pgd（t）相对重要性的学习因子；rand（）为随机数，取值一般在0～1之间。式（15）中常数能对惯性权重值、学习因子进行权衡，避免c1、c2过增，避免粒子更新偏向粒子局部或粒子整体，同时也避免了速度过增，使粒子群算法表现出更好地搜索性和收敛性还不增加计算量。粒子移动的下一位置为vd′（t+1）＝xd（t）+vd（t）。

2.5 程序框图

在利用IPSO进行优化时，以ARE作为衡量优化效果的标准。那么

为了降低程序迭代次数和计算量，设定寻优参数的约束条件如下所示：

最后，编写程序，利用IPSO进行优化处理。具体程序原理如图3所示。

3 实例验证

本文根据晋北风场现场实际运行数据进行实例分析。晋北风场位于山西盛风岭地区，总跨度约12.2 km，平均海拔在 1692～2120 m 之间，场址中心位于东经 114°～116°之间， 北纬 114°～116°之间，分为一、二期，共66台机组，总装机容量99 MW。由于该风电场位于山西以北典型山岭地带，所处地理环境复杂，综合考虑，该风电场的地理位置布置情况如图4所示。

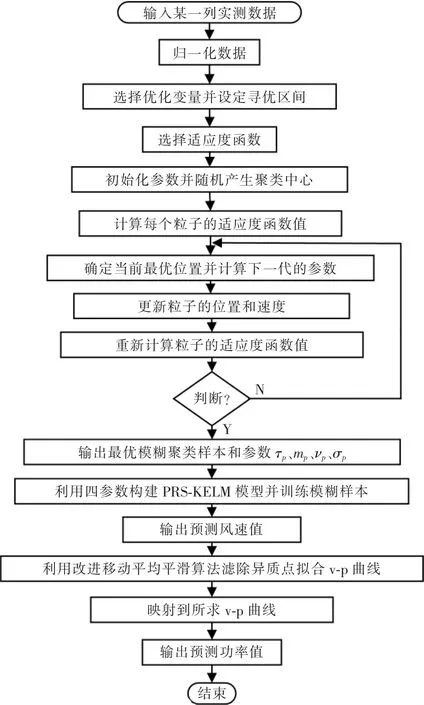
图3 IPSO优化模糊PSR-KELM模型预测风功率流程Fig.3 Flow chart of IPSO optimized fuzzy PSR-KELM model for predicting wind power

图4 晋北风场风机地理分布图Fig.4 Geographical distribution map of the north wind fan

晋北风场在不同时间段内的2个月实际运行风速-功率数据统计散点结果如图5所示。

图5 晋北风场实际运行风速-功率散点图Fig.5 Actual wind speed power dispersion diagram of Shanxi north wind field

本文以晋北风场10天的数据为例，根据晋北风场每10 min采集一次、总长度1440个的实际运行数据样本点进行实例分析，前十分之九的数据作为训练数据，后十分之一的风速数据作为测试数据。利用IPSO优化模糊PSR-KELM模型预测风速并将预测结果与实际运行数据、不同模型 （模糊PRS-KELM模型和PRS-KELM四参数优化模型）进行比较，如图6所示。

图6 不同模型的风速预测结果Fig.6 Wind speed prediction results of different models

将IPSO优化模糊PSR-KELM模型、不同模型（模糊PRS-KELM模型和PRS-KELM四参数优化模型）预测风速与实际运行数据进行比较，分析误差结果如图7所示。

图7 不同模型的风速预测误差分析结果Fig.7 Analysis results of wind speed prediction error of different models

将预测风速映射到利用IMASA滤除异质值后拟合的风速-功率曲线上预测功率并与MASA、不滤除异质值处理预测结果比较如图8所示。

图8 基于映射不同拟合曲线预测功率结果Fig.8 Predicting power results based on different fitting curves

利用式（16）计算晋北风场利用不同模型预测风速及功率的平均相对误差如表1所示。

表1 风速及功率的预测ARE值Tab.1 ARE value of wind speed and power

通过分析表1可以看出，基于IPSO优化模糊PSR-KELM模型预测风速的预测误差值较小，IPSO优化模糊PSR-KELM模型与模糊PRS-KELM模型和PRS-KELM四参数优化模型相比，精确度大大提高，说明IPSO优化模糊PSR-KELM模型的有效性。同时，预测功率误差说明IMASA滤除风电场实际运行风速-功率数据异质值的必要性和有效性。

4 结语

根据晋北风场的实际运行数据分析，利用PSR-KELM四参数优化模型训练IPSO优化模糊C均值聚类算法生成的模糊样本进行风速预测，克服了大数据下风电场实际运行数据中的异质值对风速预测模型准确度和稳定性的影响。另外，由于大数据下风电场运行数据异质值的存在，通过分析晋北风场实际运行数据发现，IMASA可以很好的避免异质值的影响并准确的拟合出一条基于实际运行数据的风电场风速-功率曲线。

另外，通过表1中不同模型对风速以及功率的预测误差对比还可以看出，利用本文提出的风功率预测模型完全可以对风电场出力变化趋势进行准确预测，并对风电场的运行并网目标实现可预测调控监视。