带通滤波器矩形系数的理论分析与仿真∗

胡保全 占腊民 陈长忠 李文广

（1.中航工业陕飞公司 汉中 723000）（2.华中科技大学 武汉 430074）

1 引言

带通滤波器在5G通信、雷达、导航定位、电子对抗、卫星通信等系统中发挥着非常重要的作用，具有极其广泛的应用价值［1～5］。理想情况下，工作频率位于滤波器通带内的信号通过滤波器时，插入损耗为零，而通带外频率的信号通过滤波器时则被完全衰减掉。具有这种幅频响应特性的滤波器称为“Brick Wall”响应滤波器。实际滤波器达不到这种理想情况。实际滤波器选择通带内有用信号，抑制带外干扰信号的能力，通常用矩形系数（Shape Factor，SF）来描述。该参数表征了带通滤波器幅频响应与理想矩形接近的程度。矩形度越高——即SF越接近理想值1，滤波器的选择性越好。高选择性滤波器是当前滤波器技术领域研究的热点之一［6～12］。

在滤波器技术领域，矩形系数与滤波器带宽、矩形系数与低通原型滤波器带外抑制之间的关系、决定矩形系数的影响因素等问题没有得到深入研究。有一部分从业者对带通滤波器的矩形系数理解不到位，甚至存在误解现象，极大地影响了带通滤波器的设计、选型和使用。

为解决此问题，本文依据低通原型滤波器和带通滤波器之间的频率映射公式，定量推导出矩形系数公式，揭示了带通滤波器矩形系数与带宽无关的规律，明确指出了带通滤波器矩形系数与低通原型滤波器带外抑制之间的关系，并对常用的Butterworth滤波器、Chebyshev滤波器矩形系数的影响因素进行了说明。在此基础上，应用ADS软件对上述结果进行了仿真验证。

2 带通滤波器矩形系数的理论分析

带通滤波器的矩形系数SF是其kdB带宽与3dB带宽的比值，k可取值30、40、50、60等。

式（1）中 BWkdB、BW3dB分别是带通滤波器k dB、3dB绝对带宽，ωUkdB、ωLkdB分别是k dB带宽的上边频、下边频，ωU3dB、ωL3dB分别是3dB带宽的上边频、下边频。

低通原型滤波器和带通滤波器之间的频率映射关系如式（2）所示［13］。

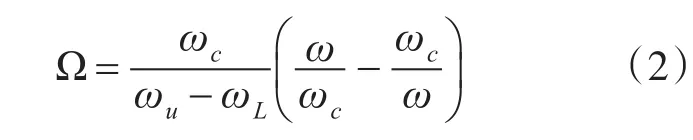
式（2）中 ωc、ωu、ωL、ω分别是带通滤波器角频率形式的中心频率、通带上边频、下边频、实际工作频率，Ω是归一化低通原型滤波器的工作频率。

依照式（2）定义的频率映射关系，可画出低通原型滤波器和实际带通滤波器的插入损耗-频率曲线。图1（a）、（b）是Butterworth滤波器幅频特性示意图。

由图1（b）可知，在实际带通滤波器插入损耗-频率特性曲线中，低于中心频率的部分是由低通原型滤波器的负频率映射而来的，高于带通滤波器中心频率的部分是由低通原型滤波器的正频率映射而来的。在这个映射过程中，低通原型滤波器和带通滤波器对应点的插入损耗保持不变。

在图1 b）中，带通滤波器BW3dB为Ω=1对应的ω=ωu和Ω=-1对应的ω=ωL之差，即

由式（2）可知，

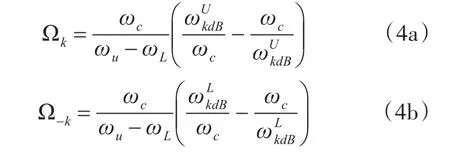
式（4）中，Ωk、Ω-k分别是带通滤波器k dB带宽上、下边频，ωUkdB、ωLkdB则是对应的低通原型滤波器工作频率。由式（4a）、（4b）可推导出

式（5）中，fbw为带通滤波器的相对带宽，即

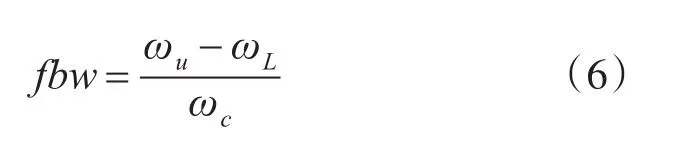
由（5）式可得带通滤波器的k dB绝对带宽为

由（3）、（7）式可知

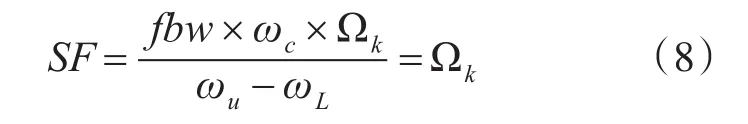
由式（8）可知，理论上带通滤波器k dB带宽对应的矩形系数，就是其等效低通原型滤波器幅频特性曲线在k dB和3dB衰减处的归一化频率的比值。矩形系数与带通滤波器的带宽无关。

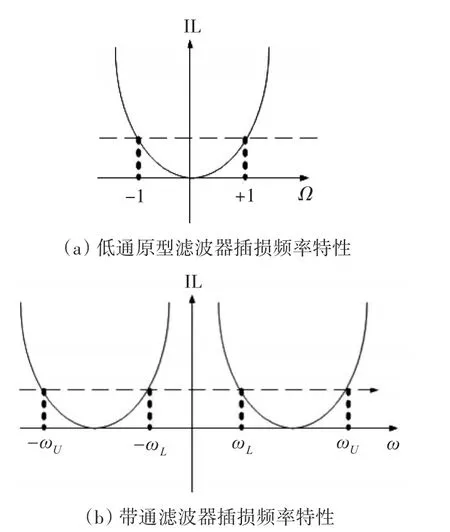
图1 Butterworth滤波器幅频特性示意图

要减小矩形系数，提高带通滤波器的矩形度，就得想办法减小低通原型滤波器k dB衰减处对应的归一化工作频率Ωk。对Butterworth低通原型滤波器而言，Ωk主要由滤波器阶数N决定。N越大，Ωk越小，矩形系数越小，矩形度越高。而Chebyshev低通原型滤波器的Ωk则受滤波器阶数N、通带波纹两者影响。N越大，通带波纹越大，Ωk越小，矩形系数越小，矩形度越高。

3 基于ADS的仿真验证

在ADS2014仿真环境中，先建立Butterworth、Chebyshev低通原型滤波器的原理电路图，并进行S参数线性仿真分析，再利用软件内置的BPF_Butterworth、BPF_Chebyshev模型，对带通滤波器的矩形系数进行仿真分析。

图2（a）为3阶Butterworth低通原型滤波器的幅频特性（g1=1，g2=2，g3=1），（b）为3阶3dB波纹的Chebyshev低通原型滤波器的幅频特性（g1=3.3487，g2=0.7117，g3=3.3487）。

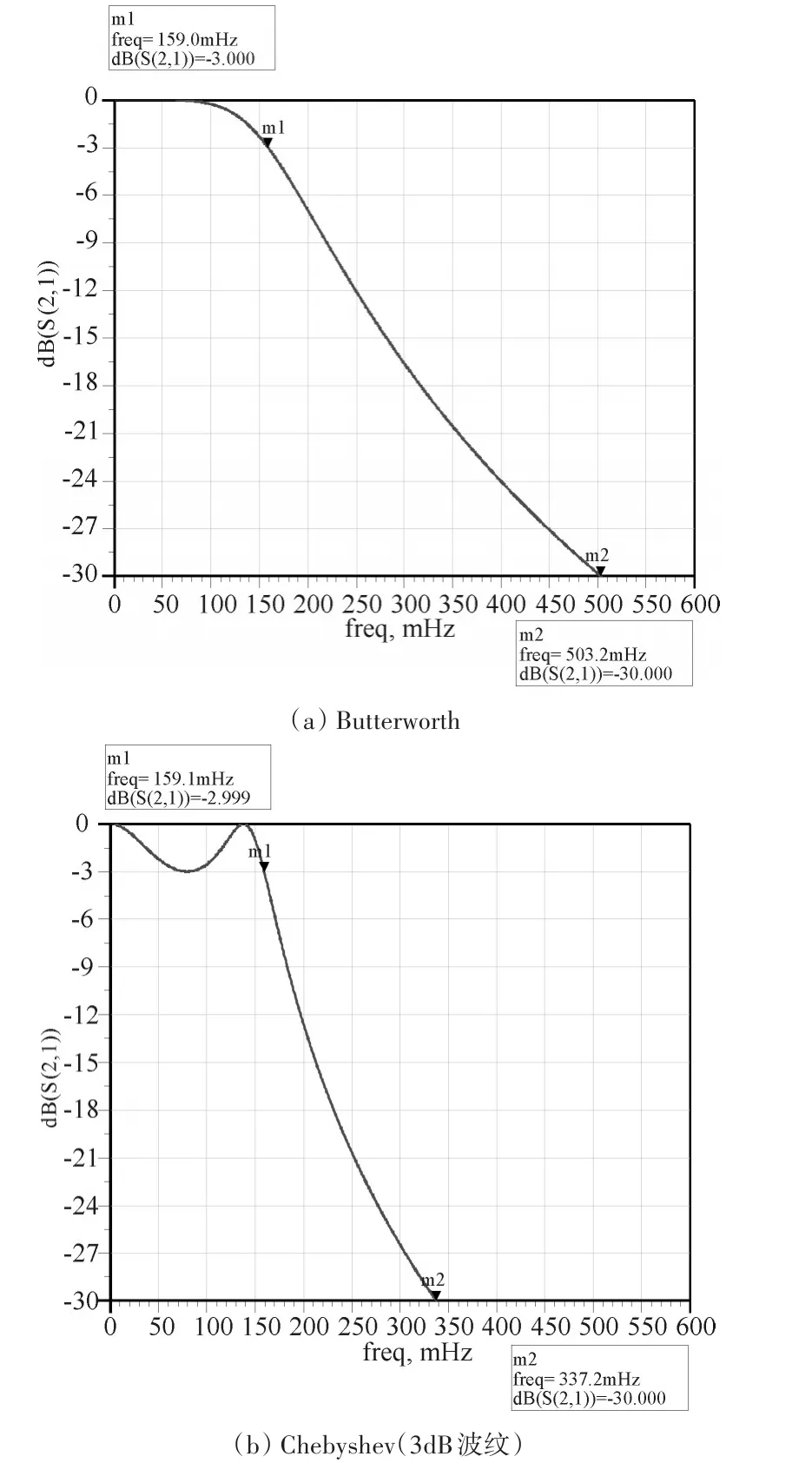
图2 低通原型滤波器幅频特性

由图2可知，3阶Butterworth滤波器在30dB和3dB衰减处的归一化频率比为3.2，3阶3dB波纹的Chebyshev滤波器相应的归一化频率比则为2.1。

在此基础上，利用ADS内置的BPF_Butterworth、BPF_Chebyshev模型，建立了3dB带宽分别为3%、10%的3阶Butterworth带通滤波器，和3dB带宽分别为3%、10%的3阶3dB波纹Chebyshev带通滤波器原理电路，并进行了S参数线性网络分析。最终得到的带通滤波器幅频特性曲线见图3、图4。

图3（a）中m1、m2、m3、m4和m5、m6、m7、m8标注的分别是3dB带宽为3%、10%的3阶Butterworth带通滤波器。m2和m1、m6和m5标注的频率差对应带通滤波器的3dB带宽，而m4和m3、m8和m7标注的频率差对应带通滤波器的30dB带宽。由这些数据，能计算出带宽为3%、10%的3阶Butterworth带通滤波器的30dB矩形系数均为3.2。这和图2（a）中Butterworth低通原型在30dB和3dB衰减处的归一化频率比3.2相同。

图3 带通滤波器的幅频特性

图3 （b）中m1、m2、m3、m4和m5、m6、m7、m8标注的分别是3dB带宽为3%、10%的3dB波纹Chebyshev带通滤波器。m2和m1、m6和m5标注的频率差对应带通滤波器的3dB带宽，而m4和m3、m8和m7标注的频率差对应带通滤波器的30dB带宽。由这些数据，能计算出带宽为3%、10%的3dB波纹Chebyshev带通滤波器的30dB矩形系数均为2.1。这和图2（b）中3dB波纹Chebyshev低通原型滤波器在30dB和3dB衰减处的归一化频率比2.1相同。

通过进一步的仿真分析发现，对Chebyshev带通滤波器而言，阶数相同时，波纹越大，矩形系数越小，矩形度越高。

表1 不同波纹下3阶Chebyshev带通滤波器的矩形系数

4 结语

由以上理论分析和仿真验证可知，理论上带通滤波器的矩形系数存在以下规律：

1）带通滤波器的矩形系数不受滤波器带宽影响；

2）带通滤波器k dB带宽对应的矩形系数，就是其等效低通原型滤波器幅频特性曲线在k dB和3dB衰减处的归一化频率的比值；

3）Butterworth滤波器的矩形系数主要由阶数决定，阶数越大，矩形系数越小，矩形度越高；

4）Chebyshev带通滤波器的矩形系数受滤波器阶数和波纹影响。阶数和波纹都大时，矩形系数小，矩形度高；通常情况下，滤波器阶数对矩形系数的影响要快于波纹对矩形系数的影响；

5）同等阶数下，Chebyshev带通滤波器的矩形系数比Butterworth带通滤波器的矩形系数小，矩形度相对较高。当Chebyshev带通滤波器的波纹小到一定程度，两种滤波器的矩形系数相当。

应该指出的是，调控滤波器的矩形系数时，滤波器的其他指标如插损、驻波等也会随之发生变化。实际应用时，需要结合滤波器性能指标要求综合考虑。

综上，本文所做工作深入揭示了带通滤波器矩形系数的概念及其变化规律，这对于带通滤波器的设计、选型和使用具有一定的指导意义和价值。