时标上局部耦合线性系统的聚类同步
2019-09-02李嘉敏宾红华黄振坤
李嘉敏,宾红华,黄振坤
(集美大学理学院,福建 厦门 361021)
0 引言
近年来,复杂网络同步性研究已经引起了学者们的广泛关注,并取得了丰硕的成果[1-4]。同时,衍生出了多种同步类型,如完全同步[1]、相位同步[2]、滞后同步[3]以及聚类同步[4]等。其中,聚类同步作为一种重要的同步现象,在信息科学领域有广泛应用,因而成为近年来一个新的研究热点。文献[4]首次考虑了线性耦合系统的聚类同步问题。随着对网络拓扑结构和聚类同步能力之间的深入研究与理解,研究者们逐渐提出了一些能够实现聚类同步的控制方法[4-7]。文献[7]通过间歇牵制控制方法研究了有向网络的聚类同步。另外,具有部分耦合状态的线性系统复杂网络同步问题也引起了控制领域学者的极大关注。为了使得网络达到聚类同步,不论节点间耦合强度如何,文献[8]提出了一种特殊的聚类间耦合方法。但是,对于在一般的耦合方式下达到聚类同步需要满足什么条件仍然未知。此外,聚类内部耦合强度下界以及同步速度也值得探讨。值得关注的是,文献[9]通过较为一般的牵制控制方法研究了线性系统有向网络的聚类同步问题,并且讨论了类内耦合强度下限与同步速度。
上述文献大都局限于连续情形,离散情况很少受到关注。因此在时标理论基础上研究聚类同步很有必要,它不但可以描述连续或离散情形,也可以描述连续和离散相混合的情形。Hilger提出的时标理论已经引起人们的关注并取得了很多成果[10-16]。但是,时标上的局部耦合线性系统聚类同步尚未得到研究。因此,本文将研究一般时标上具有部分耦合的线性系统有向网络聚类同步问题,运用牵制控制方法,分别讨论了固定拓扑和切换拓扑两种结构下线性系统有向网络达到聚类同步的充分条件。
1 预备知识
1.1 图论预备知识及模型描述
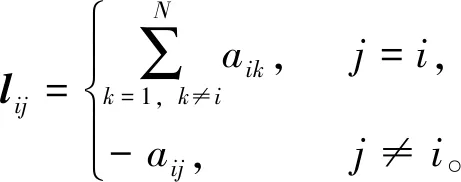
集合V={1,2,…,N}的一个集族{V1,…,Vq},其中V≠Ø,并且V∩Vk=Ø(≠k,,k=1,…,q),文中称V为类。令表示整数i所属子集的下标,即因此,如果i和j属同一类,则令G表示类V(=1,…,q)的拓扑结构,有V=V(G)。
考虑时标T上线性系统:
(1)
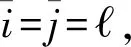
受到文献[5]和文献[17]中牵制控制方法的启发,本文设计了如下反馈控制器以实现系统聚类同步:1)选取齐次线性系统sΔ(t)=As(t)的q个特解s1(t),s2(t),…,sq(t),使其对任意,k=1,…,q,≠k,满足牵制控制器ui(t)设计为若节点i被牵制,则di>0,反之di=0。
1.2 相关定义及引理
时标T是实数集R的任意一个非空闭子集,如R,Z,N等。前跳算子σ:T→T,定义为σ(t)∶=inf{s∈T:s>t},并且当supT∈T时,σ(supT)=supT。后跳算子ρ:T→T定义为ρ(t)∶=sup{s∈T:s
定义1[11]设f:T→R,t∈Tk。若存在fΔ(t),对任意ε>0,存在t的邻域U∈T,使得|(f(σ(t))-f(s))-fΔ(t)(σ(t)-s)|≤ε|σ(t)-s|,∀s∈U,则称它为f在t处的Δ-导数。若fΔ(t)在所有t∈Tk均存在,则称f是Δ-可微的。
对任意的t∈Tk,可得f(σ(t))=f(t)+μ(t)μfΔ(t)。若f,g是两个可微函数,则fg的导数为(fg)Δ=fΔg+fσgΔ=fΔgσ+fgΔ。
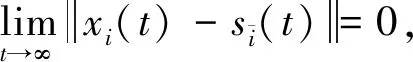
L表示含有N个节点的非负加权有向图G的Laplacian矩阵,D=diag{d1,…,dN}是非负对角阵。令G表示包含有向图G,节点0,以及从0到图G中的有向边(当且仅当di>0则从节点0到节点i∈{1,2,…,N}之间存在有向边连接)的有向图。因此,从文献[18-19]中得到引理1。
引理1[9]L和D如上所述,则:1)若图G平衡,
(L+LT)/2+D>0,
(2)
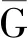
Ξ(L+D)+(L+D)TΞ>0
(3)
成立。
注1 引理1给定任意非负加权有向图G以及非负矩阵D=diag{d1,…,dN},找寻满足式(3)矩阵的方法,文献[17]定理1已做出了详细说明。
引理2 Kronecker积⊗有如下性质:1)(αΦ)⊗Ψ=Φ⊗(αΨ);2)(Φ+Ψ)⊗P=Φ⊗P+Ψ⊗P;3)(Φ⊗Ψ)(P⊗Γ)=(ΦP)⊗(ΨΓ);4)(Φ⊗Ψ)T=ΦT⊗ΨT。
引理3 对任意列向量x∈Rmn,有:xT(Q⊗W)x≤λmax(Q)xT(Im⊗W)x,xT(W⊗Q)x≤λmax(Q)xT(W⊗Im)x,其中Q∈Rm×m是对称矩阵,W∈Rn×n是对称半正定矩阵。
引理4 令C1,C2是N×N阶Hermitian矩阵,则满足λmin(C1+C2)≥λmin(C1)+λmin(C2)。
假设1 矩阵对(A,B)稳定,并且∑j∈V(G)aij=0,∀i=1,2,…,N,i∈VVG。若矩阵对(A,B)稳定,那么对任意正数δ,下列Riccati不等式存在解P>0,使得:
PA+ATP-δPBBTP+δIn<0。
(4)
2 固定拓扑下的聚类同步
本节主要研究在固定拓扑结构下系统达到聚类同步的条件。为了便于分析,记每类中的节点数量为n(1≤≤q),显然,N=n1+…+nq。Laplacian矩阵以下列形式给出:其中Lii由图Gi决定,Lij表示类Gj到Gi(i,j=1,…,p)的信息传送,入度平衡条件等价于矩阵L(≠k,,k=1,…,q)满足列和为零。
令D=diag{D1,…,Dq}=diag{d1,…,dN},其中D∈Rn×n(=1,…,q)。矩阵D描述类V中的节点牵制情况。此外,令
(5)
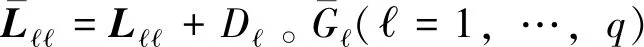
(6)
文中,记L0=L-diag{L11,…,Lqq}≥0和Ξ=diag{Ξ1,…,Ξq},显然L0只与不同类间的耦合强度有关,而与类内耦合强度c(=1,…,q)无关。
定理1 在假设1下,若每一个类中均有节点被牵制,使得每个G(=1,…,q)都包含有向生成树,则:对于固定的q个数组(c1,c2,…,cq)(c>0,=1,…,q),通过选定K=BTP使线性系统(1)能够以φ/(2λmax(P))的速率指数型达到聚类同步,其中φ=mint∈T{η1+μ(t)(η2-η3λmax(Σ))}>0,P>0是不等式(4)和
ATPA+(η4-η1)ATPBBTP-η4PBBTPA+η2In<0
(7)
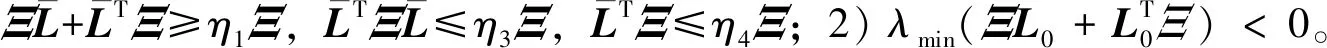
(8)
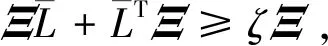
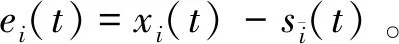
(9)
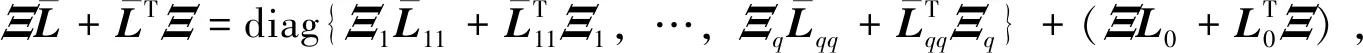
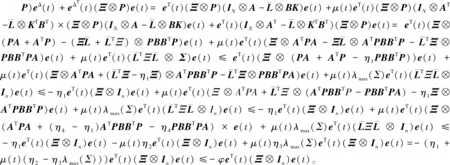
由V(t)≤λmax(P)eT(t)(Ξ⊗In)e(t)可知,VΔ(t)≤-φV(t)/λmax(P)。因此,系统(1)可以φ/(2λmax(P))速率指数型达到聚类同步。
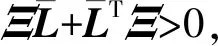
(10)
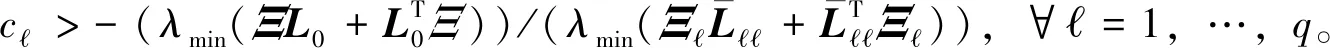
注2 根据定理1可知,除了矩阵对稳定和一定的连通性假设之外,只要类内的耦合强度与不同类之间强度相比足够强,那么系统就可快速达到聚类同步。此外,定理1还得到了确保系统达到同步的类内耦合强度下界,采用的牵制方案允许任意的类内拓扑结构且不需要其他连通条件。
3 切换拓扑下的聚类同步
本节讨论切换拓扑下的同步问题。t时刻的网络拓扑图记为G(t),其中G1(t),…,Gq(t)分别为q类{V1,…,Vq}的网络拓扑图,线性系统模型如下:
(11)
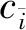
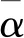
假设2 任意t时刻,矩阵L(t)(k≠)均满足列和为零。
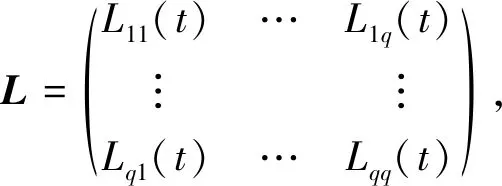
(12)
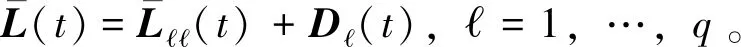
对每一类V,定义
(13)
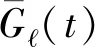
令
(14)
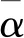
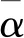
定理2 在假设1和假设2下,若每个G(t)是平衡图且每一类中均有节点被牵制使得保持弱连通,则有:对于固定的q个数组(c1,c2,…,cq)(c>0,=1,…,q),通过设计反馈矩阵K=BTP,使得线性系统(11)以速率φ/(2λmax(P))达到聚类同步,其中φ=mint∈T{γ1+μ(t)(γ2-γ3λmax(Σ))}>0,P>0是不等式(4)和
ATPA+(γ4-γ1)ATPBBTP-γ4PBBTPA+γ2In<0
(15)
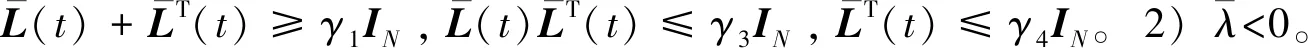
(16)
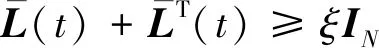
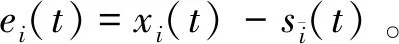
(17)
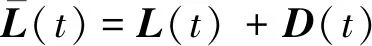
(18)
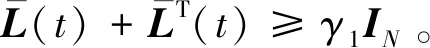
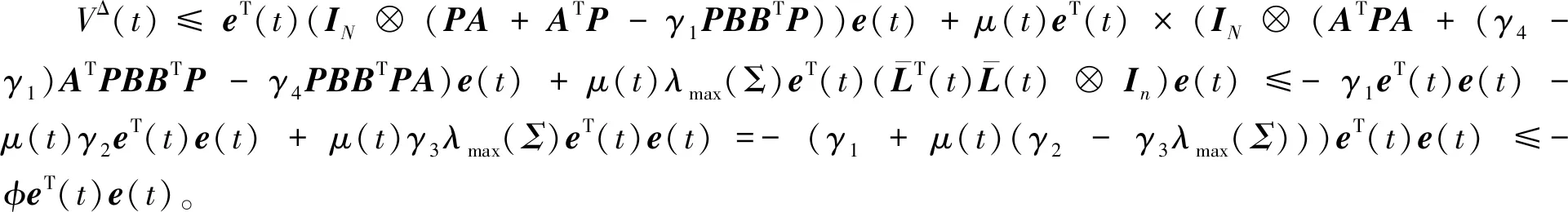
4 数值模拟
为了验证以上理论分析,给出一组参数进行数值模拟。
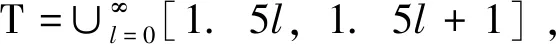
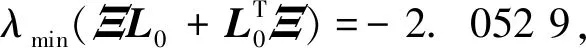
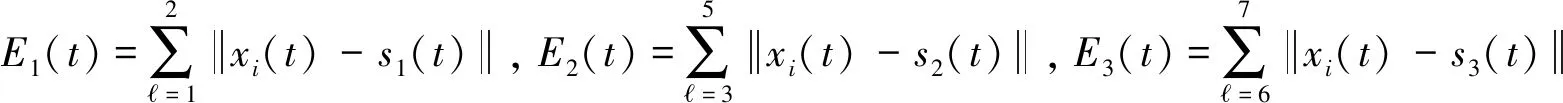
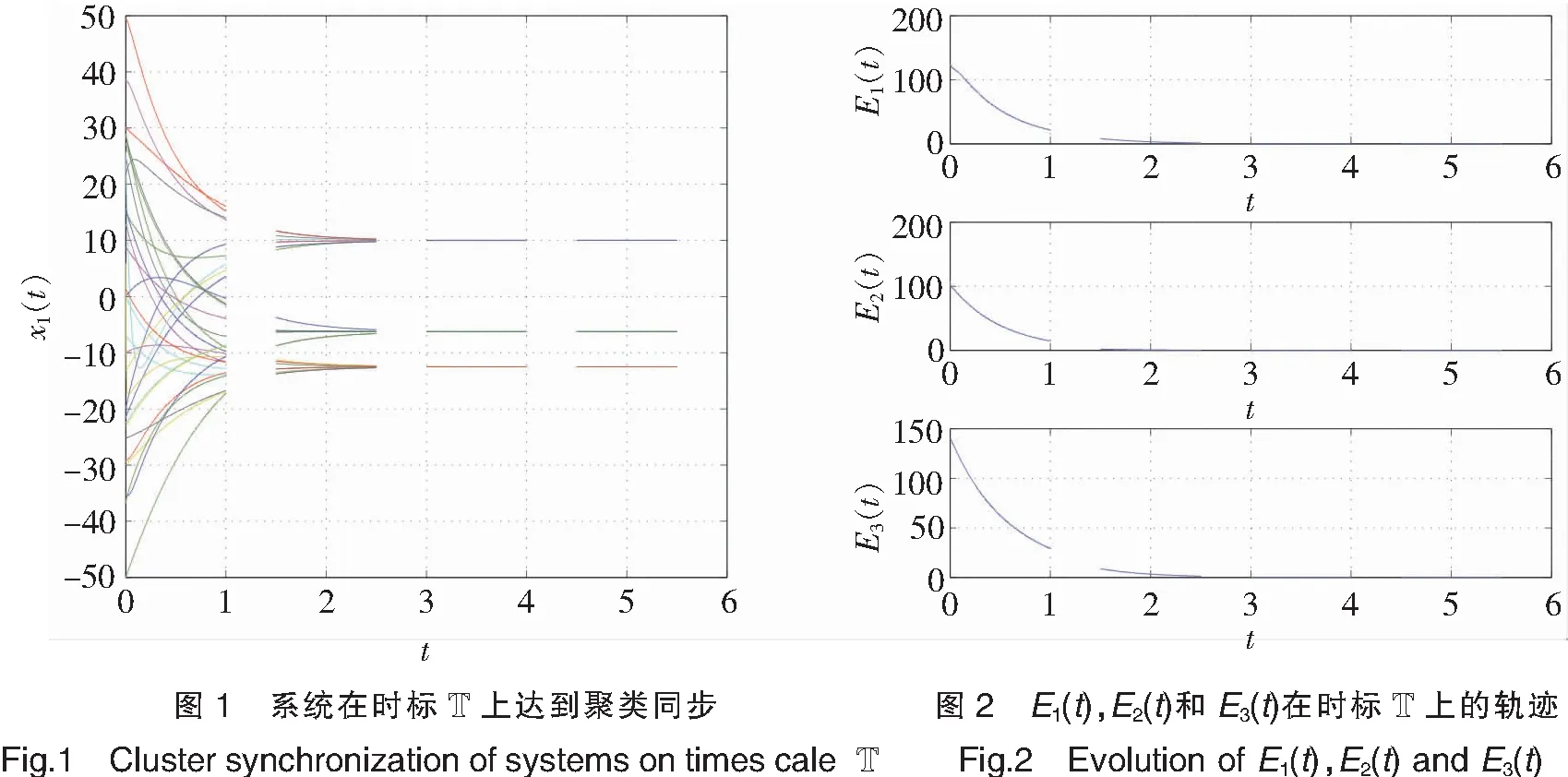

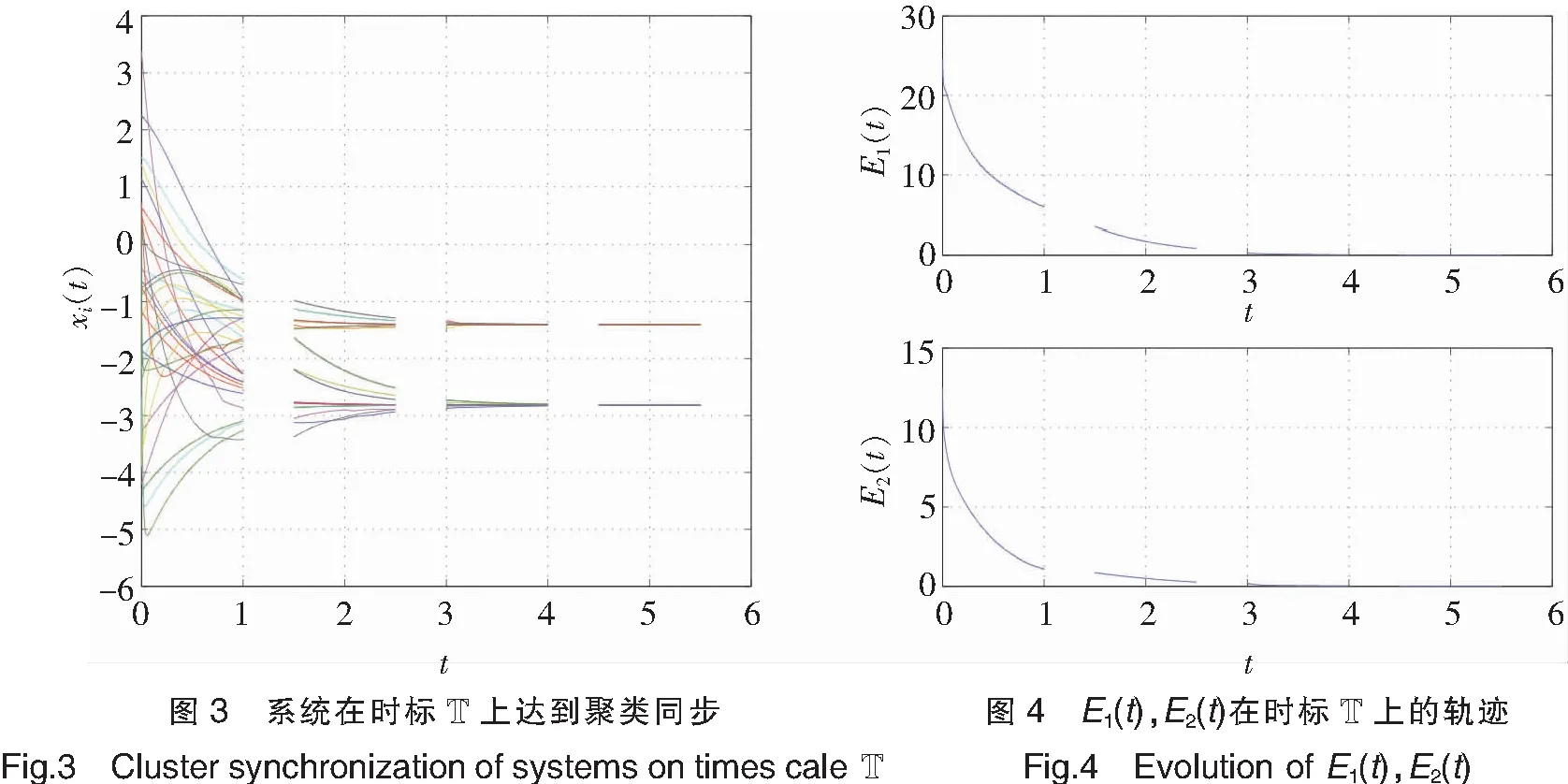
在上述算例中,若时标T=R,则距离函数μ(t)≡0,此时本文的结果和文献[9]类似,因此本文所得结果不仅包含文献[9]连续情况下的结果,还包含了连续与离散混合情况,是对文献[9]的一种推广和拓展。上述数值算例表明本文结论正确,比文献[9]结果更具有一般性。
5 结语
通过牵制控制策略,研究了一般时标上节点之间具有局部耦合状态的线性系统网络聚类同步。在固定拓扑结构下,本文结果表明,可设计合适的反馈矩阵来达到聚类同步,只要网络满足2点:第一,每个聚类的诱导网络拓扑结构具有有向生成树;第二,类内的耦合强度与不同类之间强度相比足够强。此外,若要求每个聚类诱导网络拓扑是平衡图,那么结果可拓展到切换拓扑的情形。本文还取得了保证达到聚类同步的类内耦合强度下限以及聚类同步的速率。
