采用五棱镜扫描法检测大口径平面镜的面形

袁 理，张晓辉

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033;2.中国科学院大学，北京 100049)

1 引 言

大口径平面镜通常是指口径大于1 m的平面镜。大口径平面镜在空间光学、天文光学等领域有着大量应用。为了确保大口径平面镜具有良好的质量，必须对其面形进行检测。大口径平面镜面形的检测方法主要有4种：直接干涉检测法[1]、Ritchey-Common法[2-3]、子孔径拼接法[4-7]和五棱镜扫描法[8-15]。直接干涉检测法需要一块高精度的大口径标准平面镜，该镜的加工难度很大，成本极高，因此该方法并不适用。Ritchey-Common法需要一块高精度的大口径标准球面镜，成本也较高，并且由于光束是斜入射到平面镜上的，所以光路搭建和调整也比较困难。子孔径拼接法可以避免使用大口径标准镜，但是该方法的误差累积现象比较严重，并且检测时间较长，易受环境影响，所以检测精度不是很高。五棱镜扫描法通过测量表面倾斜角检测大口径平面镜的面形，不需要使用大口径标准镜，成本较低，通过适当地设计算法和检测流程，可以有效抑制各种主要误差的影响，检测精度较易保证，是一种比较好的方法，也是本文所研究的方法。

国内外研究人员提出了一系列不同的五棱镜扫描法，大体上可分为两种类型。第一种五棱镜扫描法[8-12]是使用一个扫描的五棱镜来直接测量表面倾斜角，这种方法受各种误差的影响都较大，不宜采用。第二种类型的五棱镜扫描法[13-15]是使用两个五棱镜来测量表面倾斜角的差值，其中一个是静止的参考五棱镜，另一个是运动的扫描五棱镜；该方法可以消除倾斜误差的一阶影响和大部分环境的影响，但是由于两个五棱镜具有不同的制造误差，所以五棱镜制造误差的影响不能在作差的过程中消除，因此该方法也有缺陷。另外，这两种方法在扫描过程、算法等方面也各有一些不足。

针对上述问题，本文提出了一种新的五棱镜扫描法，与以前的方法相比，主要有以下改进：第一，使用一个扫描的五棱镜来测量表面倾斜角的差值，可以消除倾斜误差的一阶影响、五棱镜制造误差的影响和大部分环境的影响；第二，增加了一套反馈控制系统，用于自动监视和减小五棱镜在扫描过程中的倾斜变化量；第三，对于两个配对点，测量时间紧邻着，而不是按照各点的排列顺序依次测量，有利于减小环境变化的影响；第四，使用Zernike多项式来表示被测面形，然后建立超定方程组，通过最小二乘算法，直接得到二维面形，而不是先测出一维面形再进行拼接，不但减少了计算量，而且避免了拼接误差。这些改进可显著提高检测的精度和效率。

2 检测原理

2.1 表面倾斜角差值的测量

表面倾斜角测量原理图如图1所示。

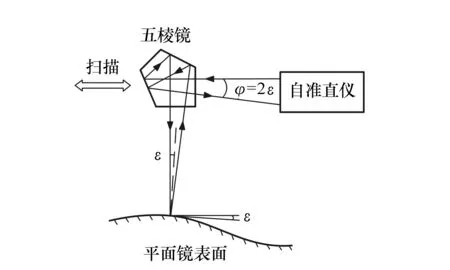
图1 表面倾斜角ε测量原理示意图 Fig.1 Measurement schematic of the tilt angle ε of surface

如图1所示，自准直仪发出的光束被五棱镜偏转90°后入射到平面镜上，经平面镜反射后再经过五棱镜回到自准直仪，自准直仪可测出光束的偏转角度φ，则平面镜在扫描方向上的表面倾斜角ε等于：

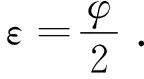
(1)

五棱镜具有优良的误差抑制特性，五棱镜的倾斜误差对ε的测量值仅产生很小的二阶影响[16]。然而，自准直仪的倾斜误差、被测平面镜的整体倾斜误差、五棱镜的制造误差以及环境带来的误差却对ε的测量值影响很大，但是，如果将两个点处的ε值作差，则可以有效抑制这些误差的影响。在五棱镜扫描过程中，设自准直仪在两个点处的读数分别为φ1和φ2，测得的表面倾斜角分别为ε1和ε2，则这两个点的表面倾斜角的差值δ等于：

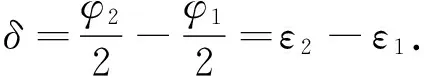
(2)

图2为自准直仪存在倾斜角ω时的测量示意图。

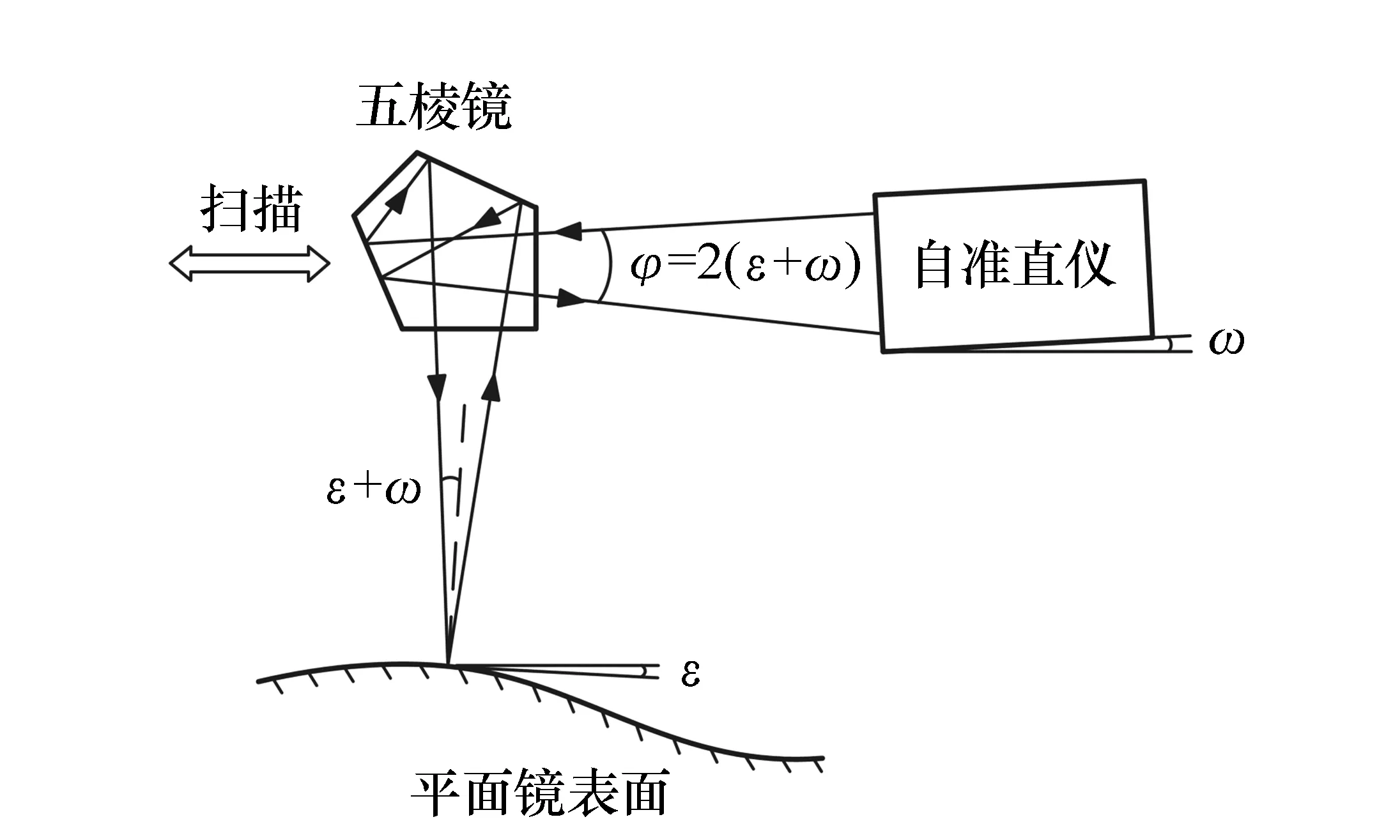
图2 自准直仪存在倾斜角ω时测量示意图 Fig.2 Measurement schematic when autocollimator has a tilt angle ω

如图2所示，如果自准直仪存在ω角的倾斜误差，则自准直仪在这两个点处的读数φ1和φ2变为：

φ1=2(ε1+ω),φ2=2(ε2+ω) .

(3)

在五棱镜扫描过程中，自准直仪是不动的，所以ω角不变，于是得到表面倾斜角的差值δ等于：

(ε1+ω)=ε2-ε1.

(4)

可见，式(4)与式(2)的结果是相同的，自准直仪的倾斜误差ω在作差的过程中抵消掉了，从而对δ不产生影响。类似地，被测平面镜的整体倾斜误差、五棱镜的制造误差以及大部分环境带来的误差也在作差的过程中抵消，详见第4节的误差分析。

2.2 扫描方式

首先定义两种距离d和D。将作差的两个点称为“配对点”。如图3所示，假设在某一条扫描直线上有6个测量点，其中第1点和第4点配对作差，第2点和第5点配对作差，第3点和第6点配对作差，则将d称为“两个配对点的距离”，将D称为“点对的距离”。D实际上就是采样间距。

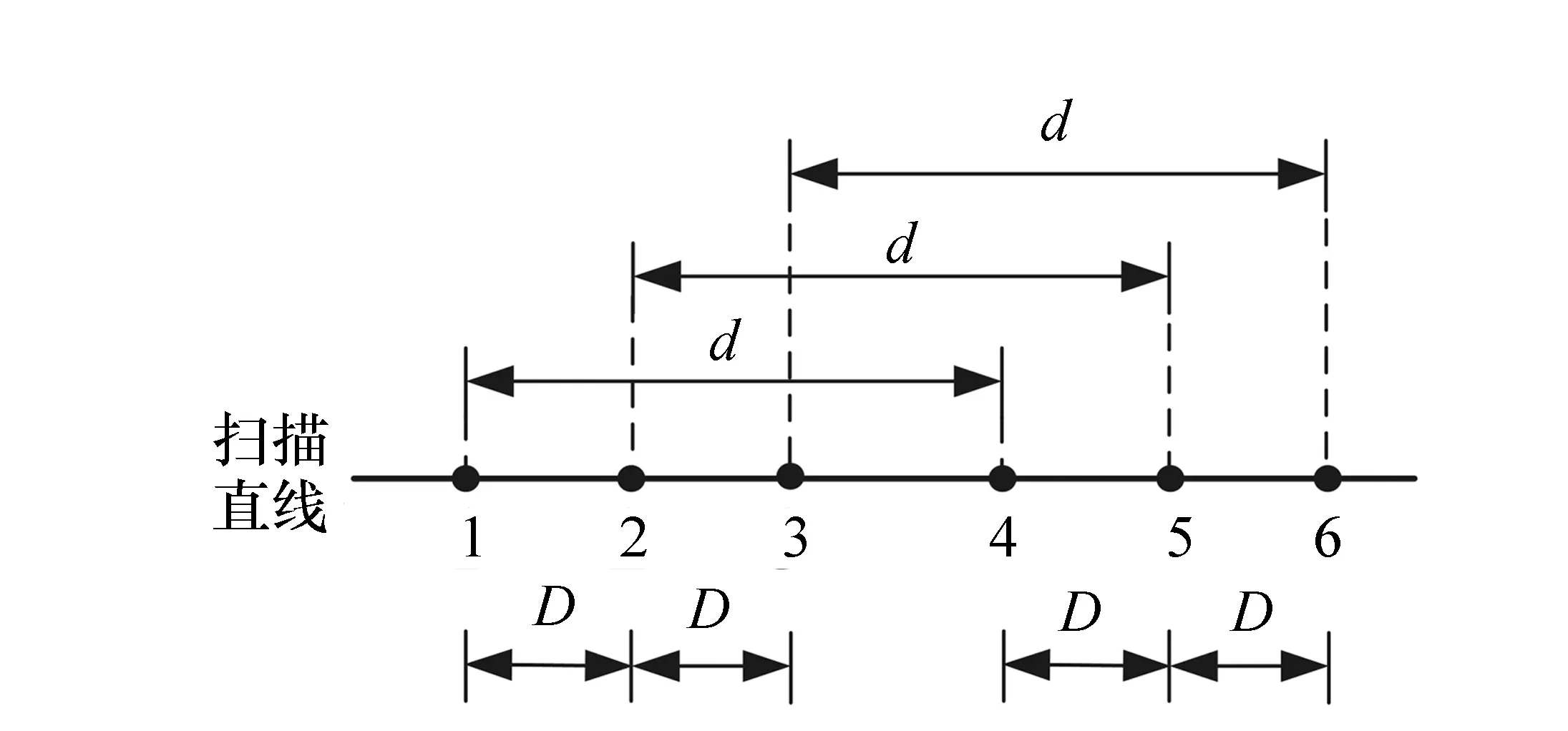
图3 距离d和D的定义 Fig.3 Definitions of the distances d and D

需要注意的是，对两个配对点的测量有一段时间间隔，如果在这段时间间隔里环境发生了变化，那么在作差时，环境的影响就不能完全抵消。所以，要尽量减小两个配对点测量时间的间隔，以减小环境变化的影响。因此需要做到以下两点：第一，对两个配对点的测量必须在时间上紧邻着，例如，如图3所示，测量的顺序应该是1、4、2、5、3、6，而不能是1、2、3、4、5、6；第二，五棱镜的运动速度要尽量快，距离d不能太大，以减少五棱镜在两个配对点之间的运动时间。另外，距离d也不能太小，如果d太小，则表面倾斜角的差值δ就会很小，在绝对误差不变的情况下，相对误差就会很大。在充分考虑这些因素后，在本文的实验中，d取150 mm，五棱镜的运动速度为20 mm/s，运动时间为7.5 s。

扫描路径如图4所示，采用极坐标扫描路径，共扫描20条直线，所有扫描直线交汇于被测平面镜中心。相邻扫描直线之间的夹角为π/20，而被测平面镜的直径为1.5 m，因此其边缘的采样间距等于750 mm×π/20≈120 mm，在被测平面镜的中心，采样间距接近于0，所以平均采样间距为120 mm/2=60 mm，相应地，点对的距离D也取60 mm。这样，每条半径上测量11对配对点，共测量440对配对点。另外，采样口径取27 mm。

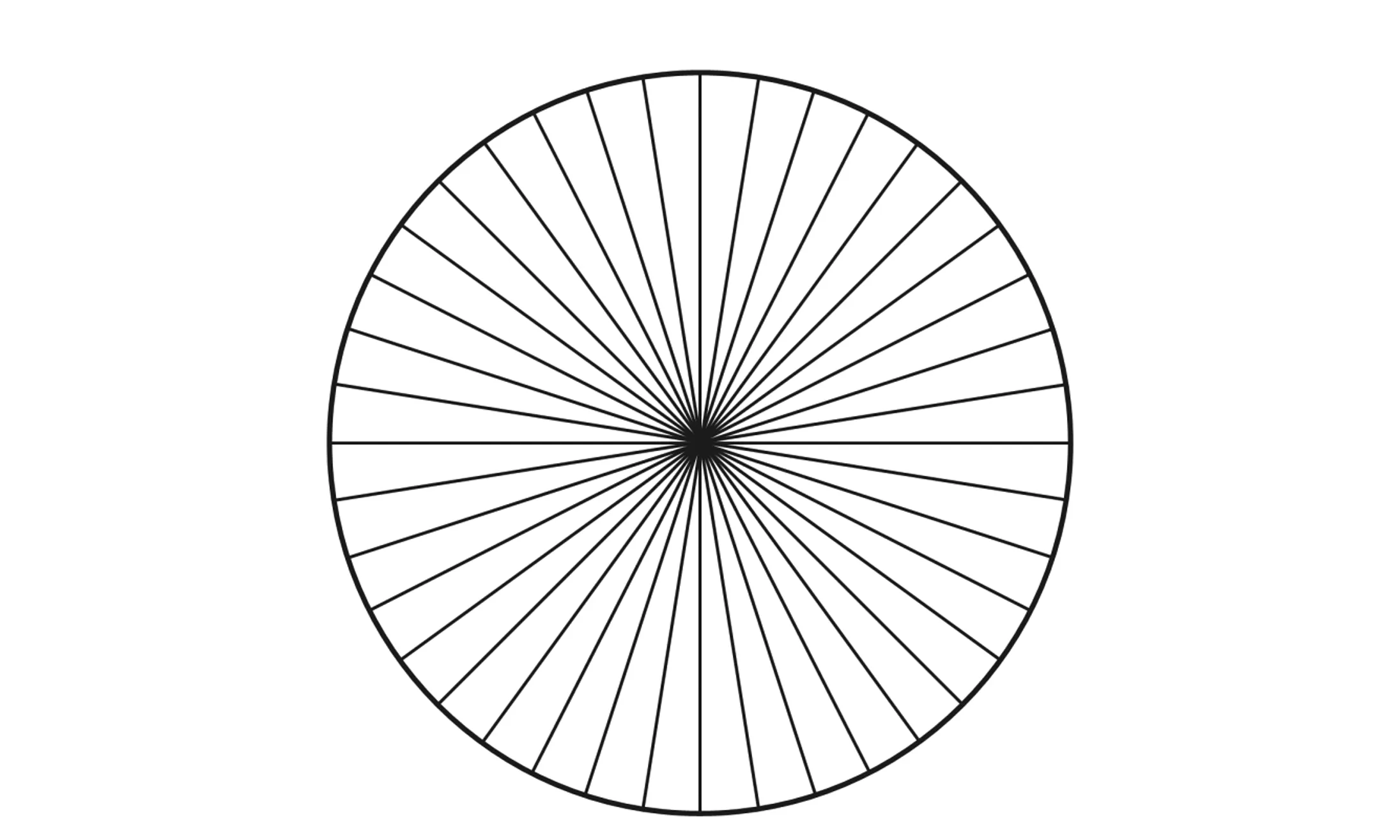
图4 扫描路径 Fig.4 Scanning paths

2.3 被测平面镜面形的计算

在柱坐标系下，将被测平面镜的面形S(ρ,θ)表示为Zernike多项式Zi(ρ,θ)[17]的线性组合如下：

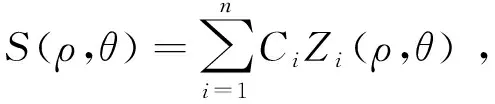
(5)

其中：n为Zernike多项式的项数，在本文中n取36；Ci为各项Zernike多项式的系数。由于Zernike多项式是定义在单位圆上的，所以有0≤ρ≤1。

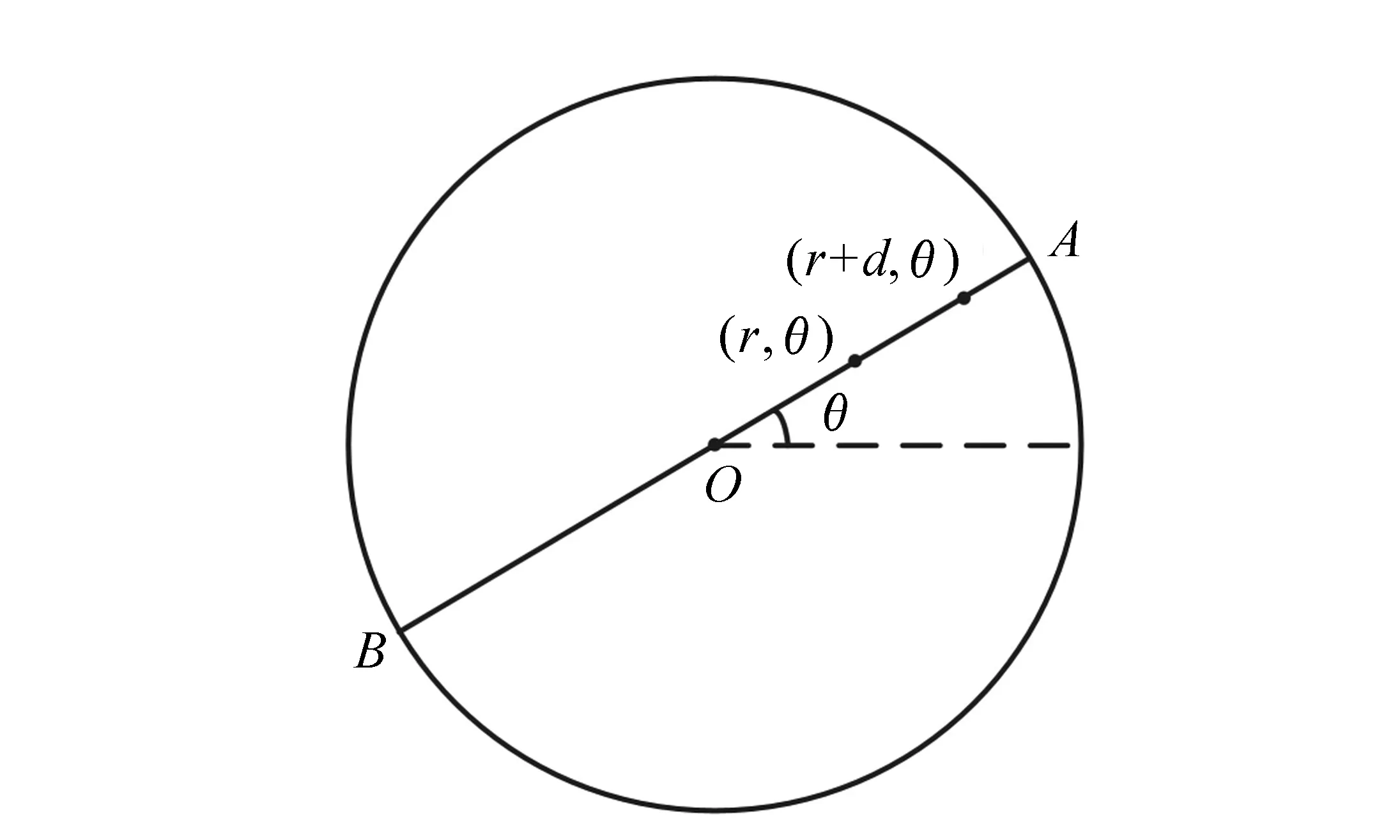
图5 两个配对点的极坐标 Fig.5 Polar coordinates of two matching points

设某一条扫描直线AOB上有两个配对点，它们到中心O的距离分别为r和r+d，极坐标分别为(r,θ)和(r+d,θ)，如图5所示。将它们的极径归一化为ρ1和ρ2：

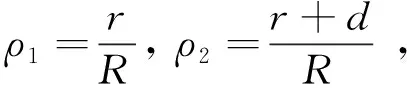
(6)

其中：R是被测平面镜的半径。设这两个配对点的表面倾斜角为ε1和ε2，由于ε1和ε2是沿径向方向的，并且都比较小，所以得到：

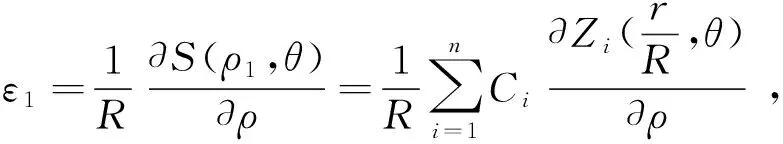
(7)

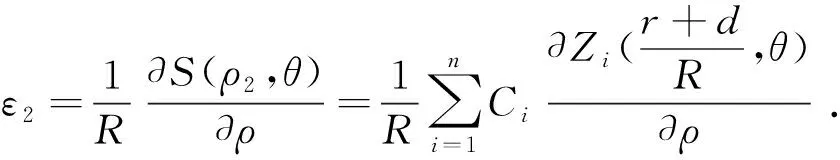
(8)

由于作了极径的归一化，使得被测平面镜的半径从R缩小为1，这样，各点的斜率实际上就变为了原来的R倍，因此需要在式(7)和式(8)的右端乘以1/R。将(8)式和(7)式相减，得到表面倾斜角的差值δ等于：

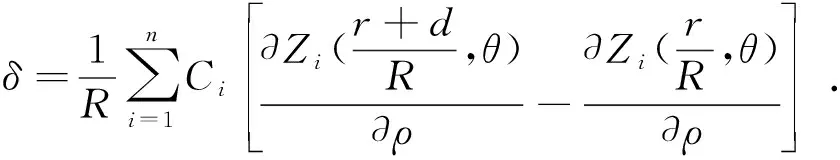
(9)

在式(9)中，只有Ci是未知的。每测量一对配对点，都可以根据式(9)得到一个关于Ci的方程，在测量完所有配对点后，就可以得到关于Ci的超定方程组，然后通过最小二乘法就可以求出Ci，再根据式(5)就可以得到被测平面镜的面形表达式。

在检测过程中，还需要注意以下两点：第一，在同一条扫描直线上，在中心O的两侧，表面倾斜角的正方向是相反的；第二，两个作差的配对点必须位于同一条扫描直线上，并且位于中心O的同一侧，即它们必须具有相同的极角θ，只有这样才能在作差时抵消掉所有的一阶倾斜误差。

2.4 五棱镜倾斜变化量的自动监视与调整

为了监视五棱镜在扫描过程中的倾斜变化量，在检测系统中增加了一个自准直仪和一个返回平面镜。如图6所示，自准直仪1与五棱镜用于测量表面倾斜角，增加的自准直仪2与返回平面镜用于监视五棱镜的倾斜变化量。五棱镜和返回平面镜安装在同一个底座上。

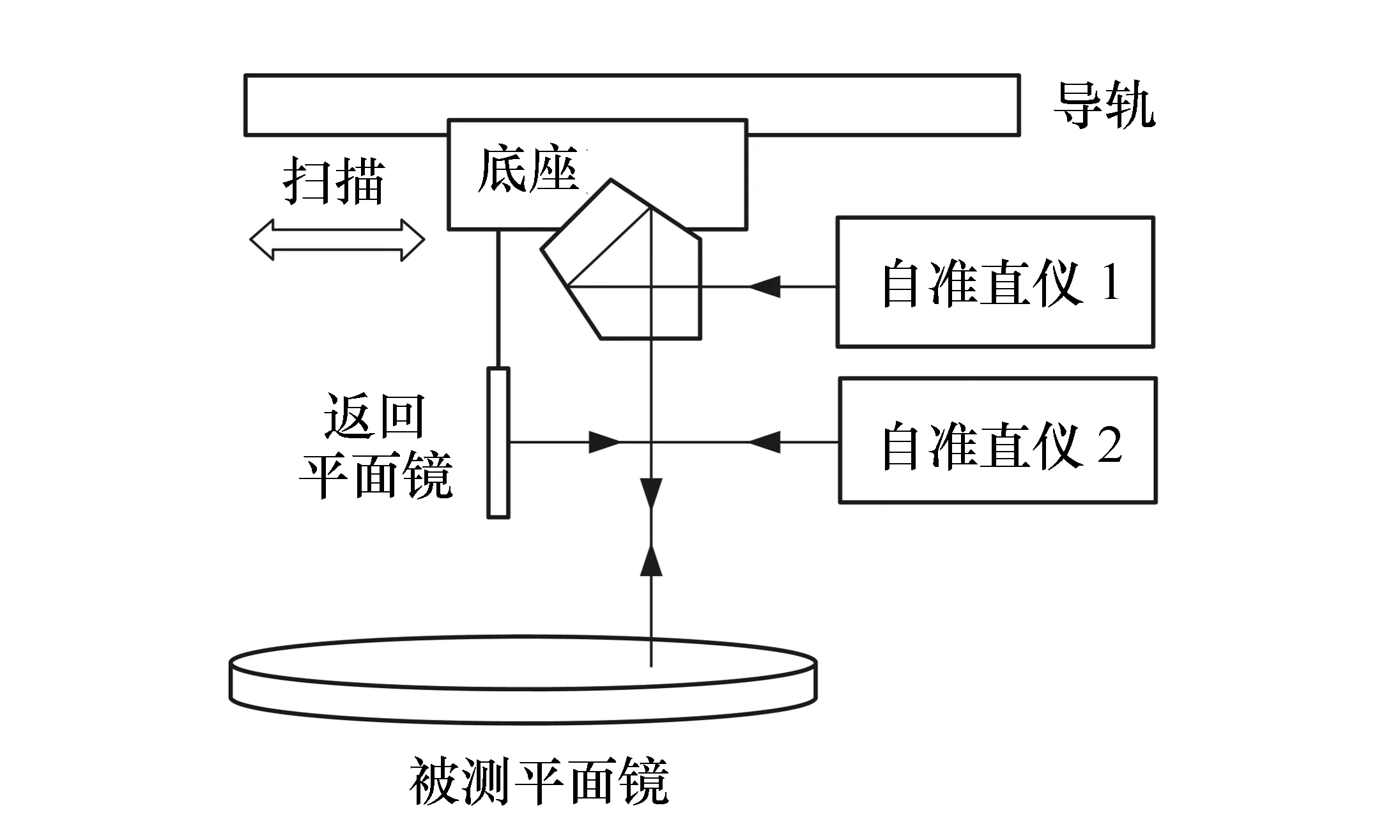
图6 自准直仪2和返回平面镜监视五棱镜的倾斜变化量示意图 Fig.6 Schematic of using autocollimator 2 and the return mirror to monitor the changes of pentaprism tilts

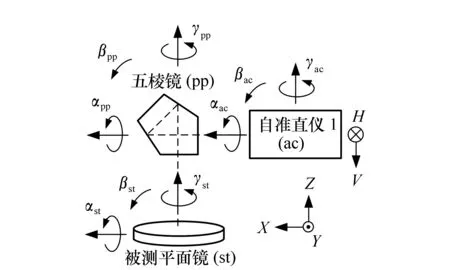
图7 各个光学组件的倾斜角 Fig.7 Tilt angles of the optical components

图7画出了各个光学组件的倾斜误差角，α、β和γ分别表示绕X轴、Y轴和Z轴的倾斜误差角，下标ac、pp和st分别表示自准直仪1、五棱镜和被测平面镜。注意，βst由两部分组成，一是被测平面镜的整体倾斜，二是被测平面镜局部的表面倾斜，αst也一样。

V和H分别表示自准直仪1在两个方向上的读数值的一半，V实际上就等于式(1)中的ε加上一些误差项。通过光路追迹，可以得到V和H等于[18]：

αst(αpp+γpp)-βst+βac+V0，

(10)

H=βst(αpp+γpp-γst-αac)+

αst-αpp+γpp-γac+H0.

(11)

在以上两式中，角度的单位必须是弧度，典型的换算关系为1 μrad等于0.2″。V0和H0是两个常量，来源于五棱镜的制造误差。现在用Δ来表示相对于扫描前的变化量。忽略式(11)中很小的二阶项，得到H的变化量ΔH等于：

ΔH=Δαst-Δαpp+Δγpp-Δγac+ΔH0.

(12)

在五棱镜扫描过程中，自准直仪1是不动的，所以Δγac=0；H0是一个常量，所以ΔH0=0；对于抛光后的平面镜，Δαst大致在3 μrad rms左右，而在本系统中，五棱镜在扫描过程中的倾斜变化量Δαpp和Δγpp大致在60 μrad rms左右。可见Δαst远小于Δαpp和Δγpp，所以忽略(12)式中的Δαst，得到：

Δαpp=Δγpp-ΔH,

(13)

其中，Δγpp可由自准直仪2测得，ΔH可由自准直仪1测得，于是根据式(13)即可求出Δαpp。获得Δγpp和Δαpp的值后，就可以通过反馈控制和自动调整来减小它们。一般可以将Δγpp和Δαpp减小到15 μrad rms以内，实际上就减小了倾斜误差的二阶影响。

注意，Δβpp对检测无影响，因此无需对它进行监视与调整；另外，在每个测量点处，必须在测量表面倾斜角以前完成监视与调整。

2.5 检测原理的仿真分析

为了验证检测原理的正确性，按照2.2节中所述的参数，对检测原理进行了仿真分析，计算软件采用MATLAB。仿真分析步骤如下：第一步，假设出任意36个Zernike多项式系数的真值，得到被测平面镜的真值面形；第二步，利用Zernike多项式系数的真值，按照式(9)计算出440个表面倾角差值的真值，然后利用这些表面倾角差值的真值，按照2.3节的方法计算出Zernike多项式系数的仿真值，得到仿真面形；第三步，将仿真面形与真值面形作差，得到面形复原误差，再计算该面形复原误差的rms值。

按以上步骤重复计算10次，得到10个rms值，它们的最大值仅为2.3 nm rms，可见检测原理是正确的，原理误差为2.3 nm rms。

3 检测系统

图8 检测系统 Fig.8 Measurement system

检测系统如图8所示。五棱镜和返回平面镜安装在同一个底座上，底座上有倾斜自动调整机构。底座可在两根长度为2.2 m的扫描导轨上滑动，采用两根导轨可以减小扫描过程中的倾斜。五棱镜的位置由光栅尺测出，光栅尺的测量精度为0.005 mm rms。两个自准直仪安装在导轨的一端，型号均为SH-LTP，由法国Imagine Optic 公司生产，光束口径为27 mm，波长为405 nm，测量精度为100 nrad rms，测量范围为±12 mrad。上述部件都安装在旋转臂上，旋转臂连接于转台上，通过旋转来实现多条径向直线的扫描。转台可以输出旋转臂的角度位置，转台的转角精度为75 μrad rms。当旋转臂旋转时，它的倾斜变化量为70 μrad rms。转台可以在两根水平导轨上滑动，以实现与被测平面镜的对准。该检测系统可以检测口径不大于2.1 m的平面镜的面形。

采用Geckeler介绍的方法[18]对检测系统进行初始调整，初始调整是以自准直仪1为基准的。通过初始调整，可以使所有光学元件的初始倾斜误差均在10 μrad rms以内。

4 误差分析

4.1 倾斜误差

设P1和P2为两个作差的配对点，Δ表示参数从P1到P2的变化量。注意，这里的Δ与2.4节中的Δ的含义不同。利用误差传递公式[19]，通过求偏导数，由式(10)可以得到V从P1到P2的变化量ΔV等于：

ΔV=Δαpp(-2αpp+αac+αst)+

Δγpp(-αac+αst)+

Δαac(αpp-γpp-αst)+

Δαst(-αac+αpp+γpp)-

Δβst+Δβac+ΔV0.

(14)

ΔV实际上就等于式(2)中的δ加上一些误差项。由于自准直仪1是不动的，因此Δαac=Δβac=0；V0是常量，因此ΔV0=0；被测平面镜是不动的，因此βst中的整体倾斜部分没有变化，所以(-Δβst)实际上就是表面倾斜角的差值δ，于是δ的误差Eδ等于：

Eδ=Δαpp(-2αpp+αac+αst)+

Δγpp(-αac+αst)+

Δαst(-αac+αpp+γpp) .

(15)

从式(15)可以看出，通过计算表面倾斜角的差值，使V中的所有一阶误差项全部消除，只剩下很小的二阶误差项。表1列出了一些倾斜误差角的值，这些值来源于2.4节和3节，其中变化量

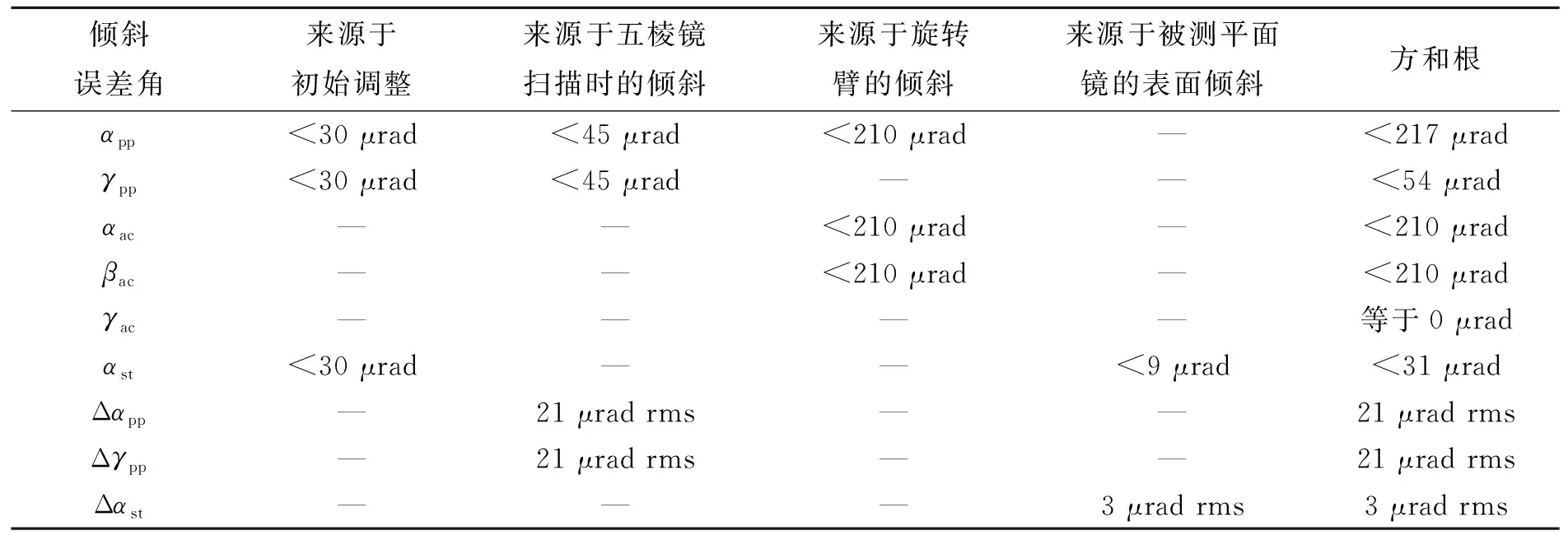
表1 各个倾斜误差角的值Tab.1 Values of tilt angle error

Δαpp，Δγpp和Δαst的值使用rms误差，而其它倾斜误差角的值使用极限误差。在本文中，极限误差等于相应的rms误差的3倍。对于表1，需要注意两点：第一，αac、βac和γac中不含有初始调整误差，因为在初始调整过程中，自准直仪1是基准；第二，γpp和γac中不含有旋转臂的倾斜误差，因为旋转臂的γ倾斜角误差实际上是转台的转角误差，这将在后面的4.3节中进行分析。

表2和表3对Eδ的值进行了计算。注意，在误差分析时，需要将式(15)中的所有负号变为正号；另外，在表3中，将极限误差值看作常数。最后得到由倾斜误差造成的表面倾斜角差值δ的误差Eδ等于11.1 nrad rms。

表2 计算式(15)的一些组成部分Tab.2 Calculations of some components in Equation (15)(μrad)

表3 计算Eδ的值Tab.3 Calculations of Eδ

4.2 自准直仪1的测量误差

自准直仪1的测量误差为100 nrad rms，根据式(2)，可得到相应的表面倾斜角差值δ的误差为：

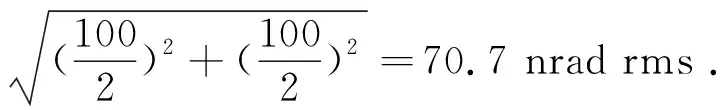
(16)

4.3 测量点的位置误差

转台的转角误差为75 μrad rms，如果被测平面镜的半径为750 mm，则相应测量点的最大位置误差等于：

75×10-6×750=0.056 mm rms .

(17)

光栅尺的测量误差为0.005 mm rms，由此带来的测量点的位置误差也为0.005 mm rms。

在式(10)和式(11)中，除了αst和βst以外的一阶项αpp、γpp、βac、γac、V0和H0，均会使射向被测平面镜的光束产生倾斜，倾斜角的大小分别等于αpp、γpp、βac、γac、V0和H0本身的大小。这种光束的倾斜会带来测量点的位置误差，如表4所示，最后计算得到相应测量点的位置误差为0.052 mm rms。表4中αpp、γpp、βac和γac的值来源于表1，V0和H0的值通过实验标定。

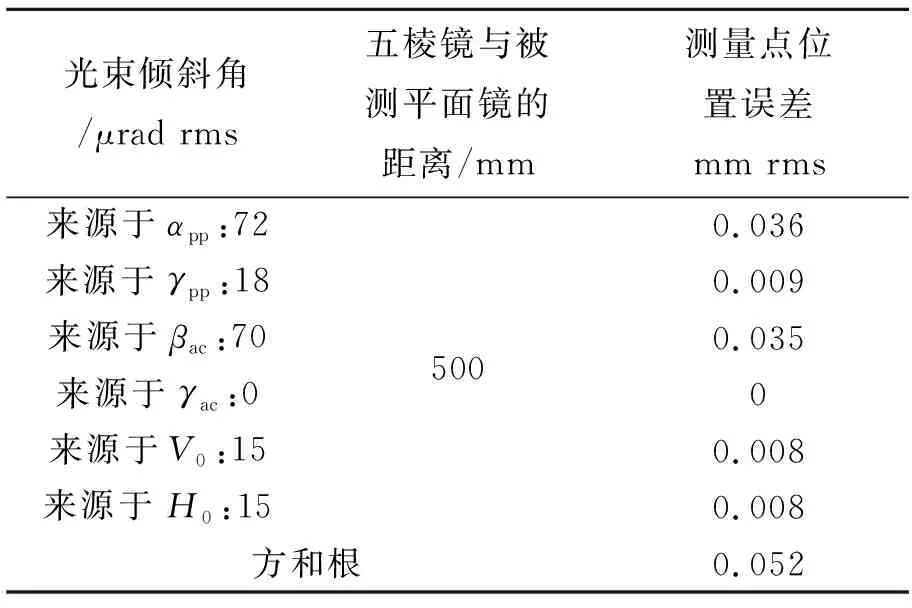
表4 计算光束倾斜带来的测量点位置误差Tab.4 Calculations of the position errors caused by beam tilts

将以上3种来源的测量点位置误差进行合成，得到测量点的总位置误差：

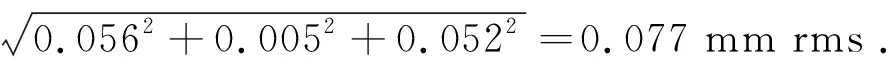
(18)

被测平面镜的表面起伏一般是很平缓的，其表面倾角的变化一般不大于15 nrad/mm。0.077 mm rms的位置误差对应的表面倾斜角的误差等于1.2 nrad rms，于是根据式(2)，相应的表面倾斜角差值δ的误差等于1.7 nrad rms。

4.4 五棱镜的制造误差

五棱镜的制造误差会使出射光产生固定的偏角V0和H0[18]，在4.1节、4.3节中已经对V0和H0进行了分析。 由式(15)可知，V0在作差的过程中已抵消。

4.5 环境变化带来的误差

为了减小环境变化的影响，整个检测系统和被测平面镜放置在同一个隔振平台上，环境温度控制为(20±0.2) ℃。在检测过程中，停止人员的走动和其它无关仪器的工作，以尽量减少振动和空气扰动。

如2.2节所述，五棱镜在两个配对点之间的运动时间为7.5 s，再加上五棱镜倾斜变化量的监视与调整所需的时间，测量两个配对点的时间间隔在10 s左右，在这段很短的时间内，环境的变化量很小，因此环境的影响在作差时几乎可忽略。

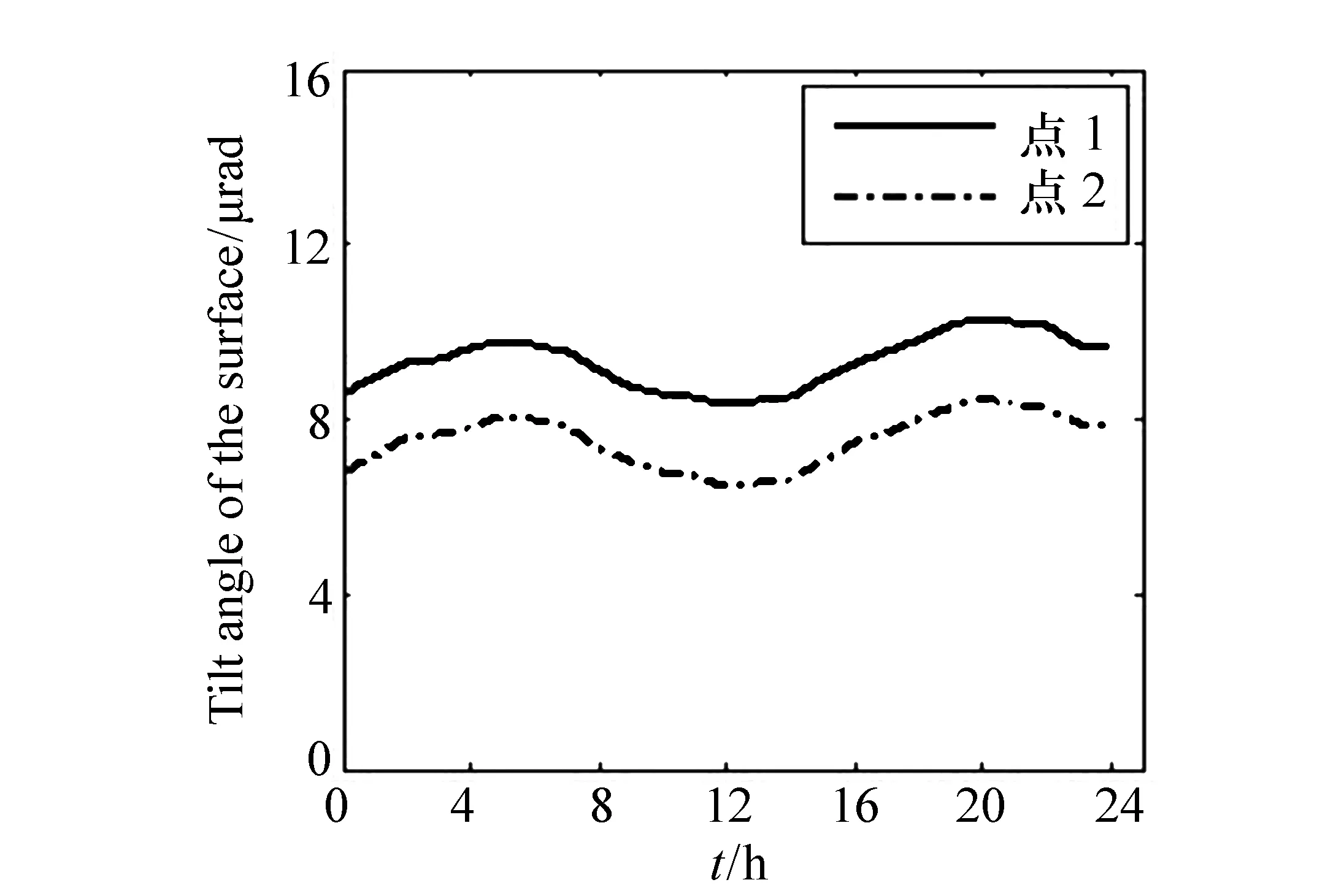
图9 表面倾角的测量结果 Fig.9 Results of the tilt angles of surface

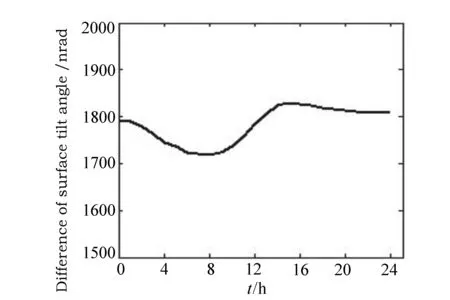
图10 表面倾角差值的测量结果 Fig.10 Results of the surface tilt angle difference

下面通过实验来测量环境变化的误差。在被测平面镜上选择了相距150 mm的两个配对点，分别记为点1和点2，对这两个点的表面倾斜角的差值进行测量，每10 min测量一次，共测量24 h。表面倾角的测量结果如图9所示，表面倾角差值的测量结果如图10所示。从图9可以看出，这两个点的表面倾角的变化趋势是一样的，变化量也几乎相同，因此变化量在作差时可以抵消；从图10可以看出，表面倾角差值的变化量很小。最后计算得到，点1的表面倾角的标准偏差为607.6 nrad，点2的表面倾角的标准偏差为620.2 nrad，表面倾角差值的标准偏差为38.5 nrad。

4.6 表面倾角差值δ的误差汇总

综上，表面倾角差值δ的误差汇总见表5，其总误差为81.3 nrad rms。

表5 表面倾角差值的误差汇总Tab.5 The combined error of the surface tilt angle difference

4.7 仿真分析确定面形检测精度

通过前面的分析得到，表面倾角差值δ的测量误差为81.3 nrad rms，在此基础上，通过仿真分析确定由δ的误差造成的面形检测误差。

按照2.2节中所述的参数进行仿真分析，计算软件采用MATLAB。仿真分析步骤为：第一步，已知对于抛光后的平面镜，其上任意两点的表面倾角的差值大致为3 μrad rms左右，其随机产生440个3 μrad rms的表面倾角差值，分别与440对配对点相对应，然后利用这些表面倾角差值，按2.3节的方法计算出面形，记为面形1；第二步，随机产生440个81.3 nrad rms的误差值，把这些误差值分别加到440个表面倾角差值上，得到含有误差的440个表面倾角差值，再利用它们来计算出含有误差的面形，记为面形2；第三步，将面形2与面形1作差，得到面形检测误差，再计算该面形检测误差的rms值。

按以上步骤重复计算10次，得到10个rms值，它们的最大值为7.2 nm rms，即为由δ的误差造成的面形检测误差。

在2.5节中，已经通过仿真分析得到了检测的原理误差，为2.3 nm rms，于是总的面形检测误差等于：

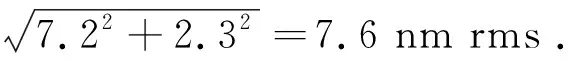
(19)

所以五棱镜扫描法的面形检测精度为7.6 nm rms。

5 检测实验与结果对比

采用图8所示的检测系统对一块口径为1.5 m的平面镜的面形进行了检测实验，如图11所示，检测原理与检测参数如第2节所述。

图11 检测1.5 m口径平面镜的面形 Fig.11 Surface shape detection of a 1.5 m flat mirror

对面形共检测了5次，5次检测的平均面形如图12所示。5次检测的标准偏差如图13所示，最大标准偏差为6.1 nm，仅出现在平面镜边缘，平均标准偏差为4.0 nm，可见，检测重复性较好。

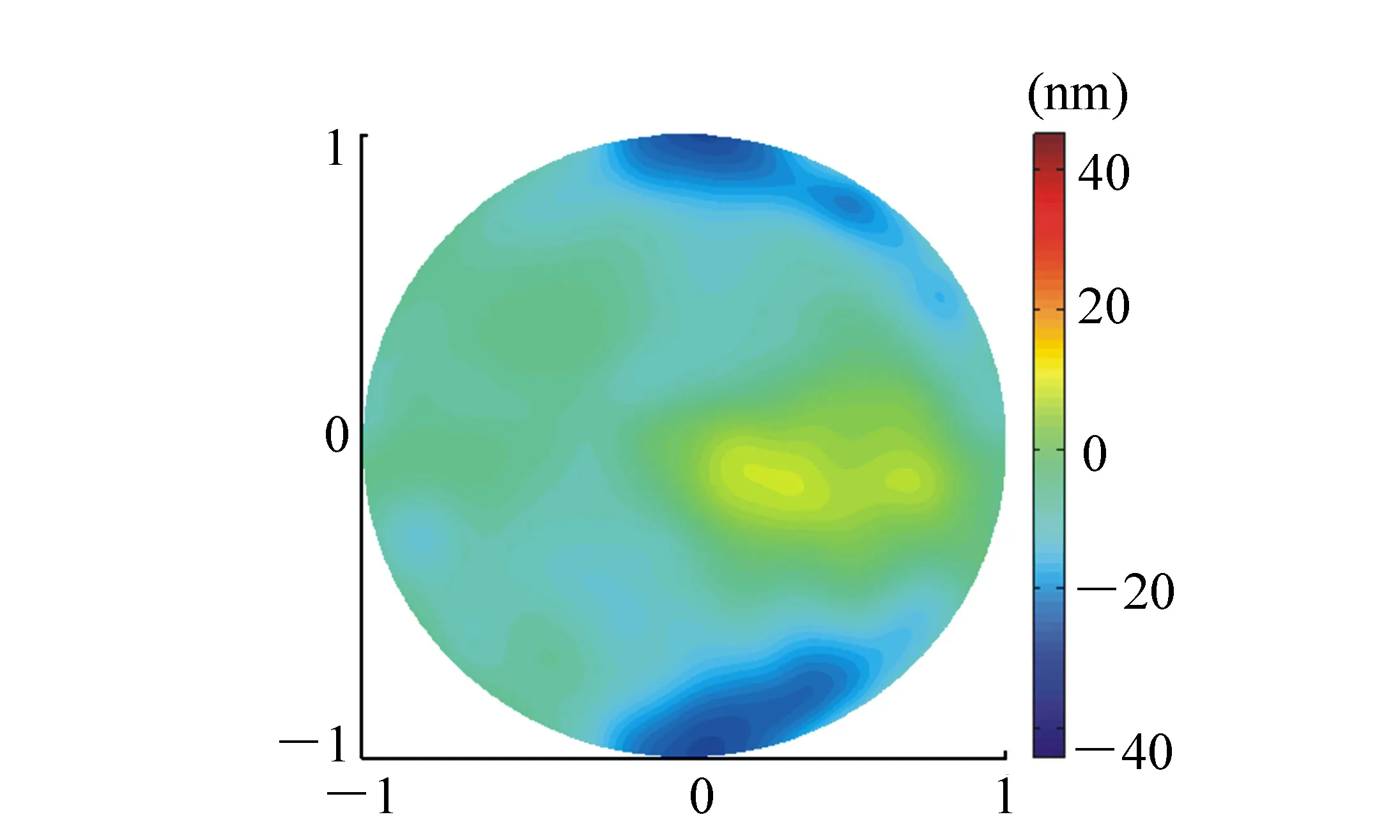
图12 5次检测的平均面形(PV=45.3 nm，RMS=13.2 nm) Fig.12 Average surface shape of 5 times of measurements(PV=45.3 nm，RMS=13.2 nm)

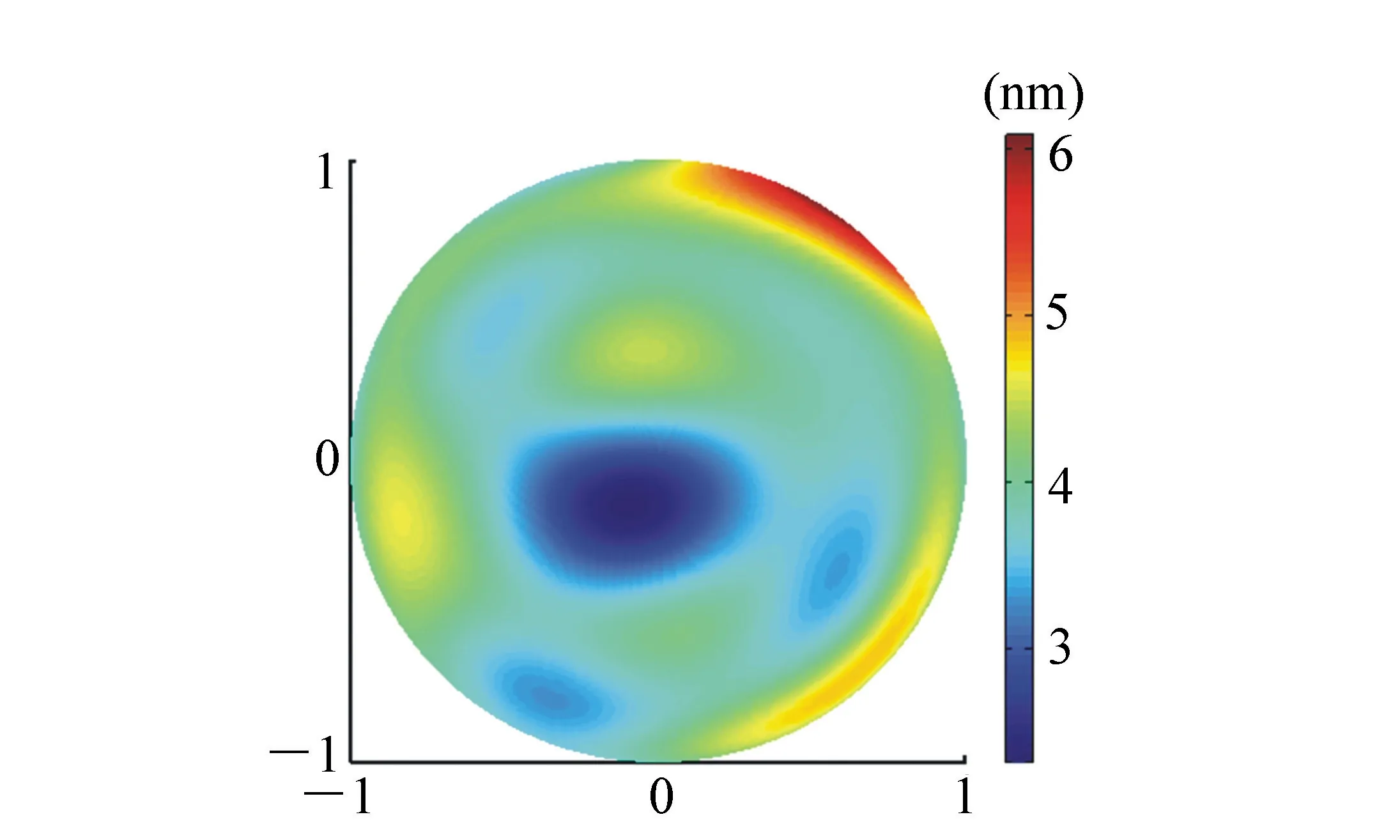
图13 5次检测的标准偏差 Fig.13 Standard deviation of 5 times of measurements

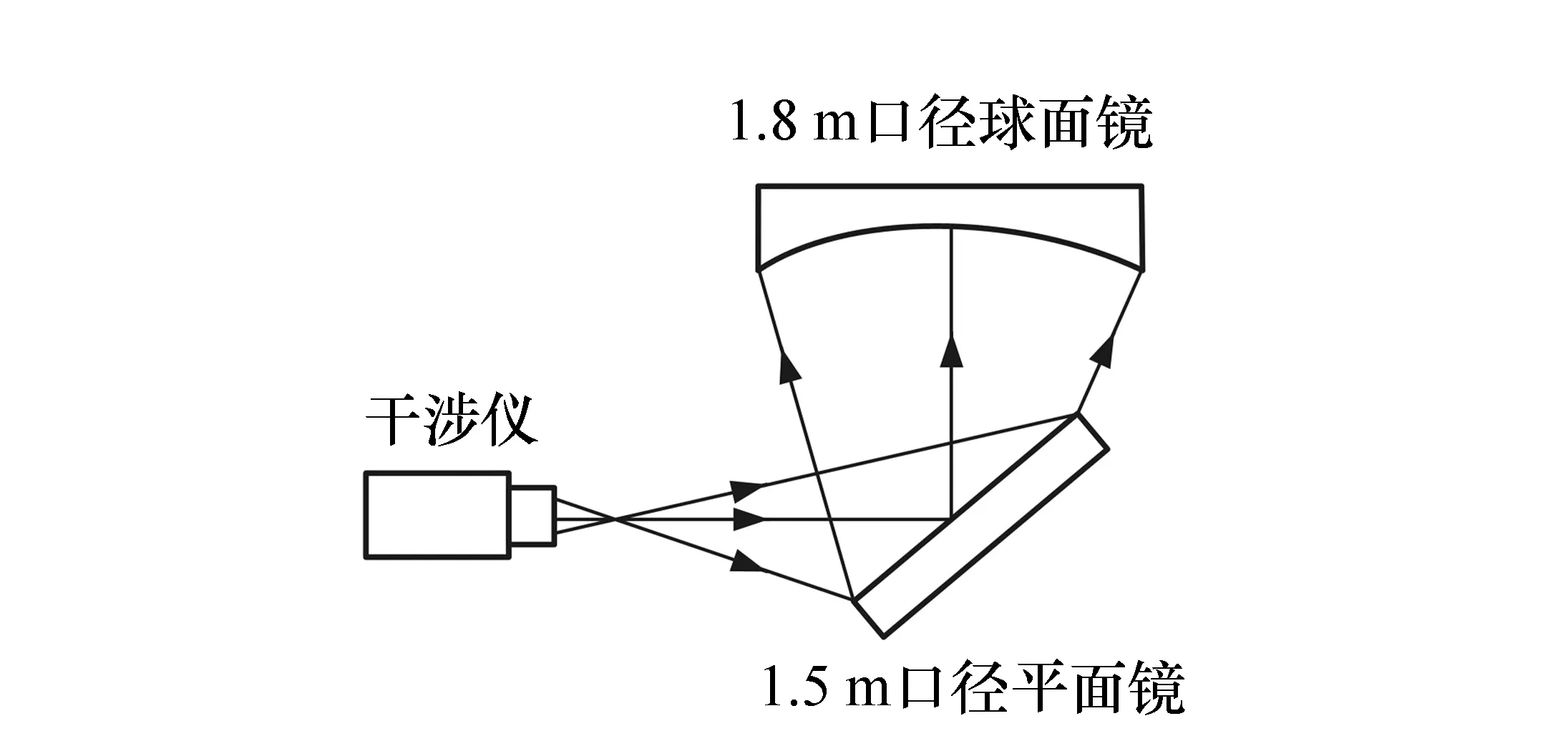
图14 Ritchey-Common法的检测光路 Fig.14 Light path of Ritchey-Common method

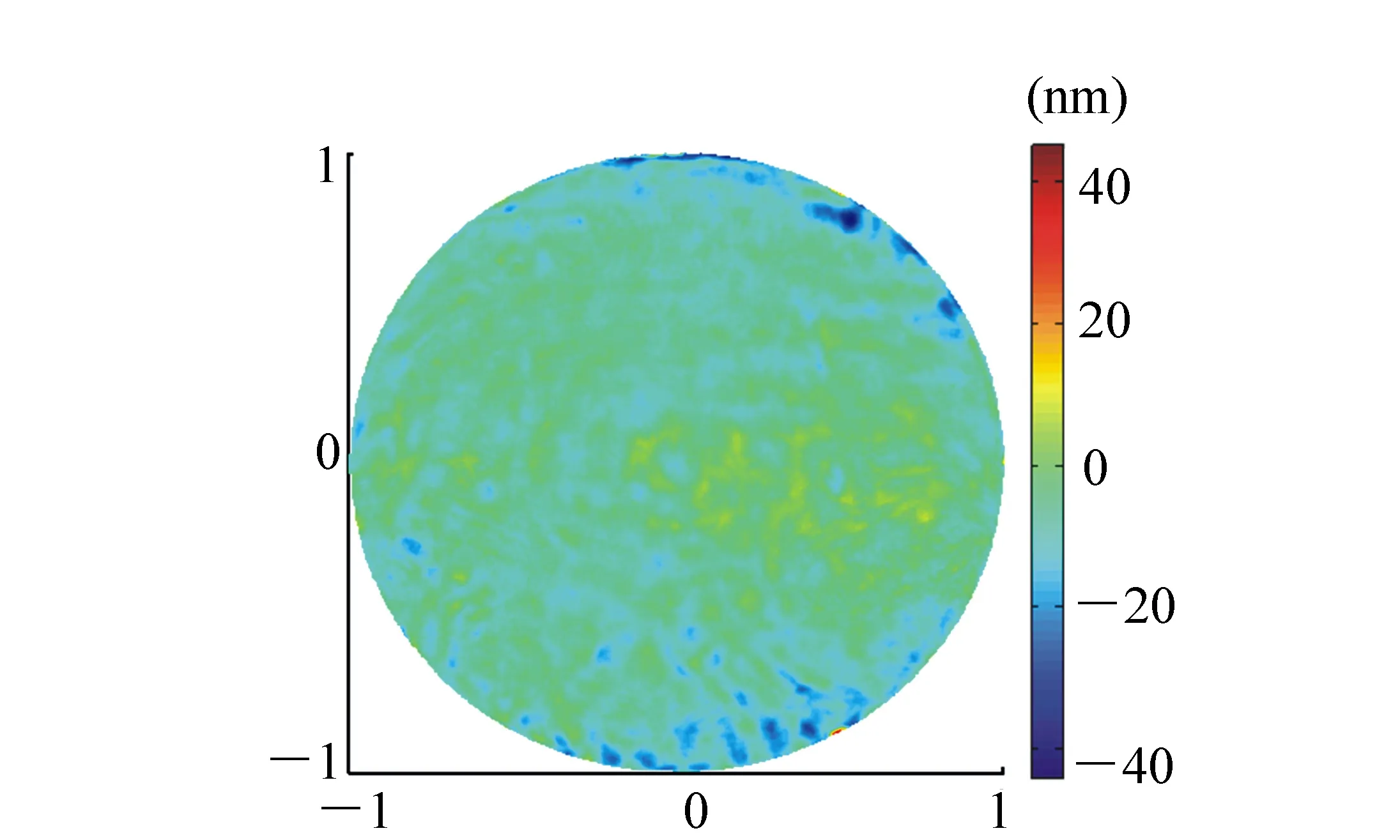
图15 Ritchey-Common法检测得到的平面镜面形(PV=79.1 nm，RMS=11.5 nm) Fig.15 Flat mirror surface shape detected by Ritchey-Common method(PV=79.1 nm，RMS=11.5 nm)

朱硕用Ritchey-Common法对同一块平面镜的面形进行检测[17]，检测光路如图14所示，检测得到的平面镜面形如图15所示。将图12与图15比较后可知，从整体上来看，两种方法得到的面形的分布比较相似：在中部偏右的值都比较大，在右上边缘和右下边缘处的值都比较小，在其它位置处的值都居中。两者的RMS值差距也不大，但是PV值差距较大，下面进行详细分析。

Ritchey-Common法使用的干涉仪的CCD分辨率为1 024 pixel×1 024 pixels，换算到被测平面镜上，采样间距和采样口径均为1.5 mm左右，而本文的五棱镜扫描法的平均采样间距达到了60 mm，采样口径达到了27 mm，所以，五棱镜扫描法的检测频率要远低于Ritchey-Common法。因此，在图15中，Ritchey-Common法得到的面形的高频信息较多，面形分布比较散乱；而在图12中，五棱镜扫描法得到的面形的高频信息较少，面形分布比较平滑。注意，在图15的右下边缘处有一块很小的红色区域(彩图见期刊电子版)，表示此处有一个面积很小的突起，Ritchey-Common法检测到了这个突起，它对PV值的贡献达到了30 nm左右，而五棱镜扫描法由于检测频率较低，所以没有检测到这个突起，从而大大减小了PV值，可见，这个突起是两者的PV值差距较大的主要原因。

将Ritchey-Common法的面形结果作低通滤波后得到如图16所示的面形，滤波器采用巴特沃斯低通滤波器[20-21]。五棱镜扫描法的平均采样间距为60 mm，所以根据采样定理，低通滤波的截止频率等于：

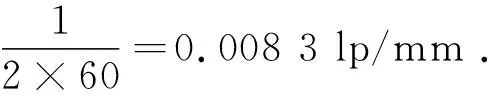
(20)

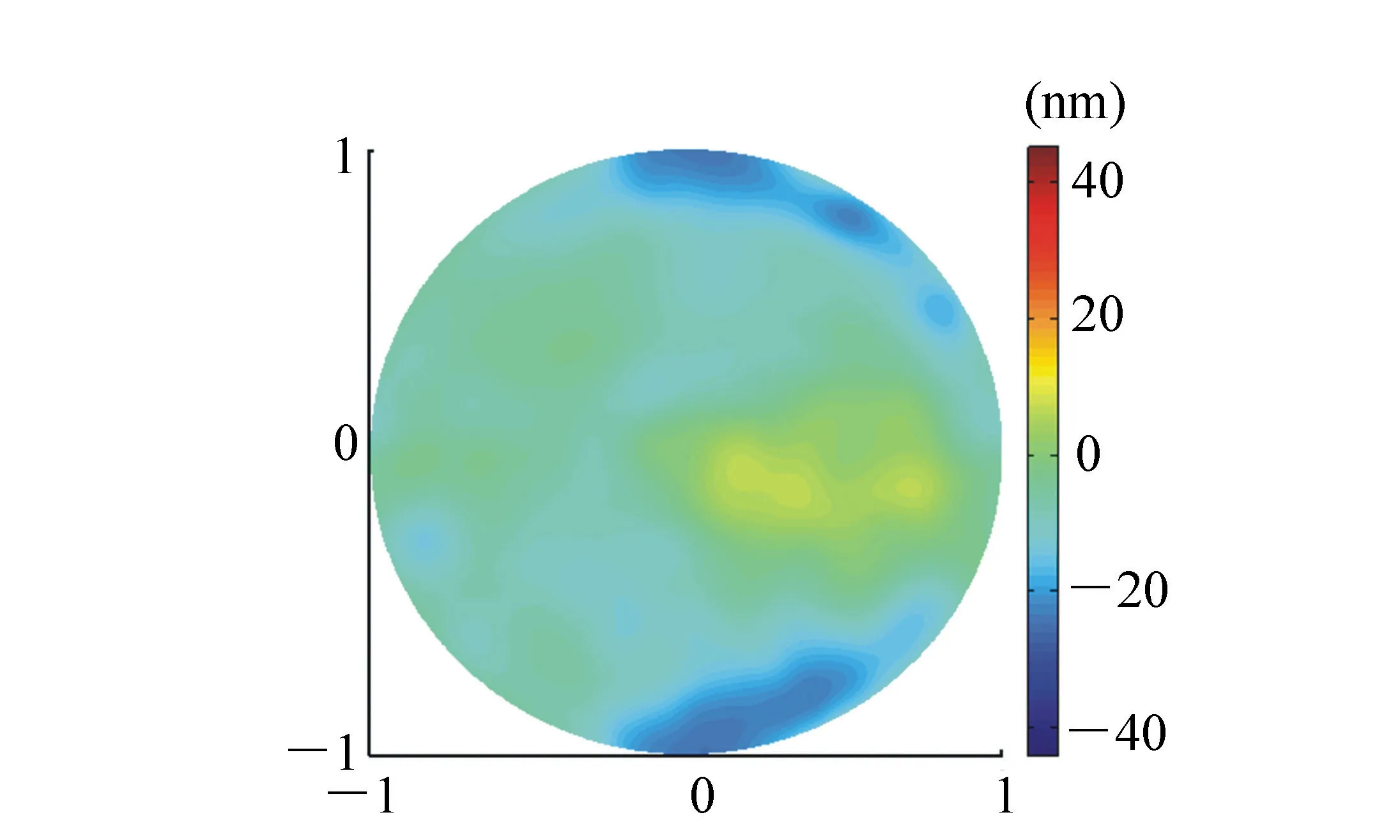
图16 将图15作低通滤波后的面形图 (PV=43.8 nm，RMS=11.9 nm) Fig.16 Surface shape of Fig.15 after low pass filtering (PV=43.8 nm，RMS=11.9 nm)

将图16与图15比较后可知，经过低通滤波后，面形变得平滑，由于右下边缘的突起被滤掉了，所以PV值下降较多，但RMS值变化不大。将图16与图12比较可知，与滤波前相比，两者的面形分布更加相似，都较平滑，PV值也更加接近了。可见，五棱镜扫描法的面形结果相当于是Ritchey-Common法面形结果的低频部分。

实际上，五棱镜扫描法的检测频率是可控的，通过减小采样间距和采样口径，增加Zernike多项式的项数，就可以提高检测频率；反之，通过增大采样间距和采样口径，减少Zernike多项式的项数，就可以降低检测频率。下一步，本项目组计划提高五棱镜扫描法的检测频率再进行实验。

另外，在检测过程中，检测频率、采样间距、采样口径以及Zernike多项式的项数这4个参数要相互匹配，这样才能检测出该频率下正确的面形。匹配的原则是：如果需要的检测频率较高，则采样间距和采样口径就需要小一些，Zernike多项式的项数就需要多一些；如果需要的检测频率较低，则采样间距和采样口径就需要大一些，Zernike多项式的项数就需要少一些。本文根据上述匹配原则，确定了平均最高检测频率为0.008 3 lp/mm，平均采样间距为60 mm，采样口径为27 mm，Zernike多项式的项数为36。通过前面所述的仿真分析和检测实验已证明这4个参数是相互匹配的。

最后计算得到，图12与图15的差值rms值为7.1 nm，图12与图16差值的rms值为3.2 nm，均小于五棱镜扫描法的面形检测精度7.6 nm rms，可见本文检测方法是正确的。

6 结 论

本文提出了一种新的五棱镜扫描法检测大口径平面镜的面形。该方法使用一个扫描的五棱镜和一个自准直仪测量表面倾斜角的差值，然后建立方程组，最后采用最小二乘法计算得到被测平面镜的面形。

该方法可以有效减小各种测量误差：第一，五棱镜本身的误差抑制特性以及表面倾斜角差值的计算可以消除倾斜误差的一阶影响；第二，五棱镜倾斜变化量的监视与调整可以减小倾斜误差的二阶影响；第三，仅使用一个五棱镜以及表面倾斜角差值的计算可以消除五棱镜制造误差的影响；第四， 通过计算表面倾斜角差值、严格控制环境以及保证两个配对点的测量时间间隔较短，可以减小环境带来的误差；第五，两个配对点之间较长的距离可以减小相对误差。

误差分析表明，该方法的面形检测精度为7.6 nm rms。采用该方法对一块1.5 m口径的平面镜的面形进行了检测，并与Ritchey-Common法的检测结果进行了对比，两种方法的面形结果的差异为7.1 nm rms，小于该五棱镜扫描法的面形检测精度，证明了利用该五棱镜扫描法检测大口径平面镜面形的正确性。