真值为格值的二型模糊集及其运算
2019-08-31严卫平王学平
严卫平, 王学平
(四川师范大学 数学与软件科学学院,四川 成都610066)
二型模糊集的概念是由Zadeh[1]在1975年首次提出,他扩展了一般模糊集和区间值模糊集的概念.文献[2-4]给出了二型模糊集的性质与运算.2001年,Karnik等[5]讨论了二型模糊集的集合运算(包括取小与乘积t-模的并交运算)、代数运算、二型模糊集隶属度的性质、二型模糊关系及其合成.2002年,Mendel等[6]介绍了二型模糊集的表示定理,他们不使用扩展原理而用表示定理证明了并、交、补运算.2005年,Walker等[7]等讨论了二型模糊集的真值运算与真值代数,并对二型模糊集真值代数的结构进行了研究.2007年,Hading等[8-9]研究了二型模糊集真值代数的子代数,证明了它的一些子代数是格,且讨论了格的完备性.2010年,Harding等[10]还讨论了二型模糊集真值代数的生成问题.2014年,Walker等[11]给出了有限链上二型模糊集的运算性质.2014年,Hu等[12-13]在文献[7]的基础上讨论了线性序集上二型模糊集真值的二元运算的扩展t-模运算,随后又讨论了二型模糊集的t-模运算、二型模糊数的性质、二型模糊关系以及区间值二型模糊集.2014年,Wang等[14]在文献[12-13]的基础上讨论了蕴含运算.2016年,Gonzalo等[15]给出了次隶属函数的广义二型模糊集的交与并运算等.
以上讨论都是在[0,1]上.本文是在文献[7,12]的基础上,将[0,1]拓展到完备分配格上,讨论真值为格值的二型模糊集的运算及其性质.
1 完备分配格L上的二型模糊集的模糊真值运算
设L是完备分配格(有关格知识参见文献[16]),X 上的模糊集是映射A:X→L,称A(x)为模糊集A在x处的隶属度,称X为模糊集A的定义域,称L为模糊集A的值域.所有X到L的映射构成的集合记为Map(X,L).对任意A,B∈Map(X,L),定义A≤B当且仅当对任意x∈X,A(x)≤B(x).对任意Ai∈Map(X,L),x∈X,定义(∪Ai)(x)=∨Ai(x), (∩Ai)(x)=∧Ai(x),i∈Ii∈Ii∈Ii∈I其中I为指标集.易见,模糊集的序≤,运算∪及∩均以点式定义方式来源于格(L,≤,∨,∧).设J为完备分配格L的完备子格.拓展二型模糊集的定义如下.
定义1.1 设X为非空集合,称映射A:X→Map(J,L)为X上二型模糊集.
记X上所有二型模糊子集构成的集合为Map(X,Map(J,L)).Map(J,L)的元素是L 的一般模糊集.与Map(X,L)一样,Map(X,Map(J,L))中二型模糊集的运算可从Map(J,L)的运算以点式定义方式得到.与文献[7]中Map(X,Map(J,[0,1])的二型模糊集的运算一样,可以使用卷积构造Map(J,L)上的运算.设U、V 是2个集合,ο是U 上的二元运算,▲是V上的二元运算,▼是V上另一二元运算,则可用如下方式定义集合Map(U,V)上的二元运算·:对任意f,g∈Map(U,V),定义称f·g为f与g的卷积.

以下利用卷积运算,可以定义Map(J,L)上的运算.
定义1.2 如果映射N:L→L满足:
1)对任意x,y∈L,如果x≤y,则N(y)≤N(x);
2)对任意x∈L,N(N(x))=x,则称N为L上的强否定.
定义1.3 设f,g∈Map(J,L),N 为L 上强否定运算,定义fg和fg如下:

定义1.4 设f∈M,定义M中的fL和fR如下:对任意x∈J,

易见,函数fL是单调递增的,而fR是单调递减的.
定理1.1 设f,g∈M,则:
1)f≤fL,f≤fR;
2)(fL)L=fL,(fR)R=fR;
3)(fL)R=(fR)L,因此(fL)R可以写成fRL或者fLR;

证明 由定义1.4知1)、2)与8)显然成立.
3)对任意x∈J,

因此,任意x∈L,

4)对任意x∈J,

又

5)对任意x∈J,

即(f∪g)L=fL∪gL.类似可证(f∪g)R=fR∪gR.

6)对任意x∈J,所以(f∩g)L≤fL∩gL.类似可证

7)对任意x∈J,

定理1.2 设f,g∈M,则:

证明 对任意x∈J,f,g∈M,

又由(L,∨,∧,0,1)是完备分配格知(Map(J,L),∩,∪,0-,1-)是完备分配格,因此

(由定理 的结论 ))1.11

所以

类似有


所以

注1.1易见,如果定理1.2中函数f与g均是单调递增的,则等号成立 因为此时.

但等号一般不成立.
例1.1 设L={0,a,b,1}满足a与b不可比,且a∨b=1,a∧b=0,则易见(L,∧,∨,0,1)是完备分配格.
1)设f(0)=1,f(a)=a,f(b)=b,f(1)=0;g(0)=1,g(a)=b,g(b)=a,g(1)=0,则

而

所以
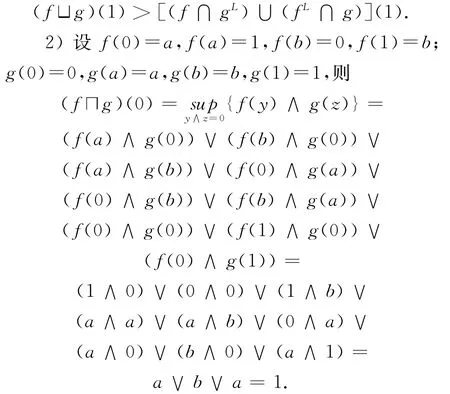
而

所以

命题1.1 设f,g∈M,则:
2)fLgL≥fL∩gL,fL∩gL≤fLg;
3)fRgR≥fR∩gR,fR∩gR≤fRg;

证明 1)对任意x∈J,

2)由定理1.2及定理1.1的结论2)知

3)由定理1.2及定理1.1的结论2)知

4)对任意x∈J,

5)由定理1.2直接可证.
命题1.2 设f,g∈M,则:

证明 1)对任意x∈J,



因此,若y∧z≤x,则存在y1,z1∈J使得y1≥y,z1≥z,y1∧z1=x.故

又对任意x∈J,因为

因此,若y∨z≥x,则存在y1,z1∈J使得y1≤y,z1≤z,x=y1∨z1.故

又对任意x∈J,因为


注1.2 命题1.2中等号一般不成立.
例1.2 设格L是平面的所有闭子集构成的完备分配格,且f,g∈Map(L,L).

由命题1.1的结论2)知fLgL≥fL∩gL,所以(fg)L(x)<(fLgL)(x),即(fg)L<fLgL.同理可证其余等式也不成立.

注1.3 定理1.3中等号一般不成立.
例1.3 设L={0,a,b,1}满足a与b不可比,且a∨b=1,a∧b=0,则易见(L,∧,∨,0,1)是完备分配格.
1)设f(0)=a,f(a)=b,f(b)=1,f(1)=0,
则


所以

2)设f(0)=0,f(a)=a,f(b)=1,f(1)=b,则:

定理1.4 设f,g,h∈M,则:
证明 1)对任意x∈J,

2)对任意x∈J,因此,


定理1.5 设f,g,h∈M.若格L是无限分配的,则:

证明 对任意 , x∈J

(由L的无限分配性)

(由L的无限分配性)

定理1.6 设f,g,h∈M,则:

证明 对任意x∈J,

定理1.7 设f,g,h∈M.若格L是无限分配的,则:

证明 对任意x∈J,(由L的无限分配性)


注1.5 定理1.7中等号一般不成立.
例 设 ( (), ), {,,},1.4 L=PowA∈A=012设f,g,h∈Map(L,L),

设x=1L,则


