网络编码错误空间与信息空间交空间的维数

刘海波， 廖群英

（四川师范大学 数学与软件科学学院，四川 成都610066）

1 预备知识

网络编码（Network Coding）是由 Yeung等［1］提出，随后由Ahlswede等［2］进一步发展起来．因为网络编码能显著地提高信息的传输效率，所以一直是近年来的研究热点，尤其对无错误发生的网络，可参见文献［3－10］．遗憾的是在实际网络传输中会出现许多种类的错误．为应对这种问题，学者们提出了网络纠错编码（Network Error Correction Coding），参见文献［11－13］．事实上，网络纠错码可以看作经典纠错码的推广，即在经典纠错码里的某些界都可以推广到网络纠错码中，例如Singleton界、Hamming界和 Gilbert－Varshamov界［11－12］．达到Singleton界的线性网络纠错码称为线性网络极大距离可分码，简称为网络MDS码．作为一类好的网络纠错码，网络MDS码无论在理论研究还是在现实应用中都有着重要的地位，参见文献［14］．

在实际的网络通讯中，需要信源通过不同的信息率传递不同的信息．在这种情况下，考虑到纠错的情形，Guang等［15］构造一类变率的网络 MDS码，这其中涉及到对网络MDS码信息空间与达到最小距离的错误空间的交空间的维数刻化．本文将进一步刻化一般网络纠错码的信息空间与达到最小距离错误空间的交空间的维数；在给定错误模式的前提下，给出网络MDS码信息空间与该错误模式所生成的错误空间的交空间的维数的界．

接下来介绍相关的概念与记号．通讯网络是定义在有限非循环的有向图G＝（V，E）上的，其中V表示点集，E表示边集．点集V由不相交的3部分S、T以及J构成，其中S是信源节点集，T是信宿节点集，J＝V＼（S∪T）是中间节点集．

有向边e＝（i，j）∈E表示由节点i到节点j，节点i与j称为边e的尾与头，记作i＝tail（e），j＝head（e）．边e称为i输出信道，j的输入信道．给定节点i，记Out（i）为i的输出信道集，In（i）为i的输入信道集．

本文中考虑的是｜S｜＝1的情形，即有唯一的信源节点s．显然信源节点s没有输入信道，信宿节点没有输出信道，为叙述方便，对信源节点s引入虚拟输入信道．假设s单位时间内传输ω个域F上的元素X＝［X1X2…Xω］，则信源节点s有ω个虚拟输入信道d′1，d′2，…，d′ω，即

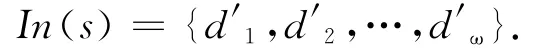
令Ue为信道e上传递的ω－维的向量，则在信源节点s，有Ud′i＝Xi（1≤i≤ω）．在节点i∈V＼T，称｜In（i）｜×｜Out（i）｜矩 阵 Ki＝ ［kd，e］d∈In（i），e∈Out（i）为节点i的局部编码矩阵，其中kd，e∈F为相邻信道（d，e）局部编码系数．对于e∈E上传递的信息Ue，可以由如下的式子迭代得到易见Ue是ω个向量Xi（1≤i≤ω）的线性组合．若存在F上ω维的列向量fe，满足Ue＝X·fe，则称fe为信道e的全局编码系数［6－7］，即

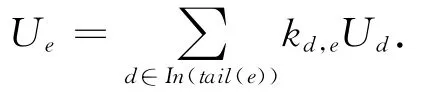
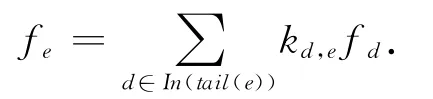
当有错误发生在信道e上时，记错误为Ze∈F，则信道e的输出为珦Ue＝Ue＋Ze．特别地，将Ze视作信息称为错误信息，定义｜E｜－维的错误向量为Z＝［Ze：e∈E］．对于信道e∈E，存在虚拟信道e′与e的尾相连，提供错误信息Ze．为了区分虚拟信道，称d′i（1≤i≤ω）为虚拟信息信道，e′∈E′为虚拟错误信道．称珟G＝（珟V，珟E）为G扩展网络，其中珟V＝V，珟E＝E∪E′∪｛d′1，d′2，…，d′ω｝，E′＝｛e′：e∈E｝．令ke′，e＝1，对于d∈E／｛e｝，kd，e＝0，则G 上线性网络编码可以扩展到珟G上．类似地，对于e∈珟E，可以定义扩展的全局编码系数珟fe，以及线性的网络纠错码．

定义1．1［15］F上ω－维的线性网络纠错码是由满足如下条件的扩展的全局编码系数构成：

1）当1≤i≤ω时，珟fd′i＝1d′i；当e′∈E′时，珟fe′＝1e，其中1d（d∈In（s）∪E）为（ω＋｜E｜）－维的列向量的指标函数．

2）对于其他e∈E，

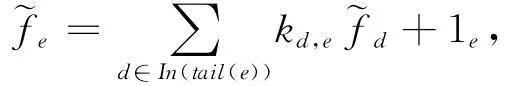
其中kd，e∈F为相邻信道（d，e）的局部编码系数．

在信宿节点t∈T，令rowt（d）为解码矩阵

中被指标d∈In（s）∪E所确

定｜In（t）｜－维的行向量．错误模式ρ为某些信道的集合，即ρE，称错误信息Z＝［Ze：e∈E］匹配错误模式ρ是指对于e∈E／ρ，Ze＝0．对于错误模式ρ，以及t∈T，定义错误空间Δ（t，ρ）＝｛（0Z）珟Ft＝Z·Gt：Z∈ F｜E｜匹配ρ｝，以及信息空间 Φ（t）＝｛（X0）＝X·Ft：X∈Fω｝．记其中，L表示向量的集合，〈L〉由L中所有向量生成的子空间．

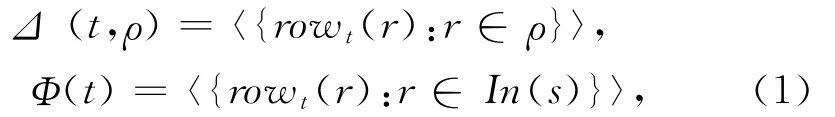
定义1．2［14］对于线性网络纠错码，在信宿节点t∈T的最小距离定义为其中｜ρ｜记为错误ρ的阶．

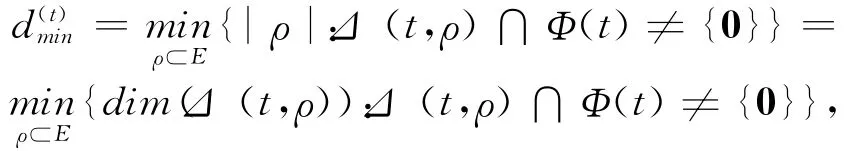
引理1．3［14］（Singleton界） 令d（t）min为线性网络纠错码在信宿节点t∈T的最小距离，则其中，Ct为信源节点s与信宿节点t的最小割，ω为信息率，δt＝Ct－ω为信宿节点t的冗余．

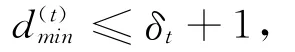
达到这个界的网络纠错码称为网络MDS码．对于网络MDS码与达到最小距离错误空间的交空间的维数，Guang等［15］给出了如下刻化：

引理1．4［15］设Cω为G 上ω－维的网络 MDS码，则对于任意的信宿节点t以及错误模式ρ∈Q（t）有

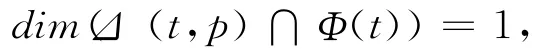
2 主要结果及证明

本节给出本文的主要结果及证明，即定理2．1和2．2．定理2．1将文献［15］中结果推广到一般的网络纠错码．在给定错误模式的前提下，定理2．2给出其错误空间与网络MDS码信息空间的交空间维数的界．

定理2．1 设Cω为G上ω－维网络纠错码，则对于任意的信宿节点t∈T以及错误模式ρ∈Q（t）有

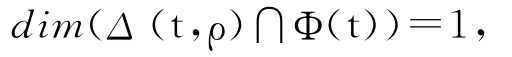
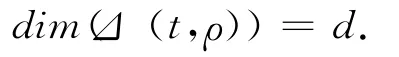
令r1，r2，…，rd为Δ （t，ρ）中d 个线性无关向量，即．假设dimΔ（ （t，ρ）∩Φ（t））≥2，令珒l1、珒l2为交空间Δ（t，ρ）∩Φ（t）中的2个线性无关的向量，则在F存在两组不全为0的数组a1，a2，…，ad与b1，b2，…，bd满足对于i＝1，2，…，d，ai或者bi中一定有一个为0，否则，若存在某个i（1≤i≤d）满足ai≠0，bi≠0，即有

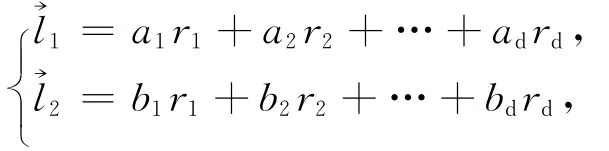
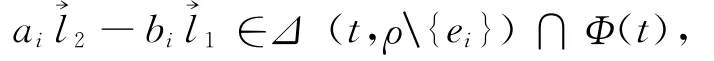
且ail2－bil1≠0．故

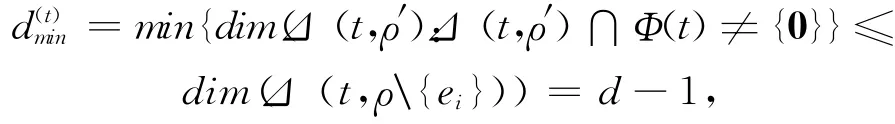
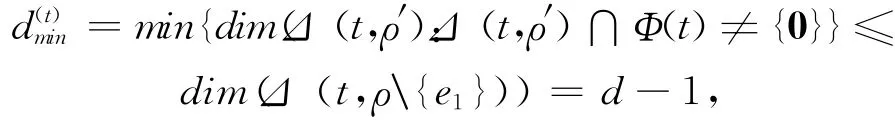
这也与d（t）min＝d矛盾．

综上，对于任意的ρ∈Q（t），有

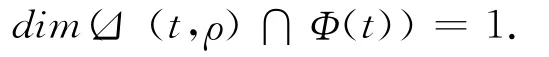
对网络MDS码Cω，在信宿节点t∈T定义错误模式的集合为

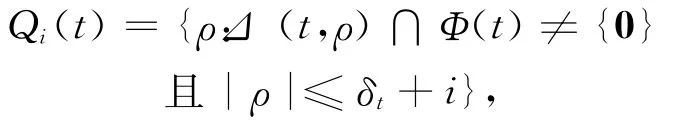
其中1≤i≤｜E｜－δt．对于任意的信宿节点t∈T以及错误模式ρ∈Qi（t），如下的定理2．2给出的界．

定理2．2 设Cω为G上ω－维网络MDS码，则对任意的信宿节点t∈T以及错误模式ρ∈Qi（t），有

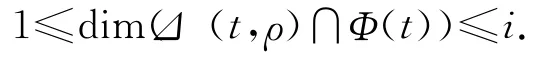
证明 对i用数学归纳法．当i＝1时，由引理1．4即得．假设当i＝k－1（k＞1）时，结论成立．

当i＝k 时，注意到 Qk（t）＝Qk－1（t）∪ ｛ρ：则只需证明对于任意信宿节点t∈T，以及错误模式ρ∈Qk（t）且，满足即可．事实上，对于任意，由（1）式有．另一方面，根据定义1．2，有因此，对于任意的有为叙述方便，记，其中．令为Δ （t，ρ）中d 个线性无关的向量，即

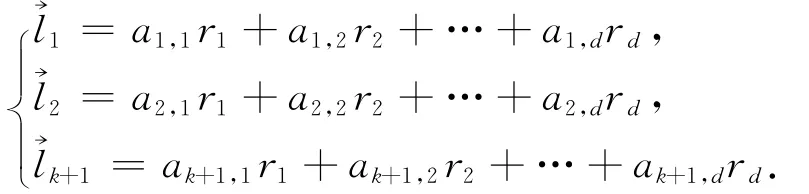
所以，对于1≤j≤k＋1，由于存在某些aj，1＝0，不失一般性，对于1≤c≤d，假设c）且如若不然可以调整d个向量r1，r2，…，rd的顺序．对于1≤j≤c，有珒lj∈，即对于，由有

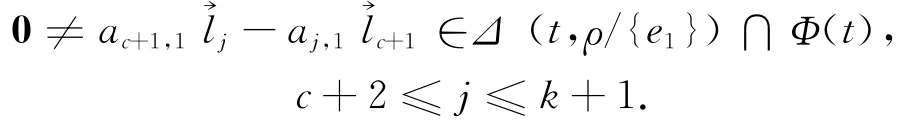
由归纳假设，知k个向量珒lj（j＝1，2，…，c），

中线性相关的，即存在不全为0的b1，…，bk∈F，满足

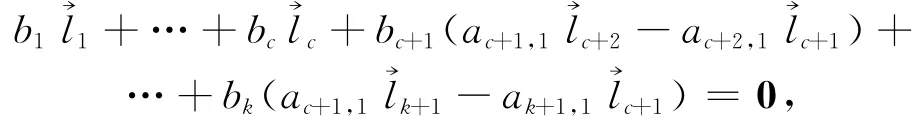
等价于

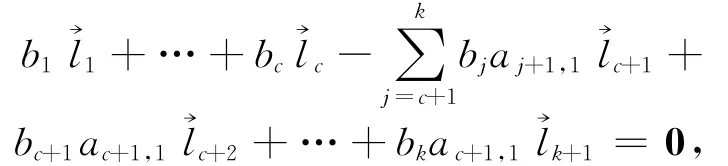
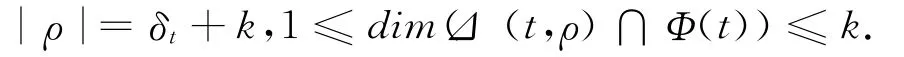
这就证明了定理2．2．