一类具有Beddington－DeAngelis型功能反应的非自治捕食－被捕食系统的渐近行为

沈怡心， 蒲志林， 胡华书

（四川师范大学 数学与软件科学学院，四川 成都610066）

0 引言

研究捕食－被捕食系统的动力性质是生物学家非常关注的问题，捕食－被捕食系统中一个重要的关系就是捕食者依赖于被捕食者的程度，即为捕食者的功能反应，功能反应是严格依赖于捕食者的．常见的功能反应类型有 Holling I－III型［1－3］、Goldstein－ Neill 型［4］、Hassell－ Varley 型［5］、Growley－Martin型［6］、比率相依型［7］及 Beddington－DeAngelis型［4，8］．

具有HollingⅡ型功能反应［2］的 Kolmogorov型的捕食－被捕食系统为其中，x代表被捕食者，y代表捕食者．该系统的不同形式引起了理论和数学生物学家的极大兴趣．但是依赖于捕食者的功能反应，不能体现捕食者自身的影响，并且在生物学和生理学上也面临着挑战．Arditi等［7］在此基础上提出了比率相依捕食－被捕食模型

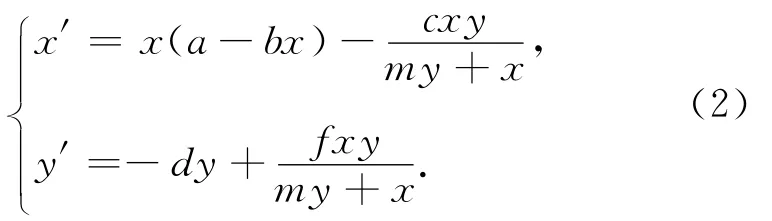
这种模型引入了捕食者的影响，更丰富地体现其中的动力学性质．但当低密度时，该系统部分性质会引起矛盾．Skalski等［2］从19个捕食与被捕食系统中得到统计数据，表明3种功能反应（Beddington－DeAngelis型、Crowley－Martin型和 Hassell－Varley型）能更好地体现捕食者依赖于捕食－被捕食系统中各个量的程度．在某些条件下Beddington－DeAngelis型功能反应能更好地体现这种关系．由 Beddington［8］和 DeAngelis等［4］分别提出的具Beddington－DeAngelis型功能反应的捕食－被捕食系统为

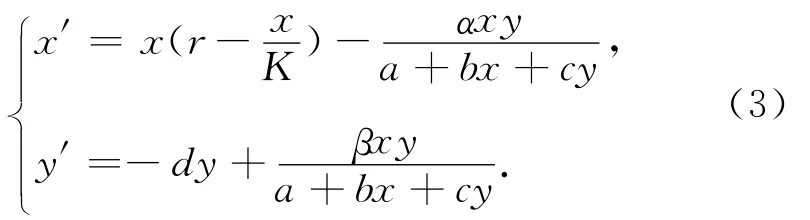
这个模型具有Holling II型功能反应的特点，在分母中增加的项cy体现了捕食者之间的相互影响．该模型又具有比率相依型功能反应的一些性质，并且克服了比率相依型在低密度下的缺陷．这类具有Beddington－DeAngelis型功能反应的模型被广泛研究，其全局动力学行为得到了很好的结果［9－11］．但这些结果都是在常数环境下得到的，这在实际生活中是很少见的，大多数的自然环境都是多变的，出生率、死亡率等其他与种群数量相关的量大都依赖于时间，因此，Meng等［12］研究了具有Beddington－DeAngelis型功能反应的非自治捕食与被捕食系统

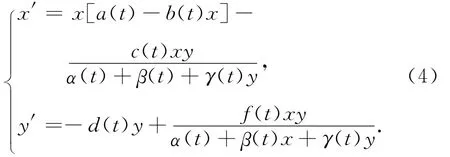
Meng等［12］对非自治系统（4）研究了t→∞时的持久性、解的全局渐近稳定性及周期解的相关性质，该非自治系统的拉回渐近性态仍有待研究．

文献［13］研究了非自治Lotka－Volterra系统的向前和拉回渐近性态．本文主要借鉴文献［13－14］的方法，对具Beddington－DeAngelis型功能反应系统的拉回行为进行研究．

为探索具Beddington－DeAngelis型功能反应的非自治捕食与被捕食系统的拉回行为，本文将系统简化为只有一个系数与时间t相关的方程

其中，a、c、d、α、β、γ都是正的常数，b（t）是 R上的有界连续函数，且恒为正．本文给出了这个方程的向前行为，并利用上下解、比较原理及logistic方程探索其拉回行为．

1 预备知识

首先介绍本文将用到的一些概念和术语等．

定义1．1［14］假设（X，d）是一个完备度量空间，S（t，s）t≥s（t，s∈R）是一个映射集族，且满足：

（a）对所有τ≤s≤t有

S（t，s）S（s，τ）u ＝ S（t，τ）u；

（b）S（t，s）u关于t、τ和u 都是连续的；

（c）对t∈R，S（t，t）是X 中的恒等映射，则称S（t，s）为（X，d）上的一个过程．

设（x（t，s；x0，y0），y（t，s；x0，y0））是系统（6）在初值条件x（s）＝x0，y（s）＝y0下的解，则可知S（t，s）（x0，y0）＝ （x（t，s；x0，y0），y（s，t；x0，y0））是R2上的一个过程．

定义1．2［13］X 的子集族｛K（t）｝t∈R是拉回吸引的，如果对每一个有界集D满足

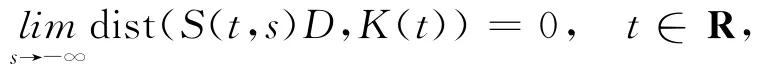
定义1．3［13］X 的子集族｛B（t）｝t∈R是关于过程S的不变集，若

定义1．4［13］紧集族是关于过程S的全局拉回吸引子，如果它是不变的、拉回吸引的，并且是最小拉回吸引（若是另一个闭的拉回吸引集族，则对t∈R有A（t）C（t））．

定理 1．5［13］存在一个全局拉回吸引子，当且仅当存在紧的拉回吸引集族

为研究系统（6）的渐近行为，给出与之相关的logistic方程及其一些有用结论．

考虑logistic方程

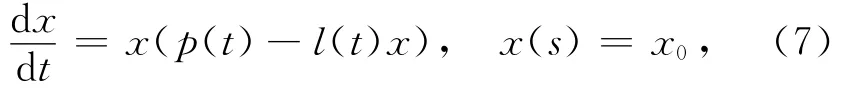
其中，p（t）＞0，l∈C0（R）．记该方程的解为θ［p（·），l（·）］（t，s；x0），经过计算可以得到

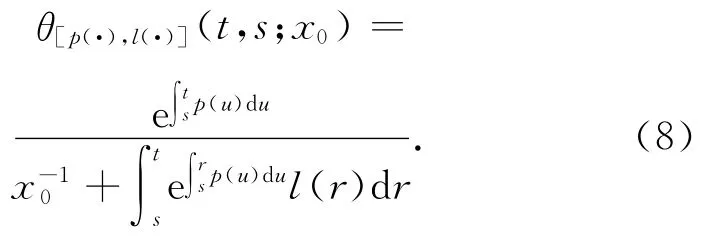
定理1．6［14］给定x（s）＝x0＞0，则存在（7）式的唯一正解θ［p，l］（t，x；x0）对t＞s是严格正的，并且θ［p，l］（t，x；x0）关于p 单增，关于l单减．

定理1．7［13］（7）式的解有以下性质：

（a）若p（t）→p＞0，且l（t）→0（t→∞），则θ［p，l］（t，s）→∞（t→∞）；

（b）若ps（·）→p＞0（s→－∞）（在紧子集R上一致），则存在

的解α：R→R，

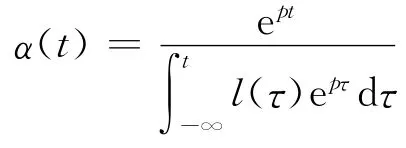
使得

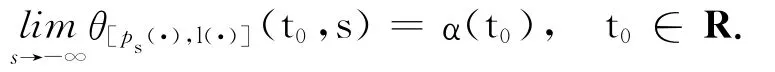
关于非自治系统（6）解的性质有如下结果．

定理1．8 给定x（s）＝x0＞0，y（s）＝y0＞0，则系统（6）存在唯一的解

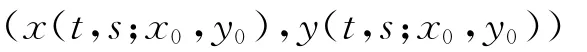
对所有t＞s严格为正，且

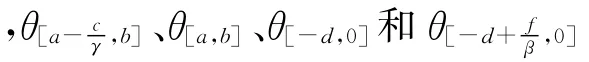
其中由（8）式给出．

证明 令

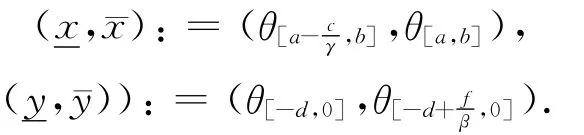
根据文献［11，13－14］，系统的向前持久性即指对任意初始值x（s）＝x0＞0，y（s）＝y0＞0，它的解 （x（t，s；x0，y0），y（t，s；x0，y0））在某一时刻后进入到一个正的严格有界紧集；系统的拉回持久性则是指存在正的与时间t相关的拉回吸收集族，并且是有界的．下面给出具体的定义．

定义1．9［12］系统（6）称为向前持久的，若存在正常数δ、Δ，0＜δ＜Δ，使得对系统（6）的所有拥有正的初始值的解满足

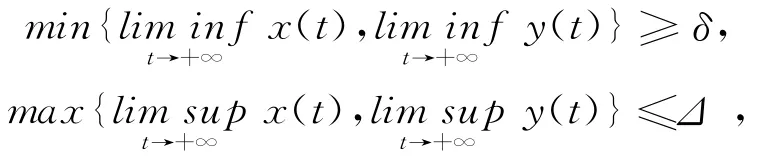
若有一个拥有正的初始值的解满足则系统（6）是非持久的．

定义1．10［14］系统（6）称为拉回持久的，若存在时间依赖集族｛U（t）｝t∈R2，满足：

（a）U（t）吸收所有 R2中的有界集；

（b）存在ε＞0，使得对所有t∈R，满足｜U（t）｜＞ε．

2 非自治系统的渐近性态

2．1 向前渐近行为 考虑到系统的生物因素，下面只考虑拥有正初始条件的解（x（t），y（t）），即满足x0，y0＞0的解．对R上的有界连续函数b（t），记

证明 对任意正的初始条件x（s）＝x0＞0，y（s）＝y0＞0，由定理1．8可知存在系统（6）唯一的解（x（t，s；x0，y0），y（t，s；x0，y0）），且满足

其中

令V＝fx＋cy，则

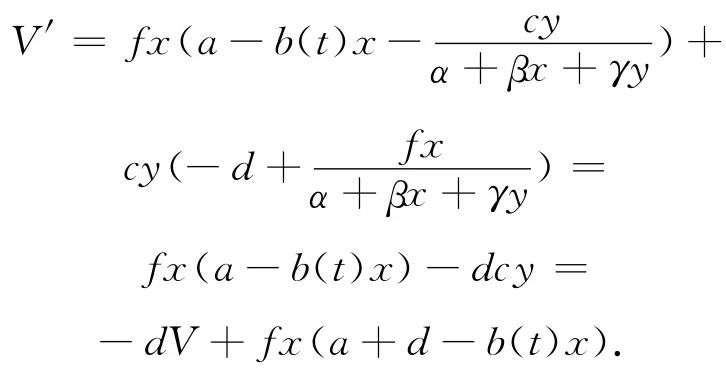
由

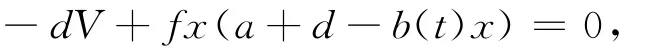
得

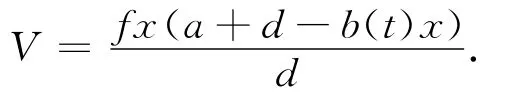
又由（10）式可得

因此

由（11）式有

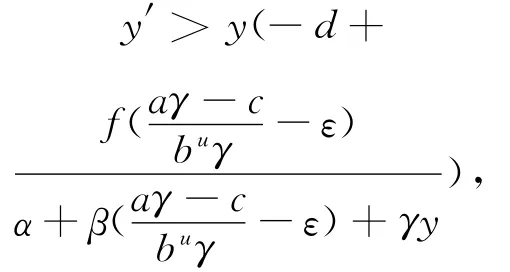
这里当t充分大时，ε＞0充分小．由

可得

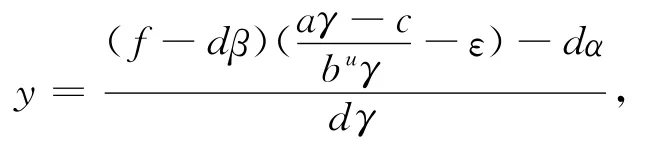
由条件可选择充分小的ε，使

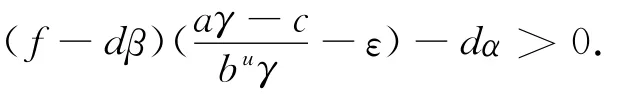
由此可推出

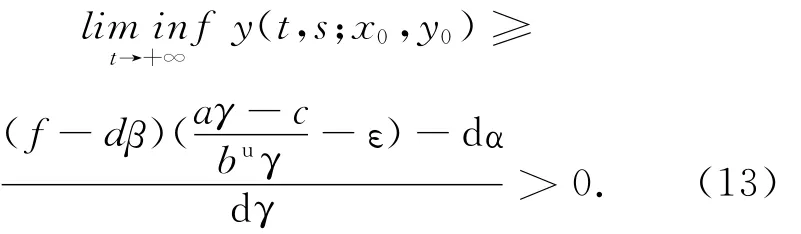
结合（10）～（13）式，系统（6）是向前持久的．

定理2．2 若βd＞f，则limy（t，s；x0，y0）＝

t→＋∞0．

证明 由定理1．8有

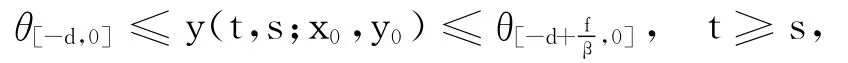
其中

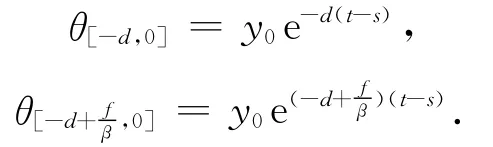
当βd＞f时

故

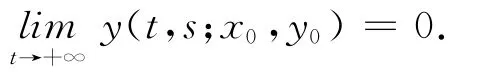
其中

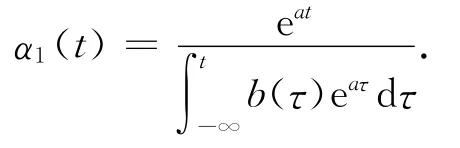
对微分方程

进行放缩，得到方程

当s→－∞时，有

由于

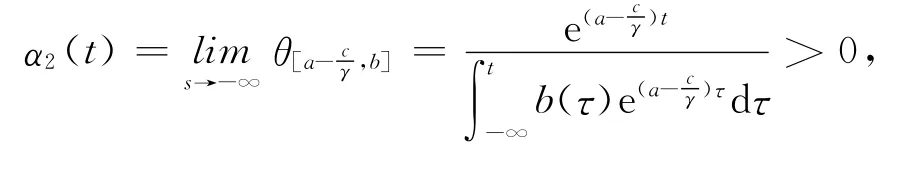
是可积的，根据函数的比较原理可知，存在β1（t）使得

因此，在R2中存在半径为

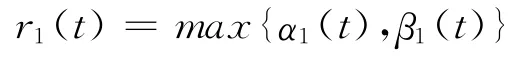
的球B（t）＝BR2（0，r1（t））是过程S（t，s）的拉回吸收集．故存在 R2中的紧的拉回集族｛B（t）｝t∈R．根据定理1．5可知存在一个全局拉回吸引子｛A（t）｝t∈R．

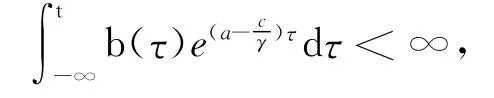
定理2．4 若且（f－dβ）α1－dα＞0，则系统（6）是拉回持久的．

其中

令

则有

由定理2．3，存在T（t，x0，y0）∈R使得

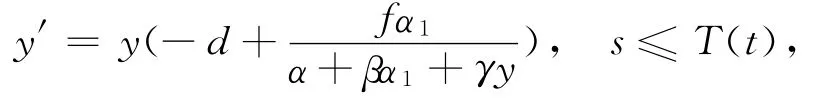
由

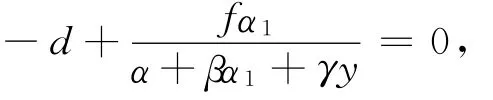
可得

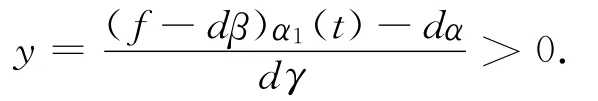
令

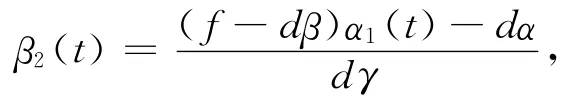
因此有

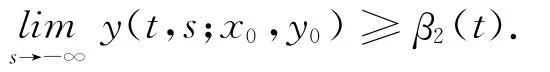
取

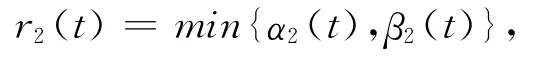
令

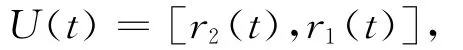
则U（t）吸收R2中的所有有界集，且满足0，故系统（6）是拉回持久的．