基于小波包能量的地基土对框筒结构地震损伤影响试验研究

沈 超， 钱德玲

(合肥工业大学 土木与水利工程学院，合肥 230009)

土-结构动力相互作用体系长期以来一直是国内外地震工程的研究热点课题。文献 [1-3] 表明：在地震作用下土-结构相互作用体系通过地基土的能量耗散减小了上部结构的动力响应和振动基频。但现有研究成果中的上部结构形式较为简单，多为单自由度体系或多自由度框架结构。对于实际高层框筒结构建筑，其地基土对上部结构的地震响应影响研究却较为少见。相比结构振动反应量的最值分析，小波包能量分析不仅能通过振动波形分解、小波包系数和频带能量反映结构的振动强度、基频和持时，还能通过能量变异最值指数反映结构的损伤情况。因此，采用小波包能量理论研究土-框筒结构高层建筑动力相互作用体系的地震响应具有十分重要的意义。

曹一龙等[4]采用小波包能量变异最值指数法对某八层混凝土框架结构振动台试验模型进行了损伤评定。中国生等[5]通过小波包能量分解理论，建立了爆破冲击波作用下考虑振动强度、频率和持时的建筑物结构安全评估判据。Suarez等[6]通过小波包能量分解计算得到了不同烈度地震作用下某新型软钢阻尼器的能量耗散特点，并结合能量变异最值指数分析了地震作用下安装该新型阻尼器的混凝土框架结构损伤情况。

1 结构损伤的能量指标定义

1.1 小波包分解和小波能量

小波包分解是基于小波变换的一种信号分解精细算法，该算法不仅具有小波变换的信号低频部分精确分解的优点，还能同时对高频部分精确分解，从而大大提高信号分解的完整性。

假定某振动信号f(t)经过小波包的j层分解，每个分解信号x(t)可表达为[7]

(1)

其中，

(2)

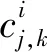
(3)

将分解信号x(t)的平方在无限域上积分即可得到信号f(t)的总能量

“那以后有机会再讲，我还是将那个男人的故事说完吧。S的前妻好像不止一个，但小说家没交待清楚，也许小说家也没有搞清楚。那个男人又不是小说家塑造的人物。这可能是那个男人的隐私，超出了小说家的掌控。当然，跟S有染的异性之多就难以尽数了。”

(4)

(5)

(6)

1.2 能量变异最值指数

在地震荷载作用下，结构的损伤必然导致结构固有特性的变化，从而使得结构各频带能量发生重分布。通过对比损伤前后各频带能量的最大值，可直观的反应结构的损伤程度变化。定义能量变异最值指数为

(7)

2 振动台试验简介

2.1 模型的设计与制作

为使研究结果能够更准确地反应地震作用下土对实际高层框筒建筑的损伤影响，试验模型选用某41层框架-核心筒高层建筑作为模拟对象。采用抽层的方法对原型结构进行简化，将各个标准层中相邻的上下楼板抽去，并将所抽去楼板的恒活荷载平均分配至相邻的上下层楼板，抽层过程如图1所示。根据强度和刚度等效原理对柱和核心筒截面进行修正，并采用Buckingham π定理确定模型各参数的相似比例(见表1)。最终将41层的原型结构简化为了缩尺比例为1/50的20层试验模型[8-10]。

表1 模型相似比例

简化后的试验模型上部结构高度为3.566 m，下部结构为3×3的群桩基础(见图2)，圆桩桩径0.08 m，桩长0.72 m，承台板尺寸为0.92 m×0.92 m×0.1 m的立方体。模型上部结构主要构件尺寸，见表2所示。模型材料选用与原型建筑材料力学性能相近的微粒混凝土、镀锌铁丝和铁丝网分别模拟原型建筑的混凝土、纵筋和楼板钢筋网[11-12]。

试验采用柔性圆筒状土箱装填试验用土，相比刚性土箱和层状剪切型土箱，柔性土箱能最大程度的降低“模型箱效应”。该土箱直径为3 m，土箱内试验用土自下而上分别为0.5 m厚砂土、0.5 m厚砂质粉土和0.1 m厚粉质黏土。土箱的构造和试验用土的粒径，如图3和图4所示。

图1 抽层过程Fig.1 The process of model simplifying

图2 模型下部群桩基础Fig.2 The view of the grouped piles foundation

楼层层高框架柱截面尺寸角柱边柱梁截面尺寸主梁次梁楼板厚度剪力墙厚124055×5535×3545×3030×151560220655×5535×3545×3030×151560326455×5535×3545×3030×1515604～2016850×5035×3535×2025×151545

图3 土箱结构示意图Fig.3 The structure sketch of the soil box

图4 试验用土粒径曲线Fig.4 The particle size of soil

图5 土-结构相互作用模型Fig. 5 The soil-structure interaction model

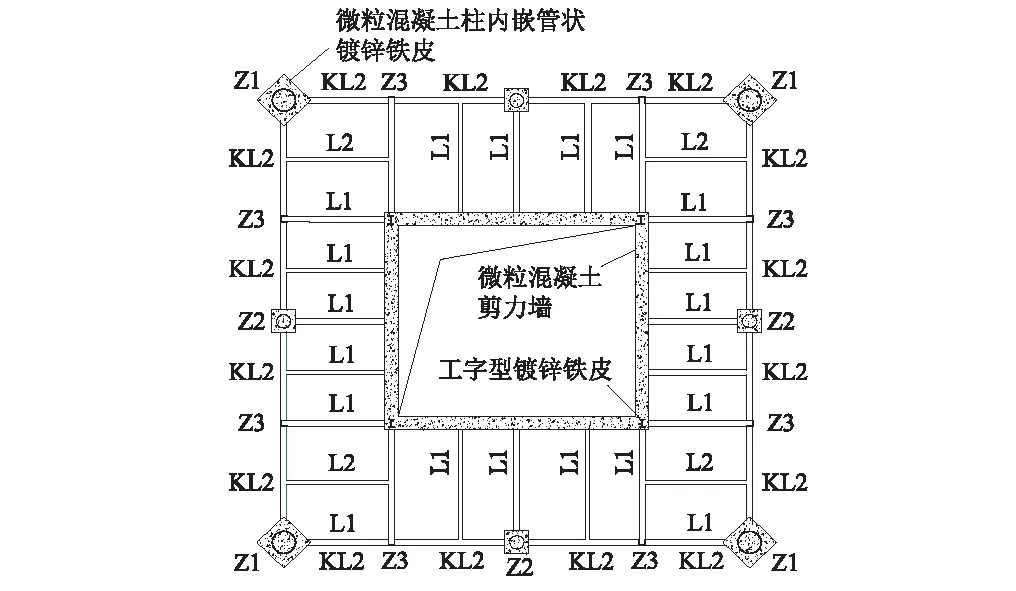
图6 楼层平面图Fig.6 The plane graph of floor

2.2 模型简化方法可靠性验证

采用大型有限元软件ANSYS建立了两个数值模型：原型结构和简化后的试验模型。通过对比两个数值模型的固有振型、固有周期，以及不同峰值加速度下的最大层间位移和最大层间位移角来验证该简化方法的可靠性。

图7给出了两个数值模型的振型计算结果。由图7可知，两数值模型前5阶振型一致；前2阶振型分别为沿Y轴和X轴方向的平摆；第三振型为扭转振型；第4、第5阶振型分别为沿Y轴和X轴方向具有一个反弯点的摆动。将两个模型的固有周期、最大层间位移和最大层间位移角进行对比，统计结果分别如表3～表5所示。固有周期最大误差为2.6%，层间位移的最大误差为5.42%，层间位移角的最大误差为8.56%。简化模型与原型结构的固有特性和动力反应较为接近，满足振动台试验精度的要求。因此，该简化方法是合理的，简化后的试验模型可作为试验的研究对象。

图7 振型图对比Fig.7 Comparison on the model shape

振型第1阶第2阶第3阶第4阶误差/%2.31.92.61.8

表4 层间位移的误差

表5 层间位移角的误差

2.3 测点布置

为获得上部结构在多向地震作用下的动力反应，两种模型上部结构沿高度方向均匀布置了27个加速度计。由于上部结构相同，两种试验模型的测点布置一致，加速度测点布置如图8所示。

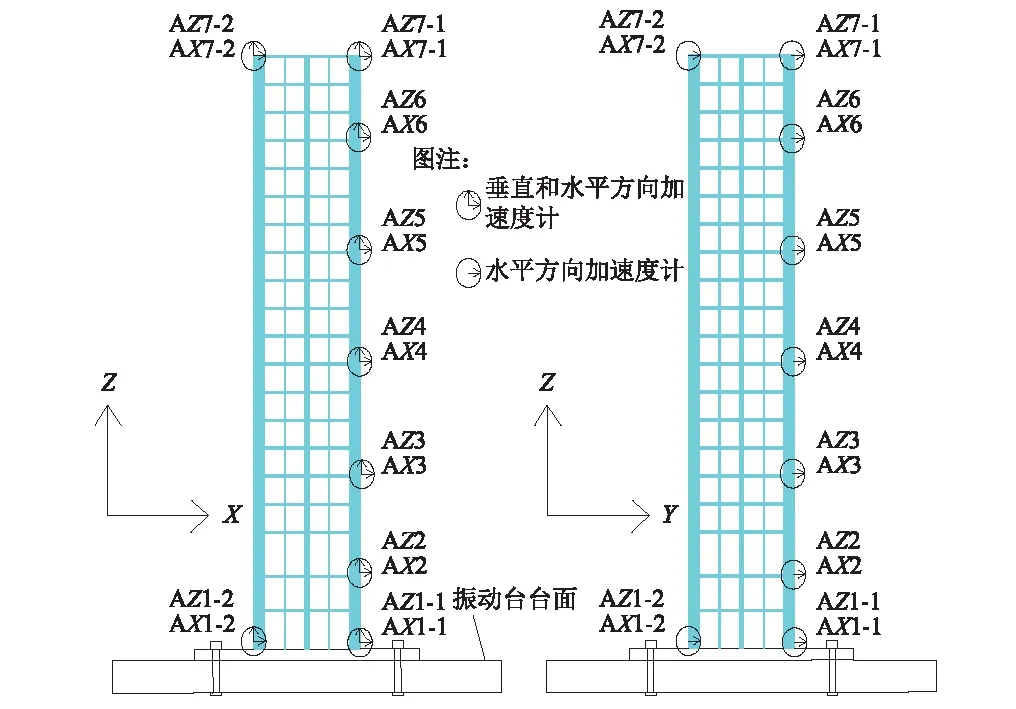
图8 测点布置示意图Fig.8 The sketch of the arrangement of gauges

2.4 加载工况

振动台的设备性能是影响试验成功与否的重要因素。本次试验采用同济大学引进的MTS模拟地震振动台，该振动台采用电液伺服驱动方式，具备三向六自由度试验能力，集台面编程、迭代补偿、数据分析和处理以及管理等功能于一体。最大承载重量25 t，最大驱动加速度为1.2g，能够模拟简谐振动、冲击以及地震作用，该振动台设备性能能够满足本试验的需求。

试验选用两条天然地震波(El Centro波和Kobe波)以及一条上海人工波作为振动激励。由原型结构与试验模型的加速度相似比例Sa=3.8可得，在模拟7度、8度和9度工程场地地震作用时，输入振动台的地震波峰值加速度应分别调整为0.38g，0.76g和1.14g。FB和SSI两个试验模型的加载工况完全相同，试验加载工况详如表6所示。

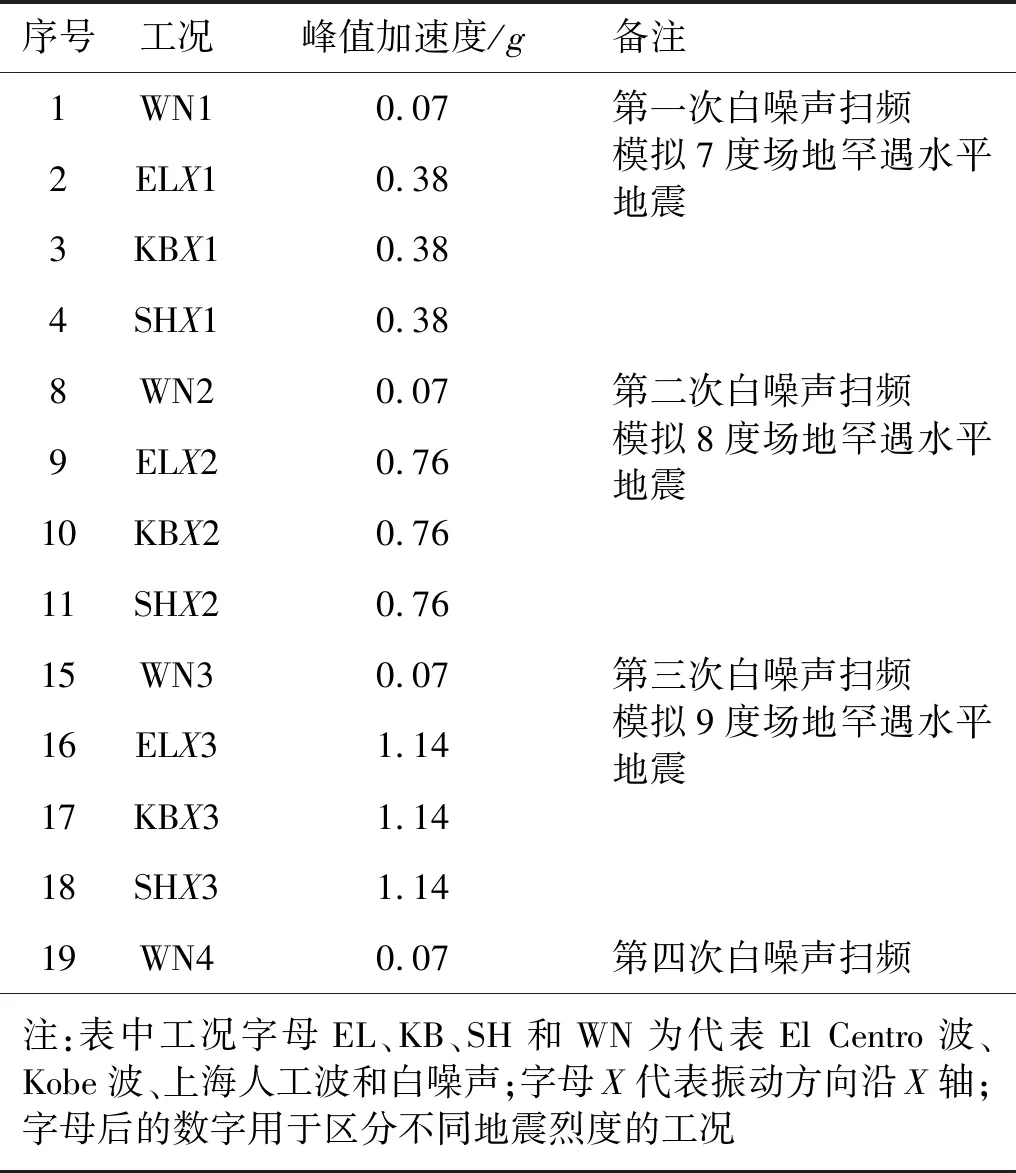
表6 加载工况

2.5 破坏现象

试验模型经历了加速度峰值从0.38～1.14g不断增大的过程，结构破坏现象简述如下：

(1)7度罕遇水平地震作用后，FB模型无损伤发生，SSI模型上部结构中部的外框架角柱发生宽度约为1 mm的水平裂缝，核心筒和群桩基础均未出现明显裂缝。

(2)8度罕遇水平地震作用后，FB试验模型的外框架柱底部发生宽度为1 mm的水平裂缝，核心筒无破坏现象；SSI试验模型的群桩桩身出现约为1 mm的水平细微裂缝(见图9)，上部结构中部的外框架柱水平裂缝未发生明显扩大。

(3)9度罕遇水平地震作用后，FB试验模型的外框架柱底部水平裂缝继续延伸，同时，核心筒出现宽度约为1 mm的水平裂缝(见图10)；SSI试验模型的裂缝无扩大趋势，受损情况与8度罕遇地震作用结果基本一致。

图9 桩基的破坏Fig.9 The failure in piles

图10 框架柱与核心筒的破坏Fig.10 The failure in frame column and core tube

3 试验数据处理与分析

3.1 分解信号波形分析

采用MATLAB软件中Daubechies 15小波函数对FB和SSI两个试验模型的加速度采样信号进行小波包2层分解[13-14]。由于各工况采样信号的小波包分解结果均呈现相似的趋势结果，鉴于篇幅有限，仅给出9度罕遇El Centrol波作用下FB和SSI试验模型结构顶部沿X轴方向采样信号的分解结果(见图11)。

图11 FB和SSI模型采样信号分解Fig.11 Sampling signal decomposition of the FB and SSI models

由图11可知，相比FB模型采样信号的分解波，SSI模型分解波的加速度峰值明显较小，这是土对振动能量的耗散使得SSI上部结构振动能量减小的结果。高次分解波的波形呈现为逐渐衰减的“拍”波形式，其峰值加速度量级极为微小，且1次波的小波包系数和频带能量(见图12)均接近于1，说明高次分解波均为随机噪声波。因此，试验模型的振动主要由1次波控制，将采样信号进行2层小波包分解是合理的。

图13给出了在9度罕遇El Centrol波作用下，FB和SSI两个试验模型不同楼层的总能量归一化比例结果。SSI模型各楼层总能量之和为0.044 J，远大于FB模型各楼层总能量之和0.006 J。FB模型各楼层的总能量随楼层高度的增大而增大，而SSI模型各楼层的总能量随楼层高度的增大呈现先减小后增大的趋势。上述现象表明，相比FB模型，SSI模型的土耗散了6/7的地震能量，从而使得上部结构所吸收的能量以及振动强度大幅减小。同时，SSI模型改变了能量沿楼层高度的分布。

图14给出了在9度罕遇El Centrol波作用下，FB和SSI两个试验模型不同楼层的加速度1次分解波。通过对比可知，SSI试验模型第1层～第3层的峰值加速度略大于FB模型，其它楼层的的峰值加速度则明显小于FB模型；FB模型的峰值加速度随楼层高度的增大而增大，SSI模型的峰值加速度随楼层高度的增大呈现为先减小后增大的趋势。上述现象表明，土对结构的动力响应有减小的趋势，但结构沿高度方向动力响应变化的趋势却与刚性基础有明显差别。

图12 分解波能量Fig.12 The energy of decomposition wave

图13 不同楼层总能量对比Fig.13 Comparison on the total energy of different floors

3.2 分解信号频谱分析

采用等能量的白噪声对两个试验模型进行扫频，从而获取模型在地震作用下固有特性的变化[15-16]。FB和SSI模型各测点白噪声1次分解波的频谱区间、主频率、主频率变坏百分比以及小波包系数统计结果，如表7所示。

由表7可知，两试验模型在各工况下的小波包系数接近于1，表明两个试验模型在地震激励下主要呈现为基频振动。为受损前FB模型的基频为7.12 Hz远大于SSI模型的基频3.28 Hz，表明考虑地基土的能够降低结构振动的基频。随着地震烈度的增大，两试验模型的上部结构基频均呈现降低的趋势，表明结构在地震作用下不断发生破坏。9度罕遇地震作用下FB模型的基频降低39.61%，而SSI模型的基频仅降低14.02%，表明通过地基土的地震能量耗散，SSI模型上部结构的破坏明显小于FB模型。

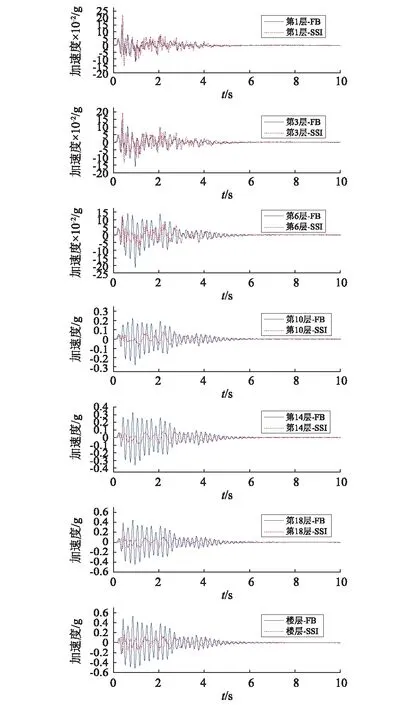
图14 不同楼层1次波对比Fig.14 Comparison on the 1st wave gauged at different floors

工况1次波频谱区间/Hz基频/Hz基频变化百分比/%小波包系数WN1-FB0～12.07.1200.999 917WN2-FB0～12.06.3311.100.999 920WN3-FB0～12.05.5122.610.999 946WN4-FB0～12.04.3039.610.999 878WN1-SSI0～12.03.2800.999 905WN2-SSI0～12.02.969.760.999 886WN3-SSI0～12.02.9111.280.999895WN4-SSI0～12.02.8214.020.999 966

3.3 能量变异最值指数分析

图15和图16分别给出了不同烈度地震作用下FB和SSI试验模型不同楼层的能量变异最大值指数(Maximum Energy Variation Index, MEVI )[17-18]。由图15可知，FB模型不同楼层的MEVI随地震烈度的增大而增大，8度罕遇地震作用后MEVI增幅最大，沿楼层高度方向的结构底部MEVI最大。表明FB模型在地震作用下上部结构受损程度随地震烈度的增大而增大，结构受到8度罕遇地震作用后损伤变化最为明显，沿楼层高度方向上部结构底部的最易发生损伤。

由图16可知，SSI模型不同楼层的MEVI随地震烈度的增大并未产生明显的变化，沿楼层高度方向结构中部的MEVI显著大于其它各楼层。表明SSI模型在地震作用下，沿楼层高度方向的结构中部受损最为严重，上述分析结果与试验现象也是相吻合的。

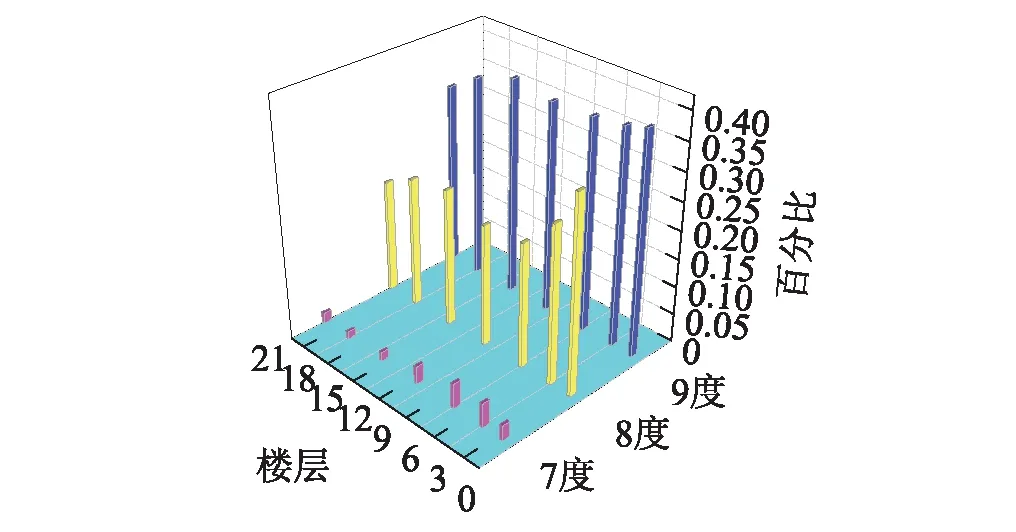
图15 FB模型能量变异最值指数Fig.15 The maximum energy variation index of the FB model

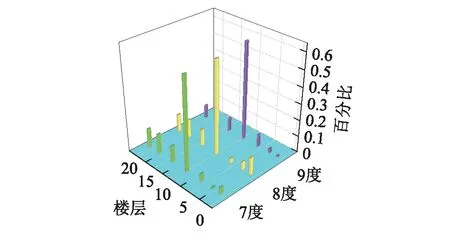
图16 SSI模型能量变异最值指数Fig.16 The maximum energy variation index of the SSI model

4 结 论

本文采用振动台试验的方法从小波包能量的角度研究了土对高层框筒结构震动响应的影响。通过对比FB和SSI两种试验模型在不同烈度地震作用下上部结构的能量分布、振动基频变化以及易损伤部位的差别得到以下结论：

(1) 在地震作用下，经土体的能量耗散SSI体系上部结构的峰值加速度、振动基频以及所吸收的能量相比FB体系显著降低。

(2) FB体系上部结构所吸收的地震能量随楼层高度的增大而增大，而SSI体系则随楼层高度的增大呈现先减小后增大的趋势。

(3) FB体系的损伤程度随地震烈度的增大而增大，上部结构的底部最易发生损伤；SSI体系的损伤程度随地震烈度的增大不明显变化，上部结构的中部最易发生损伤。