冶金法提纯多晶硅退火工艺优化的数学模型分析与试验验证
2019-08-31朱徐立吴虹琼
朱徐立 徐 隆 苏 骑 吴虹琼
(1 厦门城市职业学院机械与自动化工程系,厦门 361000)
(2 美甘齐动(厦门)物料输送工程股份有限公司,厦门 361000)
(3 厦门理工学院软件工程学院,厦门 361000)
文 摘 冶金法制备多晶硅过程中,通过对不同退火温控方案进行数学建模,探求优化的退火理论温度控制函数与曲线。数学模型表明,对硅铸锭直接进行保温,依靠自然热平衡退火,会使内部应力大于产生位错的临界应力;采用加热元件对硅铸锭适当加热保温可减缓降温速率。通过比较,选择较低的退火温度1 236℃和较短的退火时间8.52 ks作为试验退火温控方案。试验验证表明,该退火方案得到的多晶硅铸锭目视裂纹较少,少数载流子寿命与电阻率具有明显优势。
0 引言
在冶金法(物理法)多晶硅铸锭的提纯中,多晶硅铸锭内部热应力的大小和分布与晶体缺陷息息相关,是影响产品质量的关键因素,并最终影响光电转换效率。通过温控进行热应力的控制涵盖了定向凝固与退火全过程,退火过程的工艺甚至对铸锭的成功与否起决定性作用。定向凝固完成后,如不作任何热处理,直接放由铸锭炉的炉温自然降至室温拆炉,硅铸锭内部冷热不均现象严重,上下表面的温度差异很大,可达380~430℃[1],造成热应力增大[2-3],极有可能产生大量位错,甚至使铸锭碎裂[4-5]。因此,合理而周全的退火措施是保证铸锭成功的必要手段,进而减少热胀冷缩现象,不但能避免裂锭,还能改善晶体生长和排列条件,在一定程度上降低位错概率。
退火工艺因定向凝固炉的不同而各异,大多数需要依据经验通过多次试验或试生产来制定[6-7]。对多晶硅铸锭退火过程的理论研究多是进行定性分析,而定量分析特别是退火过程的数学模型方面的研究还比较少,本文通过建立数学模型,可以方便地改变工艺参数,寻求合适的工艺方案,对减少试验次数、指导生产实践和降低成本有着重要的理论依据和参考价值。
1 数学建模
从节能、控制简便与降低热应力的角度出发,提出以下两种退火温控工艺进行数学建模分析:第一种退火工艺是在定向凝固结束后,在硅铸锭顶部、底部、侧壁均进行良好的绝热保温,使铸锭内部温度自然平衡达到一致的退火温度后,再缓慢降温至室温(该方案主要作为参照目的);第二种退火工艺是凝固完成后,利用炉体安装的加热元件,对硅铸锭进行适当补热,使铸锭内部热平衡过程更加舒缓。
1.1 针对第一种退火工艺的建模
退火工艺过程的数学描述为:设凝固完成后时间点τ=0,此时硅铸锭顶部初始温度为ta0,底部初始温度为tb0,由于凝固完成,相变过程结束,没有内热源产生,高低温面的热传导使退火温度tAnn介于ta0与tb0之间,因此,硅铸锭中必存在一个t=tAnn的等温面SAnn,并设该面高度为yAnn(图1)。

图1 退火初始温度分布Fig.1 Distribution of initial annealing temperature
由于ta0降至tAnn与tb0升至tAnn的时间相等,该过程满足一维瞬态热传导微分方程,有

式中,a为热扩散系数。
满足边界条件

式中,τAnn为退火时间;H为硅铸锭高度;λ为硅铸锭热导率。
1.2 针对第二种退火工艺的建模
从缓解退火过程中的热应力考虑,凝固完成后,用炉内加热元件对硅铸锭适当补热,使铸锭温度趋于一致的过程放缓,同时退火温度得到提高。设该补热功率为qa,该过程的数学描述同式(1),仅边界条件改变为
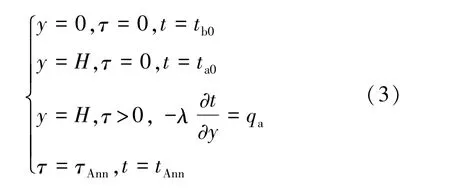
2 数学模型求解与讨论
2.1 第一种退火工艺数学模型求解
求解偏微分方程(1),除了式(2)定义的边界条件,由文献[8]可知,硅铸锭内部温度分布沿y方向服从抛物线t(y)分布。由于ta0、tb0初始值一定,在良好绝热条件下,热平衡后的tAnn为唯一确定值。对式(1)采用拉普拉斯(Laplace)变换,有

式中,s为Laplace算子。
式(4)的解为
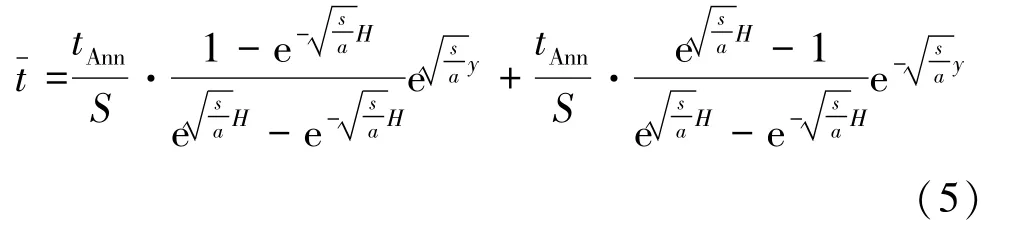
查拉普拉斯变换表[8],经过拉氏反变换,得到式(1)的解,有
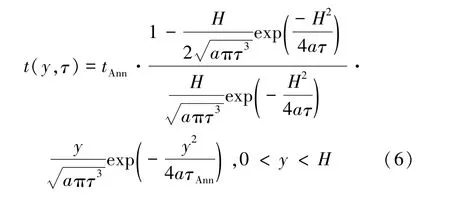
于是得到退火温控方案1的数学表达式。
2.2 第二种退火工艺数学模型求解
同理,可求解式(1)(3),得到的解见式(7)。

不同的是,式(6)只需要代入ta0、tb0、H等待定的已知条件,即可推导出该条件下tAnn和τAnn的值,而式(7)不但包含上述待定值,还包括补热功率qa这个待定参数,且tAnn和τAnn均为qa的函数,求解式(7)需要试算大量的qa值,过程繁琐。因此可以基于式(7)利用图像法求解。以ta0=1 400℃,tb0=1 000℃,H =0.5 m为例,可绘制qa关于tAnn和τAnn的函数图像,图2中,tAnn曲线与τAnn曲线分别有‘2’、‘3’两个交点,即得到两个退火方案。方案2:tAnn=1 236℃,τAnn=8.52 ks,qa=5.9 kW;退火温控方案3:tAnn=1 351℃,τAnn=11.283 ks,qa=10.3 kW。

图2 退火温度与退火时间的函数关系Fig.2 Function relation between annealing temperature and annealing time
2.3 求解结果讨论
综合文献[9-10]的研究和工程经验,认为多晶硅晶体内部区域应力>16.5 MPa时,该区域出现大量位错的概率较大,当应力≥42 MPa时,则极可能出现可见的明显裂纹。本文将16.5 MPa作为硅铸锭许用应力临界值,因此,tAnn与τAnn的取值均受许用应力(16.5 MPa)的约束,退火过程的热应力必须低于该值。
在第一种退火工艺中,同样令ta0=1 400℃,tb0=1 000℃,H=0.5 m,代入式(6)求解得tAnn=1 118℃,τAnn=6 980 s,作为退火温控方案1。在ProE软件中进行建模,硅铸锭宽度W =1 m,H =0.5 m,导入有限元软件的Transient Thermal与Structural模块进行计算,设置计算参数与边界条件:多晶硅的杨氏模量E =190 GPa,剪切模量G =89 GPa,泊松比μ=0.172,以 tAnn=1 118℃为计算终了温 度,以τAnn=6.98 ks作为计算时长,求解热应力,获得退火全程铸锭最大热应力的变化曲线(图3)。

图3 退火过程中硅铸锭应力变化曲线(方案1)Fig.3 Stress variation curves during annealing in silicon ingot(method 1)
很明显,图3中大部分时间内,热应力已超过临界值(16.5 MPa),最大热应力值为23.8 MPa。硅锭依靠自然热平衡进行退火,热应力较大,有大概率形成大量位错,甚至裂纹,该方案在理论上不可取。
同样的,对退火温控方案2和3进行数值分析,所获得的热应力变化曲线见图4。
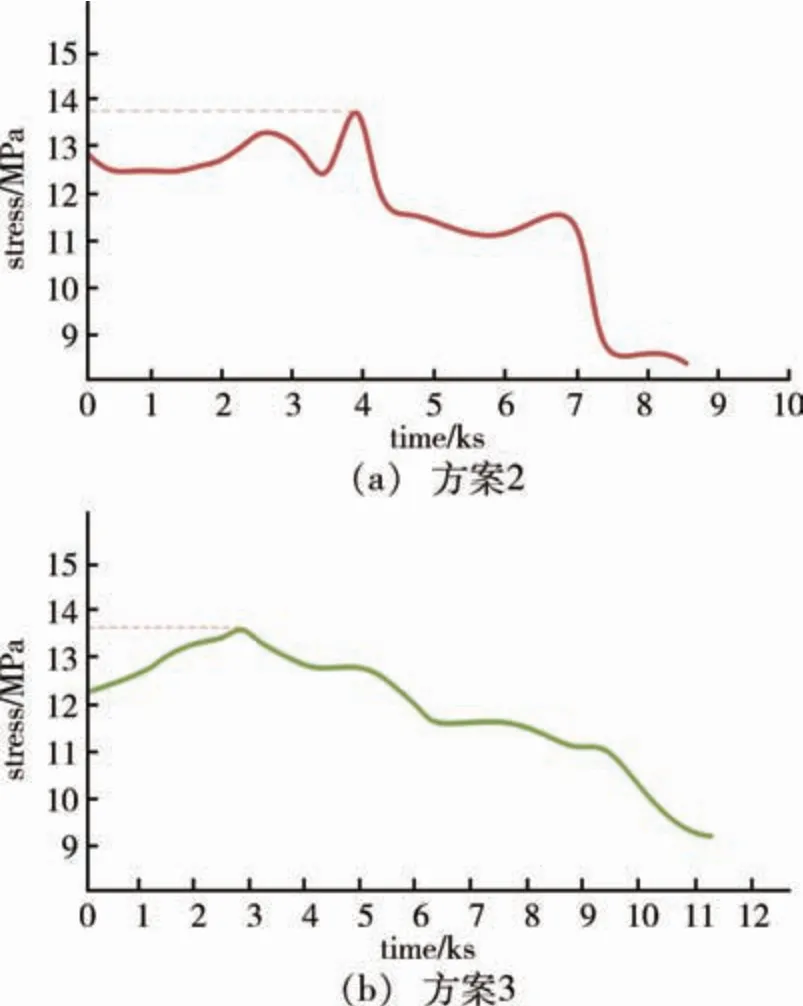
图4 退火过程中硅铸锭应力变化曲线Fig.4 Stress variation curves during annealing in silicon ingot
图4可以看出,方案2产生的最大热应力为13.72 MPa,方案3为13.6 MPa,均未超出临界值。将以上3种求解结果汇总于表1。
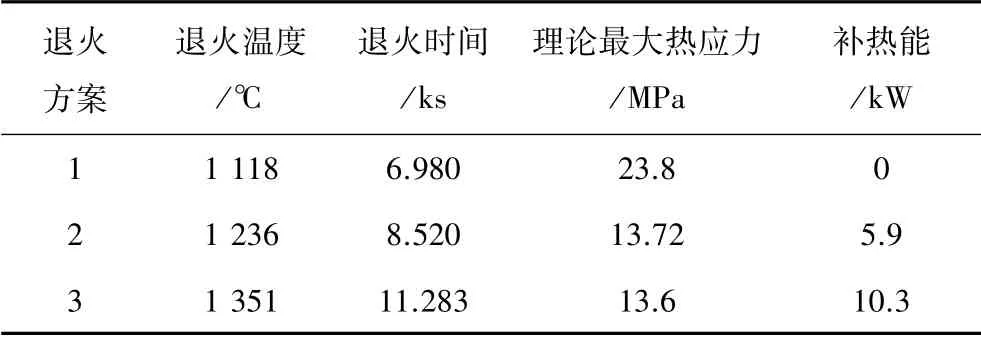
表1 三种求解结果的比较Table.1 Comparison of three solution results
一般来说,延长退火时间可以减少热应力,但过长的退火时间会降低生产效率,同时也增加能耗。虽然方案2的最大热应力略大于方案3,但退火时间和能耗明显降低,因此方案2为比较合理的理论退火方案。
3 实验
实验采用3N级多晶硅原料,使用本课题所研发的环形加热铸锭炉[11]进行铸锭与提纯。在凝固完成后分别采用上述方案1~3进行退火,比较所铸造的硅锭并检测主要指标。
3.1 实验结果
定向凝固结束后,经历3种不同退火方案后,得到的硅铸锭剖面如图5所示。可以看出,有贯穿硅铸锭上下底面的深层裂纹(退火方案1);采用退火方案2,没有明显的目视裂纹;而退火方案3在剖面右半部分则出现了局部浅表性裂纹。

图5 硅铸锭剖面Fig.5 Section of silicon ingot
3.2 分析与讨论
通过理论计算可知方案2、3全过程硅铸锭的热应力均未超过临界值,但在退火过程末期[图4(a)时间≥7 ks],方案2的热应力曲线有明显的大幅下降,因此,退火方案2对退火过程末期有更好地应力疏解作用。按照理论计算,退火方案3热应力不超过临界值,但得到的硅铸锭则产生了明显的浅表性裂纹,经过分析,推测造成退火方案3中硅铸锭出现裂纹的可能原因有以下两种。
(1)试验使用的本课题研发的铸锭炉(参见文献[11]中图7),该炉采用的是加热装置环形布置的方案,根据文献[11]的研究,为了节能和加强定向凝固时的对流传质,加热装置并未全面均匀布置。但由于硅铸锭本身热惰性的存在,在退火时间较长的情况下,环形加热形成的补热热场与理论情形(一维热场,温度梯度垂直向上)有一定偏差,造成对热应力的疏解较弱。
(2)温度传感器设置于铸锭炉上、下表面及侧壁位置(硅铸锭内部无法布置任何传感器),方案3的补热强度很大,在退火时间较长的情况下,根据传感器采集到的信号,自动控制系统“误认为”硅锭整体已经达到温度均匀,进而停止补热,而此时硅铸锭并未达到温度均匀,内部热应力还比较大。
通过在硅铸锭剖面上钻孔取样,取4个取样点(Sampling points)的检测值平均,作为该铸锭的检测指标,得到不同退火方案下的硅铸锭主要指标见表2。

表2 不同退火方案硅铸锭检测指标Table.2 Testing index of silicon ingot with different annealing schemes
由表2可知,不同的退火方案下,磷、硼以及主要金属杂质的含量基本相同,这是由于提纯杂质主要依靠定向凝固过程的分凝效应[12]实现,退火过程对杂质提纯影响极小。方案2的少数载流子寿命和电阻率指标最优,说明退火处理减小热应力有利于上述两种指标的提高。此外,方案1采用自然降温退火,因此能耗值最低,方案2、3采用补热退火,能耗均高于方案1,其中,方案3退火时间最长,能耗最高。
4 结论
经过对退火工艺的数学建模与求解,得到如下成果与结论:定向凝固完成后,须经历退火过程以降低硅锭顶、底面温差造成的内部热应力,经过理论推导,获得3种退火温控方案:tAnn=1 118℃,τAnn=6.98 ks;tAnn=1 236℃,τAnn=8.52 ks,qa=5.9 kW 以及tAnn=1 351℃,τAnn=11.283 ks,qa=10.3 kW。从热应力控制、节能和提高生产率的角度考虑,方案2在理论上比较合理。通过实验,该退火方案得到的多晶硅铸锭目视裂纹最少,少数载流子寿命与电阻率则明显优于方案1和方案3。本文推导的数学模型可以采用不同工艺参数代入求解,为冶金法提纯多晶硅的退火工艺的制定提供重要的理论参考。
