拓展解题思路 培养发散思维

朱小斌

一、教学背景

问题是数学的心脏，解题教学是数学课堂教学的重要形式之一。针对数学问题的特征，在课堂上引发教师与学生之间、学生与学生之间的讨论与交流，充分利用相关的数学知识和数学思维方法，寻找解决问题的策略和方法，拓展学生的解题思路，优化学生的思维品质，是解题教学的理想追求。

二、教学过程

出示例题：已知AC，BD 为圆O：x2+y2=4 的两条互相垂直的弦，垂足为M(1，)，则四边形ABCD 的面积的最大值为_______.

学生自己独立思考分析：要求面积的最值，先表达出面积的式子|AC||BD|。相互讨论后发现确实能表达出具体的式子。

求解：生：设两条互相垂直的弦所在直线方程为：

(说明：解决解析几何问题很大程度要求学生拥有一定的计算能力，这样的解题方法绝大部分学生都能掌握并运用起来，但能计算到最后，并且又能算对的，就会刷下去一部分学生了。)

师(轻轻询问)：同学们仔细再想想，完整了吗？有没有需要补充的地方？

生1(一拍脑袋)：设直线为点斜式方程时，事先应该确定直线斜率一定存在，那还有不存在的情况呢？

生2：当条两互相垂直的直线中有一条直线的斜率不存在时，另一条直线的斜率恰好为0，此时所求四边形的面积

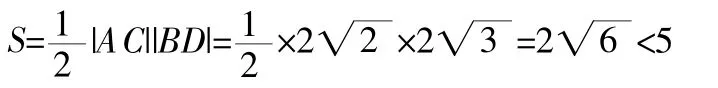
师(肯定)：解题思路清晰，用的是解析几何中常规的解方程组，韦达定理，弦长公式，需要花一些时间在计算上，有没有谁想过还会有其他省时的方法吗？

生3：我觉得几何法向来会比代数法要省时。

(学生共同合作探究几何法解决该面积问题。)

生：设圆心O 到直线AC、BD 的距离分别为d1，d2，

则d12+d22=|OM|2=3

所以，四边形ABCD 的面积

当4-d12=4-d22，即|AC|=|BD|时，等号成立。

师：根据图形，再结合不等式求解，少了许多的计算，这样求最值最省时又省力。

数学教学大纲指出：“数学教学中，发展思维能力是培养能力的核心。”思维能力的训练和发展是以暴露思维过程为前提的，是从暴露的过程中得到锤炼和提高的，所以例题探究讲解中，师生双方都必须充分暴露思维过程——解题思路的探索过程，解题方法和规律的概括过程，通过不断地“暴露”，不断地“创造”，将隐含着的数学思维方法源源不断地流入学生的头脑中，成为学生数学认知结构中的一部分，最终学会数学思维。

课后反思：在解决数学问题的教学过程中，常常需要运用已学过的数学知识，来培养学生分析问题和解决问题的能力；培养学生善于运用归纳、类比的思维方式和创新能力。

数学是研究数量关系和空间形式的一门科学。现代教育采取学生自主学习、合作探究的新型教学方式，树立“以人为本”的课堂教学理念。学生只有在自主探索的氛围中，才会有新的知识“生长”出来。数学学科核心素养的教学活动应该把握数学的本质，创设合适的教学情境、提出合适的数学问题，引发学生思考与交流，形成和发展数学学科核心素养。

《数学课程标准》明确指出：“数学学习过程充满着观察、实验、猜测、模拟、推断等探索性与挑战性活动，要重视从学生的生活实践和已有的知识中学习数学和理解数学。”通过高中数学课程学习，能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验；提高从数学角度发现和提出问题的能力、分析和解决问题的能力。