多巴胺磁性纳米粒子对Nisin的吸附特性

姜飞虹，宋子涵，牛 晨，张宇翔，魏建平，岳田利,*

（1.西北农林科技大学食品科学与工程学院，农业部农产品质量安全风险评估实验室（杨凌），国家农业综合测试工程研究中心（杨凌），陕西 杨凌 712100；2.西北大学食品科学与工程学院，陕西 西安 710000）

乳酸链球菌素（Nisin）是由乳酸链球菌产生的一种羊毛硫氨酸细菌素，能够有效地抑制革兰氏阳性菌[1-2]。Nisin无毒、无味且热稳定性较好，作为一种食品添加剂被广泛地应用在乳制品、蛋类、蔬菜、肉制品和鱼类等食品加工过程中，用来控制有害微生物的污染。然而，Nisin能够与液体食品中的蛋白质、糖和酯类等物质发生反应，降低了它的抑菌活性，因此在液体食品中鲜少应用。更重要的是，Nisin作为天然食品抑菌剂喷洒在食品表面，由于长期暴露在微生物表面，可能导致耐药菌的产生[3-4]。

因为磁性纳米粒子（iron oxide nanoparticles，IONPs）具有比表面积大、磁选速度快、吸附能力高和经济耐用等优点，已经成为一种重要的磁性材料，被广泛应用在蛋白的固定化、酶的分离纯化、重金属吸附、染料去除以及靶向给药等领域[5-6]。但是，因为磁性纳米粒子表面能较大，容易发生聚沉和氧化，在实际应用中应对其表面进行修饰[7]。多巴胺是一种通用的表面修饰剂，只需简单的步骤即可在材料表面形成聚多巴胺膜，合成方法和操作简单、经济，被广泛地应用于生物材料的表面修饰[8]。

生物物质的吸附是一个复杂的过程，当Nisin被吸附到磁性纳米粒子表面时，Nisin的结构和活性、吸附时间、吸附温度以及吸附剂的表面性质等都会影响到吸附的效率[6]。

综上所述，本研究通过测定不同温度和时间下多巴胺磁性纳米粒子（IONPs@pDA）吸附Nisin的含量，运用不同方程进行吸附动力学和吸附等温线拟合，系统研究多巴胺磁性纳米粒子吸附Nisin的机理和特性，以期为制备出既能保留Nisin抗菌活性又能够快速磁分离防止耐药菌产生的耦合体杀菌材料提供理论支持。

1 材料与方法

1.1 材料与试剂

Nisin（活力10 000 IU/mL）、多巴胺 美国Sigma公司；考马斯亮蓝 海博生物技术有限公司；磷酸盐缓冲液（phosphate buffered saline，PBS）（pH 7.2～7.4）、硫酸亚铁、硝酸铁、三乙胺、甲醇和十二烷基硫酸钠（sodium dodecyl sulfate，SDS）（均为分析纯） 西陇科学股份有限公司。

1.2 仪器与设备

RHD-160数显强力恒速电自动搅拌机 常州市人和仪器厂；Victor X3多功能酶标仪 美国PE公司；FD5-3真空冷冻干燥机 美国西盟公司；QYC-2102C恒温摇床上海福玛实验设备有限公司；UPHW-I优普系列超纯水器优普实业仪器（上海）有限公司；AUY220万分之一天平日本岛津公司。

1.3 方法

1.3.1 多巴胺磁性纳米粒子的制备

磁性纳米粒子的制备：分别配制0.1 mol/L硫酸亚铁和硝酸铁溶液，以体积比1∶1混合于大烧杯中，用机械搅拌器搅拌30 min。随后加入3 mmol/L SDS，继续用机械搅拌器搅拌30 min，逐滴加入三乙胺（体积分数5%），大力搅拌2 h，整个过程均在搅拌下进行。在3 h的搅拌下，悬液由深棕色变为纯黑色，即视为反应完成。磁性分离后重悬于超纯水中，用超纯水和甲醇反复清洗，经真空冷冻干燥，得到固体磁性纳米粒子，以备后续实验[9]。

多巴胺磁性纳米粒子的制备：将固体多巴胺加入到PBS（10 mmol/L、pH 8.5）中，用机械搅拌器搅拌溶解，再加入制备好的磁性纳米粒子，充分搅拌24 h。反应结束后，产物经磁性分离，重悬于超纯水中，充分搅拌12 h，经真空冷冻干燥得到多巴胺磁性纳米粒子，以备后续实验[10]。

1.3.2 多巴胺磁性纳米粒子吸附Nisin分析

1.3.2.1 Nisin标准曲线制作及含量的测定

用万分之一天平准确称取Nisin试剂0.010 0 g，用移液枪准确量取1 mL PBS（10 mmol/L、pH 6.86），充分溶解后作为Nisin标准溶液的母液。将母液依次稀释至质量浓度为0.006 0、0.005 0、0.004 0、0.003 0、0.002 0、0.001 0、0.000 5 mg/mL，即为Nisin系列标准溶液。

准确量取20 μL Nisin标准溶液和待测样品，加入100 μL考马斯亮蓝溶液，充分混合均匀并静置5 min，用酶标仪在595 nm波长下测定混合液的吸光度，绘制Nisin标准曲线，计算待测样品中的Nisin含量。每个样品设置3 个平行实验。

1.3.2.2 多巴胺磁性纳米粒子对Nisin的吸附动力学分析

用万分之一天平准确称取0.080 0 g Nisin固体粉末，用20 mL PBS（10 mmol/L、pH 6.86）溶解。再准确称取0.080 0 g多巴胺磁性纳米粒子，加入到Nisin溶液中，将混合物分别放置在温度为298、318、338 K的水浴锅中恒温振荡吸附，在吸附时间为0、5、10、30、60、90、120、150、180 min时，量取20 μL吸附溶液，磁性分离后测定Nisin含量。每个测定温度设置3 个平行实验。

测定Nisin含量后，计算9 个时间点所对应的Nisin吸附量Qt，以时间t为横坐标、吸附量Qt为纵坐标作图，得到不同温度下的吸附动力学曲线。

本实验选择了4 种动力学方程来进行吸附动力学过程的线性拟合，分别是Lagergren准一级反应动力学方程[11]、Lagergren准二级反应动力学方程[12]、Elovich方程[13]和内部扩散方程[14]。

Lagergren准一级反应动力学方程如式（1）所示。

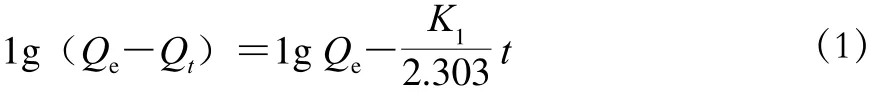
式中：K1为Lagergren准一级反应动力学速率常数/min－1；Qt为吸附时间为t时Nisin的吸附量/（mg/mg）；Qe为吸附达到平衡时Nisin的平衡吸附量/（mg/mg）；t为吸附时间/min。

Lagergren准二级反应动力学方程如式（2）所示。

式中：K2为Lagergren准二级反应动力学速率常数/（mg/（mg·min））；Qt为吸附时间为t时Nisin的吸附量/（mg/mg）；Qe为吸附达到平衡时Nisin的平衡吸附量/（mg/mg）；t为吸附时间/min。

Elovich方程如式（3）所示。

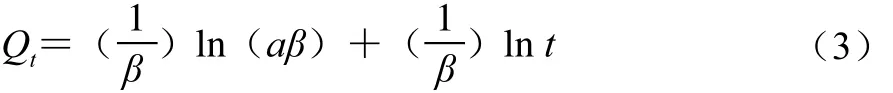
式中：Qt为吸附时间为t时Nisin的吸附量/（mg/mg）；α为反应初始吸附速率/（mg/（mg·min））；β为解吸常数/（mg/mg）。

内部扩散方程如式（4）所示。

式中：Qt为吸附时间t时Nisin的吸附量/（mg/mg）；Kd为吸附反应的内部扩散速率常数/（mg/（mg·min1/2））；I为边界层的厚度对吸附过程影响的常数/（mg/mg）。

1.3.2.3 多巴胺磁性纳米粒子对Nisin的吸附等温线分析

准确配制Nisin标准溶液，使其质量浓度依次为0.000 5、0.001 0、0.002 0、0.003 0、0.004 0、0.005 0 g/mL。用万分之一天平准确称取0.004 0 g多巴胺磁性纳米粒子，加入到1 mL配制好的Nisin溶液中，将混合物放置在温度分别为298、318、338 K的水浴锅中恒温振荡吸附，磁性分离后测定Nisin含量。每个测定温度设置3 个平行实验。

以吸附达到平衡时Nisin的质量浓度Ce为横坐标、吸附量Qe为纵坐标作图，绘制出不同温度的吸附等温线。吸附量Qt的计算如公式（5）[15]所示。

式中：Qt为吸附时间t时Nisin的吸附量/（mg/mg）；C0为吸附反应中Nisin的初始质量浓度/（mg/mL）；Ct为吸附时间为t时Nisin的质量浓度/（mg/mL）；V为反应时Nisin溶液的总体积/mL；m为加入的多巴胺磁性纳米粒子的质量/mg。

为了更深入地研究Nisin吸附反应过程中的平衡吸附关系，本实验选择了3 种吸附等温方程进行拟合，依次是Langmuir吸附等温方程[16]、Freundlich吸附等温方程[8]和Temkin吸附等温方程[17]。

Langmuir吸附等温方程如式（6）所示。

式中：Qm为单分子层趋于饱和时的理论吸附量/（mg/mg）；Qe为吸附达到平衡时Nisin的平衡吸附量/（mg/mg）；Ce为吸附达到平衡时Nisin的质量浓度/（mg/mL）；KL为朗缪尔常数/（mL/mg）。

朗缪尔吸附等温模型的另一种表达方式是用分离系数RL来表示，如式（7）所示。

式中：C0为吸附反应中N i s i n的初始质量浓度/（mg/mL）；KL为朗缪尔常数/（mL/mg）。

Freundlich吸附等温方程如式（8）所示。

式中：Qe为吸附达到平衡时Nisin的平衡吸附量/（mg/mg）；Ce为吸附达到平衡时Nisin的质量浓度/（mg/mL）；KF为Freundlich模型下Nisin的最大吸附量/（mg/mg）；bF为Freundlich吸附平衡常数/（mg/（mg·min））。

Temkin吸附等温方程如式（9）所示。

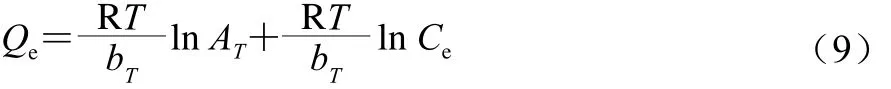
式中：Qe为吸附达到平衡时N i s i n的平衡吸附量/（mg/mg）；Ce为吸附达到平衡时Nisin的质量浓度/（mg/mL）；bT代表吸附强度/（J/mol）；AT为吸附平衡时的结合常数/（mg/mL）；R为理想气体常数（8.314 J/（mol·K））；T为绝对温度/K。

1.3.2.4 多巴胺磁性纳米粒子吸附Nisin的热力学分析

吸附热力学可以探究吸附反应温度对整个吸附过程的影响。热力学参数的计算公式如式（10）、（11）所示[18]。

式中：KL为朗缪尔常数/（mL/mg）；ΔG°为标准吉布斯自由能变/（kJ/mol）；ΔH°为标准焓变/（kJ/mol）；ΔS°为标准熵变/（J/（mol·K））；R为理想气体常数（8.314 J/（mol·K））；T为绝对温度/K。

1.4 数据分析

采用Origin 9.0软件进行相关图表的绘制以及模型的拟合。

2 结果与分析

2.1 多巴胺磁性纳米粒子对Nisin的吸附动力学分析结果

多巴胺磁性纳米粒子在不同温度条件下吸附Nisin的动力学曲线如图1所示。随着吸附时间的延长，磁性纳米粒子对Nisin的吸附量不断增加。吸附反应在前5 min时反应速率较高，5 min后吸附速率增长缓慢。这是因为随着吸附反应的进行，多巴胺磁性纳米粒子的吸附位点逐渐减少，导致Nisin的吸附速率逐渐降低，直至达到吸附平衡。在298、318、338 K的温度下，多巴胺磁性纳米粒子的最大吸附量分别为0.421 4、0.407 7、0.494 9 mg/mg。

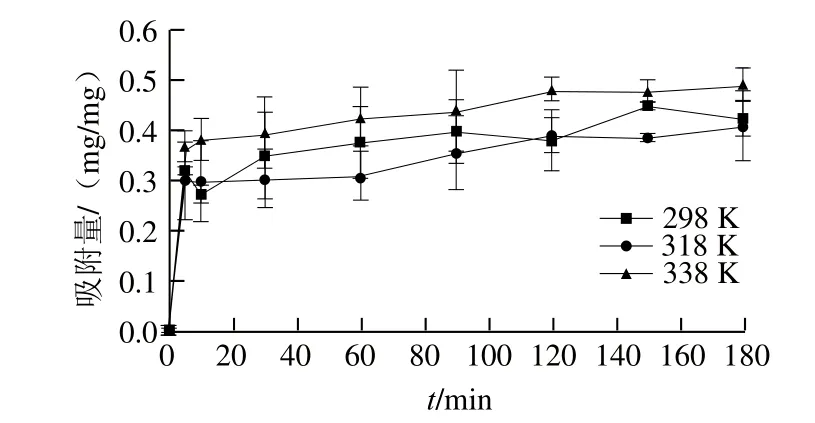
图1 多巴胺磁性纳米粒子吸附Nisin的动力学曲线Fig. 1 Adsorption kinetics of nisin on IONPs@pDA at different temperatures

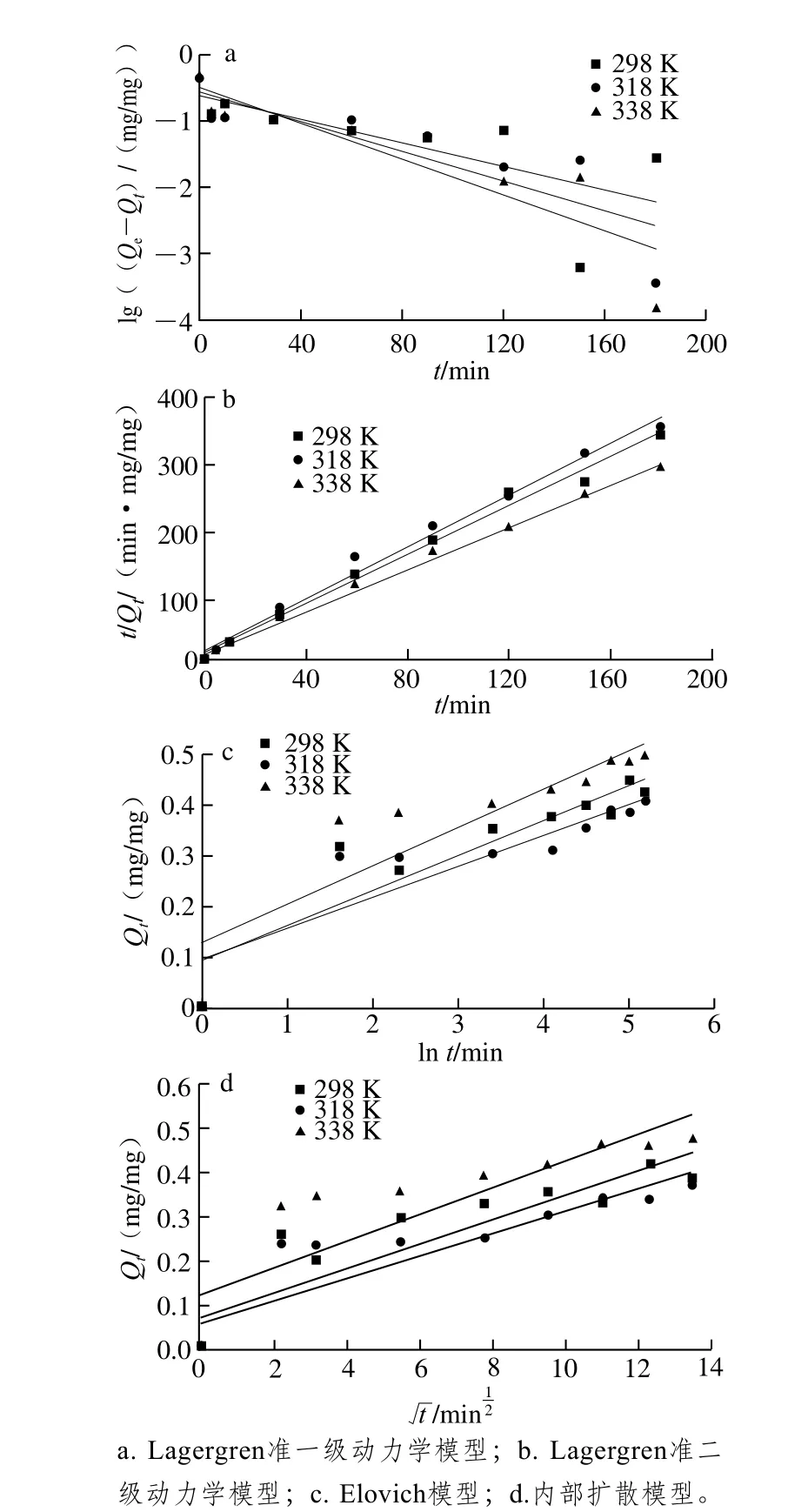
图2 多巴胺磁性纳米粒子吸附Nisin的动力学方程拟合曲线Fig. 2 Linear kinetic plots of nisin adsorption onto IONPs@pDA at different temperatures

吸附动力学研究通过线性方程的拟合，计算吸附过程中吸附质在固液界面上的吸附速率等重要参数[19]，了解吸附机理和吸附本质。本研究选择了4 种吸附动力学方程对吸附动力学过程进行拟合，结果如图2所示。

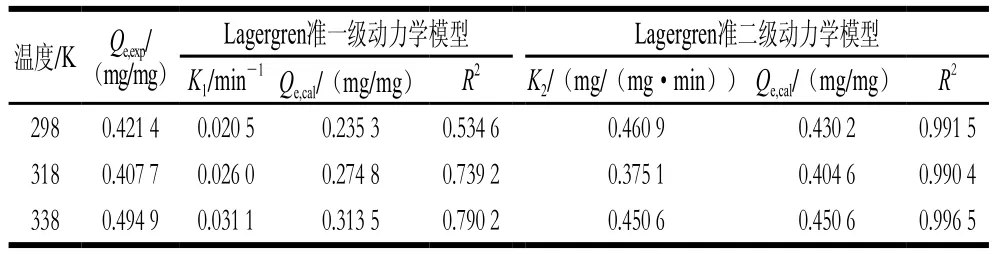
表1 Lagergren准一级、准二级吸附动力学方程的吸附速率常数、理论及实际平衡吸附量Table 1 Pseudo-first-order and pseudo-second-order adsorption rate constants as well as calculated and experimental Qe values

由表1可知，Lagergren准二级动力学方程的R2最高，理论吸附量与实际吸附量更接近。因此，多巴胺磁性纳米粒子对Nisin的吸附过程更加符合Lagergren准二级吸附动力学模型，吸附速率由吸附剂表面未被占用的吸附空位数目的平方值决定。多巴胺磁性纳米粒子对Nisin的吸附受化学吸附控制，且化学吸附占主导作用，吸附过程涉及吸附质与吸附剂间的电子共享或电子转移[20-21]。类似地，磁性锌铁氧体-海藻酸生物高分子复合材料对染料的吸附[22]、聚噻吩磁性纳米粒子吸附沥青[23]和磁性纳米粒子从水中吸附碱性蓝[24]的过程都符合Lagergren准二级吸附动力学模型，说明许多磁性纳米粒子对蛋白和染料等物质的吸附过程并非是简单的物理吸附，而主要受化学吸附控制。

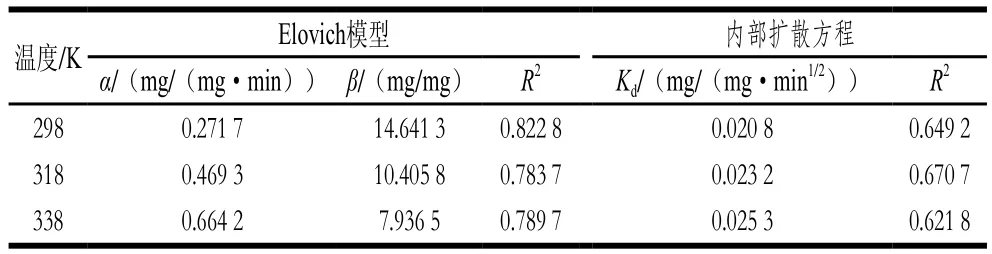
表2 Elovich方程和内部扩散方程基本参数及相关系数Table 2 Basic parameters and correlation coefficients calculated for Elovich and pore diffusion equations

Elovich模型一般用于模拟吸附速率，随着吸附温度的增加，初始速率常数α也会增大，因此实验中可以通过提高吸附温度来增加初始反应速率。如表2所示，通过比较R2发现，Elovich模型较内部扩散模型能更好地解释吸附过程，说明吸附反应速率和外部的不均匀扩散共同影响吸附过程[25]。如果内部扩散模型拟合结果是线性的，说明颗粒内扩散参与了吸附过程；如果拟合线经过原点，则说明颗粒内扩散是吸附反应的限速步骤。由图2d可知，内部扩散模型的3条拟合线均没有经过原点，说明内部扩散模型不能准确反映Nisin的吸附过程，且颗粒内扩散并不是Nisin吸附过程中的主要限速步骤[26]。

2.2 多巴胺磁性纳米粒子对Nisin的吸附等温线分析结果

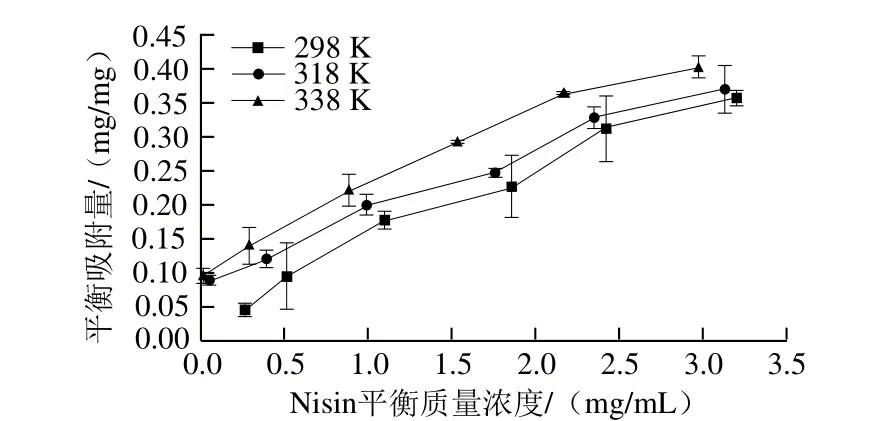
图3 多巴胺磁性纳米粒子在不同温度下对Nisin的吸附等温线Fig. 3 Adsorption isotherms of nisin onto IONPs@pDA with different temperatures

如图3所示，随着Nisin平衡质量浓度（Ce）的增加，平衡吸附量（Qe）也在不断增加。当Nisin平衡质量浓度增加到一定程度时，平衡吸附量增加缓慢或者不再变化，这是因为多巴胺磁性纳米粒子吸附位点有限，导致吸附量不再随着质量浓度的增加而增大。另外，由图3可知，平衡吸附量随着温度的升高而增大，表明多巴胺磁性纳米粒子对Nisin的吸附过程是吸热反应。

吸附等温线描述了特定温度下吸附质从液体介质到固体吸附剂的迁移过程[27]。本研究选择了3 种吸附等温方程，分别是Langmuir吸附等温方程、Freundlich吸附等温方程和Temkin吸附等温方程，对吸附等温线进行线性拟合，结果见图4a、b、c。依据拟合结果，得到拟合直线的斜率和截距，分别计算获得3 种模型常数（表3）。根据朗缪尔吸附等温模型计算相应温度下的分离系数RL，结果见图4d。

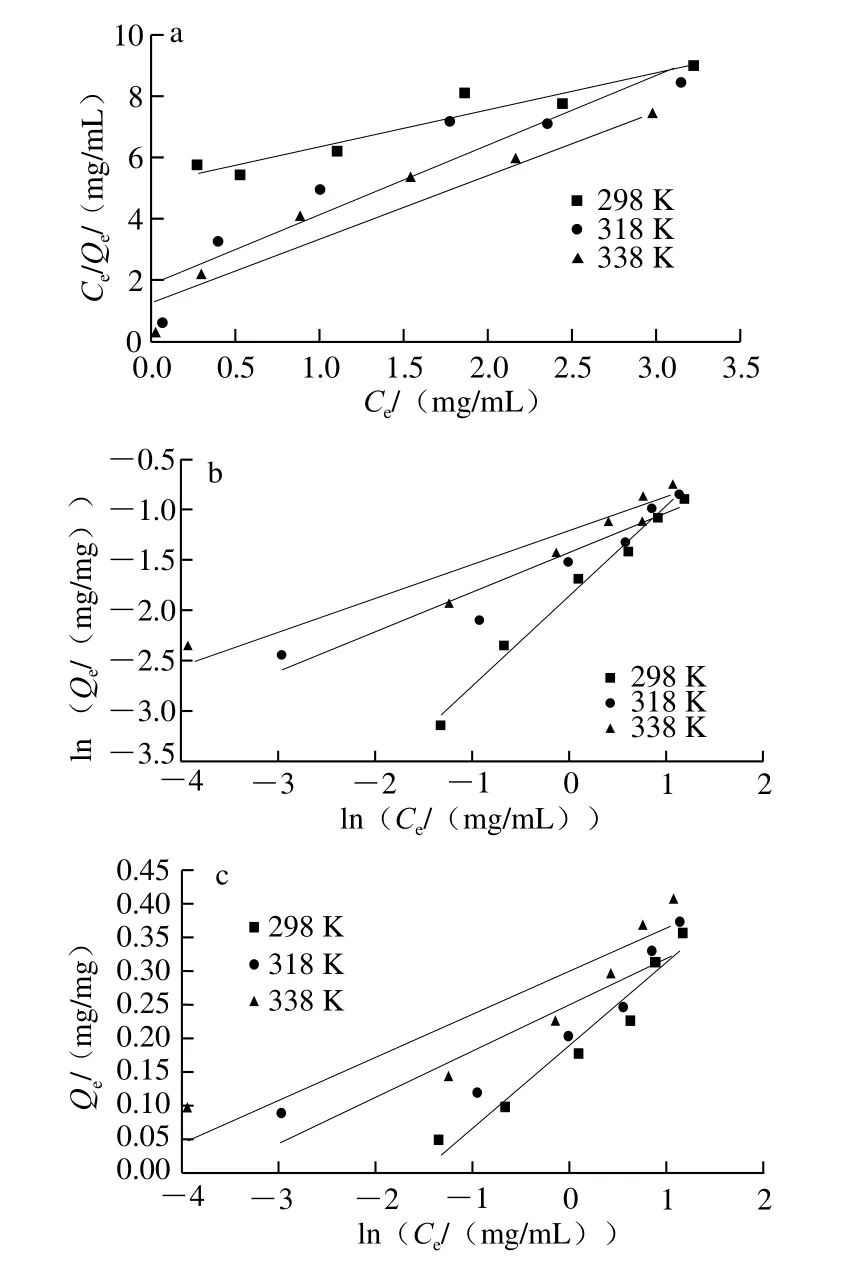
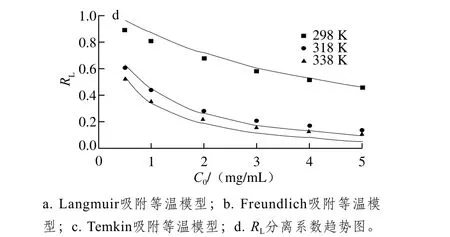
图4 多巴胺磁性纳米粒子吸附Nisin的热力学方程拟合曲线Fig. 4 Linear thermodynamic plots of nisin adsorption onto IONPs@pDA

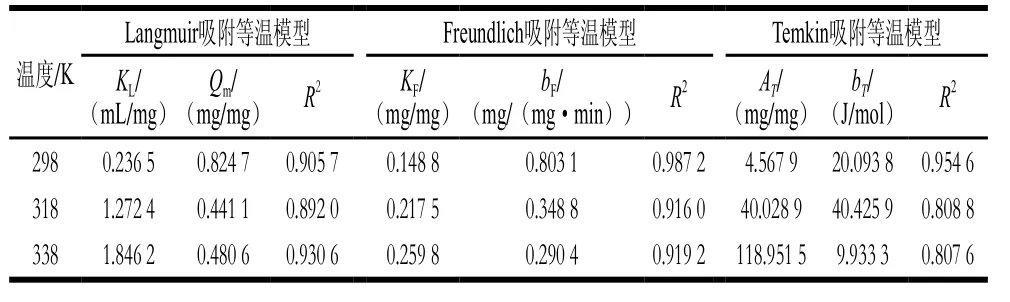
表3 多巴胺磁性纳米粒子对Nisin的吸附等温模型常数Table 3 Isotherm constants for adsorption of nisin by IONPs@pDA

Langmuir吸附等温方程是一个经验方程，它假设吸附是单层且均匀的过程，即反应具有恒定的焓和吸附活化能，用来描述吸附剂表面均匀时的吸附过程[28]。对于Langmuir吸附模型，KL能反映多巴胺磁性纳米粒子结合Nisin的稳定性，实验中KL随着温度的升高而增大，说明温度的升高提高了多巴胺磁性纳米粒子-Nisin耦合体的稳定性，更有利于吸附反应的进行。通过KL计算吸附反应的分离系数RL，根据RL可以判断吸附反应过程的难易程度（RL＞1，反应不易进行；RL=1，线性反应；0＜RL＜1，反应较易进行；RL=0，反应不可逆）[28]。如图4d所示，3 个温度下的RL均在0～1之间，代表吸附反应过程容易进行。Freundlich吸附等温模型是一个经验模型，用来描述吸附剂的多分子层不均匀吸附过程[29]。Freundlich模型中KF代表吸附剂的吸附能力，bF用来描述吸附发生的难易程度（bF＞1，反应不易进行；bF=1，反应不可逆；0＜bF＜1，反应较易进行）[30]。本研究中KF随温度的升高而增大，表明温度的升高提高了吸附剂的吸附能力，再次证明吸附过程是一个吸热反应。而bF均小于1且随温度的升高而降低，表明温度的升高使吸附反应越来越容易进行。Temkin吸附等温模型用于研究非匀质表面能系统中吸附剂与吸附质之间的相互作用[31]。AT是达到吸附平衡时的结合常数，随着温度的升高，AT逐渐增大，表明随温度的升高，多巴胺磁性纳米粒子与Nisin的结合作用逐渐增强。

通过比较表3中3 种模型的R2发现，Freundlich模型能够更好地描述多巴胺磁性纳米粒子对Nisin的吸附过程。说明本研究制备的多巴胺磁性纳米颗粒表面存在不均匀的吸附位点，并不是单一的单层、均匀吸附，反应是由各种相互作用引起的发生在吸附剂表面的多层不均匀吸附过程。吸附过程符合Freundlich模型的还有磁性海藻酸盐/氧化碳纳米管复合材料吸附阳离子染料[32]、壳聚糖磁性微球吸附结晶紫[33]和多羧酸多巴胺磁性微球吸附孔雀石绿染料[34]，这些研究结果表明，磁性纳米颗粒经过表面修饰后，表面作用位点分布不均匀，进而产生了多层不均匀吸附的现象。

2.3 多巴胺磁性纳米粒子对Nisin的吸附热力学分析结果

通过热力学结果分析能够判断吸附反应的自发性，了解吸附过程的难易情况[35]。根据公式（10）、（11）计算标准吉布斯自由能变（ΔG°）、标准焓变（ΔH°）和标准熵变（ΔS°）。如表4所示，298 K和318 K下吸附反应的ΔG°为正值，说明温度较低时，吸附反应不能自发进行，但是当温度为338 K时ΔG°为负值，说明反应可以自发进行。此外，吸附反应的ΔH°大于零，再次证明吸附过程是吸热反应，升高温度有利于吸附反应的进行，这与

2.2 节中吸附等温模型研究结果一致。而吸附反应的ΔS°大于零，表明吸附反应是一个熵增加过程，吸附过程中固液界面的混乱度增大。

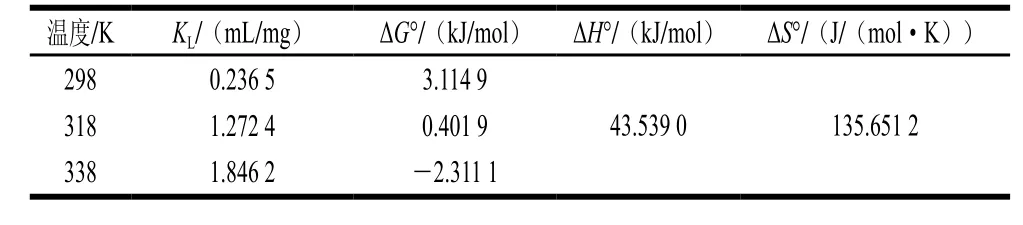
表4 不同温度条件下多巴胺磁性纳米粒子对Nisin的吸附热力学和活化能参数Table 4 Thermodynamic parameters and activation energy for the adsorption of nisin onto IONPs@pDA

3 结 论

本实验研究了多巴胺磁性纳米粒子对Nisin的吸附理论。吸附动力学与吸附等温线拟合结果表明，Lagergren准二级吸附动力学模型和Freundlich吸附等温模型能更好地描述吸附过程，说明多巴胺磁性纳米粒子对Nisin的吸附主要受化学吸附控制，且吸附反应是发生在异构表面的多层不均匀吸附。热力学分析结果表明多巴胺磁性纳米粒子对Nisin的吸附过程是吸热反应，Nisin的吸附量随着温度的升高而增大。说明多巴胺磁性纳米粒子能够有效地吸附Nisin。本研究结果为获得既保留Nisin抗菌活性又能够快速磁分离防止细菌耐药性产生的多巴胺磁性纳米粒子-Nisin耦合体提供了理论依据。