CO2捕集、运输、驱油与封存全流程不确定性优化研究

2019-08-30刘佳佳赵东亚

石油工程建设 2019年4期

刘佳佳，赵东亚

中国石油大学（华东）化学工程学院，山东青岛 266580

1 概述

随着全球经济快速发展，人们对化石能源的消费也不断增长，由CO2等温室气体造成的全球气候变化的威胁与日俱增，共同推进温室气体减排已成为全球性共识[1-2]。CO2捕集、运输、驱油与封存技术（CCUS）作为有效缓解CO2排放的关键技术引起了学术界和工业界的广泛关注[3-6]。

对CCUS 全流程系统进行投资成本预算是项目决策至关重要的步骤。CCUS 全流程系统包括3 个子工艺部分：CO2捕集、CO2输送、CO2驱油与封存。现有研究侧重于对CCUS 技术各子环节单独研究，缺少从系统角度的优化设计，Herzog[7]运用成本分解法对整体煤气化联合循环发电系统、天然气联合循环电厂和粉煤电厂的CO2捕集成本进行了详尽的分析和总结；Heddle[8]等对CO2的管道运输和封存成本进行了分析；梁大鹏[9]等对CCUS 全流程中CO2压缩、运输及封存环节的技术经济模型进行了总结，并着重分析了运输成本与输送距离、输送量之间的关系。经上述分析可知，从全流程角度对整个系统进行优化分析还处在起步阶段[9-12]。现有文献在对CCUS 全流程系统或子系统进行优化设计时，多对系统中不确定参数（如CO2的密度、CO2的黏度、电价和煤价等）波动所产生的影响忽略不计，在实际生产中，CCUS 系统中参数的波动会造成系统的能量损失和经济损失增大，甚至可能不满足实际工程要求。为了消除参数波动带来的不确定性对全流程系统造成的影响，本文采用鲁棒优化的方法建立CCUS 全流程系统的优化模型，将参数波动带来的不确定性影响加在约束条件中，进而通过改进的遗传算法求得系统的鲁棒最优解，最后与工程实例相对比，证明了该优化方法的优良性能。

2 优化问题描述及求解

2.1 优化方法

鲁棒优化是一种与计算工具相结合的建模方法，用于处理具有数据不确定性并且不确定性属于某个不确定集的优化问题[13]。遗传算法是通过模拟自然进化过程来搜索问题最优解的计算方法，它是从代表问题可能潜在的解集的一个种群开始的。采用遗传算法求解鲁棒优化模型的过程中，除了决策变量和目标函数值之外不进行其余任何数据交换，使求解过程中不确定参数的处理被大大简化，这个突出的优点使得遗传算法非常适合求解鲁棒优化问题[13]。

传统的遗传算法存在过早收敛和容易陷入局部最优值等问题，遗传算法中的三个基本遗传算子（选择算子、交叉算子和变异算子）参数的选取将对算法的性能和搜索速度产生直接的影响。因此，如何选择合适的遗传算子是算法能否高效收敛到全局最优解的关键。下文将对三种遗传算子进行改进，使用改进后的遗传算子可以加强算法的性能，跳出收敛较早和容易陷入局部最优解的困境。

2.1.1 选择算子的改进

选择操作是遗传算法中最基本的操作之一，选择算子的具体作用是以个体的适应度值为指标，从群体中选择优胜的个体，淘汰劣质个体。在进化的初始阶段，适应度较高的个体被选中的几率十分大，从而会产生相当数量的子代，容易导致种群的多样性缺失；在进化的末阶段，每个个体的适应度值已差别不大，该选择方法无法分辨个体的好坏，进而无法继续选择功能。本文对选择算子进行改进的步骤如下：

首先计算种群中每个个体的适应度值f和种群中个体的平均适应度值favg；其次，将每个个体的适应度值与平均适应度值进行比较，若个体的适应度值f≥favg，则进行选择操作，保留个体进入下一代；若个体的适应度值f＜favg，则计算按序排列的后50%个体的平均适应度值f0.5avg，若个体的适应度值f≥f0.5avg，则进行选择操作保留个体，不满足则直接淘汰。

采用该改进方法可以直接把适应度极小的个体淘汰，提升算法的收敛速度；亦能保证种群中优秀个体不被破坏，并且继续向着最优解的方向搜索[14-15]。

2.1.2 交叉算子的改进

交叉算子是遗传算法中起核心作用的遗传操作。传统的交叉操作是对于一对需要进行交叉操作的父代个体，以一个恒定不变的交叉概率来对这对父代个体实行交叉互换。该方法不考虑所需交叉父代个体的相似度，因而带有一定盲目性，有可能破坏父代个体的优良基因，造成算法收敛速度变慢或是不收敛。

本文引进相似度的概念来对交叉算子进行改进，具体操作步骤如下：

首先对两个父代个体Z 和W，计算其相似度S和交叉临界值r：

式中：C为个体Z和W共同最长子串的长度，R为种群中个体染色体编码的长度；g为当前的进化代数；G为总的进化代数。

比较该相似度S与交叉临界值r[14-15]：若S≥r，则不进行交叉操作，避免破坏父代的优良基因；若S ＜r，则以交叉概率Pc0进行交叉操作。

式中：Pcb为初始交叉概率；Pmin1为最小交叉概率。

从式（2）可以看出，该临界值是不断变化的，在进化操作的初期，个体被选中进行交叉操作的概率较大，可以增强种群的多样性；随着遗传操作进行至末期，个体被选中进行交叉操作的概率较小，进而可以保证优良个体不被破坏，延缓收敛进程。

2.1.3 变异算子的改进

变异算子的基本内容是对群体中的个体串的某些基因座上的基因值作变动，遗传算法中的变异概率通常是一个固定不变的常数。然而，随着进化的进行，种群中个体间的适应度值逐渐接近，变异概率将起不到优选的作用，使得整个进化过程没有竞争性，进化速度降低，甚至产生局部收敛的情况，对算法的性能产生极大的影响。本文对变异算子的选取进行改进，使其随着进化的进程自动调整具体数值，具体计算方式如下：

式中：Pmo为当前的变异概率；Pmax为变异概率的最大值（取0.3）；Pmin2为变异概率的最小值（取0.001）；fmax为种群中个体最大适应度值。

2.2 优化模型

2.2.1 决策变量及目标函数

含有不确定数据的鲁棒优化模型的一般形式如下[16]：

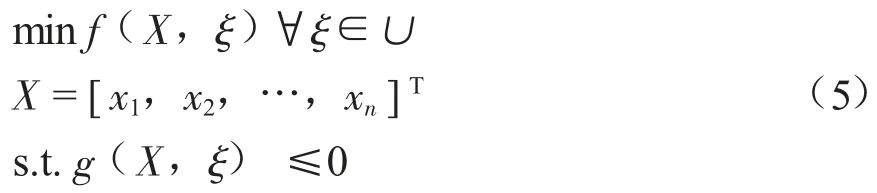
式中：X为优化问题的决策变量，ξ 为M维不确定参数集，g（X，ξ）为约束函数。

本文对待优化CCUS 全流程问题，以全流程系统总成本作为目标函数，寻求全流程系统中参数的最优配置。CCUS 全流程系统的优化模型由目标函数、决策变量和约束条件构成，并且包括诸如CO2的密度、温度以及电价、煤价等不确定参数，这些不确定参数的波动均在某个范围内。为了处理不确定性对全流程优化问题产生的影响，通过鲁棒优化的方法建立系统的优化模型，将不确定性转变为约束函数，进而将不确定性问题转化为确定性问题，采用遗传算法对优化模型进行求解。将一般优化模型式（5）中的目标函数转化为[17-20]：

式中：x1，x2，…，xn为全流程系统的决策变量，如CO2流量、管道入口压力、泵站数量和注入井口压力等；ξ1，ξ2，…，ξn为全流程系统中的不确定性参数，如CO2的密度、温度以及电价、煤价等。

2.2.2 约束条件

在实际CCUS 全流程项目运行中，需要满足流速约束、压力约束、储存约束、质量守恒等约束条件，为了便于计算，本文所选取的约束函数如下[17-21]。

2.2.2.1 质量平衡约束

CCUS 全流程系统中各子环节中CO2的质量应遵循质量平衡约束：从CO2排放源捕集的CO2量应不小于所运输的CO2总量，对于CO2驱油与封存环节CO2的封存量应不大于其运输CO2总量和回收回注CO2量之和。因此，CCUS 全流程系统中的质量平衡约束为：

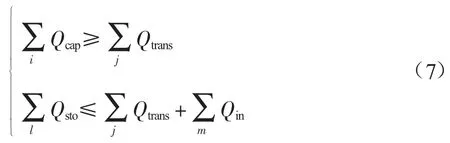
2.2.2.2 流速约束

在CCUS 全流程系统中，需对CO2的流速有所限制，若CO2流速过大，会使得全流程各子系统内设备压力增大，对设备造成损坏；若CO2流速过低，会导致CO2输送驱油与封存子环节时介质压力过低，需要额外增压才可以保障后续子环节顺利实施，降低了全流程系统的经济性。因此，CCUS 全流程系统中CO2的流速应满足：

式中：vmin、v、vmax分别为CO2最小、实际、最大流速，m/s。

2.2.2.3 压力约束

在CO2管输子系统中，需对管道内压力有所限制，输送管道由于受地形和管道自身等因素的影响，管道沿线的压力时刻在发生变化。为了使自捕集系统的CO2压力达到管输系统输送要求，需通过泵站加压使其达到管道最小运行压力，即管道内压力需不小于管道最小的运行压力且不大于管道所能承受的最大压力，同时管道出口压力应大于驱油与封存地点的最小注入压力：

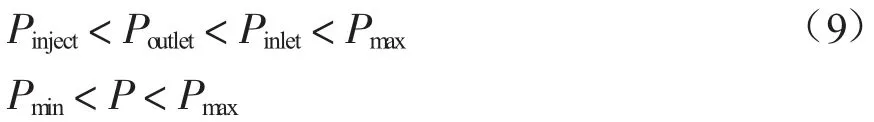
式中：Pinject为注入井口压力，MPa；Poutlet、Pinlet分别为管道出口、入口压力，MPa；、Pmax、Pmin分别为管道所能承受最大、最小运行压力，MPa；P为管道内实际运行压力，MPa。

CCUS 全流程系统优化模型根据式（5）可转化为：

对式（10）采用改进的遗传算法进行求解。

3 案例分析

由于CCUS 全流程模型中参数存在不确定波动，一般的优化方法无法解决该不确定性问题。本文将鲁棒优化方法和遗传算法结合起来，提出一种基于鲁棒优化的改进的遗传算法，算法流程如图1所示，其中ρave为CO2的平均密度，Call为系统总费用。

图1 CCUS全流程系统优化设计流程

本文对某燃煤电厂烟气CO2捕集纯化与驱油封存示范工程的经济性进行案例研究。假定CO2捕集率在80%以上；CO2采取管道运输方式，且运输的CO2相态为超临界；假定油藏深度为2000m；CO2的驱油比为 4t（ CO2）∶1t（ oil），即每注入封存4tCO2，可以增产原油1t；电厂单位造价根据中国电力工程造价信息网给出的计价规范进行预估；项目运行期为20 年。本文以CCUS 全流程系统总成本为目标函数进行优化，分析决策变量对目标函数的影响规律，进而验证优化方法的合理性。CO2流量、管道入口压力对全流程系统总成本的影响如图2 所示；CO2流量、注入井入口压力对全流程系统总成本的影响如图3 所示。

由图2 可得：在管道入口压力保持不变的情况下，随着CO2流量的增大，CCUS 总成本也随之增大；在CO2流量保持不变情况下，随着管道入口压力的增大，CCUS 总成本呈降低趋势；当管道入口压力大于11.5MPa 后，管道入口压力的增加几乎不再对全流程的成本产生明显影响，由此可得，若要提高CCUS 项目的经济性，应在满足工程要求的前提下，使得CO2的流量尽可能小并且管道入口压力较大。

由图3 可以看出：在CO2流量为定值的情况下，随着注入井口压力的增大，CCUS 总成本也随之增大；由于注入井的数量不得为0，计算得注入井口压力不得低于12MPa；在注入井口压力在12～15.6MPa 区间时，注入井口压力的增加对CCUS 总成本的变化几乎不产生影响；当注入井口压力大于15.6MPa 后，CCUS 总成本随注入井口压力的增大快速增长。