行星减速器动态特性的响应面近似建模方法研究

杨正龙，陈 娟，康 洪，杨 为

（1.中国北方车辆研究所车辆传动重点实验室，北京 100072；2.重庆大学 机械传动国家重点实验室，重庆 400044）

0 引言

多级行星传动系统具有多自由度、多间隙等特点，在啮合过程时齿轮副的弹性变形、时变啮合刚度和制造误差等都会对齿轮动态系统产生很大影响，影响了行星减速器在运转过程中的平稳性、安全性[1]。因此，行星减速器动态特性研究引起了国内外学者的广泛关注。李润芳[2]等运用有限元的方法建立了齿轮系的动力学仿真模型，通过对比实验和仿真结果来研究内部激励下的传动系统动态特性；刘文吉[3]等采用有限元法建立了渐开线少齿差模型，分析了动态齿轮的接触特性，得到了完整啮合周期的齿面接触应力、齿面滑动位移等啮合特性参数。

响应面法以多项式超曲面近似描述个变量之间的关系[4,5]，形式简单、计算方便，因此本文提出了基于响应面法建立行星减速器的动力学模型，以行星减速器的特征参数作为变量，以减速器表面的最大加速度为目标函数，建立了行星减速器动力学特性与特征参数之间的关系，有助于深入研究行星减速器的动力学特性。

1 试验水平和试验指标

某多级行星减速器主要由太阳轮、行星轮、齿圈、行星架以及箱体组成，其有限元模型如图1所示。在运转过程中，为了提高其承载力以及使用寿命，通常将太阳轮、行星轮、内齿圈进行正角度变位，这将避免跟切，减少齿面磨损，且能消除不变位的太阳轮与行星轮及内齿轮之间啮合的同心条件限制，综合考虑目标函数和约束条件的要求，选取太阳轮齿数zs，行星轮齿数zp，内齿圈齿数zr，太阳轮变位系数xs，行星轮变位系数xp，内齿圈变位系数xr，模数m和齿宽b。故此8个设计变量可表示为：

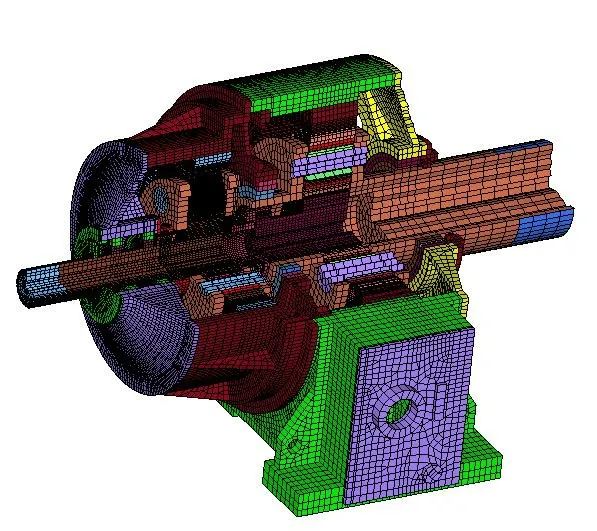
图1 行星减速器有限元模型

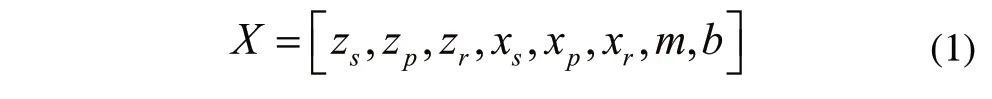
行星轮系不等角变位的方法是在太阳轮和内齿圈的齿数不变，而将行星轮的齿数减少1～2的情况下实现的。对于不变位或高变位行星轮系中各齿轮齿数的关系为：zp=（zr-zs）/2，而传动比和装配条件又只与太阳轮和内齿圈的齿数有关。因此，可以在满足传动比和装配条件的情况下，先确定zr和zs，然后按不变位的情况确定zp，再将减少1～2个齿数，若传动比保持不变，则齿数仅有一个是独立的，变位系数中仅有两个是独立的，此时的设计变量为：

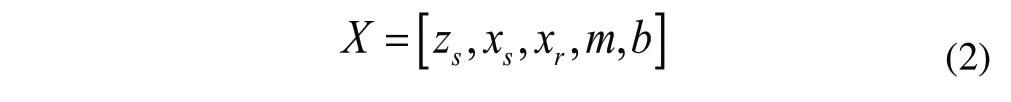
本文研究中试验设计工况为：输入转矩为4354.8N·m，输入转速为996.4rpm，功率为454Kw。结合研究对象和研究目的，分别将传动系统的最大应力和加速度作为试验的两个指标；进行试验时，需指定试验因素的取值范围，即可行的试验空间。对于行星齿轮传动，将传动系统齿轮参数的变化范围作为试验空间。表1为本次试验的试验空间。

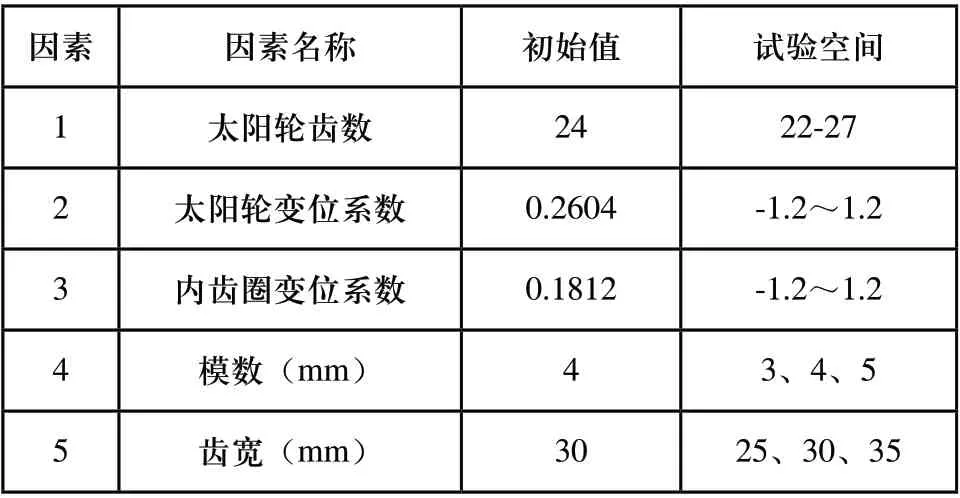
表1 试验因素及试验空间

表2 U30×（3013）均匀表及使用表

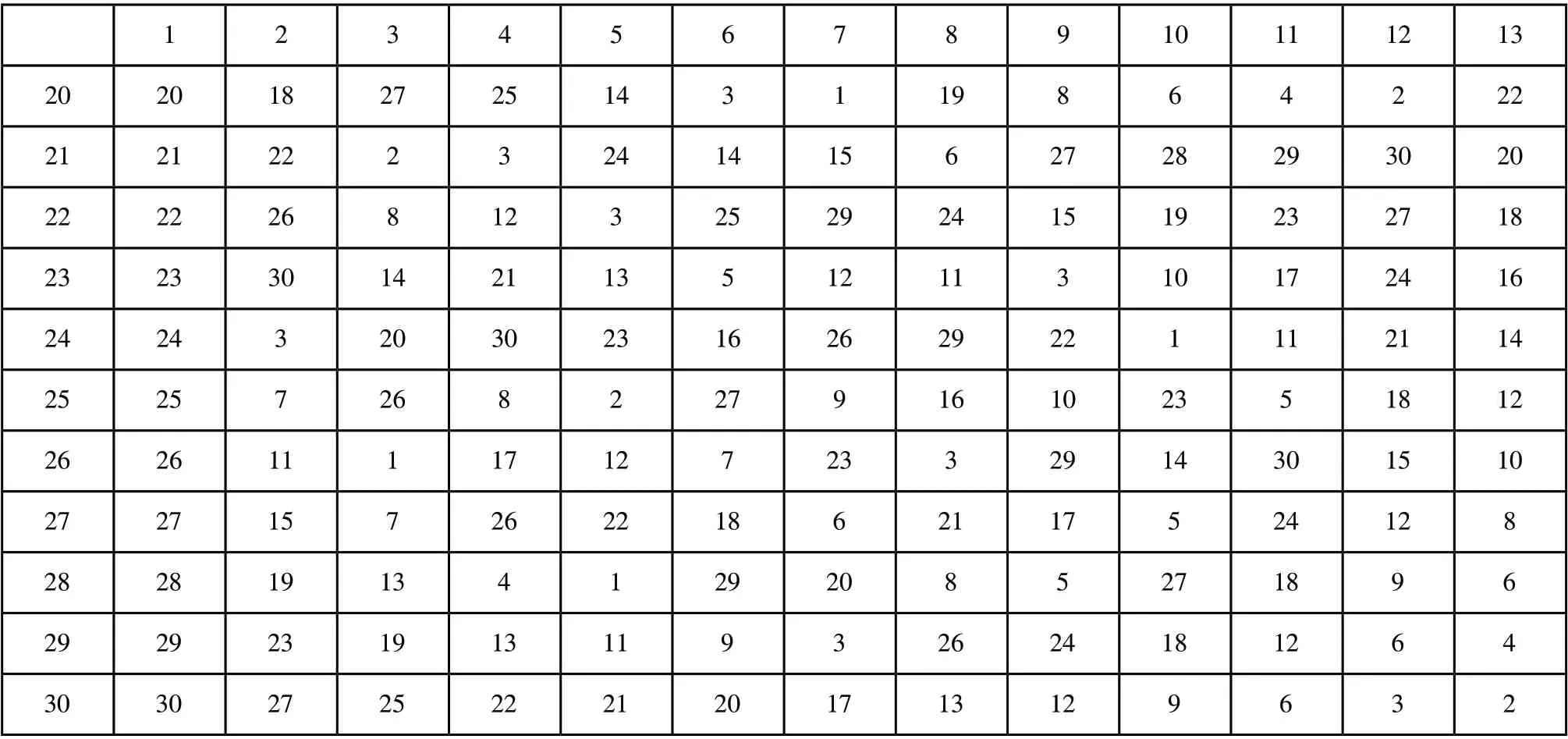
表2（续）

研究中涉及的试验因素有5个，根据均匀设计表，能安排5因素的试验方案有很多种。在均匀试验中，试验次数可以等于最大水平数，而试验次数与试验因数个数有关，一般来说，试验次数选为试验因素个数的3倍左右为宜，有利于建模和优化[6]。在本试验中，考虑到每个因素的取值范围较大，适当地增加试验次数有助于保证试验的精确性及提高响应面精度。

根据表2中的试验空间可知，本次试验各试验因素水平不同，故需采用混合均匀实验设计表，项目研究中在30水平的均匀表的基础上，将其变为五因素混合设计表。30水平的均匀设计表有U30×（3013）及其使用表如表2所示[7,8]。五因素试验的均匀度偏差为0.1465，试验时应按照均匀设计表中的第1、2、5、7和8列进行试验设计。

表3 U30×（3013）的使用表

建立的试验设计方案如表4所示。

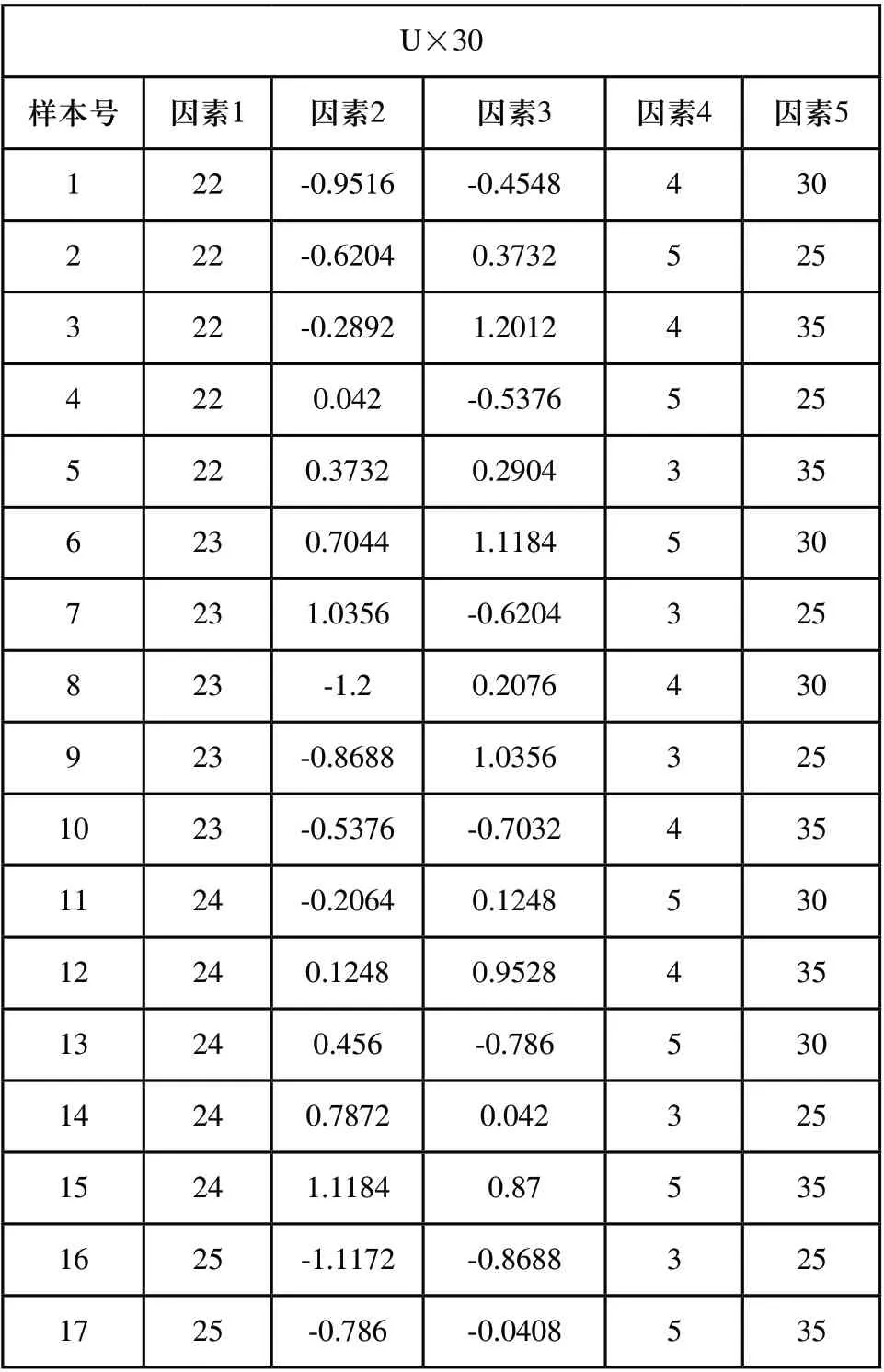
表4 试验设计方案

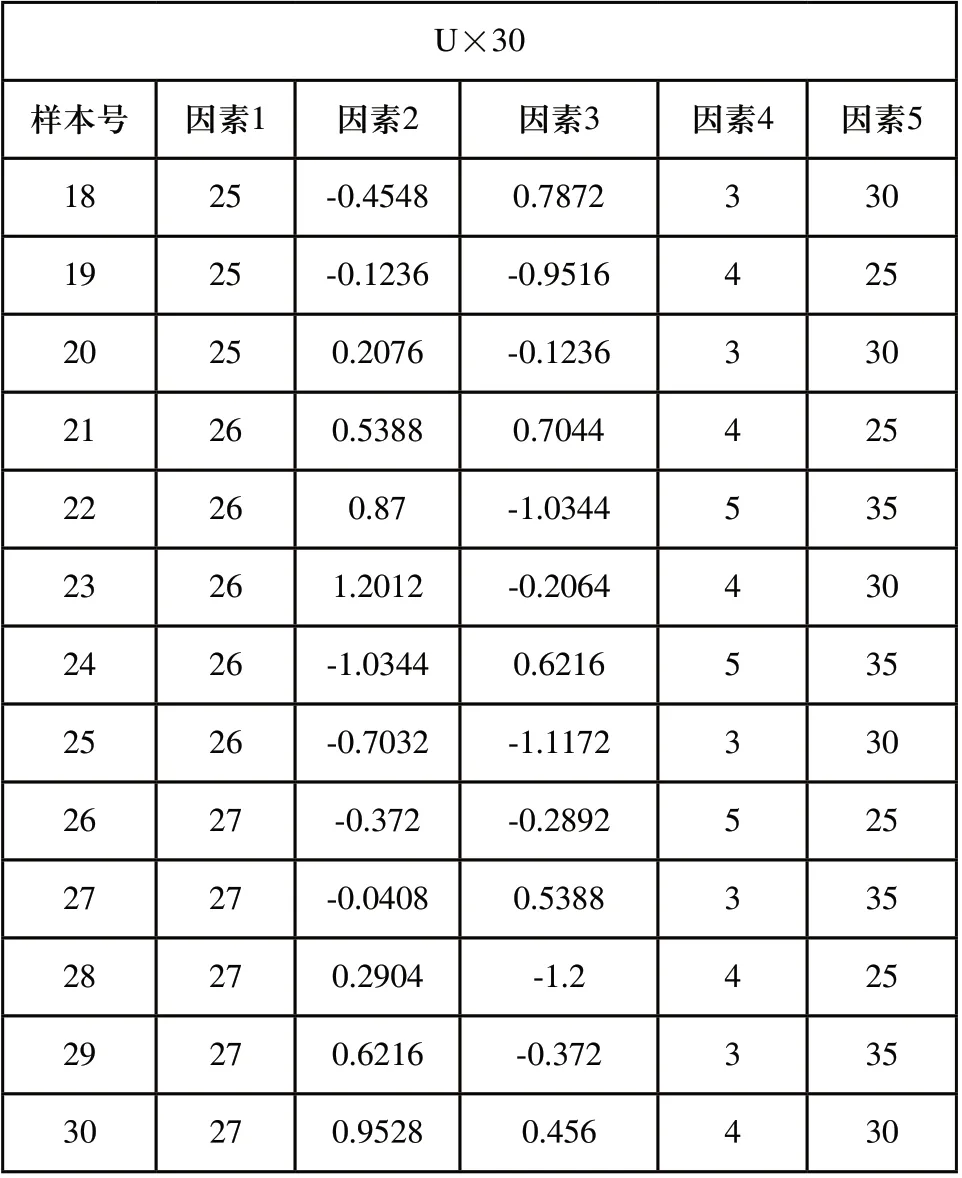
表4（续）

2 响应面模型

对设计变量和动态特性响应采用最小二乘法拟合，得到传动系统动态特性中表面最大应力Ystr和加速度Ya的二次多项式响应面近似模型，响应面拟合系数如表5和表6所示。

表5 传动系统表面最大应力响应面拟合系数

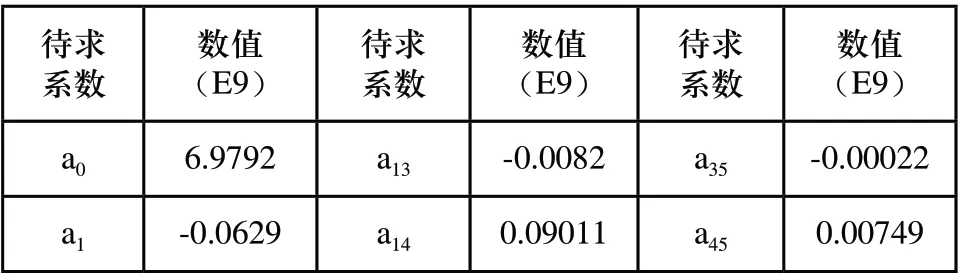
表6 传动系统表面最大加速度响应面拟合系数

表6（续）

3 近似响应面模型结果分析

1）误差分析

为了进一步判断响应面近似模型对真实响应面的逼近程度，需对拟合的二次响应面近似模型进行精确度检验。复相关系数R2和修正复相关系数R2adj常作为响应面模型精度的评价指标[9～11]，它们的计算结果如表7所示。两个响应面近似模型的复相关系数和修正复相关系数都大于0.9，满足工程精度要求，拟合得到的近似响应面模型精确可靠。

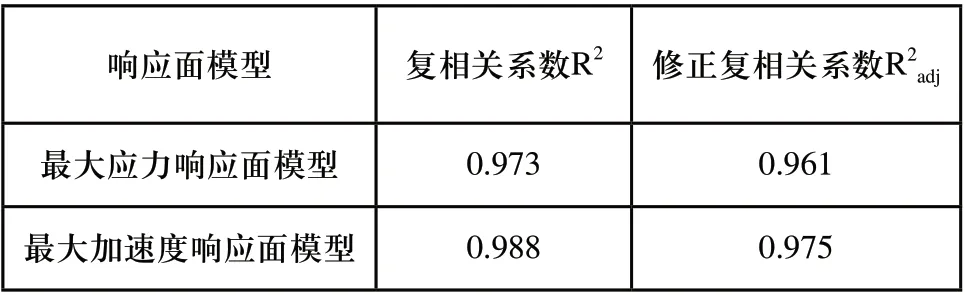
表7 响应面近似模型的复相关系数和修正复相关系数

2）结果分析及讨论

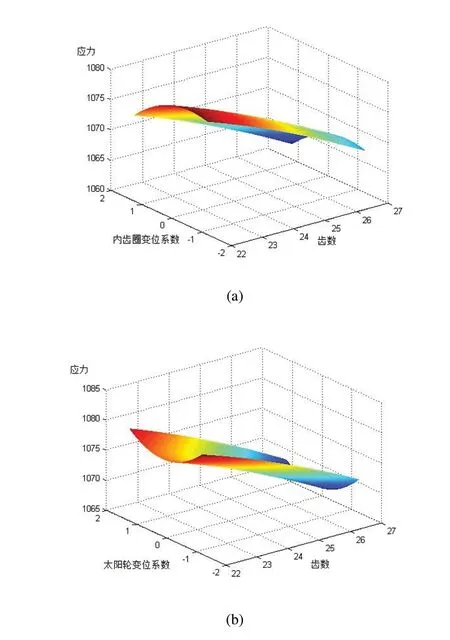
图2 基于系统应力的二次响应面交互项曲面

如图2所示，太阳轮齿数和太阳轮变位系数的交互项曲面为一个凸曲面，在一定范围内，当太阳轮齿数不变时，极限应力随着内齿圈变位系数的增大先增大后减小；太阳轮齿数和内齿圈变位系数的交互项曲面为一个凹曲面，极限应力随着太阳轮变位系数的增大先减小后增大；极限应力随着齿轮模数和齿宽的增大而减小，且模数和齿宽与太阳轮齿数的交互作用对系统应力影响较大。

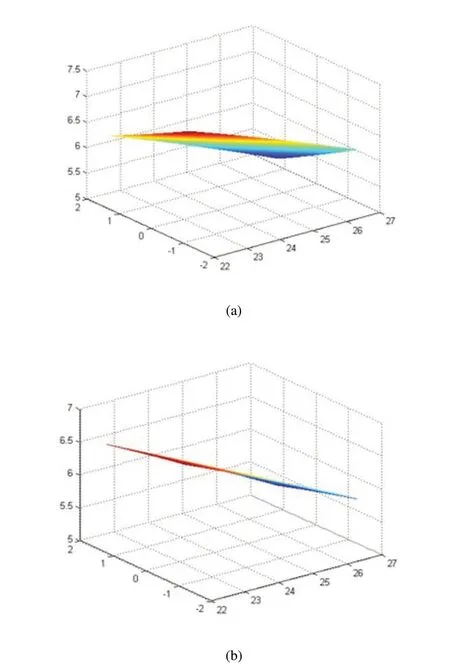
图3 基于系统加速度的二次响应面交互项曲面

如图3所示，太阳轮变位系数和内齿圈变位系数不变时，太阳轮齿数在较大值处系统加速度响应较小。模数和太阳轮齿数的交互作用以及齿宽和太阳轮齿数的交互作用对系统加速度响应影响较大，且在二者较大值附近，系统加速度响应最优。

4 结论

建立了减速器传动系统和箱体表面最大应力和最大加速度的二次多项式响应面近似模型，得到了行星传动系统特征参数与系统动态特性间的映射关系，得到的主要结论有：

1）当太阳轮齿数不变时，极限应力随着内齿圈变位系数的增大先增大后减小；太阳轮齿数和内齿圈变位系数的交互项曲面为一个凹曲面，极限应力随着太阳轮变位系数的增大先减小后增大；极限应力随着齿轮模数和齿宽的增大而减小，且模数和齿宽与太阳轮齿数的交互作用对系统应力影响较大。

2）太阳轮变位系数和内齿圈变位系数不变时，太阳轮齿数在较大值处系统加速度响应较小。模数和太阳轮齿数的交互作用以及齿宽和太阳轮齿数的交互作用对系统加速度响应影响较大，且在二者较大值附近，系统加速度响应最优。