新构型倾转旋翼无人机飞行力学建模

张练，孙凯军，叶川，崔凌博

(中国航天空气动力技术研究院 彩虹无人机科技有限公司，北京 100074)

0 引 言

倾转旋翼机是一种既具有常规直升机垂直起降、空中悬停能力，又具有螺旋桨飞机高速巡航能力的旋翼飞行器。倾转旋翼无人机对跑道没有要求，可在山区、岛礁、舰船等起降，在物流运输、监视、侦察等领域具有广阔的应用前景。无人倾转旋翼机可通过增加展弦比的方式提高航时，达到长时间运输或侦察的目的。

相比有人倾转旋翼机，无人倾转旋翼机发展起步晚、进展慢。美国和韩国相继研制了“鹰眼”和Smart UAV倾转旋翼无人机[1]。而国内仅做了一些小型的电动倾转旋翼无人机技术验证，还没有相关产品。

美国从20世纪50年代开始先后研制了XV-3、XV-15、V-22等倾转旋翼机。20世纪80年代，S.W.Ferguson[2-3]对XV-15倾转旋翼机进行了大量风洞试验并形成了著名的GTRS模型报告。国内外对倾转旋翼机飞行力学的研究大多以XV-15为建模对象[4-5]，沙虹伟[5]和Song Yangguo等[6]对小型倾转旋翼无人机进行了建模和飞控研究，但是由于他们研究的仅是十几千克的小型电动倾转旋翼无人机，难以完全验证模型的准确性；曹芸芸[7]在XV-15模型的基础上，分析了倾转旋翼机倾转过渡走廊、旋翼与机翼的气动干扰，但是XV-15模型采用了大量基于实际飞行和风洞试验得到的经验数据和公式，这些经验数据和公式不适用于新研的倾转旋翼机。

倾转旋翼机飞行力学模型一般采用分体建模方法，同时考虑各个部件之间的相互干扰，主要表现在旋翼与机翼的干扰[8]。旋翼模型最复杂的部分是旋翼入流模型和挥舞运动模型。理论和试验证明Pitt-Peters动态流入模型能满足工程应用[9-10]。目前大部分相关文献中给出的挥舞运动方程都是经过简化后得到的计算公式[11-12]，这种计算方式采用了大量的假设，对弦长和扭转角随展向位置非线性变化的桨叶并不适用。

本文针对一款在研的新构型倾转旋翼无人机进行配平及稳定性分析。旋翼模型采用叶素理论并参考CFD和缩比桨叶试验数据进行修正；将求解挥舞角度理解为求微分方程，采用数值方法进行迭代求解，这种求解方式可以适用于任意形状的桨叶。

1 新构型倾转旋翼无人机

新构型倾转旋翼无人机的研制初衷是设计一款满足垂直起降和长时间飞行的无人机。垂直起降无人机根据技术路线的不同，分为复合翼、直升机、尾坐式无人机、倾转旋翼机等。复合翼构型简单，技术成熟，垂直起降状态类似于多旋翼，但是起飞质量难以做大，并且难以长时间悬停作业。直升机具有长时间空中悬停功能，但是飞行效率低，航时短。尾坐式无人机起降状态操作性较差，在模态转换过程中机翼容易失速，转换走廊范围较窄。倾转旋翼机通过倾转旋翼实现直升机和固定翼的过渡，可以适当降低飞行速度，提高巡航升阻比以实现长航时飞行。

倾转旋翼机为减小垂直起降状态机翼翼根弯矩，提高机翼刚度，避免发生结构动力学问题，机翼展弦比一般较小，例如，V-22“鱼鹰”倾转旋翼机机翼展弦比为7，韩国小型倾转旋翼机展弦比为6。机翼展弦比对固定翼巡航状态的升阻比影响很大，常规倾转旋翼机较小的机翼展弦比导致其固定翼巡航状态升阻比较低，严重制约了航时、航程等性能指标。

为了提高倾转旋翼机展弦比，机翼设计成内外两段机翼，外翼段随旋翼一起倾转。内侧机翼的展弦比为6，整个机翼展弦比为10。垂直起降外形图如图1所示。

图1 新构型无人倾转旋翼机Fig.1 New configuration tilt-rotor aircraft

新构型无人倾转旋翼机基本参数如表1所示，该无人机相比常规倾转旋翼无人机或者直升机，续航时间明显变长。

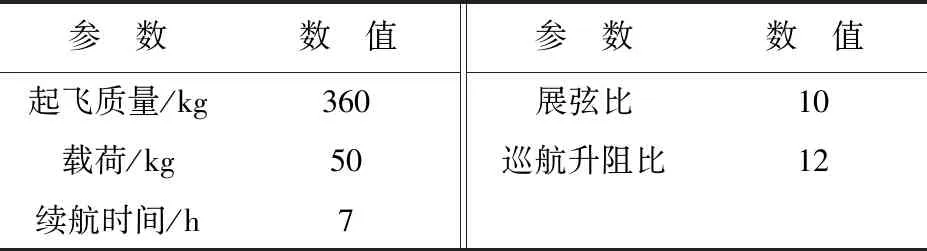
表1 新构型无人倾转旋翼机基本参数Table 1 Basic parameters of new configuration tilt-rotor aircraft

2 飞行力学模型

倾转旋翼机飞行力学模型在数学上表现为强非线性，无法通过显式方程进行表达和求解[13]。其中最为复杂的为旋翼部分，相比直升机，倾转旋翼机桨叶形状和翼型更为复杂，气动力无法通过简化的积分公式来表示。机翼模型分为内外两段分别进行建模[14]。其他部件力学模型与常规固定翼飞机类似。

2.1 旋翼建模

2.1.1 叶素理论

倾转旋翼无人机有左右两个旋翼，从上往下看，左旋翼顺时针旋转，右旋翼逆时针旋转，以右旋翼为例，建立叶素理论模型。

右旋翼叶素在惯性坐标系下位置矢量为

r=rH+rs

(1)

式中：rH为旋转中心位置矢量；rs为叶素相对旋转中心位置矢量。

惯性坐标系下速度矢量为

(2)

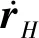
桨叶叶素速度在构造旋转坐标系下速度分量为

(3)

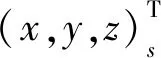
(4)

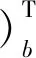
桨叶叶素在构造旋转坐标系中的坐标为

(5)

桨叶叶素在构造旋转坐标系中的速度坐标为

(6)

式中：β为挥舞角，挥舞角的计算流程在后文中给出；ψ为方位角。

叶素相对气流的切向速度UT，垂向速度UP，径向速度UR分别为

(7)

此处规定垂向速度UP当气流由上往下吹时为正。λ为叶素位置的诱导速度，λ在后文通过引入动态入流理论计算。

切向速度UT和垂向速度UP的合速度记为UB，则有

(8)

叶素剖面的攻角为

α=θr+θ0+θccosψ+θssinψ+β*

(9)

β*=-arctan(UP/UT)

(10)

式中：θr为桨叶安装角，根据桨叶几何形状通过插值获得；θ0为总距角；θc和θs分别为纵向和横向周期变距角；β*为来流角。

根据叶素剖面的攻角，通过插值得到翼型升力系数CL和阻力系数CD。

从而计算叶素的升力和阻力

(11)

叶素垂向力和切向力分别为

(12)

叶素切向力在构造旋转平面内，垂直于桨叶在构造旋转平面投影，垂向力在桨叶挥舞运动所在平面内，垂直与桨叶。

在构造旋转坐标系下，叶素拉力、后向力、侧向力分别为

(13)

叶素滚转力矩、俯仰力矩、扭矩分别为

(14)

挥舞力矩为

dMβ=r×dTscosβ

(15)

2.1.2 入流模型

描述直升机旋翼不同方位角和桨叶半径处入流大小，常用的入流模型为Pitt动态入流模型。假设入流速度为

λ=λ0+λsrsinψ+λcrcosψ

(16)

根据动态入流模型，在定常飞行状态，λ0,λs,λc可通过式(17)计算：

(17)

其中，

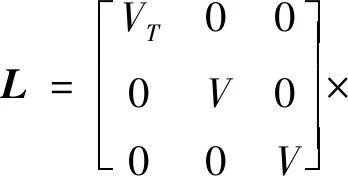
(18)

(19)

(20)

(21)

(22)

(23)

式中：u1,u3为来流在桨盘平面分量；u2为来流在垂直桨盘方向的分量；λm为均匀入流速度。

给定初始状态的拉力系数、滚转力矩系数、俯仰力矩系数，便可根据式(16)～式(23)迭代完成入流速度计算。

2.1.3 挥舞运动模型

新构型倾转旋翼机桨叶几何弦长和扭转角都是非线性变化的，无法通过简化公式求解挥舞运动。

计算挥舞角可以理解为求解常微分方程问题，采用数值迭代的方式计算不同方位的挥舞角，将旋转平面均匀分解为N块，则每块对应度数为

(24)

假如通过方位角n度的挥舞角能推算出第n+dpsi度方位角处挥舞角，则可进行迭代计算。

采用常微分方程数值解法中的Taylor展开法：

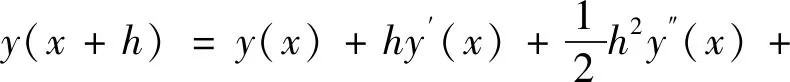
(25)

则有：

(26)

其中，

(27)

(28)

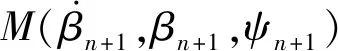
2.1.4 旋翼气动力计算流程

旋翼气动力计算需要进行内外层迭代，内层为挥舞运动收敛，外层为诱导速度收敛。计算流程如图2所示。

以5 m/s平行桨盘方向来流为例，计算得到第一个外循环下，挥舞运动收敛史以及整个计算过程中旋翼拉力收敛史，如图3～图4所示。

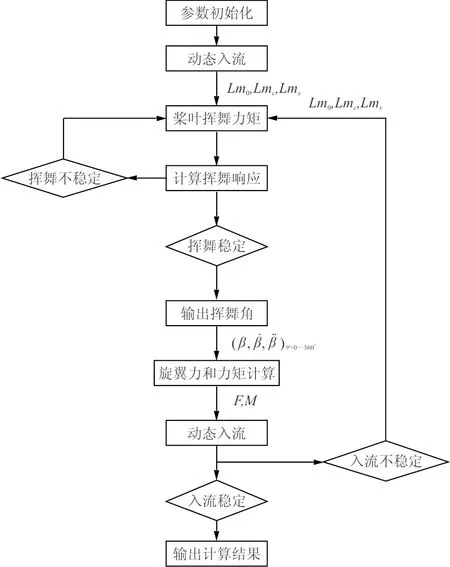
图2 旋翼气动力计算流程图Fig.2 Calculation flow chart of rotor aerodynamic

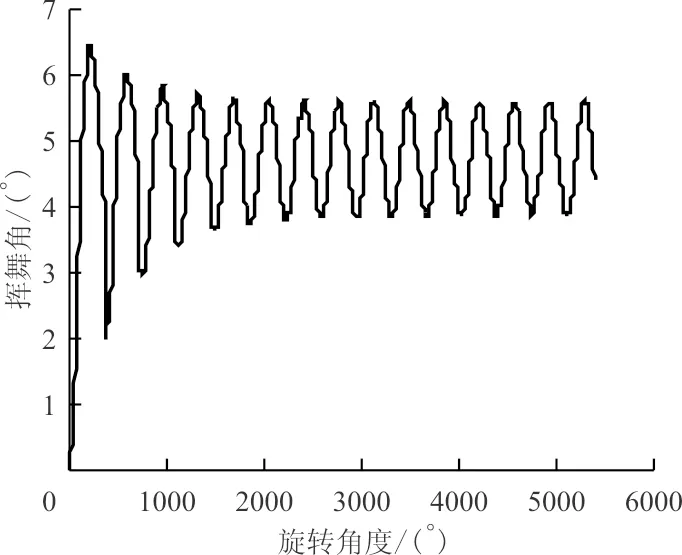
图3 内环迭代挥舞角收敛史Fig.3 Flapping angle convergence history of inner iteration

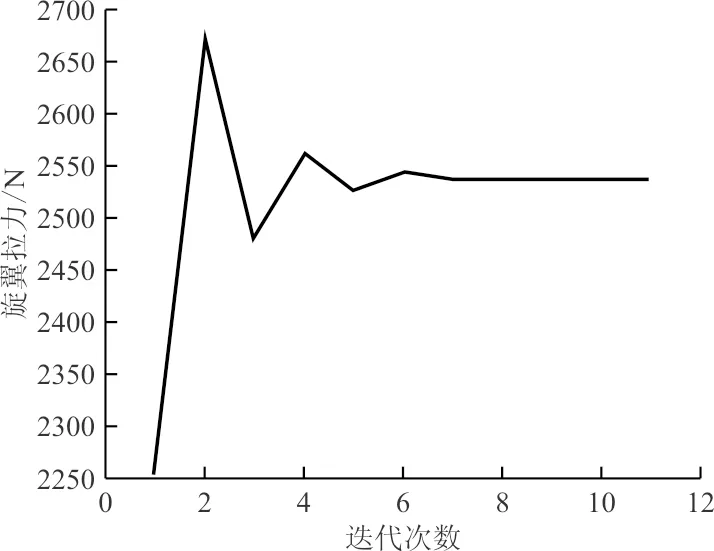
图4 外环迭代拉力收敛史Fig.4 Tension convergence history of external iteration

从图3可以看出：第一个外环迭代内，旋翼经过10圈迭代后，挥舞运动稳定，而随着外环迭代次数增多，旋翼挥舞稳定需要的迭代圈数会减小。

从图4可以看出：经过10个外环迭代，旋翼拉力收敛。

2.1.5 旋翼气动力计算结果

为了验证旋翼模型的准确性，对比分析CFD和商业软件计算结果。不同方法计算得到的旋翼拉力和扭矩随桨距角的变化曲线如图5～图6所示。

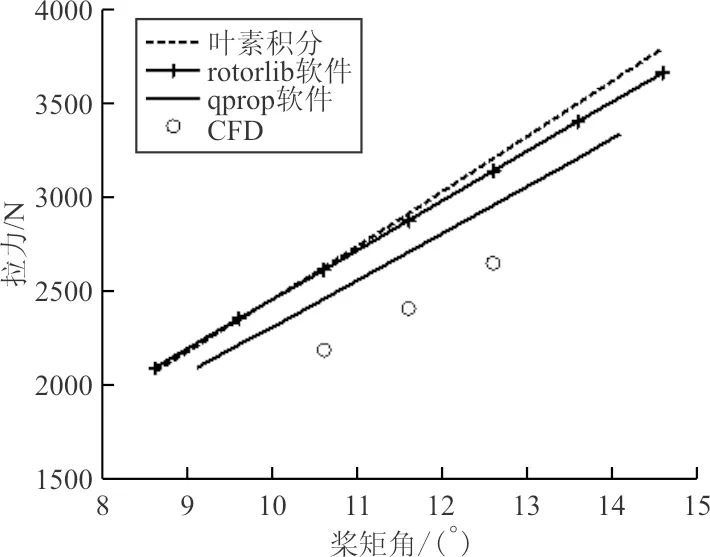
图5 旋翼拉力计算结果对比Fig.5 Comparison of rotor tension calculation results

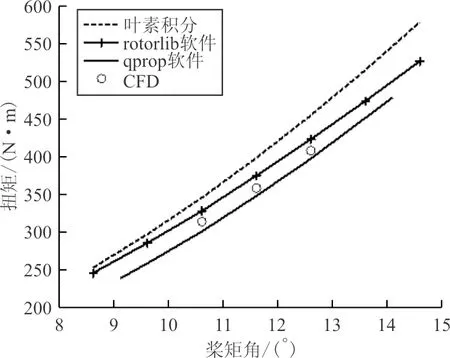
图6 旋翼扭矩计算结果对比Fig.6 Comparison of rotor torque calculation results

从图5～图6可以看出：四种方法计算得到的拉力和扭矩有一定偏差，但是斜率相近；CFD计算结果通过缩比试验验证了其准确性，进而间接验证了本文模型计算得到的气动力与真实情况气动力斜率相近。

2.2 内翼段模型

机翼在低速飞行时会受到旋翼尾流的影响，这种情况下将机翼分为受尾流影响的滑流区域和不受影响的自由流区域。机翼总气动力等于这两部分气动力相加。

滑流区的升力和阻力为

(29)

式中：qwi-h为滑流区动压；Swi-h为滑流区面积。

滑流区气流速度为

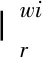
(30)

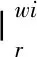
为了计算滑流区面积Swi-h，首先计算旋翼尾流在滑流区的影响半径，根据经验公式计算旋翼尾流半径[15]：

(31)

式中：R为旋翼半径；l为内翼段到旋翼旋转中心距离。

以旋转中心为圆点，Rw为半径得到的圆在机翼平面投影与机翼相交的面积，即为滑流区面积。

根据质量守恒计算旋翼尾流在内翼段滑流区的平均速度：

(32)

式中：v0为桨盘处诱导速度。

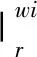
自由流区的升力、阻力、俯仰力矩为

(33)

式中：CLδf为单位襟副翼偏转对升力系数影响值；δf为襟副翼偏转角。

侧向力、滚转力矩lw、偏航力矩Nw通过CFD数据插值计算得到。

为了验证内翼段建模的准确性，将建模计算得到的升力与CFD计算得到的结果进行对比，如图7所示，可以看出：建模计算得到的数据与CFD计算结果吻合度较好，验证了内翼段建模方法的准确性。

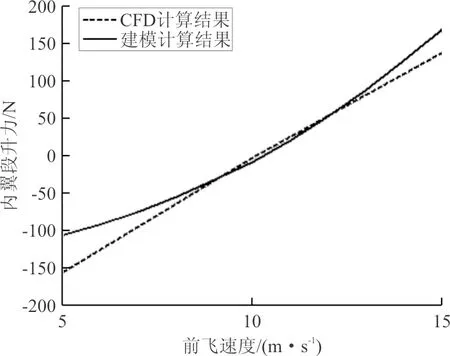
图7 内翼段升力计算结果对比Fig.7 Comparison of inside wing lift force calculation results

2.3 外翼段模型

外翼段是新构型倾转旋翼机特有的部件。外翼段主要受旋翼尾流和自由来流影响，并且外翼段随着旋翼一起倾转，不同倾转角度下，外翼段压心位置处的速度为

(34)

外翼段压心处攻角和侧滑角分别为

(35)

根据攻角和侧滑角进行二维插值计算气动力和力矩。

3 配平计算结果

所谓配平计算，就是求解无人机处于平衡状态时的状态量和操纵变量。对于常规直升机有纵横向周期变距、总距、尾桨矩四个操纵变量，而倾转旋翼机除了直升机的周期变距和总距操纵变量，还有固定翼飞机的舵面操纵量。直升机和固定翼操纵功效随着前飞速度和倾转角度变化[16]。

有人倾转旋翼机一般有四个操纵动作，飞控系统根据飞行速度和倾转角度自动分配操纵动作对应的操纵功效[17]。而无人机可以不限于四个操纵动作，使得倾转旋翼无人机飞行力学方程存在无穷组解。

为了简化计算和分析直升机模式配平状态总距和周期变距随着前飞速度的变化。将固定翼操纵量全部取零，直升机操纵方式保留总距和纵向周期变距，这样就存在四个操纵变量：右旋翼总距操纵、右旋翼纵向周期变距操纵、左旋翼总距操纵、左旋翼纵向周期变距操纵。

根据以上分析计算得到直升机模式不同前飞速度配平结果如图8～图10所示。

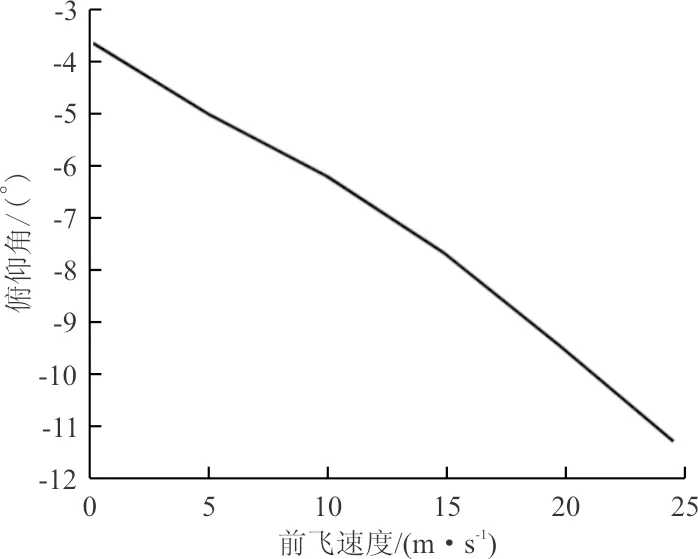
图8 俯仰角随前飞速度变化Fig.8 Pitch angle with respect to airspeed

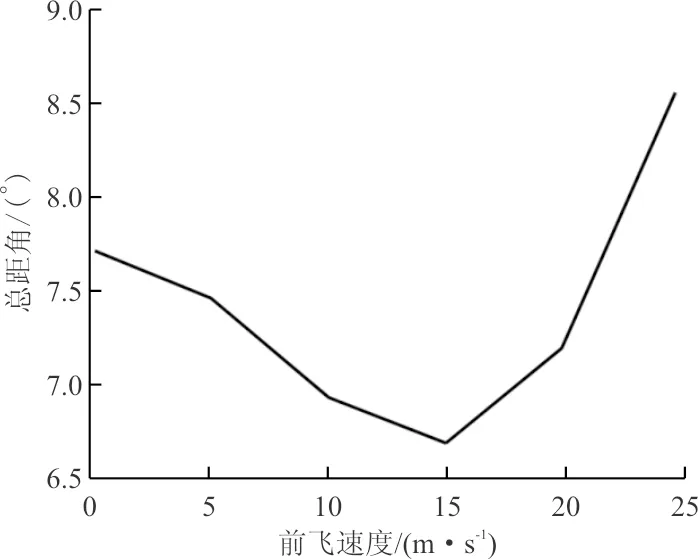
图9 总距角随前飞速度变化Fig.9 Collective pitch with respect to airspeed

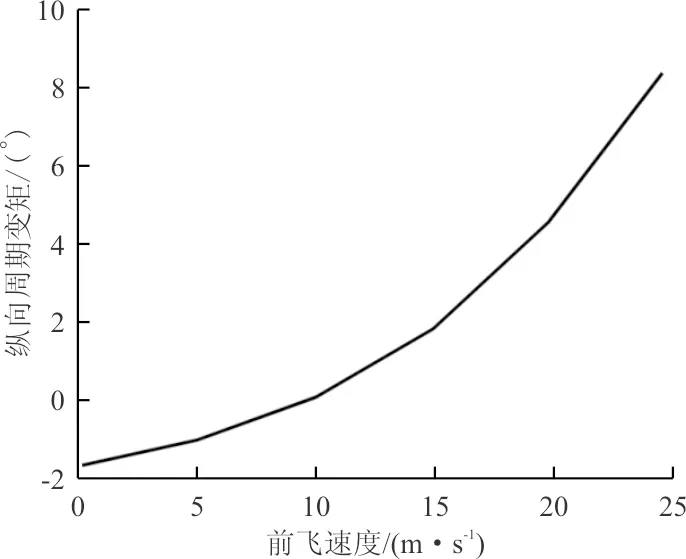
图10 纵向周期变距随前飞速度变化Fig.10 Longitudinal periodic variation with respect to airspeed

从图8～图10可以看出：随着前飞速度增大，机身俯仰角越来越小，机身有低头趋势；总距先减小后增大，这是由于随着前飞速度增大需用功率先减小后增大；纵向周期变距一直增大，表明桨盘前倾角越来越大。

倾转过渡状态配平与直升机状态配平类似，在特定倾转角下进行定常计算，不考虑动态过程。

4 稳定性分析

稳定性体现的是无人机保持原有运动姿态或者抵抗外界干扰的特性。采用小扰动假设，推导倾转旋翼无人机本体状态方程，进而得到特征根和特征矩阵。

求解状态矩阵有两种方法：一种是通过求运动方程偏导数得到数学表达式，再带入平衡点处数据计算得到状态矩阵；另一种方法是通过数值方式求解运动方程在平衡点处的Jacobian矩阵，此矩阵即为状态矩阵。由于第一种方法数学公式繁琐，本文采用第二种方法求解无人机本体状态矩阵。

以直升机模式悬停状态为例，计算得到状态方程：

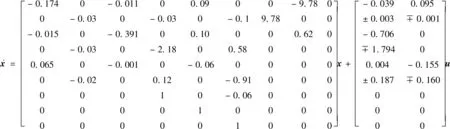
式中：x=[ΔuΔvΔwΔpΔqΔrΔφΔθΔψ]T，对应欧美坐标系下三个速度、角速度和欧拉角；u=[Δθ0r,lΔθsr,l]T为左右总距和左右纵向周期变距。

从状态矩阵可以看出，横纵向基本没有耦合。对于常规直升机旋翼，一个前向的速度增量会导致旋翼侧倒，产生一个侧向力增量，也就产生了横纵向的耦合。而倾转旋翼无人机左右旋翼旋转方向相反，左右旋翼由于前向速度增量产生的侧向力相互抵消，故纵向速度增量不会导致横向的状态改变，即横纵向基本没有耦合。

根据状态矩阵计算得到悬停状态的特征根，并与商业软件rotorlib计算得到的特征根进行对比，如表2所示。商业软件由于自身设定的限制，目前还无法定义外翼段，其计算结果与常规倾转旋翼机类似。

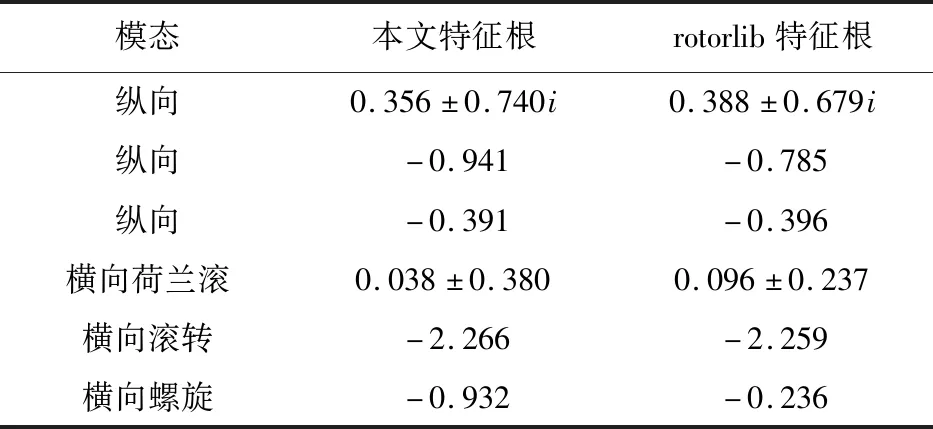
表2 特征根计算结果对比分析Table 2 Comparisons of calculation results of eigenvalues

从表 2可以看出：纵向计算结果两者接近，本文横向计算结果的螺旋模态和荷兰滚模态稳定性较好，即外翼段有利于对横航向稳定性。

基于本文模型，进一步计算得到直升机模式下不同前飞速度的特征根，如图11所示。

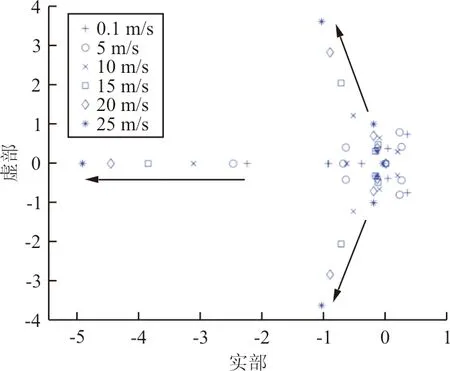
图11 特征根随前飞速度变化Fig.11 Eigenvalue movement with respect to airspeed

从图11可以看出：前飞速度增大，特征根实部有向左移趋势，稳定性增强。

5 结 论

(1)增加机翼外翼段能提高直升机模式横航向稳定性；倾转旋翼机直升机模式悬停状态由于左右旋翼转向相反，左右旋翼纵向变量产生的横向力相互抵消，横向变量产生的纵向力亦相互抵消，故横纵向基本没有耦合。

(2)新构型倾转旋翼无人机相比常规倾转旋翼无人机具有巡航效率高、航时长的优势。

(3)本文重点研究了直升机模式配平及稳定性分析，随着工程进展不断深入，下一步将研究无人倾转旋翼机过渡状态控制策略。