数学问题2336题的简解与推广

吕永军

(浙江省永康市第六中学 321300)

提出问题者刘才华老师在《数学通报》2017年第1期，利用三角函数进行证明，运算量较大.本文利用圆的定义与几何性质及平面解析几何方法，给出两个较简单的方法，并对此问题进行一些推广.

方法一连接OQ，ON，因为MN是过点Q的⊙O的切线，所以OQ⊥MN，

由已知可知OB⊥PB，所以N，B，O，Q四点共圆，

所以∠NBQ=∠NOQ，

而∠NOQ=∠NOB，

得∠PBC=∠NOB，OB=PB，

所以BN=PC.同理MA=PD，

又因为PA=PB，则DN=CM，

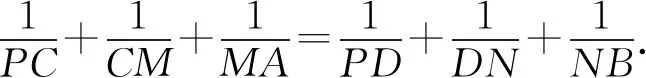
方法二圆中问题还可以通过建立直角坐标系，通过解析方法来解决.

所以OA⊥OB，建立如图所示坐标系，

设圆O的半径为r，

所以A(0,-r)，

B(-r,0)，P(-r,-r)，

设Q(rcosα,rsinα)，

则直线MN：xcosα+ysinα=r，

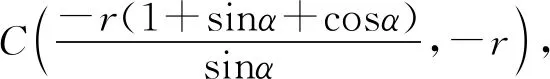
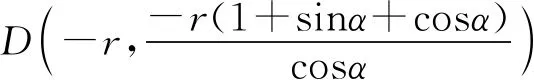
所以|NB|=|PC|，

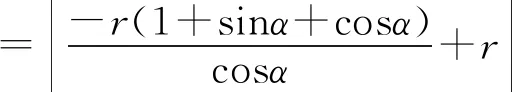
所以|PD|=|MA|，

所以|DN|=|CM|,

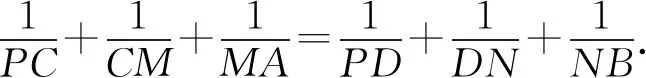
当然也可以用几何方法证明.

推广二：将问题中的圆改为椭圆，其它条件不变，结论是否仍成立呢？能否还可以得到其它结论？

则(1)|PC|·|MA|=|CM|·|PA|；

证明(1)P(-a,-b)，A(0,-b)，B(-a,0)，

设Q(acosα,bsinα)，

|PA|=a,

所以|PA|·|CM|=|PC|·|MA|.

(3) 由(2)可知成立.