如何正确解读假设检验结果——兼谈数学教育研究中p值误用问题

宋 爽 曹一鸣

(首都师范大学 100048) (北京师范大学 100875)

1 前言

随着教育研究的不断深入和教育研究国际化交流的推进，近年来国内也掀起了实证研究的热潮.2017年1月全国教育实证研究联席会议召开，号召加强教育实证研究、促进研究范式转型.实证研究越来越受到教育研究者的重视，实证研究中关于量化研究的统计方法和统计模型也备受青睐.相较于其他学科，数学教育研究者因为具备较好的数学与统计学基础知识，所以也更擅长且更愿意使用量化研究方法，如《数学通报》刊载喻平教授多篇文章指导量化研究方法的使用[1,2]，数学教育研究领域中量化研究的发展也更为快速.但迅猛增长的数学教育量化研究和统计方法使用的过程中仍暴露了一些问题，其中以假设检验的误用及p值的错误解读最为常见.一方面，数学教育研究者相较于其他学科的教育研究者尝试使用了更为复杂的统计模型和统计方法，增加了犯错的风险；另一方面，数学教育研究者过往的数学经验也在一定程度上影响了对统计推断的理解，将统计推断和演绎推理或概率推导产生了混淆.事实上，统计推断和概率推导看似名称接近，但实则两者逻辑基础差异极大[3].

近年来，不断有国际知名期刊及学术机构发表了对学术研究中p值报告的新要求[4,5]，甚至有权威期刊申明拒绝报告p值[6].这使得部分不明真相的研究者误以为p值甚至假设检验已经被废，“p值已死”成为热议话题，当然也不乏一些网络媒体为博人眼球刻意进行片面宣传.一些研究者对统计假设检验的基本含义、概念及科学规范的使用方法了解有限，很容易将这些期刊和机构的无奈之举误解为p值本身是错误的、无用的.因此，为了促进数学教育实证研究的规范化和科学性，对量化教育研究起到引领作用，有必要对权威学术期刊“拒绝”p值的原意进行解读，并说明做假设检验时应该注意的事项.

本文将在数学教育量化研究背景下探讨假设检验的内涵，为假设检验和p值的科学使用进行结合示例的讲解和直观的说明，解读权威机构和学术期刊拒绝报告p值背后的原因，揭示原始文献中p值提出者的本意和初衷，以及他们对后来研究者的告诫.通过有针对性的说明，本文力图引导数学教育研究工作者科学规范地使用假设检验、关注研究问题本身，而不要被统计显著性束缚住科研的脚步.

2 统计假设检验在数学教育量化研究中的含义

统计假设指的是对总体的某统计指标的假定性说明，通常将总体的统计指标称为参数(parameter)，而对应于总体参数的样本特征可以称之为统计量(statistic).在教育研究中，研究者希望了解的当然是事物总体的特征，或者说希望得到一个普遍适用的模型，例如某种教育方法的效果、不同个体特征学生的数学学业成就差异等.然而多数情况下，获得总体特征的愿望是个“不可能的任务”，因此用样本特征对总体特征进行估计、推断、猜测的“假设检验”方法应运而生.假设研究的问题是7年级学生在某个数学测试中的成绩是否存在性别差异，理论上应当让全世界所有7年级学生参加测试，再进行不同性别的比较，但这种操作费时费力且难以达成.多数研究者的做法是利用随机抽样的样本特征来对总体进行估计，常见的方式就是对样本数据进行t检验，而这种利用统计量对统计假设进行检验的过程，就是通常所说的假设检验，也可以将其称之为统计推断.

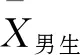
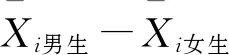
至此，应当进一步明确拒绝域的确定，以及拒绝域和p值的关系.拒绝域的范围取决于用于假设检验的统计量的分布和研究者所定义的显著性水平.以比较男女生数学测试成绩差异为例，为了对总体均值差异进行推断，通常对样本数据进行t检验，此时用于检验的统计量t值服从t分布，其自由度由样本个数决定.t分布是以0为中心左右对称的单峰分布，是t值与概率密度相对应的图像，其图像下方、横坐标上方所夹区域就是整体的累积分布频率，其值为1.如图1所示，在t分布概率密度函数图像中两条实线(同样关于纵坐标对称)所夹区域面积为0.95，而两侧对称的灰色区域面积之和占总面积的5%，因此两侧的区域就是双侧检验中显著性水平为0.05的拒绝域.与之类似，虚线右侧斜线阴影区域面积也为总面积的5%，因此该斜线阴影区域即为单侧检验中显著性水平为0.05的拒绝域.对于确定的自由度和显著性水平，拒绝域及其相应的临界t值是完全确定的，将假设检验中计算所得的t值与该临界值做比较就可以确定是否统计意义上“拒绝”或“接受”原假设.同理，研究结果中报告的p值就是根据计算所得t值和对应自由度的概率密度函数，对应出t值以外图像下的面积，该面积(单侧检验时)或该面积的两倍(双侧检验时)即为所报告的p值.将该报告的p值与显著性水平做比较，也同样可以确定是否统计意义上“拒绝”或“接受”原假设.以上两种逻辑都是常见的检验方式，除此之外还可以通过判断置信区间是否包含0值的方式来进行检验，而置信区间的确定也同样取决于样本统计量(和t值能够互相转化)、自由度、及所定义的显著性水平.

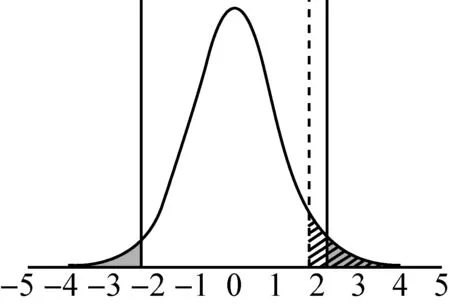
图1 假设检验原理示意图

3 数学教育研究中进行统计假设的过程及两类错误

针对前文所列的原假设和备择假设，假设对所有7年级学生进行了五次抽样，为具体说明假设检验的过程，在此利用MATLAB的normrnd命令模拟随机抽样，从三个不同分布的总体中分别各“抽样”5轮，每轮各获得“随机抽样”的数值5个作为样本数据(以下数据保留2位小数).三个总体分别为：总体男，均值为80，标准差为5的正态分布；总体女甲，均值为80，标准差为5的正态分布；总体女乙，均值为90，标准差为5的正态分布.显然，总体中μ男-μ女甲=0，μ男-μ女乙≠0.那么，当我们利用样本对总体进行估计时，是否一定能得到和真实情况一致的推断呢？

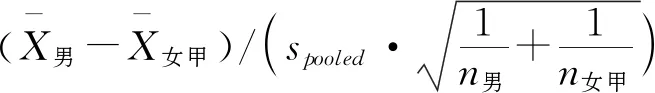
接下来可以构造出另一个样本的数据，即样本A，该样本中的所有数据都来源于样本1至样本5中的数据，但有意选择了男生成绩中较大的数据和女生(甲)成绩中较小的数据.由于所有模拟数据都是随机生成的，我们当然有可能在两正态分布总体中通过随机抽样中获得类似样本A这样的样本.在该样本中可以发现，t值为8.500，p值达到了0.000028.按照假设检验的逻辑和做法，此处应该“拒绝”原假设H0，因为总体原假设成立的情况下样本数据出现该结果的概率非常小(但仍存在可能性).我们的总体中明明原假设是正确的，说明此时的推测出错了，而统计上将这种错误拒绝了原假设H0的情况称之为一类错误，而犯一类错误的概率实际上就是所设定拒绝域的对应概率，也被称为显著性水平.例如常见的α=0.05水平，就说明犯一类错误的概率为5%，所以一类错误又名α型错误.需要特别强调的是，即使将显著性水平定义的非常小，也终究有犯错的可能.

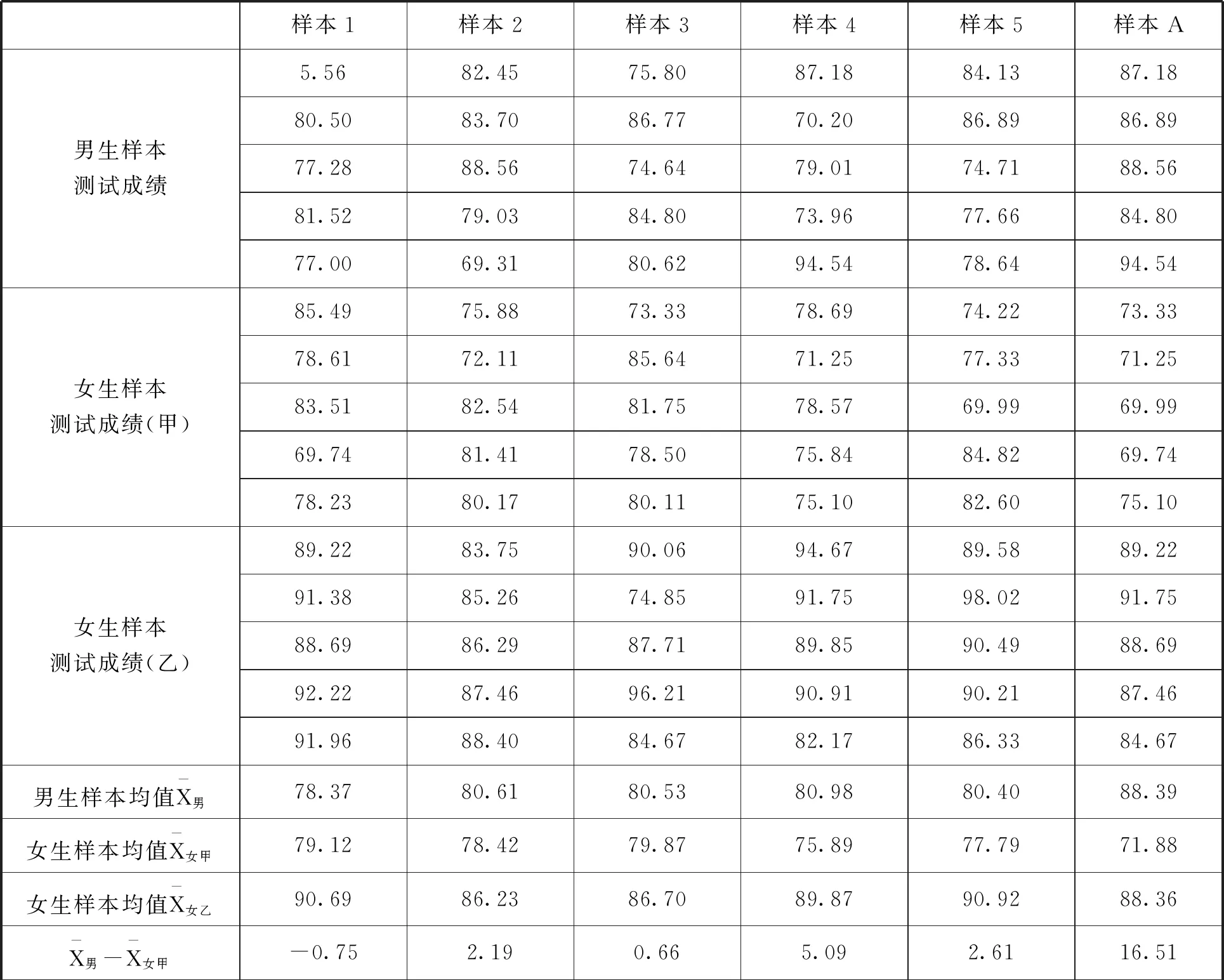
表1 男女生测试成绩模拟数据

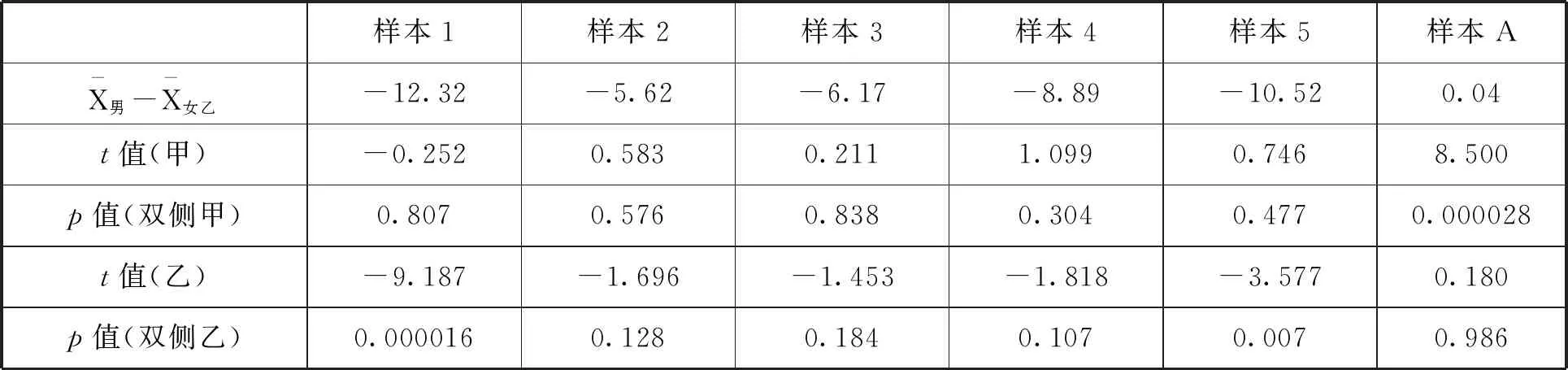
续表

通过这样的示例可以直观地感受到，无论如何总是有犯错的可能性，要么是总体没有差异却推测为有差异(一类错误)，要么是总体有差异却没有检测并推测到这种差异(二类错误).这两种错误在统计学的相关论述中均做了认真详细的阐明[7]，但由于部分研究者错误理解了假设检验的含义，致使在解读统计结果时往往过度依赖假设检验的结果，将统计意义上的“推断”当作真理性的“结论”.

4 关于统计假设的争论及使用中的注意事项

p值的提出者Ronald Fisher教授在20世纪初就强调，其目的是为了有一种客观的方式来描述数据和原假设的相符程度，而不是仅能够粗糙地表示“数据看起来和原假设不一样”.p值是在总体原假设成立的情况下某样本特征出现的条件概率，并不是原假设错误的概率或备择假设正确的概率，最初设定的0.05、0.01等显著性水平也只是一种习惯性的表述.但随着越来越多的研究者盲目追求小p值、错误解读p值含义、将统计显著性和实际效应等价，部分权威机构被迫做出反应，例如美国心理协会(APA)于1999年开始强制要求研究者报告主要结果的效应量.2016年，美国统计协会(ASA)首次以官方身份对统计显著性和p值的争论作出回应，在这份集合了20多个专家意见的报告，认为p值经常被错误地使用和理解，这才导致了一些学术期刊劝阻甚至放弃使用p值[8].Daniel J.Benjamin等人在权威期刊Nature Human Behaviour中发表声明，为了提高研究的可重复性，主张将显著性水平从0.05调整至0.005，他们强调，其实有很多比重新定义显著性水平更好的方式(例如贝叶斯因子)，但调整p值阈限的方式和多数研究者受到的训练习惯相符，是最简单、最容易被快速广泛接受的方式.2018年初，Political analysis的主编Jeff Gill表示，禁止使用p值的主要原因是“p值本身不足以提供支持给定模型或假设的证据”，他同时表示，从一个学术期刊的角度来说，p值常被用来当做稿件是否接受的标准，而这无疑会导致“发表偏倚(publication bias)”并无形中“鼓励了研究者对模型无意义的挖掘”，同时也有证据证明“众多社会科学研究者对p值存在误解，还错把它当成科学推理的关键”，在此背景下，该期刊才决定禁止报告p值.

总结各科研团体、学术期刊和专家学者的观点可以发现，“废除”p值其实是无法制止诸多研究者错误使用假设检验时做出的无奈之举.那么在数学教育研究中，应当怎样正确使用假设检验这一工具帮助我们进行科学的思考呢？以下将从假设检验的使用情境、前期说明、结果解读三方面提出常见的注意事项.结果解读方面，重点关注了三种常见误用——误解p值含义、忽略样本量影响、将统计意义上的显著与实际显著性对等.

第一，需要明确何时进行假设检验：只有当研究者试图做推断时才需要做假设检验，如果只是了解样本情况，例如研究两个班级某次考试的数学成绩，所使用的数据已经是总体，就不再需要做假设检验或统计推断.在数学教育研究领域中，很多以描述为目的的研究，或一线教师对学生表现的分析，并不需要进行假设检验.此时需要注意样本及总体都不一定指的是被试，例如当研究者试图推断两个班级学生的数学能力时，某次数学考试成绩成为了学生数学能力这一总体的样本时，才需要进行假设检验.

第二，需要提前论述样本的代表性：如果确定需要做假设检验，就是在用样本推断总体或模型，因此必须对样本的代表性进行说明.样本的代表性，或样本属于总体的随机抽样，往往是抽样过程中的基本要求.另一方面，利用F检验中的F分布、t检验中的t分布等进行检验，也应当符合该检验对样本随机性的假设.

第三，需要正确理解p值的含义：p值只描述总体满足原假设时样本数据出现该统计量的可能性，属于条件概率，既不是原假设正确的概率，也不是备择假设错误的概率，p值的大小也不能代表效应的强弱.因此，类似“由于p值为0.001，因此我们的结论99.9%是正确的”，“A变量p值为0.06，B变量p值为0.10，A比B更显著”这样的表述都是不科学的.需要特别强调的是，p值未达到显著性水平不代表总体中不存在效应，二类错误仍可能发生.例如在一些量化研究中经过假设检验后，p值未达到显著性水平，并不代表总体的原假设一定成立，如果该研究问题有重要的理论意义，反而应当在后续的研究中进行重复性的考察，避免二类错误发生对有意义研究的终结.

第四，在大样本中发现显著结果应谨慎对待：数学教育研究领域的量化分析经常容易出现大样本的情况，由于包括t值、F值在内的众多用于假设检验的统计量的计算公式都和样本量有关，均值标准差等保持稳定的情况下，样本量越大统计值也会越大；而且样本量增大会导致自由度的增加，统计值的密度函数图像也会发生变化，例如t分布的图像就会变窄，微弱的效应也会非常容易达到统计意义上的显著.因此大样本导致的统计显著需要关注实际效应到底如何.

第五，数学教育研究者应更加关注实际显著性：目前公开禁止报告p值的两个期刊在其声明或对读者问题的回复中都强调，研究中需要的是“科学推理或创造性思维”.事实上假设检验只是总结数据结果的一种手段，作为教育研究工作者更应该重视实际显著性.比如在进行两个班级平均分差异比较的时候，如果两个平均分差异很明显，在解读数据时说到“显著”指的是实际显著性而非统计显著性；再比如在一些大样本中发现男女生平均成绩差异非常微弱但统计意义显著时，这种差异通常并没有实际意义，此时统计意义显著的同时，实际的“不显著”或称之为不客观才更应当是研究者所关注的.

5 结语

依据APA在其2010年发布的出版手册中的表述，“假设检验是起点(starting point)，在这之后增加报告效应量、置信区间和全面的描述才能表达出结果的完整含义”，而“完整地报告所有检验的假设和合适的效应量及置信区间的估计是在APA期刊中发表的基本要求”，因此APA并未否定假设检验和p值的作用.同样的，即使面对越来越多针对假设检验和p值的批评，ASA也从未对取消p值表示赞同.当然ASA也指出p值或假设检验确实不能测量或代表一个效应的大小或一个结果的重要性，这是p值的局限性，但自始至终p值就从未承担过这一作用.效应量等在研究结果中被要求报告的量化结果是对p值局限性的弥补，但效应量反过来也不能提供p值所能提供的信息.

如前文所列举的示例，如果试图了解某种教学干预是否有效果，这时候就需要使用假设检验并报告p值来进行推断，但教学干预效果的重要性，既不能通过p值有多小，也不能通过效应量有多大来进行判定.这种实际显著性需要理论的说明、科学性的思辨和实践的证据来证实，而实际显著性才是包括数学教育研究在内的所有社会科学研究的关注点.