基于稀疏优化的烟羽断层重建方法*
2019-08-29钟鸣宇奚亮司福祺周海金王煜
钟鸣宇 奚亮 司福祺† 周海金 王煜
1)(中国科学院安徽光学精密机械研究所,环境光学与技术重点实验室,合肥 230031)
2)(中国科学技术大学研究生院科学岛分院,合肥 230031)
3)(安徽理工大学电气与信息工程学院,淮南 232001)
1 引 言
燃煤发电在我国能源结构中占比高达65%,为经济社会发展和人民生活提供坚实的能源保障的同时,排放SO2等也给环境带来了巨大的压力.最新的研究表明,大气中的有机物与硫酸在大气新粒子的形成和增长中具有重要作用[1].而燃煤电厂排放的硫超过总量的40%,因此研究电厂SO2的排放情况及空间分布具有重要意义.
差分吸收光谱仪(differential optical absorption spectroscopy,DOAS)仅能测得气体浓度沿光传输路径的积分,而断层图像重建使这种大气参数的间接测量成为实用技术[2],在大气遥感领域得以广泛应用.用于断层重建的光学遥感设备通常仅有2台且固定在地面,气体断层重建是典型的不完全角度重建.早期的研究通过直接解方程来重建气体分布,重建图像质量不高[3-5].一种改进方法是对气体建模作为先验信息,为方程组增加约束.常用的模型有Drescher 等[6]提出的高斯模型、Price等[7]提出的低三阶导数(low third derivative method,LTD)模型和Olaguer等[8-10]提出的基于流体力学的欧拉方程模型.LTD模型假设气体浓度对位置的三阶导数值全部为零,相当于隐含地假设了气体浓度严格满足空间位置的二阶多项式.Johansson等[11]分别将该方法用于重建火山和烟囱烟羽分布.Kazahaya等[12]将LTD项乘以权重系数后和投影方程相加,并使用最小二乘法求解,但重建的结果仍然不够理想.Casaballe等[13]利用LTD模型,对投影方程组进行Tikhonov正则化,并使用cvx优化工具箱进行求解,取得了很好的数值模拟效果,但该方法实际抗误差能力弱,无法用于外场实验数据.总的来说,重建算法还很不成熟,重建图像存在大量伪影.压缩感知(compressed sensing,CS)理论为气体分布重建提供了新的思路: 如果能找到气体分布在某种变换下具有稀疏性,就可以在采样数很少的情况下精确重建气体分布[14-17].
本文使用成像差分吸收光谱仪(imaging differential optical absorption spectroscopy,IDOAS)采集数据,提出了一种基于低三阶模型的全变分(low third derivative total variation,LTD-TV)法重建烟羽分布.该方法基于LTD模型和压缩感知理论对烟羽分布进行重建,首先使用代数重建算法(algebraic reconstruction technique,ART)对重建数据进行初始化,用对数障碍函数法[17]确定目标函数,全变分法确定下降梯度,最后使用Barzilai-Borwein(BB)算法[18]确定步长后对重建结果进行优化.本文对该方法进行了数值模拟,并进行了外场实验,重建了烟囱烟羽的断层2维分布,并对重建结果进行了分析.
2 测量原理与IDOAS断层扫描系统
2.1 测量原理
DOAS技术基于Lambert-Beer定律

其中I0(λ)为大气层外的太阳光强,I(λ)为经过大气层后,DOAS接收到的太阳光强,σm(λ)为第m种气体的吸收截面,

其中Sm表示该种气体的斜柱浓度,等于气体的浓度cm对光程r积分,积分距离为L.通过最小二乘法求解(1)式,可以得到污染气体的斜柱浓度[19,20].
2.2 断层扫描系统
如图1所示,扫描烟羽的过程中,假设风沿Z轴方向,虚拟的扫描平面垂直于大地,烟羽被该虚拟平面截取了一个平面,两台IDOAS放置在扫描平面与大地的交线上.将IDOAS#1指向IDOAS#2的方向设为X轴的正方向,竖直向上设为Y轴正方向.扫描区域离散化如图1中的虚线所示.两台IDOAS的视场角为30°,相邻扫描线间隔0.625°,在2 s内采样并存储48个点的柱浓度数据.而采用以往常用的多轴差分吸收光谱仪(multi-axis differential optical absorption spectroscopy,MAX-DOAS),采集相同数量的数据需要5 min以上.IDOAS采集数据的时间分辨率比MAX-DOAS提高了160多倍.在正式扫描之前先进行预扫描,调整IDOAS的仰角,使烟羽位于IDOAS的视场角内.将扫描区域划分为多个网格,在这些网格上使用重建算法重建烟羽的浓度分布.
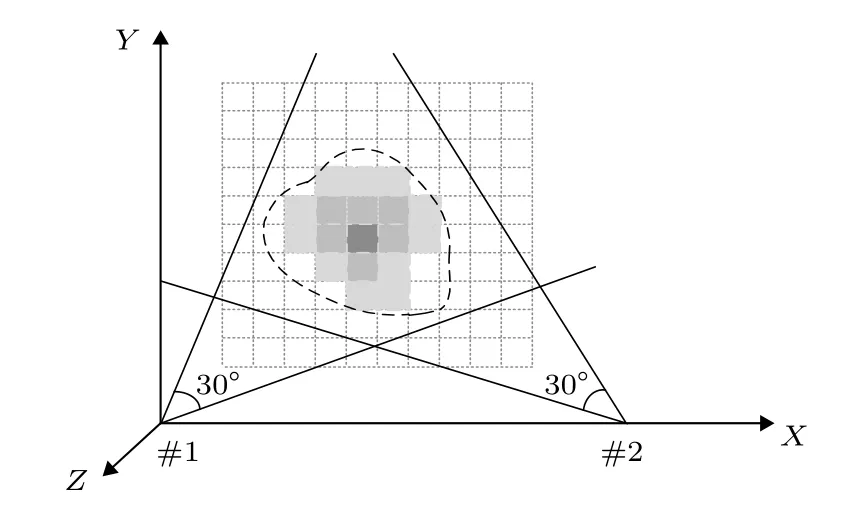
图1 扫描区域离散化Fig.1.Scanning region discretization.
3 重建算法
在离散情况下,(2)式可表示为

S(i)为 第i条射线的路径积分浓度,C(j)表示扫描区域第j个像素中的气体平均浓度,H(i,j)表示第i条射线穿越第j个像素的长度.把整个系统的投影系数和浓度写成矩阵与向量相乘的形式

其中H表示投影矩阵,C表示图1中重建区域中像素中排列成的列向量,通常C中像素的数目远大于S中射线的数目,所以(4)式是一个欠定方程组.
3.1 传统LTD算法
为了解方程组(4),LTD模型假设气体浓度相对位置的三阶导数等于0[7],于是有


式中c(k,l)是图1所示重建区域中像素矩阵c的第k行l列像素.把(5)式和(6)式改写为矩阵的形式

将(4)式和(7)式联立得到一个过定方程组,求解就得到了浓度C的近似值.
3.2 LTD-TV算法
在传统的LTD方法中,隐含地假设气体的浓度是位置的二阶多项式.然而,气体的浓度不可能严格地按二阶多项式分布,(7)式左端直接设为零显然会导致图像像素间约束过强,图像边缘出现大量伪峰,严重影响重建气体的实际分布.而本文提出的LTD-TV算法,仅要求气体的浓度大体按照二阶多项式分布,也就是假设气体浓度值在三阶导数下是稀疏的,该假设显然比(7)式合理得多.
LTD-TV法首先使用ART算法对重建图像进行初始化,然后使用基于全变分的优化算法优化目标函数.目标函数为

式中C∗即为所求的气体浓度分布,表示气体浓度分布的全变分的模,ε和镜头接收的光子数目的泊松分布有关,这里简单设置为10—12,不作进一步的深入讨论.使用对数障碍函数法[17],方程(8)中的约束条件可以写入优化问题中

如果使用低三阶导数模型,根据(5)式和(6)式,(9)式中气体分布的全变分表达式为

对(9)式右边括号中的部分求导,得到(9)式的梯度为

(11)式中,全变分的梯度的计算公式为
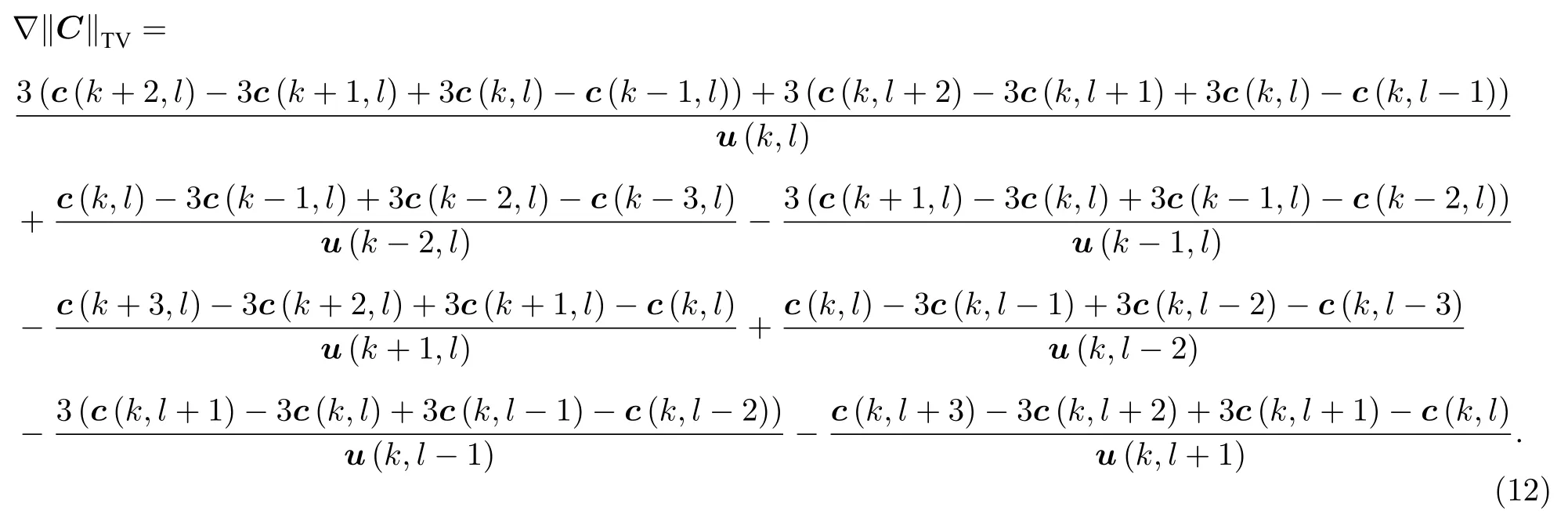
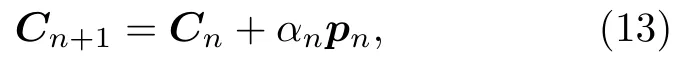
使用优化算法求解(13)式,αn是优化算法的步长,pn是优化算法的下降方向.

式中的gn(j)由(11)式确定,j和(3)式中j的含义相同,表示第j个像素,(14)式隐含地给气体浓度添加了非负约束.(13)式中αn用BB算法得到

式中sn-1=Cn-Cn-1,yn-1=pn-pn-1,分别表示前后两次迭代的气体浓度分布差,和前后两次迭代的梯度差.当(13)式中两次迭代间的图像差别很小时,说明算法收敛.
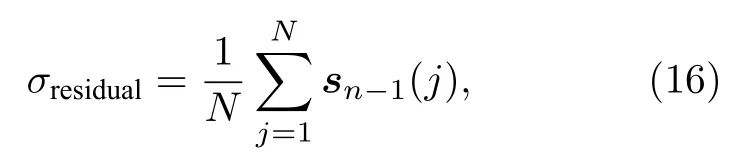
式中N表示图像中像素的总数.当σresidual小于某个阈值,或者迭代次数大于某个数时迭代停止.
4 数值模拟
假设真实的气体浓度分布服从高斯模型,扫描系统如图1所示,两台IDOAS分别位于X轴的左右两端,Y轴代表气体所在的高度,扫描线间隔为0.625°,重建图像解析度为 20×20.为了比较方便,将高斯函数的浓度归一化为1.在知道气体真实分布的情况下,使用接近度σnearness作为重建效果的指标
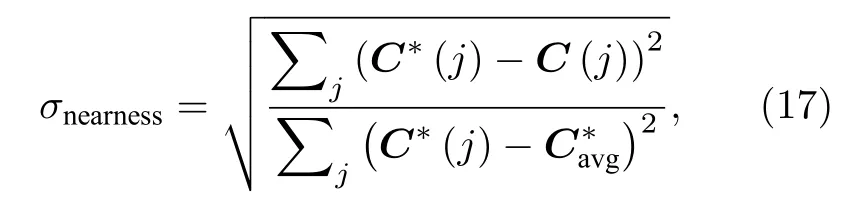
其中C∗(j)是测试图像第j个像素中的气体浓度,C(j)是 重建图像第j个像素的气体浓度,是所有像素气体浓度的平均值.接近度越小,重建效果越好.
4.1 LTD-TV算法与传统LTD算法重建结果对比
图2给出几幅用传统的LTD算法和LTD-TV算法重建气体分布的数值模拟等高线图.图2(a)—图2(c)分别是单高斯、双高斯、三高斯气体扩散模型.
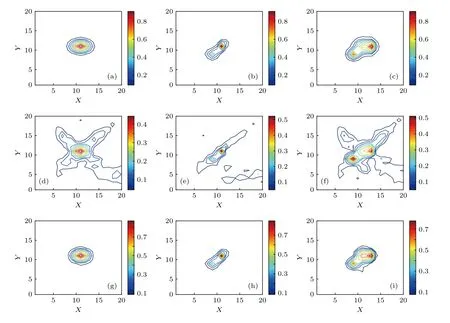
图2 传统LTD法与LTD-TV法比较(a),(b),(c)测试图形;(d),(e),(f)传统LTD法重建图形;(g),(h),(i)LTD-TV法20000次迭代重建图形Fig.2.Comparison between traditional LTD algorithm and LTD-TV algorithm:(a),(b),(c)Test distribution;(d),(e),(f)reconstruction of distribution using traditional LTD algorithm;(g),(h),(i)reconstruction of distribution using LTD-TV algorithm with 20000 iterations.
图2(d)—图2(f)使用传统LTD法重建,接近度分别为0.6363,0.5930,0.5778; 图2(g)—图2(i)是在循环20000次的情况下用LTD-TV法重建,接近度分别为0.1127,0.1052,0.1995,分别比传统的LTD算法接近度减小82.28%,82.25%,65.47%.从图2中可以看出,LTD-TV法重建图形相比传统的LTD法有很大的改善,大大减小了重建的伪影.该算法不但能重建出烟羽扩散的大致情况,还能重建出丰富的细节.然而,LTD法假设气体浓度是位置的二阶多项式,重建过程其实是用二阶多项式去拟合高斯函数,导致其峰值浓度比真实浓度低10%—15%,扩散范围比测试图形稍大,总体上有变圆的趋势.
4.2 测量误差对重建结果的影响
外场实验中,温度、湿度、气溶胶等都会影响DOAS的精确性.SO2的测量值往往具有2%—20%的测量误差,不好的重建算法可能会使误差在整个图形扩散,造成重建结果偏离真实值,甚至完全淹没在重建噪声中.因此,重建算法的抗误差能力是考察重建算法的一个重要方面.由于误差来源的复杂性和不可重复性[22,23],一般采用叠加随机数的方法模拟误差对测量的影响[13].给图2中测试图形的路径积分浓度Sk加入加性噪声ΔSk

式中f表示误差系数,Rrand是方差为1的随机数.图3给出了f从1%—20%变化的情况下,用LTD-TV重建图2中的测试图像得到的σnearness曲线.
从图3可以看出,随着误差系数f变大,LTDTV算法的重建接近度也逐渐变大.当误差系数达到某个值时,接近度的上升变慢,说明误差越大,LTD-TV算法的抗误差效果越明显.从图3还可看出高斯数为2时重建误差最小,对比图2(a)—图2(c)可以看出,高斯数为2的测试图形的非零元素最少,图像本身的稀疏性最强,因此LTDTV算法的性能也发挥得更加充分.而在误差系数f变化的情况下,传统LTD算法重建接近度仍然为0.6363,0.5930,0.5778,比使用LTD-TV法重建的接近度更大.总的来说,LTD-TV算法比传统的LTD算法的重建质量好得多.

图3 接近度随误差系数变化曲线Fig.3.Nearness as the functions of error factors.
4.3 大气流动对重建结果的影响
已有的研究表明,当烟羽位于重建图像的中心,且两台DOAS与烟羽中心的连线之间成90°夹角时,重建效果最好[11,13].由于风向的不确定性,该条件往往得不到满足.图4中给出了图2(a)—图2(c)中高斯烟羽模型偏离初始位置时,接近度随偏离距离变化的曲线,偏移距离小于0时,表示烟羽位置左移,偏移距离大于0时,表示烟羽位置右移.
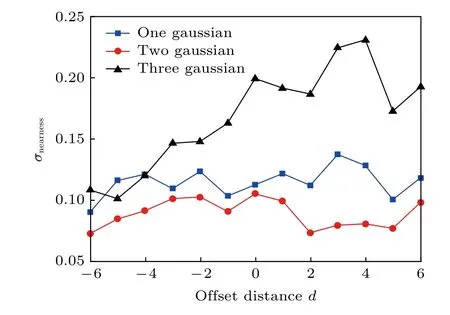
图4 接近度偏离距离变化曲线Fig.4.Nearness as the functions of offset distance.
从图4中可以看出,当烟羽偏离图像中心时,重建接近度和气体分布的稀疏性仍然相关.当单高斯烟羽和双高斯烟羽偏离初始位置时,重建图像的接近度发生振荡,这种振荡是重建图像离散化造成的,与以往的算法相类似[11].除此之外,接近度曲线未表现出明显的变化规律,说明烟羽稀疏度较高的情况下,LTD-TV算法不受烟羽与IDOAS相对位置的影响.而当三高斯烟羽模型偏离图像中心时,重建接近度发生变化.这是因为烟羽重建是一种极端的不完全角度重建,当烟羽中气体浓度分布较为复杂时,不同的烟羽位置会对IDOAS采集数据造成较大的影响,从而造成重建效果发生起伏.此外,外场实验时,特别是在湍流的影响下,要表示烟羽中气体浓度的复杂分布,需要更多的像素数目.从信息论的角度来看,在两台IDOAS信息采集能力有限的情况下,低三阶导数模型增加的先验知识会将IDOAS采集的数据淹没,导致重建结果偏离真实分布.因此,如果需要进一步提高LTDTV算法的重建图像的分辨率,只能进一步增加仪器的数量[5,24].
基于烟羽位置与形状的复杂性,使用LTDTV法时仍然建议将IDOAS关于烟囱对称设置,且两台DOAS与烟羽中心的连线之间成90°夹角.
5 外场实验
外场实验数据在淮南某电厂外获得,电厂烟囱高210 m,在下风约180 m处搭建由两台IDOAS组成的断层扫描系统,两台仪器距离约504 m.实验当天天气晴朗且能见度高,风向为东北偏东风,风速为 2 m/s.通过 307.5—318 nm波段反演SO2路径积分浓度,参与反演的气体包括SO2(293 K,vanDaele),NO2(294 K,vanDaele),O3(243 K,Voigt),O3(218 K,Brion)和ring光谱,选取烟囱上风向的第一次测量谱作为参考谱.图5以其中某一条光谱为反演实例,展示了SO2光谱数据的反演情况.

图5 SO2柱浓度IDOAS拟合反演实例(a)SO2柱浓度;(b)拟合残差Fig.5.An example of SO2 SCD from IDOAS retrieval:(a)SO2 SCD;(b)fitting residual.
图5(a)中黑线(不规则曲线)为测量光谱,红线(光滑曲线)为拟合光谱,SO2柱浓度为1.11×1017molecules·cm—2.图5(b)所示的拟合残差小于0.00322.选取其中一组SO2数据作为研究对象,由于气体浓度不可能为负,重建图像时,小于零的路径积分浓度被设置为0[5].图6给出了使用LTDTV法重建的污染气体断层图像.
在图6中,IDOAS#1位于X轴0点,IDOAS#2位于X轴504 m处.烟囱中排出的SO2在空中分成两股,符合现场目测.能够非常清楚地看到烟羽从两个中心扩散的情况,甚至可以观察到风向在略微向IDOAS#2的方向变化,SO2截面向该方向移动.重建图中仅有右下角存在少量伪影,其他位置有零星伪影,不影响对重建图像的观察.IDOAS测得的柱浓度与重建图像的柱浓度值之间的关系如图7所示,直观上看,柱浓度的测量值与重建值符合得很好.
当气体分布未知时,一般使用一致性相关因子衡量重建效果[21].


图6 烟囱烟羽SO2分布重建图Fig.6.Reconstruction of SO2 of stack plume.
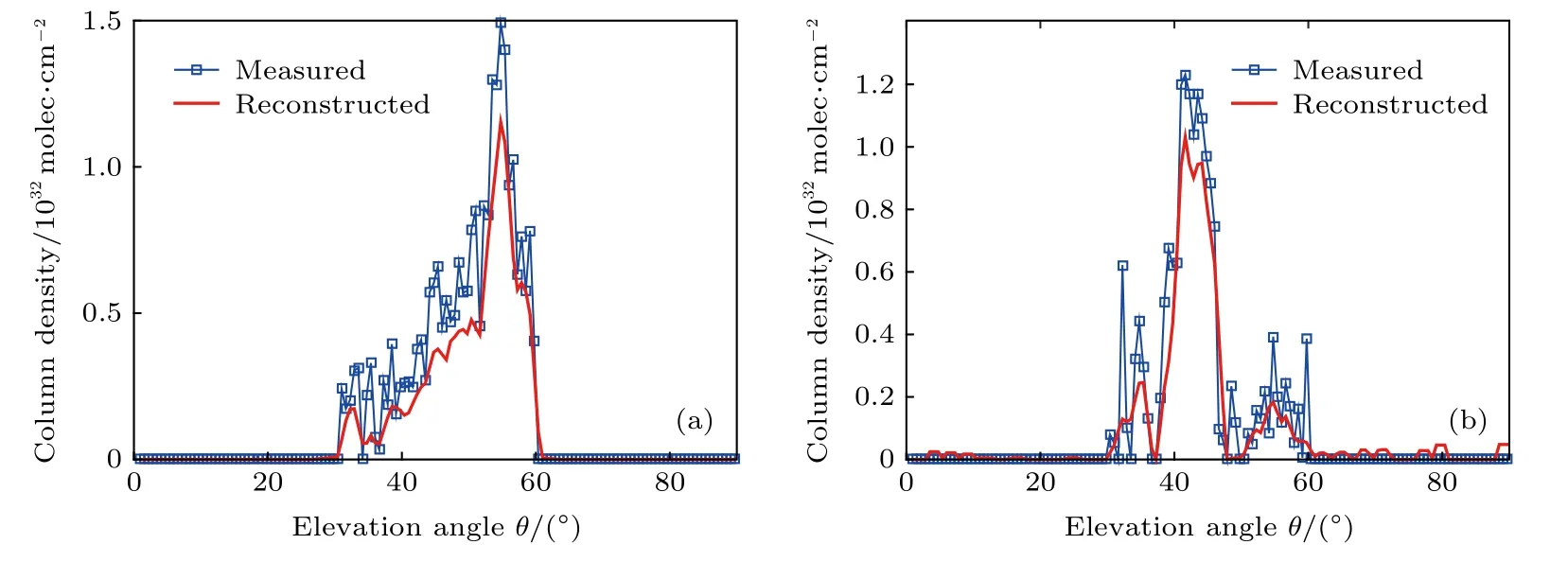
图7 测量路径积分浓度与重建路径积分浓度对比(a)IDOAS #1;(b)IDOAS #2Fig.7.Comparison between measured path integrated concentration and reconstructed path integrated concentration:(a)IDOAS#1;(b)IDOAS #2.
式中ρ表示皮尔逊相关系数,A是路径积分浓度曲线发生位移时的校正因子,
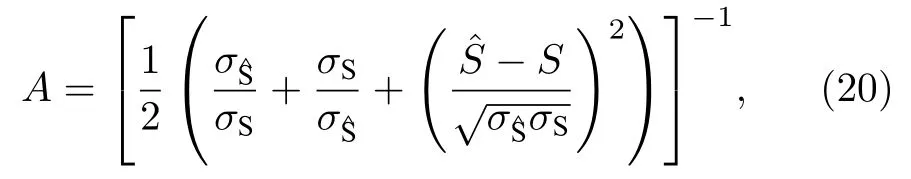
其中S是IDOAS测得的路径积分浓度,σS是测得的路径积分浓度的标准差;是重建图像的路径积分浓度,是重建图像路径积分浓度的标准差,如果CCCF>0.80 ,即可认为重建图像的路径积分浓度和实验测量值拟合得很好,而图7所示重建结果的一致性相关因子为0.9063.重建得到的路径积分浓度比测量值稍低,符合数值模拟中出现的情况.
6 结果与讨论
本文首次将CS理论引入气体断层重建领域,提出了一种新的气体分布重建方法—LTD-TV算法.数值模拟表明,该方法将接近度由传统LTD法的0.5—0.6降低到0.1—0.2,最大降低幅度达82.28%.针对加性噪声,LTD-TV法表现出很强的抗噪声能力,在路径积分浓度中引入20%的加性噪声的情况下,LTD-TV法仍然能重建出气体扩散的主要特征.在外场实验中使用IDOAS采集数据,并重建了的烟羽分布图形.该方法不但假设气体的三阶导数是稀疏的,而且隐含的假设气体浓度值非负,相当于给投影方程组添加了更多的约束.因此与以往的烟羽重建方法相比,提高了气体重建的时间分辨率和可信度,极大减少了伪影.该方法不但能用于竖直方向的烟羽分布重建,还能用于水平方向的区域气体分布重建.不足之处在于: 使用二阶多项式作为气体扩散模型,当气体近似按高斯函数分布时,重建结果的峰值偏低,扩散范围偏大.
