基于二阶段差分演化的WSN节点定位优化

(广东工程职业技术学院 信息工程学院, 广州 510520)

0 引言

无线传感器网络(wireless sensor networks, WSN)作为物联网应用技术的核心组成部分，通过节点的自组织，具有无中心性、动态性，成本低、功耗低、节点设置灵活、大规模、自适应能力强、可扩展性好的特点[1]，使信息的传播、处理及应用形成了新的模式，实现了物联网技术与真实物理世界的结合。随着物联网技术的快速发展和应用领域的不断扩大，已广泛应用于国防部署战场监测、地质监测及勘查、车辆跟踪交通整治、应急救援人员营救等具有特殊需要的通信环境中[2]。WSN自组织地通过传感器收集数据，通过无线电波随机地相互通信。由于传感器节点分布的环境很复杂，常分布在数据不方便收集与传输的复杂环境，或者目标位置会不断移动的区域，例如水下，火灾，火山，动物栖息地或战场等，而使用全球定位系统(GPS)成本高昂且在室内不可行，所以需要通过无线电协作方式收集、传播以及处理目标区域的数据信息，因此WSN中的节点位置信息成为重要内容。如何使节点的位置计算更接近实际已成为目前无线传感器网络定位研究的热点，无线传感器网络应用关键技术之一的WSN自定位技术近年成为学界研究的关注热点[3]。

定位算法分为基于测距和基于免测距两种，基于测距的定位算法由于使用了测量设备，所以定位精度很高而得到广泛应用[4-7]，但此方法也受到周边复杂环境的影响，定位精度会出现较大误差，RSSI算法是这类算法的典型，定位正确率非常高，但缺点是要增加额外设备，并且实际使用中会发生测量信号损耗，总体来说这类算法代价高。基于免测距的定位算法不需要测量，不需要额外增加设备，实现较简单，但往往定位误差更大[8-10]，典型的是DV-Hop算法，实现较简单，应用很广泛，但误差较大，精度有待提高。

在DV-Hop算法依赖整个网络的连通度，根据节点间的平均跳距和跳数来定位，虽然近年有学者采用各种方法对结果进行修正，但最后修改结果误差还是偏大，在30%左右。近年有不少学者针对DV-Hop算法存在的不足，为提高节点的定位精度，采用遗传算法、模拟退火算法、粒子群优化算法等对DV-Hop进行优化，特别是遗传算法和粒子群优化算法成了研究热点，取得不少研究成果[11-16]，但这些优化算法存在迭代次数相对过大，节点耗能相对较高的缺点，为解决这问题，本研究提出一种基于二阶段优化的的差分演化算法，在DV-Hop定位的基础上，采用差分演化算法进行第二阶段定位优化的方法，通过仿真验证，证明了该算法在很低的迭代次数(能耗很低)就能获得较高的定位精度，为WSN定位研究探索一个新思路。

1 DV-Hop无线传感器节点定位算法

DV-Hop算法作为一种典型的免测距算法，应用广泛，其工作过程为：

1)类似距离矢量交换协议，首先，信标节点用无线电信号向相邻节点广播包括自己位置及跳数的数据，并设初始跳数为零。通信范围内的节点接收到数据后保存这个信标节点坐标并把这个信标节点发送过来的跳数值增加1，按照最小跳数原则更新自己的路由表，之后再向自己相邻的其他节点发送信息，如此重复上述步骤，经过一轮洪泛广播，除了一些无法获得广播数据包的边缘节点和孤立节点外，整个WSN节点都将获得距离信标节点的最小跳数值。这样，每个节点都记录了到所有信标节点的最小跳数。

2)计算平均跳距。平均跳距是根据信标节点之间的跳数-距离关系推导出来的。根据上一步骤，每个信标节点获取了能够与之通信的其他信标节点的位置坐标和最小跳数，假如信标节点i和信标节点j的实际坐标分别是(xi,yi)和(xj,yj)，上一步骤已经得到了这两者之间的最小跳数hopsij，则可以根据式(1)计算平均每跳的距离值[9]。

(1)

每个信标节点将自身对应的Ci广播到整个WSN中，未知节点只保留距离自己近的信标节点的平均每跳距离值Ci，其他全部舍弃，并将其发送到附近的节点。如果未知节点m到信标节点i的最小跳数hopmi，则未知节点m到信标节点i的估计距离如式(2)所示：

dmi=Ci×hopmi

(2)

3)计算未知节点坐标。经过以上两个阶段，未知节点利用式(2)可以获得到多个信标节点的估计距离(需要三个或以上)，用三边测量法确定未知节点的定位。设第i个信标节点坐标为(xi,yi)，待定位的未知节点坐标为(x,y)，待定位的未知节点与信标节点i之间的距离为di，根据上述已知数据，可建立方程组如式(3)所示:

(3)

对方程组(3)采用极大似然估计法进行求解，得到方程组(4)：

(4)

将方程组(4)用矩阵形式表示：AX=B。

其中：

(5)

(6)

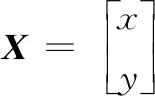
(7)

使用最小二乘法，可得到未知节点坐标如式(8)所示:

X=(ATA)-1ATB

(8)

设待定位的未知节点(x,y)与信标节点(xi,yi)的实际距离是ri，测距误差为εi，可知ri-di<εi。

则待定位的未知节点坐标(x,y)应满足式(9)的约束条件：

(9)

求解(x,y)，得：

(10)

综上所述，未知节点定位问题可以转化为一个多约束优化问题，式(10)是一个非线性优化问题，数学上难以精确求解，因此研究利用差分演化算法进行二阶段精确求解。

2 基于差分演化的二阶段定位优化算法

2.1 差分演化算法

差分演化(Differential Evolution,DE)是由 Storn 和 Price 科学家在 1995 年提出的一种启发式随机搜索算法，跟遗传算法、粒子群算法一样属于群体智能仿生算法，具有结构简单、容易实现、收敛速度快、鲁棒性强等优点[11]，该算法具有极强全局搜索能力的演化算法，因其在第一届IEEE 演化大赛中的超群表现引起了国内外学者的极大关注，近年成为研究热点，已被广泛应用到各种优化领域中，该算法适合用到WSN定位优化领域。

差分演化是一种在遗传算法等进化思想的基础上，基于群体差异的启发式随机搜索算法，与其他进化算法大体上流程大致相同，也包含了种群初始化、变异、交叉、选择等操作。不同之处在于，差分演化算法是的核心是变异操作，将多个向量的差分信息作为基向量的扰动量，先从群体里随机选两个个体向量进行差分和缩放，再与该群体中随机选定的第三个个体向量相加，得到一个新的变异个体向量，然后这个新的变异个体向量与父个体向量进行杂交，形成了一个备选个体向量，最后比较备选个体和父个体的适应值，采用贪心策略，总是选择较优者保存到下一代群体中。这样，差分演化算法利用差分变异、杂交和选择等算子对群体不断进行演化，直到达到终止条件为止。

经过多年的发展，DE有多种不同的进化模式，差别体现在算子的变异方法不同，这里采用DE/rand/1模式。而作为个体优劣评价的函数将采用式(11)：

(11)

2.1.1 变异操作

采用DE/rand/1模式，设向量D为维数，本文为无线传感器网络中的未知节点坐标值。从种群中随机选择3个Vi(t+1)=(Vi1,Vi2,…,ViD)染色体Xr1,Xr2,Xr3，且i≠r1≠r2≠r3，则：

Vij=Xr1j+F×(Xr2j-Xr3j)

(12)

其中:Vi为变异向量；Xr2-Xr3为分差向量；F∈[0,1]为缩放因子；t为当前演化代数。

2.1.2 杂交操作

杂交算子对变异向量Vi和父个体向量Xi进行杂交，操作如式(13)所示：

(13)

其中，randrealj是(0,1)之间的随机小数，jrand是[1,D]之间的一个随机整数；CR∈(0,1)是交叉概率。这种杂交策略保证向量Ui至少有一维来自变异向量Vij，避免与父代个体向量Xi相同而过早停止了进化。

2.1.2 选择操作

采用贪婪策略，总是选择较优者保存入下一代群体里，如式(14)所示:

(14)

其中，f为适应函数，i=1,2,…,NP，NP为种群规模。

2.2 二阶段定位算法

近年学界利用各种智能算法比如遗传算法、粒子群优化算法对无线传感器网络定位进行优化[1-11]，采得不少成果，定位误差由30%提高到5%左右，效果良好，但是也存在优化迭代代数过高的明显缺点，这些优化算法普通都在迭代1000代以上，最少也要500代以上，将耗费较大的能量，在能量存储不大的各无线传感器节点的实际应用中，追求高精度的同时，也要追求低能耗，所以寻找更少迭代次数(即更低能耗)算法成了当务之急。

为了提高定位精高的同时更低能耗(更少迭代次数)，本文研究了二阶段定位算法，第一阶段用DV-Hop无线传感器节点定位方法找出未知节点坐标(xest,yest)，第二阶段用差分演化算法在坐标(xest,yest)附近寻找最优坐标(x,y)，即为最终定位的坐标。

具体步骤如下：

Step1:DV-Hop无线传感器节点定位，利用式(1)～(8)计算出未知节点的坐标(xest,yest)。此为第一阶段；

Step2:第二阶段：利用差分演化处算法寻找未知节点的最终坐标(x,y)：

Step2.1 初始化种群。二阶段定位法区分其他定位法在于，种群一开始的位置不是完全随机，而是基于第一阶段定位结果来作种群的初始随机位置，即在坐标(xest,yest)附近以通信半径r范围内的区域作为种群的初始随机位置。

Step2.2 采用式(11)作为个体适应度函数值进行计算，经过式(12)～(14)进行变异、杂交、选择操作。

Step2.3 达到最大迭代数G，停止演化，否则返回Step2.2继续演化。

Step2.4 根据最优个体的位置确定未知节点的最终坐标。

Step2.5 每个未知节点都经过上述Step2.1-4的计算，最终得出所有未知节点的坐标。

3 仿真结果与分析

3.1 实验设计

为了验证本研究的节点定位算法性能优劣，在Widnows 7操作系统下，用Matlab 2016b进行仿真。在100 m×100 m正方形的区域内，随机分布无线传感器节点100个，如图1所示，邻居连接如图2所示，DV-Hop定位误差如图3所示。

考虑到了为了体现更低能耗(更低迭代数)，本研究将只迭代10代。为了使本研究的算法有可比性，除了本研究的二阶段DM算法外，还采用了基本DV-Hop算法、传统差分演化算法Origin_DM、传统粒子群优化算法PSO进行对比，取5次实验平均值作为最终结果。

3.2 结果与分析

3.2.1 定位误差与信标节点数量关系

实验结果如图4所示，分析：

1)相对于DV-Hop算法，三种智能优化算法都对定位精度有明显的提高，特别是信标节点数量20个以上(信标比例大于等于20%)时，DV-Hop算法定位误差率都在30%以上，而三种智能优化算法定位误差率都在10%以下，智能优化算法对定位精度提高具有非常明显的效果。

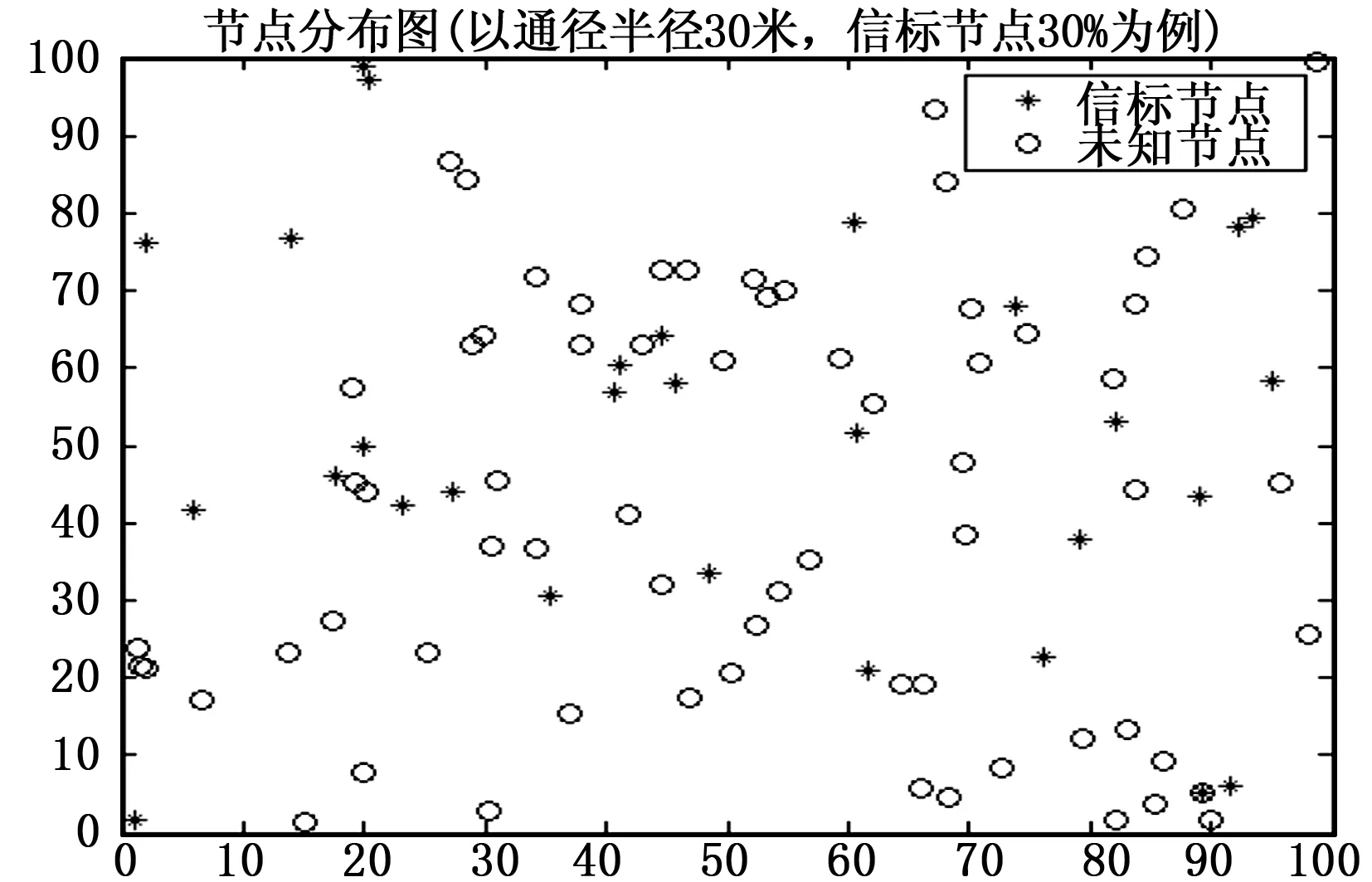
图1 节点分布图(以通径半径30米，100个节点，信标节点30%为例)

图2 邻居关系图(以通径半径30米，100个节点，信标节点30%为例)

图3 定位误差图(以通径半径30米，100节点，信标节点30%，DV-Hop算法为例)

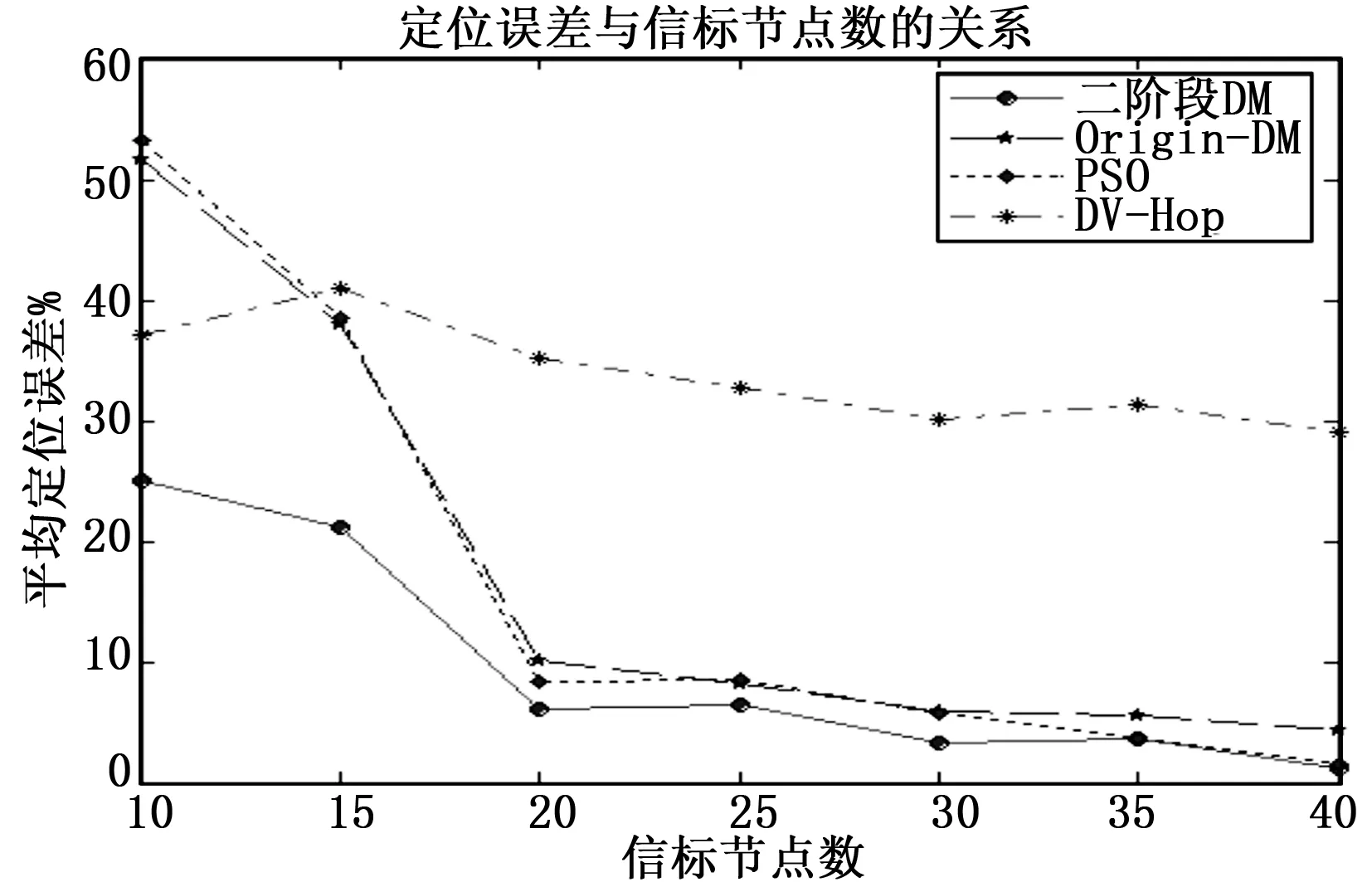
图4 定位误差与信标节点关系

2)在较少信标节点(信标数量小于20，即信标比例低于20%)时，作对比的两种智能优化算法定位精度不理解，在极端情况下(信标节点小于15，即信标比例低于15%)时甚至出现定位误差比DV-Hop更差的情况，原因在于传统智能搜索的优化算法在极度缺少信标节点的信息时，出现无法进一步搜索优化的现象。

3)本研究提出的二阶段DM算法比其他算法有更高的定位精度，并且能很好地解决了上面第2点发现的其他智能优化算法的缺陷，在信标节点极少的条件下，还能得到很好的定位精度。原因在于本研究的二阶段差分演化定位算法是基于第一阶段得到的DV-Hop定位结果，有效地避免了信标节点稀疏时无法有效优化的缺陷。

4)从不同信标节点数量的仿真结果可以发现，本研究算法不但在较多信标节点时有更高的定位精度，而在信标节点稀疏时有更好的表现。

5)总的来说，本研究算法对提高未知节点定位的精度效果明显，说明了本研究算法的有效性。

3.2.2 定位误差与通信半径关系

实验结果如图5所示，分析：

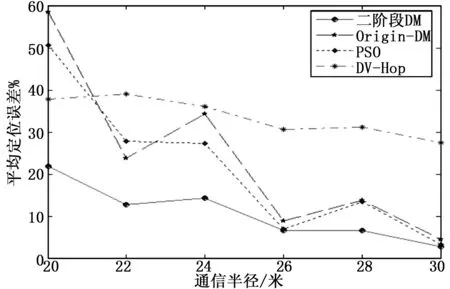
图5 定位误差与通信半径关系

1)跟上面的分析类似地，作对比的两种传统智能优化算法在通信半径22米以上的，都比DV-Hop更好的定位精度，但在通信半径小于22米时，出现了反而不如DV-Hop的现象，原因在于通径半径更短时，邻接节点会明显减少，传统智能优化算法将无法搜索到足够有效信息导致无法进行有效优化的现象。

2)两种传统智能优化算法定位精度出现了波动较大的现象，并且波动规律类似，原因在于传统智能优化算法是随机搜索，容易陷入局部最优，明显影响了定位精度。

3)本研究算法有效解决了上面1、2点分析的传统智能优化算法缺陷，不管在通信半径短的特殊条件下，还是在定位精度的稳定性方面，都比其他智能优化算法表现得更好。总的来说，本研究算法具有更好的定位精度，更好的稳定性。

4 结语

针对WSN定位问题，在分析DV-Hop算法的不足和其他应用在WSN定位的智能优化算法迭代次数较大耗能较多的缺陷，提出一种基于二阶段的差化演化的WSN定位优化算法，经过仿真实验验证，在只需要迭代10代的情况下，证明了本研究算法不但有效提高了定位精度，并且在信标稀疏和通信半径较短时具有更好的稳定性。