基于改进渐消记忆滤波的动力定位状态估计*
2019-08-29徐海祥余文瞾李文娟陈亚豪
蒋 帆 徐海祥 余文瞾 冯 辉 李文娟 陈亚豪
(武汉理工大学交通学院1) 武汉 430063) (武汉理工大学高性能船舶技术教育部重点实验室2) 武汉 430063)(江苏科技大学海洋装备研究院3) 镇江 212003)
0 引 言
动力定位船舶需要从混有高频信号及环境噪声的传感器位置信息中估计出低频运动信息.准确的状态估计直接影响到动力定位船舶的控制性能.贝叶斯最优滤波理论是非线性系统状态估计的基础,而基于贝叶斯理论的卡尔曼滤波也被广泛地应用于动力定位船舶的状态估计中.然而,卡尔曼滤波需要系统具有精确的数学模型,且复杂的海洋环境使得噪声统计数据不充分,这些限制条件会导致新测量值对预测值的修正作用下降,而旧测量值的作用相对提高,最终导致常规卡尔曼滤波的精度有所下降,甚至出现发散.
渐消记忆滤波在卡尔曼滤波的基础上,通过引入渐消记忆因子,减小陈旧测量数据对状态估计值的影响,增大新进测量数据的影响,从而提高滤波精度.Hajiyev等[1]提出一种多重渐消因子的自适应滤波器,通过计算得到矢量形式的渐消记忆因子,对误差估计量采用较小的权重,进而修正估计误差,提高滤波精度,并通过仿真实验验证其算法的有效性,但是这种方法的渐消因子计算复杂,且不适用于动力定位这种每个状态估计量等权重的状态估计.Lim等[2]利用遗传算法优化渐消记忆因子,实现对电池开路电压的在线估计,并通过实验验证该方法的有效性.Chen等[3]将渐消记忆的思想引入H∞滤波中,验证了在模型存在较大误差的情况下该算法的鲁棒性.鲍水达等[4]针对平方根容积卡尔曼滤波在系统模型不准确和状态突变情况下鲁棒性差的问题,引入强跟踪思想,提出了一种多渐消因子平方根容积卡尔曼滤波算法,通过多渐消因子实时调整增益矩阵,以提高滤波稳定性.Wang等[5]为提高LED芯片的定位精度,设计双速率自适应渐消卡尔曼滤波器,引入自适应的渐消记忆因子,提高系统状态估计的鲁棒性.尽管渐消记忆滤波在惯性导航、芯片精确定位等方面的研究与应用已较为广泛,但是在动力定位方面的相关研究与应用却鲜见.张闪等[6]首先将渐消记忆滤波引入动力定位的状态估计中,通过滤波发散评价标准推导出渐消记忆因子的计算表达式,并通过仿真实验验证其有效性,但是由于该方法并不能保证新息序列协方差的不相关性,所以通过该方法得到渐消记忆因子也并不是理论上的最优解.
针对上述问题,本文采用一种新息序列协方差估计器对当前时刻的新息协方差进行估计用以求取渐消记忆因子,避免进入苛刻的条件判据,且这种推导过程是充分必要的,进而修正一步预测状态估计误差协方差,最终提高滤波精度.为验证本文设计算法的有效性,对其进行滤波仿真并与文献[6]的算法进行仿真结果对比.
1 数学模型
船舶非线性运动模型[7]为
(1)
式中:Ah为包含谱峰频率ω0和相对阻尼系数ζ的常值矩阵;ξh为船舶高频状态向量;Eh为表示高频噪声的幅值矩阵;wh为零均值高斯白噪声;ηh为船舶高频运动向量;Ch为系数矩阵;η为低频运动位移矩阵;R(ψ)为坐标转换矩阵;ν为速度矩阵;b为未知环境力矩阵;Tb为包含时间常数的矩阵;Eb为表示未知环境力噪声的幅值矩阵;wb为零均值高斯白噪声;M表示船舶惯性矩阵;D表示船舶阻尼系数矩阵;τ为推进器产生的控制力和力矩;Ev为表示过程噪声的幅值矩阵;wv为零均值高斯白噪声;y为船舶测量位置;vy为零均值高斯白噪声.
将非线性运动模型线性化,得到线性状态空间模型为
(2)
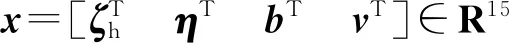
2 常规渐消记忆滤波
将式(2)进行离散化处理之后可得离散状态模型和测量模型:
x(k)=Φx(k-1)+Δu(k-1)+Γw(k-1)
y(k)=Hx(k)+vy(k)
(3)
式中:Φ=exp(Ah),其中h为采样周期;Δ=A-1×(Φ-I)Β;Γ=A-1(Φ-I)E;w(k)和vy(k)分别为系统过程噪声和测量噪声.
系统过程噪声和测量噪声的统计特性满足:
(4)
式中:Q(k)为过程噪声协方差;R(k)为测量噪声协方差;δkj满足:
(5)
根据文献[6],渐消记忆滤波器方程可写为
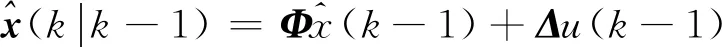
(6)
ΓQ(k)ΓT
(7)
K(k)=P(k|k-1)HT·
[HP(k|k-1)+R(k)]-1
(8)
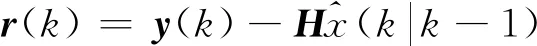
(9)

(10)
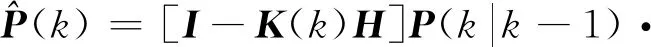
[I-K(k)H]T+K(k)R(k)K(k)T
(11)
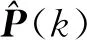
选取不等式作为判断滤波器发散的边界条件:
rT(k)r(k)≤γ(k)trace(S0(k))
(12)
式中:γ(k)为冗余度储备系数,γ(k)≥1;S0(k)为新息序列协方差,S0(k)=E[r(k)rT(k)].
取最严格的判断滤波器是否发散的评价标准,即γ(k)=1,那么λ(k)的求解公式为
ΓTΗT-R(k))(ΗΦP(k|k-1)ΦTΗT)-1]
(13)
式中:m为测量值的维数.
3 改进渐消记忆滤波
文献[6]通过最严格的判断滤波器是否发散的评价标准,即γ(k)=1,以推导出渐消记忆因子的计算表达式.但是,在实际工程应用中γ(k)的取值会受到环境随机性以及人为因素的影响,很难得到合理有效的经验值[7].为此,文献[8]采用一种指数渐消因子滤波算法,当动力定位系统模型不精确、噪声统计数据不充分时,通过实测新息平方和与理论新息协方差的迹的比值来确定储备系数γ(k),进而确定渐消因子,该算法具有一定工程实际应用价值,然而,通过收敛判据得到的渐消记忆因子并不是最优的,也就是说该算法对新息序列的利用程度不是最高的,所以此时滤波器的性能也不是最优的.
针对上述问题,本文采用一种新息协方差估计器对当前时刻k的新息协方差进行估计,通过新息协方差估计值,将新息序列的弱自相关性作为衡量滤波性能的标准,推导出渐消记忆因子.滤波器的收敛性证明见文献[9].
新息序列协方差S0(k)为[10]
S0(k)=E[r(k)rT(k)]=λ(k)HΦP(k|k-1)·
ΦTΗT+ΗΓQ(k-1)ΓTΗT+R(k)
(14)
为满足式(14),此时式中的S0(k)应为实测的新息序列协方差而非理论值,因为一旦S0(k)取理论值,那么式(14)就成为一个恒等式,也就无法求解渐消记忆因子λ(k).由此得到λ(k)的表达式为
R(k))(ΗΦP(k|k-1)ΦTΗT)-1]
(15)
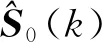
对于新息协方差的估计值,文献[5]采用算数平均法得到k时刻新息协方差的估计值,表达式为
(16)
采用算数平均法的缺点是,只对k时刻之前的新息序列平方和进行算数平均作为k时刻新息协方差的估计值,对新旧数据的利用程度都相同,随着周期的增加,新息协方差的估计精度也会下降[11].为此,本文设计了一种基于指数加权的新息序列协方差估计器.
对于k时刻之前的数据,其加权系数为
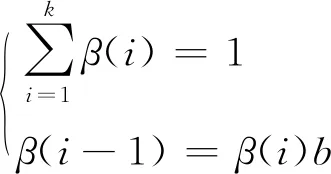
(17)
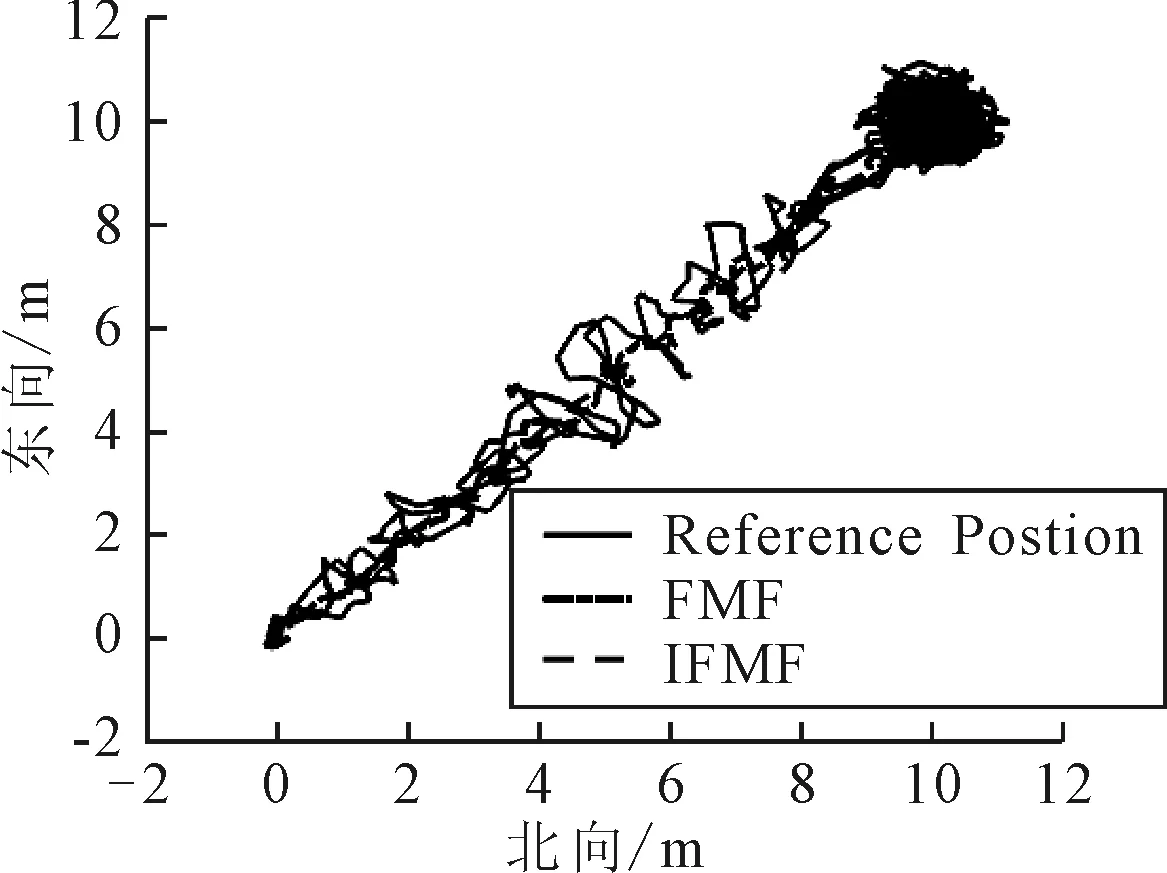
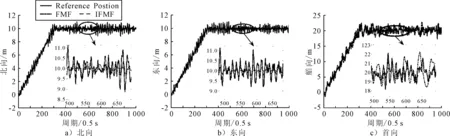
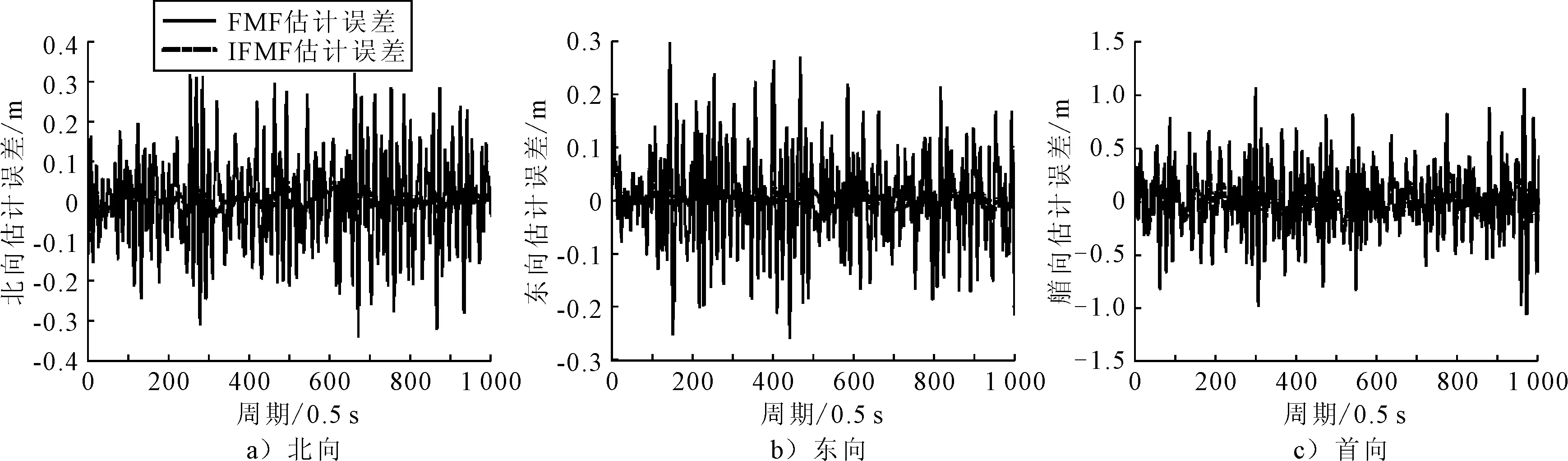
式中:β(i)为第i时刻数据的加权系数;b为衰减因子,满足0 式(17)可以转化为 β(k)bk-1+β(k)bk-2+…+β(k)b+β(k)=1 (18) 在衰减因子b确定之后,β(k)就可以用含b的代数式表达,即 (19) 那么第i时刻数据的加权系数β(i)可表达为 β(i)=β(k)·bk-i (20) β(k)r(i)rT(i)+ (21) 由式(19)可得: (22) (23) 为验证设计的滤波器在鲁棒性和滤波精度方面的性能,以一艘1∶20缩尺比的动力定位平台供应船模为对象对改进后的渐消记忆滤波算法(improved fading memory filter,IFMF)进行仿真,并与文献[6]提出的渐消记忆滤波算法(fading memory filter,FMF)进行滤波结果对比.船模相关参数见表1. 表1 船模主要参数 船舶初始位置设置为[0,0,0],定位点位置设置为[10 m,10 m,20°].采样周期为0.5 s,衰减因子b取为0.95.为模拟实际定位过程,在仿真中加入船位推算模型和控制算法模块,与状态估计模块形成闭环系统. 在状态估计的过程中,系统过程噪声的统计特性主要由高频项、未知环境力项以及模型不确定项共同决定[12],系统真实过程噪声Q为Q=diag(0.1,0.1,0.000 1,0.000 1,0.000 1,0.000 1,0.000 1,0.000 1,0.000 1),为检验噪声统计特性不匹配时两种滤波算法的滤波性能和鲁棒性,在仿真中将系统过程噪声扩大10倍,即Q′=10Q. 仿真结果见图1~3.图1为船舶在水平面内运动轨迹.图2为船舶定位过程中北向、东向和首向参考位置,以及两种方法的估计位置对比.图3为两种方法船舶北向、东向及首向的估计误差对比. 图1 船舶在水平面内的运动轨迹 图2 三种参考位置及两种方法的估计位置对比 图3 两种方法的估计误差对比 由图1可知,FMF和IFMF都能使船舶达到目标位置,但是IFMF使得船舶运动轨迹更加平滑.由图2可知,FMF和IFMF都能有效地估计出船舶的运动状态,但是IFMF的滤波曲线较FMF的滤波曲线更为平滑,这也能一定程度上说明针对系统噪声统计特性不匹配的情况,IFMF的鲁棒性要优于FMF .从横向对比的结果来看,船舶艏向位置的滤波效果较北向和东向相对较差,这是由于艏摇运动的输入为转矩,而纵荡和横荡运动的输入为力,而力矩比力更难执行.由图3可知,IFMF在定点定位过程中的估计误差要明显小于FMF,说明IFMF具有更好的收敛性与抗干扰能力,面对系统过程噪声统计特性不匹配的情况,IFMF能更好地跟踪船舶运动状态,为控制系统提供更精确更平滑的输入,提高动力定位系统整体的稳定性. 文中针对复杂海况下动力定位船舶存在的系统过程噪声统计数据不充分以及常规渐消记忆滤波无法得到最优渐消记忆因子的问题,设计了一种改进的渐消记忆滤波算法.该算法通过设计新息协方差估计器能够为滤波器提供准确的渐消记忆因子,从而达到自适应调整增益矩阵和改善滤波器鲁棒性的目的.仿真实验验证了所设计算法的有效性.
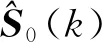
4 仿真结果与分析

5 结 束 语
