混合蚁群算法求解带软时间窗的车辆路径问题

李 卓 李文霞 巨玉祥 陈晓明 何晓平

(兰州交通大学交通运输学院 兰州 730070)

0 引 言

车辆路径问题(vehicle routing problem,VRP)是物流供应链研究领域的经典核心问题[1]，带软时间窗的车辆路径问题(vehicle routing problem with soft time window,VRPSTW)是组合优化中在物资送达各客户点设置了带有惩罚性质的软时间窗约束，是经典VRP中的一种变体，现实中快递配送[2]、应急物资调度[3]、人员救护[4]等路径规划问题均可被归纳为VRPSTW问题.

考虑到VRPSTW问题的NP-hard性质，精确算法在求解具有一定规模的问题时已不适用，而启发式算法在求解大规模VRP问题的适用性凸显，已被学术界广泛认可，且不少学者在传统算法的基础上进行了改进.范厚明等[5]将变领域下降搜索应用于粒子群算法的扰动，提高了算法的搜索性能，并将其应用于求解同时集配车辆路径问题.郭咏梅等[6]针对应急物流背景下的车辆路径问题，将人工鱼群算法中拥挤度因子引入蚁群算法来指导蚁群的聚集，提高了算法性能.值得注意的是，蚁群优化算法在计算复杂性和收敛速度方面比较适用于求解VRP及其变体问题，且解的质量不依赖于解的初始化，具有较好的鲁棒性[7]；然而，由于蚁群算法较强的自组织性和正反馈性，表现出良好收敛性的同时易陷入局部最优，因此，部分学者通过引入领域搜索[8-9]、精英保留策略或混合其他经典启发式算法优势[10-11]来改进蚁群算法.近些年来，随着新兴群智能优化算法的兴起，不少学者考虑将其应用于各自的研究领域[12]，其中萤火虫算法在许多连续型优化问题中表现出较好的性能[13].由于VRP的离散特性，萤火虫编码与解码是关键环节，已有文献考虑到该问题并对算法进行了改进.孙俊成等[14]对解决连续问题的萤火虫算法进行离散化改进，以适应于开放式车辆路径问题的求解.既有研究表明，萤火虫算法全局搜索能力较强，但获得解的质量高度依赖于解的初始化，算法稳健性和收敛性较差.

综合上述蚁群算法和萤火虫算法的优势与不足，为混合算法设计提供了思路.基于此，考虑两种算法的优势互补，将二者结合设计一种混合算法，算法应用于VRPSTW模型的求解，以期保持求解效率的同时提高求解精度.

1 VRPSTW描述和数学模型

1.1 问题描述

基于物流体系中的末端配送，可归结为带软时间窗的车辆路径问题(VRPSTW).具体而言，一个物资调度中心，配有足够数量的同质车辆，路网中有一组客户需求点，每个客户的需求量和服务持续时间必须满足，考虑尽可能满足客户服务时间窗的同时合理规划车辆路径，使总配送成本最小.

需要解决的问题及基本假设：①车辆从物资调度中心出发，服务若干客户需求点后返回调度中心；②每个客户点仅由一辆车访问且只能被访问一次，其需求量不能超过车辆容量；③车辆为相同车型且运输总量不能超出中心容量限制；④每个客户的坐标、需求量和服务持续时间已知，且都有服务时间窗限制.

1.2 数学模型

1.2.1模型参数

运输网络G=(V,A)，主要参数及相关变量见表1.

表1 模型参数及变量

1.2.2模型构建

参照传统车辆路径问题的优化方向，以配送总成本最小为目标，构建带软时间窗的车辆路径优化模型.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Tik+ui+tijk≤Tjk+C(1-xijk),

∀i,j∈V0,k∈K

(8)

xijk∈{0,1},∀i,j∈V,k∈K

(9)

Qk,qi,ui>0,i∈V0,k∈K

(10)

式(1)为最小化配送成本的目标函数；式(2)～(3)为每个客户需求点仅被一辆车服务且仅访问一次；式(4)为子回路消去约束；式(5)为车辆从调度中心出发最终返回调度中心；式(6)为节点平衡约束；式(7)为车辆容量限制；式(8)为车辆从服务上一需求点到访问下一需求点所要满足的时间条件；式(9)～(10)为决策变量和参数约束.

2 求解VRPSTW的混合蚁群算法

VRPSTW问题是经典VRP问题的子问题之一，被认为是NP-hard问题.由于该问题的求解规模较大，精确算法无法解决指数爆炸问题，难以求得最优解.而传统启发式算法求解VRP问题已得到广泛应用，如遗传算法、蚁群算法、禁忌搜索和模拟退火等均表现出良好的求解效果.因此，通过设计改进的启发式算法以求解VRPSTW问题.

2.1 蚁群算法

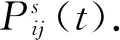
(11)

式中：α为信息素重要度因子；β为启发式信息重要度因子；alloweds=V/{tabus}为蚂蚁s下一步允许访问的节点集合，tabus为蚂蚁s访问过的节点集合，即路径禁忌表.

启发式函数ηij(t)越大，蚂蚁选择节点j的概率越大.随着迭代次数的增加，路径(i,j)的信息素浓度τij不断叠加，同时残留的信息素将持续挥发，则(t+1)时刻路径(i,j)的信息素τij(t+1)浓度更新规则为

(12)

式中：ρ为信息素挥发系数；Q为全局信息素常量；由于模型目标是成本最小，则cost(i,j)为路径(i,j)上的成本.

2.2 萤火虫算法

萤火虫算法(firefly algorithm,FA)将搜索空间的每个可行解模拟为自然界中的萤火虫个体，将迭代搜索过程模拟为萤火虫个体间的吸引和移动过程.其基本原理涉及两个主要因素：种群个体的发光亮度和个体间的相互吸引度.发光亮度与个体的适应值有关，适应值越好，亮度越强；吸引度与发光亮度成正比，与个体间的距离成反比；亮度更高的萤火虫吸引种群中其他个体朝着其搜索领域内更优的位置移动，以此来完成优化过程中萤火虫个体位置的更新.

个体i的发光强度Ii用适应值表示，适应函数一般为目标函数，表示为

Ii=f(Xi),Xi=(xi1,xi2,…,xid)

(14)

若个体i的亮度大于个体j，则萤火虫i对萤火虫j的吸引度βi,j随距离变化

(15)

式中：β0为最大吸引度，即光源处(r=0)；γ为光吸收系数，γ∈[0.01,100]；ri,j为个体i与个体j间的欧式距离.

个体j被个体i吸引，位置更新公式为

Xj(t+1)=Xj(t)+

βi,j(Xi(t)-Xj(t))+α

(16)

式中：α为随机控制参数，α∈[-1,1].

2.3 萤火虫-蚁群混合算法

蚁群算法在VRPSTW问题中得到成功的应用[15]，由于其具有较强的信息反馈机制，对大规模问题具有较高的求解效率，但当迭代后期信息素浓度过高时易产生信息素停滞，导致过早收敛，从而陷入局部最优.针对此问题，考虑萤火虫优化中较劣个体自组织性地向较优个体的移动，促使种群在向优势个体聚集的过程中完成个体位置的迭代更新，在此过程中能搜索到新的解空间.基于此，提出将以上萤火虫个体间的寻优过程引入蚁群优化，综合二者的优势提出萤火虫-蚁群混合算法(ACO_FA)，以期在每次迭代中产生额外的满意解，用来进行蚂蚁信息素扰动，避免信息素的停滞，改善算法过早收敛的情况并跳出局部最优.

算法以蚁群算法为基本框架，将萤火虫个体的寻优过程用于扩大搜索的解空间，通过控制迭代过程中信息素的聚集，提出一种信息素交换过程(以下简称FA搜索过程).算法流程见图1.

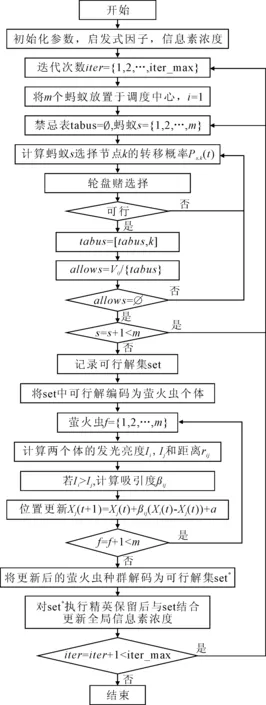
图1 算法流程图

2.3.1FA搜索过程

提出的算法首先调用蚁群算法，构造各次迭代的可行解集，然后调用FA搜索过程，对得到的额外的可行解集进行择优处理后与原可行解集结合，来更新路径上蚂蚁信息素浓度.

由于VRPSTW问题是离散优化问题，而萤火虫算法在求解连续型问题更为适用，因此，为了使萤火虫适应离散优化问题，提出对初始可行解进行重新编码与解码，以此将萤火虫算法应用于离散优化问题中.

1) 萤火虫编码 蚁群算法构造各代的初始可行解s；将整数1～n(n为客户数量)按升序形成序列sq1=(0,1,2，…，n)；将蚁群算法中得到的可行解s与序列sq1一一对应后，sq1按可行解s中客户序号升序排列，得到客户点1～n的访问次序sq2，即编码的萤火虫个体.

2) 位置更新 通过上述编码方式对可行解集进行萤火虫编码，并按式(14)计算各个萤火虫个体的发光强度，例如个体i被编码为216354，个体j被编码为315462，且个体i的亮度大于个体j，计算个体间各元素的距离，见图2，rij=6.按式(15)～(16)进行萤火虫个体各元素位置的更新，形成新的序列sq3，即新的萤火虫个体.

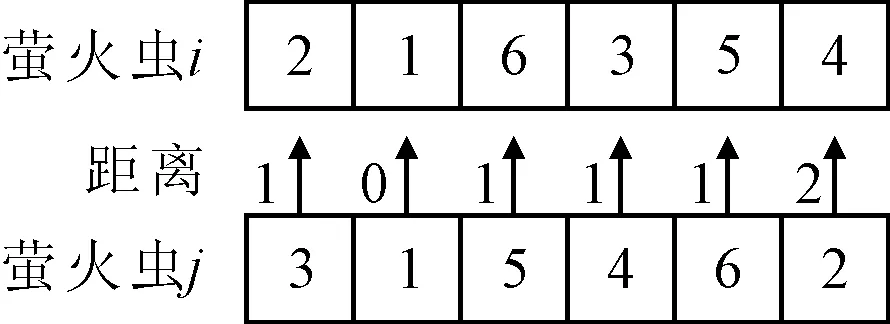
图2 萤火虫个体间的距离

3) 萤火虫解码 更新后，序列sq3可能出现非整数或负数，对其进行合法化处理：序列sq1与sq3一一对应后，序列sq1按序列sq3升序排列得到序列sq*；判断sq*是否可行，即是否满足模型约束，满足，则输出，否则，进行插入1(客户点)操作修复不可行解，以此得到FA搜索后的可行解，见图3.

图3 FA搜索编码与解码

由图3可知，原可行解为261 435，经过FA搜索，更新过的可行解为261 453，在向最优个体移动的过程中，原可行解进行了领域搜索，改善了解的多样性.

2.3.2全局信息素更新

对经过FA搜索后获得的可行解集执行精英保留策略，得到的优势解与原可行解集共同用于更新路径信息素浓度，在弧段上沉积信息素，以指导后来蚂蚁的路径寻找机制.路径(i,j)的信息素浓度τij(t+1)按下式更新：

(17)

(18)

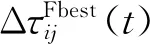
3 算例分析

3.1 实验设置

算例的实验数据通过Matlab随机生成一个配送中心和19个客户点.所有客户点随机分布在(0,70)2的平面坐标内；客户需求是区间[0,20]随机产生的整数(t)，时间窗等其他信息见表2；车辆行驶速度v=2 km/min；单车载重60 t；客户单位需求量的服务时间为1 min/t；单位距离成本为5元/km.提出的算法相关参数见表3.

表2 客户信息表

表3 提出的算法相关参数

3.2 模型计算结果及分析

对于混合蚁群算法的性能，以软时间窗条件下的配送总成本最小化为目标，通过Matlab软件编写程序，在相同的参数设置及实验条件下，分别对传统蚁群算法与文中提出的混合算法进行500次迭代，并针对给定的数值实验分别运行10次程序，统计结果见表4.

所有算法在一台搭载1.6 GHz的Intel Core i5处理器和4 GB内存的计算机平台上实现，算法收敛曲线和模型优化结果见图4～5.

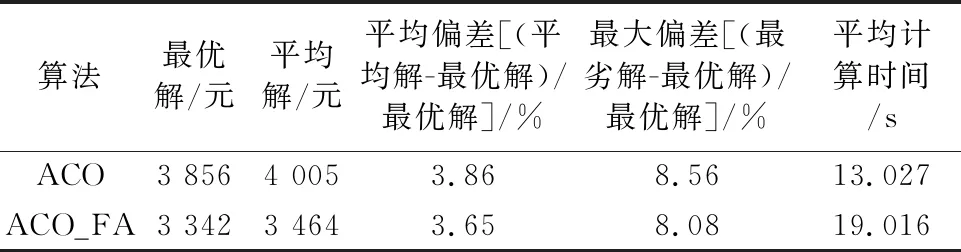
表4 ACO_FA算法与ACO算法数值实验统计结果

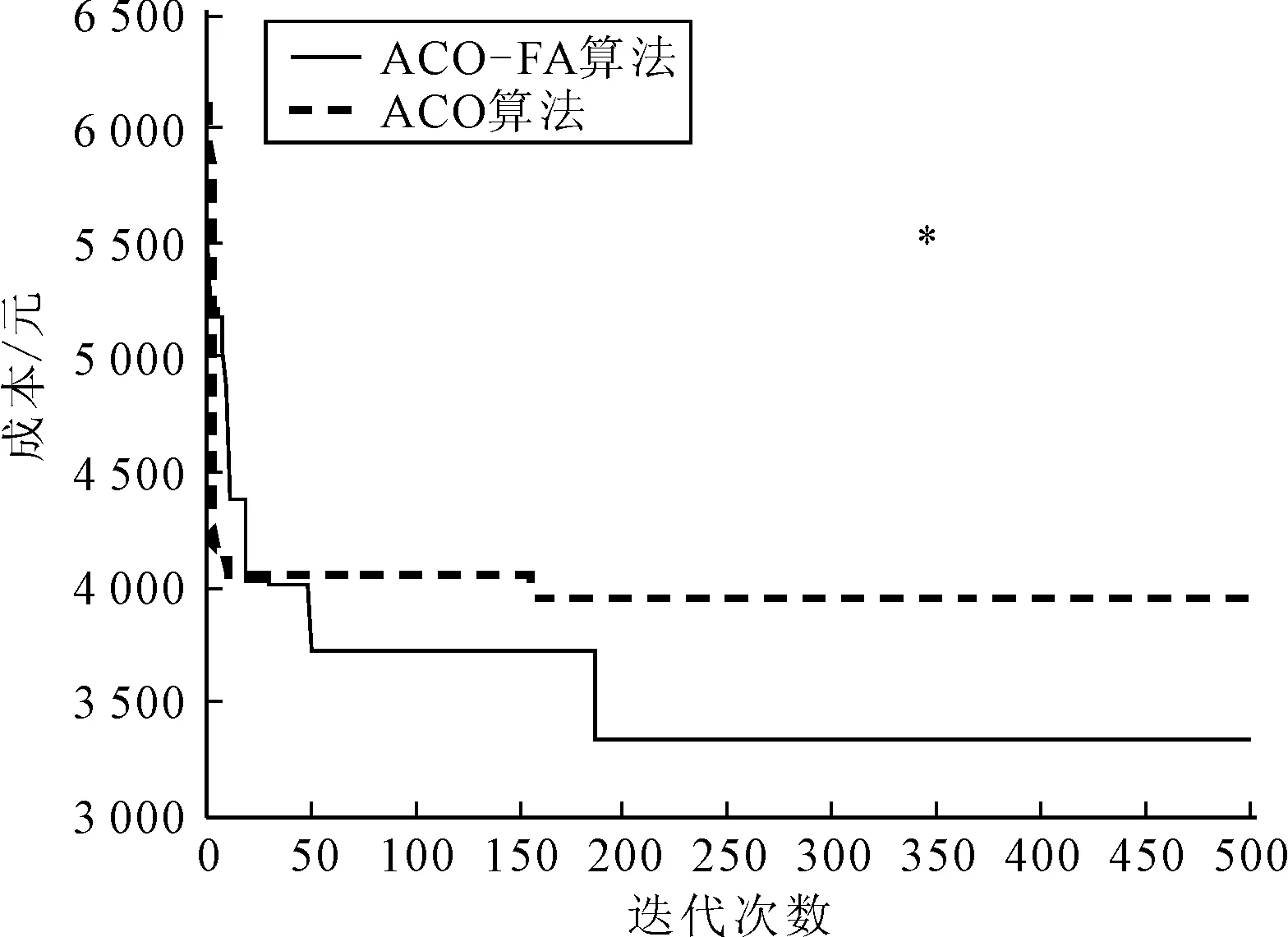
图4 ACO_FA算法与ACO算法收敛曲线对比

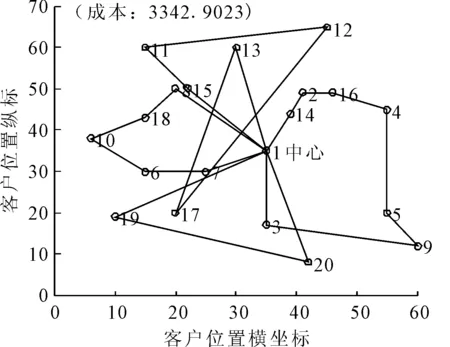
图5 ACO_FA算法优化结果

由表4可知，混合算法相较于传统蚁群算法在解的准确度上有显著提高，全局最优解优化了约15.4%，全局平均解优化了约15.6%，反映出算法在优化过程中解决了蚂蚁信息素停滞的弊端，避免陷入局部最优状态；其次，解的平均偏差降低了约0.21%，最大偏差降低了约0.48%，说明算法在提高最优解质量的同时，对算法的稳健性也有改善，表现出良好的求解性能.由于提出的算法在原有蚁群算法的基础上增加了FA搜索过程，故需要在领域搜索中花费额外的时间，因此，在计算中需要更多的时间.

不同于一般领域搜索的随机性扰动，算法中的FA搜索过程是有方向的领域搜索，是以本次迭代种群中较优解为目标进行扰动，改善每代可行解多样性的同时，使搜索过程更有目的性，加快算法的收敛，以期在保持原有的求解效率的同时提高求解准确度.由图4可知，此算法在迭代177次时达到最优，蚁群算法在迭代158次时达到最优，基本保持了良好的收敛性.

显然，此模型可以有效的解决带软时间窗的车辆路径问题.配送中心在车辆有限载重的条件下，尽可能满足客户时间窗的同时，使总成本最小，配送最低成本为3 342元，配送路径1为1-14-2-16-4-5-9-3-1，车辆满载率为100%；配送路径2为1-7-6-10-18-8-1，车辆满载率为95%；配送路径3为1-15-11-12-17-13-1，车辆满载率为88.33%；配送路径4为1-20-19-1，车辆满载率为43.33%.

4 结 论

1) 考虑到蚁群算法在迭代过程中的信息素停滞问题，将萤火虫算法中萤火虫的寻优机制引入蚁群算法，有目的性的扩大搜索的解空间，保持每代解具有多样性，以此来优化蚂蚁信息素浓度的更新机制，克服了陷入局部最优的瓶颈，最终提高解的精确度，并且在一定程度上保持了原有算法的求解效率.

2) 改进蚁群算法在精确性上有显著提高，在算法稳健性也有较大改进.仅考虑了单目标蚁群算法的性能，设计求解多目标优化问题的蚁群算法将是下一步研究方向.