基于宏观基本图的路网交通拥堵甄别方法研究*

马莹莹 邹祥莉 徐建闽

(华南理工大学土木与交通学院1) 广州 510640) (广州交通信息化建设投资营运有限公司2) 广州 510633)(现代城市交通技术江苏高校协同创新中心3) 南京 210096)

0 引 言

交通状态识别方法主要是基于检测到的现状基础交通数据，采用一些如McMaster算法、加州系列算法、标准偏差(SND)算法、双指数平滑(DES)算法和贝叶斯(Bayes)算法等相关算法来计算得到预先选定的评价指标的现状值，然后通过将现状值与预先设定的状态阈值进行对比，根据现状值所处范围得到相对应的拥堵状态[1-2]；Yaster等[3]提出了利用模糊理论中的模糊逻辑来判断交通拥堵状态，该方法不需要像传统方法一样考虑临界状态阈值的决策问题；Wang等[4]开发一种道路交通状态检测方法，通过安装检测器获得相应的交通数据，然后将获得的数据输进随机宏观交通流模型中，再利用改进的卡尔曼滤波方法来对道路交通拥堵情况进行判别；巫威眺等[5]根据交通流的复杂性，基于对交通状态的定量划分，提出了一种基于BP神经网络的道路交通状态实时判断方法，并利用Matlab软件进行了仿真验证；于荣等[6]提出了基于支持向量机选择车流量、平均速度以及占有率三个评价指标对道路交通拥堵状态进行分类识别，并利用Matlab中的LiBSVM工具包对分类效果进行对比分析；张晓燕等[7]针对城市道路路段常发性拥堵问题，首先分析了常发性拥堵产生的时空特性，然后确定了三级拥堵评价指标，分别是拥堵阈值、拥堵时长比和拥堵常发频度，基于此构建了一个平台实现对常发性拥堵的时空分布进行筛选，并运用GIS技术，达到高效识别城市常发性拥堵路段的目的；李佳等[8]基于图像抓拍技术提出一种基于图形图像的交通拥堵识别方法，并通过建立交通状态综合评价指标(如交通流量、占有率等)，再对抓拍的实时数据图像进行相关处理，实现对道路路段拥堵状态的判别；叶卿[9]针对信号控制交叉口的拥堵识别问题，以交通流量，交叉口排队长度和占有率为评价指标，提出一种基于朴素贝叶斯决策的交叉口交通拥堵判别方法，该方法主要通过贝叶斯分类器对实时采集的交叉口交通数据进行分类，从而识别交叉口的交通状态.

综上所述，目前的交通拥堵状态识别技术存在以下几点不足：①交通拥堵状态判断主要是针对交叉口或者道路路段，反映的是交叉口或者路段的拥堵情况，不足以代表整个路网的交通状况；②交通状态等级的划分缺乏系统性，仅仅作了简单的统计和平均，难以反映各个交叉口、路段之间的关联性和整体性；③目前拥堵状态评价指标大多采用速度、占有率、饱和度等需要经过计算处理的指标，其获取过程复杂，不能达到快速甄别的效果且可靠性降低.基于此，本文提出一种基于宏观基本图的路网交通拥堵甄别方法，能够弥补现有交通状态判别法在路网方面应用的局限性，同时加快了拥堵甄别的速度，达到了交通状态判别的实时性.

1 宏观基本图绘制

1.1 交通小区划分

进行交通小区划分，首先要确定交通小区基本特征边界值，包括小区面积的最大值与最小值、小区内交叉口数目等；然后可以由专业技术人员根据交通小区特征要求和经验进行划分，也可以应用其他软件进行辅助划分.为了进一步与交通管理和控制衔接，交通小区需具备以下特征：①小区内部交叉口应该互为连通；②小区外形应为凸，不应出现内嵌的情况；③小区内交叉口应具有较大的交通关联性.

1.2 宏观基本图绘制

宏观基本图为交通小区内车辆数与驶出交通小区的车辆数的关系图，图中横坐标表示交通小区内车辆数，纵坐标表示驶出交通小区的车辆数，此关系图会呈现较为明显的三段变化趋势，当交通小区内车辆数较少时，随着驶入交通小区车辆数的增加，驶出交通小区的车辆数随之增加，呈现上升趋势；当驶入交通小区的车辆数增加到一定值，驶出交通小区的车辆数在小范围内维持在最大值上，呈现水平趋势；当驶入交通小区车辆数继续增加到一定值，驶出交通小区的车辆数开始逐渐减少，呈现下降趋势.通过各交通小区的检测数据，经过变换同时可以绘制出整个路网以及其他不同范围大小网络的宏观基本图，如果实地检测器数据无法覆盖宏观基本图的三段变化趋势，可以通过路网交通仿真补充相应数据.

2 基于宏观基本图的路网交通拥堵甄别方法

2.1 临界点及其附近范围的确定

绘制出各交通小区及整个路网的宏观基本图后，如何快速地找到图形不同变化趋势的临界点并准确判断交通拥堵状态是关键.使用数据统计软件对已获得的宏观基本图进行曲线拟合，绘制光滑的拟合曲线并得到曲线方程y=f(x)，根据函数性质，通过对曲线方程求一阶导数函数y′=f′(x)，分析曲线变化趋势，得出曲率变化的转折点.根据宏观基本图的三段特性，由于-0.05≤y′=f′(x)≤0.05时，曲率变化非常小，可近似为水平段，那么y′=f′(x)≥0.05为曲线上升段，y′=f′(x)≤-0.05为曲线下降段，通过方程求解可得到曲线趋势变化的临界值分别为x1和x2.由于临界点附近的交通状态是不稳定的，它不仅跟路网内剩余车辆数有关，还跟上一时刻路网的交通状态有关，因此本文提出不同情况下的不同路网拥堵状态甄别方法，假设当路网内车辆数为x1、x2处是不同拥堵状态的临界点，则围合临界点x1的附近范围是(x1-Δx,x1+Δx)，围合临界点x2的附近范围是(x2-Δx,x2+Δx)，当路网内车辆数不在临界点附近范围内时，根据宏观基本图状态划分直接判断拥堵状态；当路网内车辆数处于临界点附近范围内时，提出基于马尔科夫链模型的判断方法.

2.2 临界点附近范围外的拥堵状态判断

根据宏观基本图的三段变化趋势，将交通拥堵状态分为三个等级，并通过路网内车辆数来进行状态甄别，假设t时段检测到的路网车辆数为nt，且nt不属于临界点附近范围，那么t时段路网拥堵等级L的判断方法为

(1)

2.3 临界点附近范围内的拥堵状态判断

当路网内车辆数处于临界点附近范围内时，建立基于马尔科夫链模型的拥堵状态判别方法.

1) 状态划分t+1时段变化率为

(2)

式中：yt为t时段驶出路网车辆数；yt+1为t+1时段驶出路网车辆数；xt为t时段路网内车辆数；xt+1为t+1时段路网内车辆数.

当变化率为-0.05≤Kt+1≤0.05时，可认为变化非常小，接近水平段，因此,以Kt+1=0.05和Kt+1=-0.05为临界点将变化率分为三个状态：畅行状态、轻微拥堵状态和严重拥堵状态.

2) 建立状态转移概率矩阵

P=[Pij]n×n是系统的状态转移矩阵，其中Pij为系统在t时刻处于状态i，在下一时刻t+1处于状态j的概率;n为系统所有可能的状态的个数.基于拥堵状态转移的特殊性，用0-1整数表示转移概率，即

因此，拥堵状态转移矩阵可表示为

3) 判断状态 通过状态划分和状态转移矩阵的确定，可对宏观基本图中转折点附近范围内的交通状态进行判断，判断法则见表1.

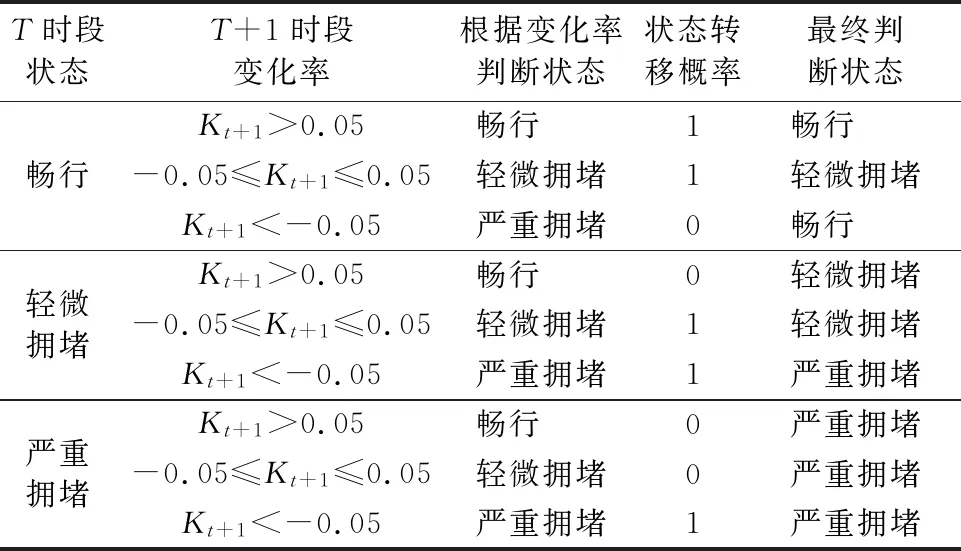
表1 基于马尔科夫链模型的拥堵状态判别方法

3 案例分析

图1为示例路网，该路网东西向长度3 000余m，南北向长度2 000余m，共有十字交叉口16个，丁字交叉口两个，五路交叉口两个.路段为单向2车道，交叉口拓宽为3车道.

1) 交通小区划分 路网共包含交叉口20个，划分成四个交通小区，每个交通小区包含交叉口个数为4～6个，基于交通小区的特性，根据该路网的路径选择、交叉口及路段的物理关联性大小，采用手动划分的方式得到各交通小区见图2.

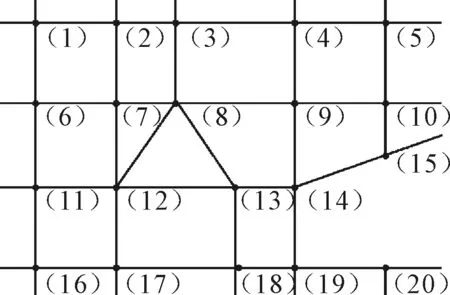
图1 示例路网

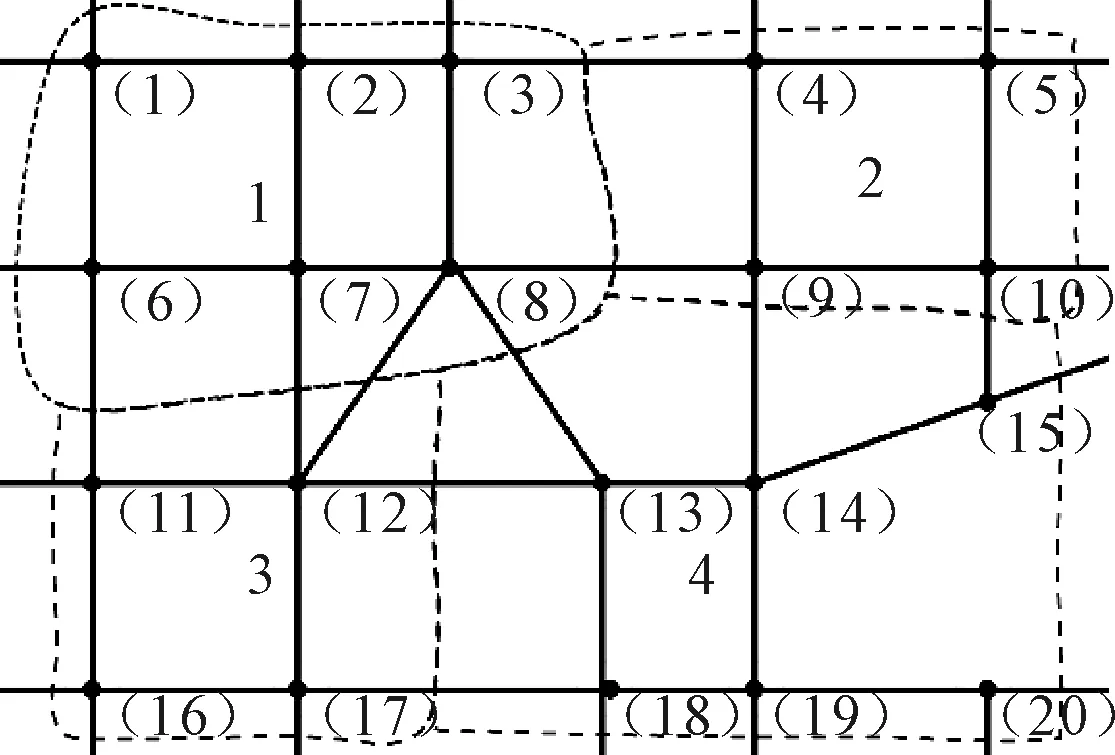
图2 交通小区划分

2) 宏观基本图绘制 利用VISSIM仿真软件建立图1的路网，十字交叉口为四相位控制，丁字交叉口为三相位控制，五路交叉口为五相位控制.并在各路段设置出入口，车辆通过出入口进入网络或到达终点，在各进出口道设置检测器，记录t时段驶入各交通小区以及驶出各交通小区的车辆数nt，仿真时长为12 000 s，每60 s记录一次数据.

(3)

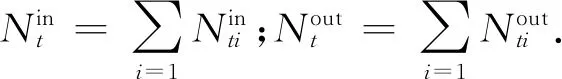
运用以上公式获得单位时间驶出各小区的车辆数以及各小区内车辆数，绘制得到各个交通小区和总路网的宏观基本图，综合考虑计算复杂性和拟合度，采用三次函数进行曲线拟合，得到图形和拟合函数见图3.

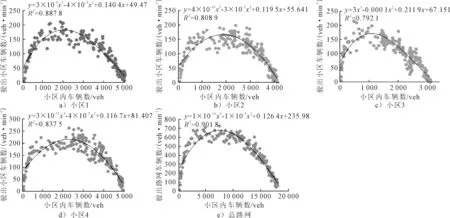
图3 宏观基本图及拟合曲线方程

3) 拥堵状态判断 通过步骤2获得了各交通小区及路网的宏观基本图的拟合曲线方程，对各方程进行一阶求导得到一阶函数y′=f′(x)，并令y′=f′(x)=0.05和y′=f′(x)=-0.05，求得各个小区的临界点，见表2.

表2 状态划分临界点 veh

对于小区1和小区3，由于y′=f′(x)=-0.05无解，可尝试求解y′=f′(x)更趋近于0的解，例如小区1可求得y′=f′(x)=-0.03时的解为5 350、3 539，可取临界点为(1 329，3 539)；而小区3由于y′=f′(x)=0也无解，因此取临界点为(1 385，1 949).

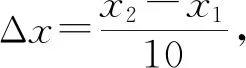
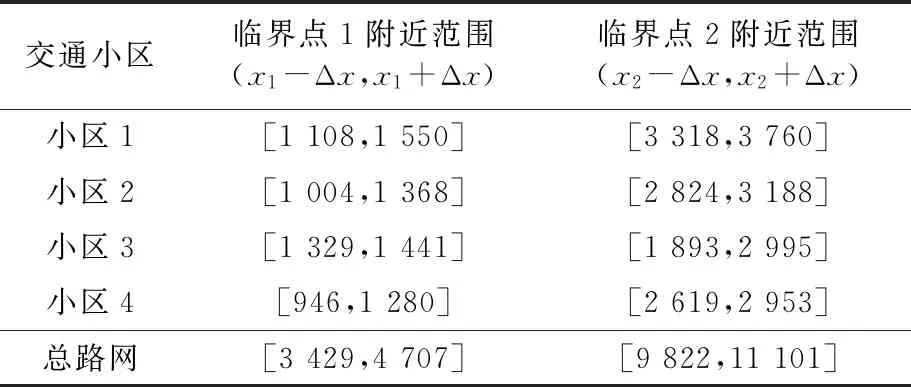
表3 临界点附近范围 veh

通过小区(路网)内车辆数来进行状态甄别，假设t时段检测到的小区(路网)内车辆数为nt，若nt在临界点附近范围外，那么t时段小区(路网)拥堵等级L的判断方法为

对于小区1：

对于小区2：

对于小区3：

对于小区4：

对于总路网：

若nt在临界点附近范围内，则采用基于马尔科夫链模型的判别方法.

例如从仿真结果中获得t时段各交通小区(路网)内车辆数及驶出车辆数数据见表4.

表4 t时段各交通小区相关数据 veh

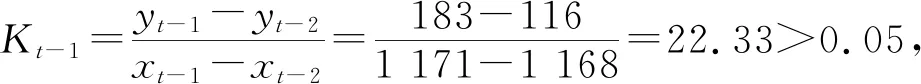
对于总路网，由于4 068<5 586<10 462且5 586∉[3 429,4 707]，因此,总路网为轻微拥堵状态.

4 结 束 语

本文通过交通小区划分、绘制宏观基本图、界定拥堵临界点、判断拥堵状态以及拥堵状态的输出等一系列步骤建立了基于宏观基本图的路网拥堵甄别方法，并结合了马尔科夫链模型，使临界点附近的状态判别更加精准.该方法的优点主要有以下几点：①该方法既可以甄别网络整体的拥堵状态，也可以输出各个小区的交通拥堵状态；②由于临界点附近范围的状态不稳定，该方法通过结合马尔科夫链模型，使状态判别与上一时刻的状态相关，大大提高了判断的准确性；③该方法可通过小区合并和拆分获得不同范围的交通拥堵情况，在交通管理和控制方面应用范围较广.未来可基于宏观拥堵状态判断进行微观交通拥堵疏解控制方面的研究.