叶轮机械全环非定常大规模并行模拟程序设计

张 健唐 静邱 名邓有奇龚小权

(中国空气动力研究与发展中心 计算空气动力研究所,绵阳 621000)

0 引 言

叶轮机械内部流动非常复杂,其本质为三维黏性非定常流动。计算流体力学(Computational Fluid Dynamics,CFD)技术飞速发展,其具备计算耗时短,成本相对较低,并且可以多维度地模拟出叶轮机内部复杂的非定常流动细节的优点,因而越来越多地用于叶轮机械的气动设计和分析当中。

叶轮机内部非定常流动的来源有多种,动静叶片排的相对转动、激波边界层干扰、尾迹传播、二次流等都是造成流动不稳定的原因。通过数值模拟对上述非定常现象进行研究的关键在于如何建立模拟转静叶片相对运动过程的模型。目前工业上一般采用混合平面(Mixing Plane)模型[1],该模型将转/静界面上下游相同展向高度处的通量通过周向平均后进行交换,将非定常计算简化为对一个叶片流道的定常计算,虽然大大减小了计算量,然而却无法捕捉到转静子之间相互干扰等非定常现象。采用叶片约化技术[2],将叶片在周向方向上按照一定比例进行几何缩放,能够使转静叶片数具有较大公约数进而约化为少量几个叶片通道进行非定常计算,但是由于改变了实际的几何尺寸,这种方法会存在较大误差。He和Ning提出的非线性谐波法(Non-linear Harmonic Method,NLH)[3]可以看作是一种定常/非定常混合方法,其基本假设是流场的主要扰动是由于叶片通过频率(Blade Passing Frequence,BPF)引起的,从而将流场变量分解成为时间平均值和多个不同频率谐波的扰动组成,BPF的整数倍数分别代表了不同谐波。为了得到最终的流场解,除了要求解时间平均方程外,还需要求解各个不同频率的谐波方程。NLH模型优点是在计算消耗可承受状态下得到相对精确的非定常流场,但缺点是需要预先给定频率,对于未知频率流动和多频率的组合模拟存在困难,特别是旋转失速等非定常流动,NLH不可能解决。而且,随着频率数目增加,NLH的求解量也会剧增。在未来的航空发动机设计流程中,全环非定常数值模拟多级压气机/涡轮内部的复杂三维流动必然会成为一种趋势和常规手段。NASA支持开发的流场求解器TURBO[4]就是一个精确模拟三维非定常发动机流场的软件。Chen等利用TURBO全环数值模拟了压气机失速开始状态的流场,并研究了相关的失速控制技术[5]。北航邵飞等利用商用软件CFX全环计算了某高压涡轮非定常流动,捕捉到了流场中存在的低频扰动[6]。

由于计算量巨大,展开叶轮机械全环非定常研究具有较大挑战性。随着高性能计算机的飞速发展,计算机硬件逐渐不再是限制CFD计算的主要因素。我国的神威太湖之光[7]、天河二号[8]等超级计算机已经达到了每秒亿亿次量级的浮点数计算能力。数千万甚至上亿网格量的计算已不再是难题。美国NASA关于2030年CFD发展展望的报告[9]中,多次强调了高性能计算(HPC)在未来叶轮设计的重要作用。基于此,本文提出了一个大规模并行模拟程序设计策略,并针对叶轮机械的三维非定常流动进行了全环数值模拟,从而对更加深入研究发动机内部复杂流动机理提供保障和基础。

本文依托气动中心千万亿次高性能计算集群,在自主研发的三维混合网格流场求解器MFlow[10]的基础上,开发构建了叶轮机定常模块、非定常流动数值模拟模块。滑移网格及通量守恒插值模块的研发实现了航发叶轮机的全环非定常模拟。研究先通过一个典型单级压气机进行了程序的验证与确认,然后利用1.5级涡轮算例进行了程序并行效率的测试,最后对一个3.5级压气机超大规模算例进行了尝试,分析了动静叶片相互干扰过程,评估了程序对于大规模复杂工程应用的适用能力。

1 计算方法模型

1.1 控制方程

流场求解采用三维非定常雷诺平均Navier-Stokes方程(URANS)在旋转坐标系下的形式:

式中:Ω为控制体单元；S代表单元面。U为守恒变量,F I和F V分别是无黏通量和黏性通量,S T为科里奥利力和离心力引起的源项,具体形式如下:

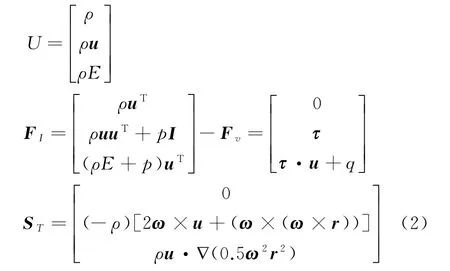
式中:ρ为密度,u为相对速度矢量,E为总能,p为压力,q为热通量,τ为剪切应力张量,ω为旋转角速度,r为径向矢量。

1.2 数值方法

对于方程式(1),时间推进采用双重时间步法,外迭代采用欧拉后插显式推进,每一个时间步子迭代利用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法[11]隐式迭代。空间离散基于控制体的有限体积法,采用Roe迎风格式[12]计算无黏通量,利用格林-高斯公式计算控制体单元的梯度,选择Venkataknshnan限制器[13]将控制体的原始变量通过线性重构插值到控制体单元面左右,达到更高的空间精度。采用中心格式计算黏性通量,湍流模型选取Spalart-Allmaras(SA)一方程模型[14]。

1.3 边界条件

对于进口边界,给定总温T0,总压p0以及来流速度方向。向外发出的黎曼不变量R－由第一个内部边界点外插计算得到,利用R－计算出绝对速度大小V,再根据速度方向将V分解为各个速度分量。

式中:v d代表边界内部第一个单元速度矢量,c d为当地声速,γ为比热比,n为法向量,C p为定压比热。密度ρ和压力p利用T0、p0、V之间的代数关系以及等熵关系计算得到。

对于内流出口,给定静压,其他变量外插得到。同时引入径向平衡方程式(5),通过给定展向高度r处的静压,其他位置的静压根据密度ρ和周向速度vθ积分得到。

对于黏性物面,为绝热壁,采用无滑移边界条件。对于转静交界面,在每一个物理时间步,上下游的守恒变量随着网格滑移动态完成交换。动静叶排之间利用滑移网格进行耦合,通过将对向网格的守恒变量插值到本方虚拟网格上完成边界条件的更新,如图1所示。

图1 滑移网格技术Fig.1 Sliding interface technique

被插值单元的值通过包裹单元的节点值进行反距离权插值平均方法得到。如式(6)所示,ωi,j为距离权重,d i,j为两点距离。

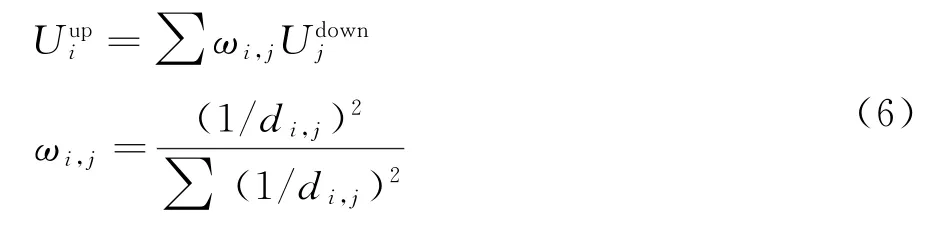
2 并行程序设计

2.1 并行程序框架

图2给出了整个程序的流程图,在每一个非定常时间步完成方程求解、网格旋转、建立映射关系的迭代循环,在每一个子迭代需要完成并行网格分区之间以及转/静界面之间的数据交换。

图2 并行程序框架Fig.2 Parallel program frame

并行区域的划分是在前处理过程中完成的,分区完成后,程序将记录下各个分区的几何信息,同时记录下并行左右分区的映射关系。转/静界面的映射关系是在每一个非定常步求解开始之前完成。数据的并行传值利用消息传递接口(Message Passing Interface,MPI)实现。利用MPI_Comm_Split方法将不同叶片排分区网格分到不同的子通信域,子通信域内完成常规并行边界的通量传递,子通信域之间完成滑移边界的变量插值与传递。

2.2 并行网格分区

并行网格分区利用图切分软件包METIS完成,METIS是由美国密西根大学G.Karypis和V.Kumar编写的用于图的分区和稀疏矩阵排序的串行包,提供k路多层划分算法对混合网格进行分区[15]。给定包含n个节点V和m个边E的图G＝(V,E),将V划分到k个子集中V＝[V1,V2,...,V k],使得|V i|≈n/k,且相连顶点属于不同子集的边的数量要最小化。

图3给出了k路多层划分过程,整个划分过程分成coarsening,initial partitioning和uncoarsening三个部分。coarsening将图的大小逐渐缩小,G1-＞G2-＞G3-＞G4。在G4阶段执行k路划分,然后在uncoarsening阶段将图中的原始节点映射到G4划分的子集中。由于本文采用格心格式的有限体积法,图定义中的节点和边分别指网格中的网格单元和网格面。采用k路多层图划分,保证了各个子区域的总网格数比较均衡的同时尽量减少了分区的边切割,达到了负载均衡目的同时,最大限度减少了分区间的数据通信量。

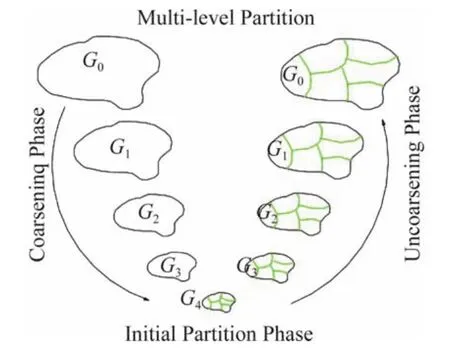
图3 METIS的k路多层图划分过程Fig.3 Multilevel k-way partitioning of METIS

2.3 分区间数据交换

本文并行算法基于分布式大规模并行计算机系统,采用所有CPU都参与迭代计算的对等并行模式,MPI数据传递采用非阻塞通信,尽量加大计算和通信的重叠,每个分区网格只保存必需的局部网格数据和并行分区边界上网格单元及顶点的对应关系。多级叶轮网格内部有两种并行边界,一种是同一叶片排内部,在采用METIS并行网格分区时形成的交界面,另一种是不同叶片排之间的滑移网格交界面。对于前者,并行边界面左右网格的对应关系在前处理分区时就已经确定,所以只需要计算一次并记录下来,以空间换时间,提高并行效率。对于后者,每一非定常步转子叶片网格将进行旋转,滑移边界左右的对接信息发生更新,需要重新计算。插值网格之间的映射关系通过ADT(Alternating Digital Tree)方法[16]建立,该方法将空间单元进行有序排序后,构建为二叉树数据,以便待插值点快速搜索查找[17],减少计算时间。

程序中,对于每一个分区所在的进程中,将该进程的并行边界左右单元(物理单元以及虚拟单元)编号按照向相邻分区发送和从相邻分区接收的顺序连续存储在数组内存中(图4),交换数据时只需要将相应数据按照单元编号存入或取出,并调用MPI数据传递接口完成。

图4 交换数据存储结构Fig.4 Transfer data's storage structure

3 单级压气机算例验证

NASA Stage 35作为典型跨声速压气机常用于压气机内流数值模拟验证。表1列出了Stage 35的具体的设计参数。Stage 35在设计转速17188.7 rpm、流量20.2 kg/s下产生1.8的总压比,Reid和Moore早期对其做过试验,可以得到详细的几何参数、工作条件和试验数据[18]。本文对Stage 35算例分别利用混合平面法进行了单通道定常计算[19]、利用非线性谐波方法进行了“准”非定常计算、利用滑移面法进行了360°全环非定常计算,其中非线性谐波法是通过商用软件Numeca完成的,因为只有一组转静干扰,所以周期性扰动个数设为1,每个扰动采用的谐波数为3个。最后将计算结果同试验数据以及NASA TURBO软件计算的360°全环非定常数据进行了对比分析。

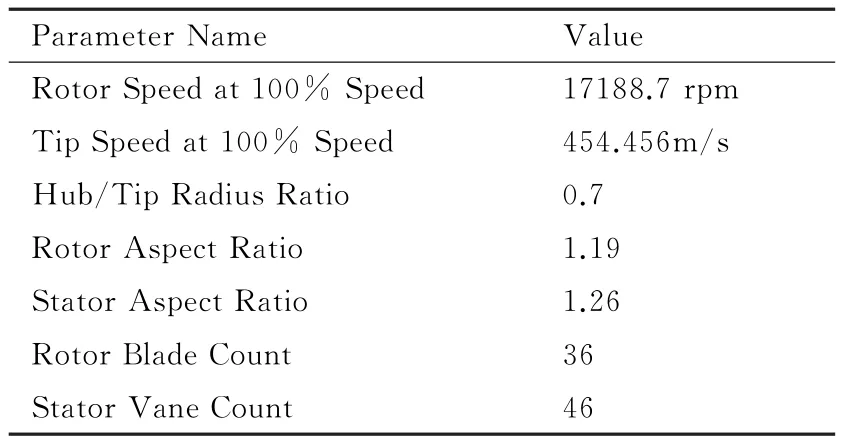
表1 Stage 35设计参数Table 1 Design parameters of Stage 35

本次计算的网格如图5所示,首先完成单通道的网格生成,第一层网格间距3×10-6m,y＋取1,同时考虑了叶尖间隙的影响,间隙展向分布了17个网格点。然后旋转复制得到Stage 35全环网格。总网格量大概在3300万左右。

本次的计算在中国空气动力研究与发展中心的千万亿次集群上完成。并行计算采用512个核,集群芯片的处理器为国产的飞腾FT-1500A处理器,主频2 GHz。每个时间步叶片旋转1°,总共完整计算3圈。图6给出了计算稳定后某一时刻50%叶高全环剖面的压力分布云图。

为了获取压气机的整体性能并且评估数值模拟的精度,图7和图8分别给出了压气机在100%转速下不同方法和模型计算得到的总压比和绝热效率随流量变化的特性曲线,同时给出试验数据进行对比。从图看出,数值模拟得到的压气机整体性能和试验数据吻合良好。相比较而言,本文的全环非定常计算的总压比相对于文献[20]中TURBO软件全环的计算结果与试验数据更加接近,尤其是在接近阻塞(试验中的4004工况)时。本文计算得到最大流量与Reid和Moore试验数据非常接近,表2给出了该状态下的总压比、总温比和绝热效率与试验及TURBO计算结果的对比。可以看到MFlow的计算结果与试验的误差基本都在Reid和Moore提出的试验不确定度范围之内。文献中没有给出TURBO计算的绝热效率特性曲线,相比于混合平面法和非线性谐波法,MFlow全环非定常计算的绝热效率与试验更加接近。在小流量工况下计算得到的压比相对混合面法和NLH低,其原因可能上下游网格信息传递时由于插值精度不够,导致数值耗散大[21]。从整体性能来看,本文程序的计算结果具有较高精度,满足工程应用需求。

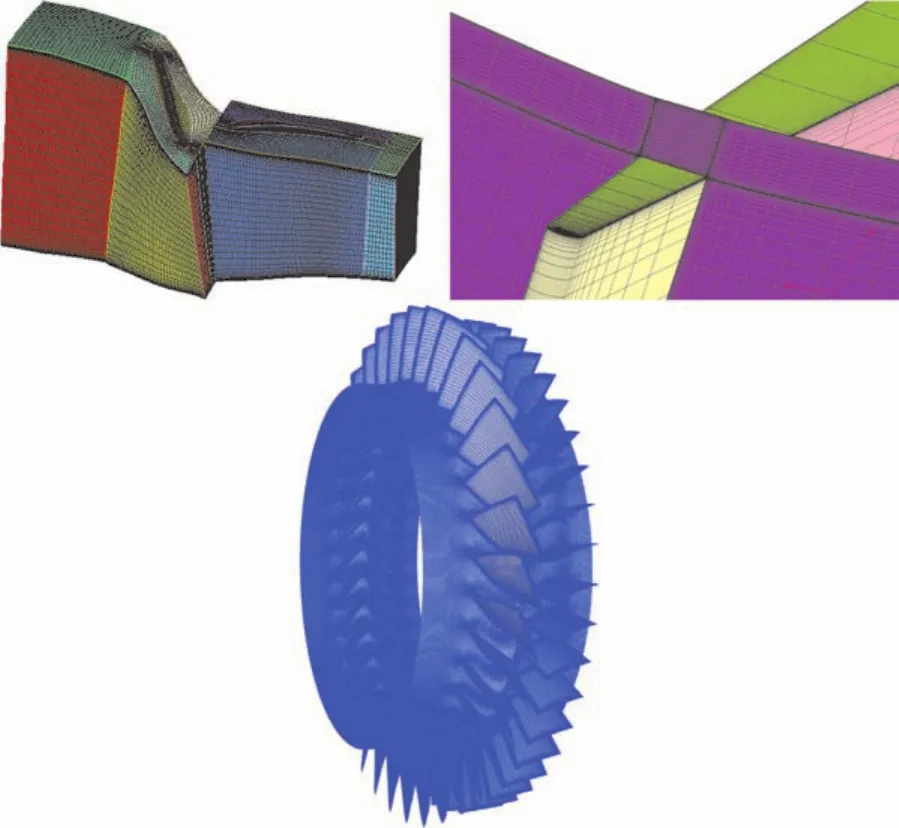
图5 Stage 35计算网格Fig.5 Computational grid of Stage 35

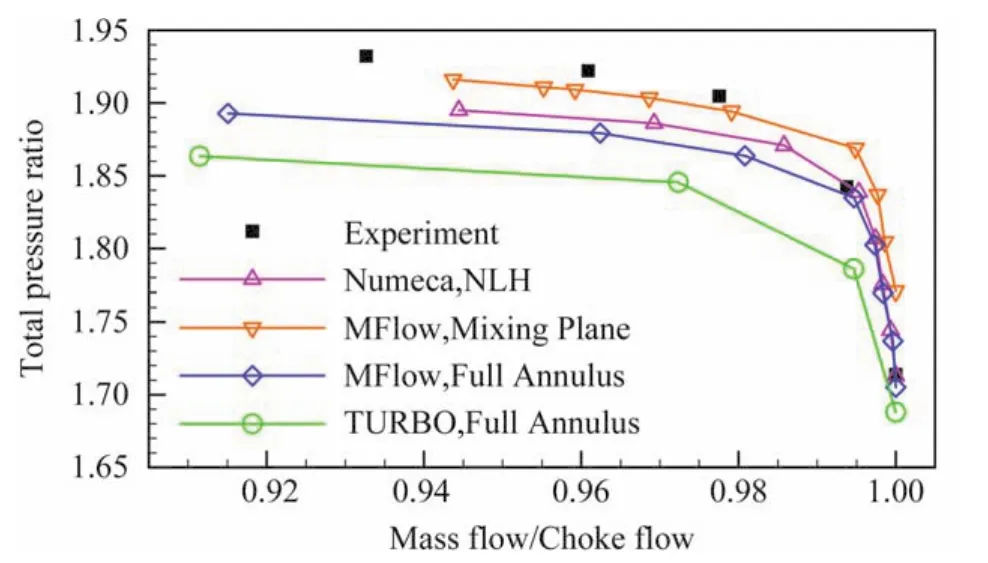
图7 Stage 35总压特性曲线Fig.7 Total pressure ratio of Stage 35

图8 Stage 35绝热效率特性曲线Fig.8 Adiabatic efficiency of Stage 35

表2 Stage 35接近阻塞状态气动特性对比Table 2 Aerodynamic performance of Stage 35 near choke

图9和图10分别给出了利用不同模型计算得到的50%叶高切面压力分布以及熵值云图。通过对比可以看到不同模型计算得到的波系结构基本一致,但是混合平面法由于在转/静交界面进行了周向平均,所以压力和熵值并不连续,尤其是熵增有一个很明显的阶跃。NLH方法的结果与非定常模拟的结果更加接近,能够捕捉到转/静干扰现象。但是仔细观察转子产生的熵值进入静子区域,在几条高亮的尾迹中间还有两条强度较小的尾迹。这是因为NLH方法是通过有限的几个频率谐波方程的定常解合成一个近似的非定常解,不同频率会带来不同波长和幅值的正弦振荡,只有在谐波数足够多的情况下才能完全消除扰动[22]。相比之下全环模拟的结果与实际物理现象更加接近。

图9 不同方法计算压力云图比较Fig.9 Static pressure comparison of different methods

图10 不同方法计算熵值云图比较Fig.10 Entropy comparison of different methods

为研究相邻叶片排之间的周期性干扰过程,在计算过程中对静子尾迹接近出口某处设置一个压力探测点,压力随时间周期变化结果如图11所示,可以看到监测点的静压在一个周期后呈现出良好的周期性,说明非定常计算已经达到稳定。对其进行频谱分析结果如图12所示,可以看到计算很好的捕捉到了叶片通过频率(BPF)及其谐波。

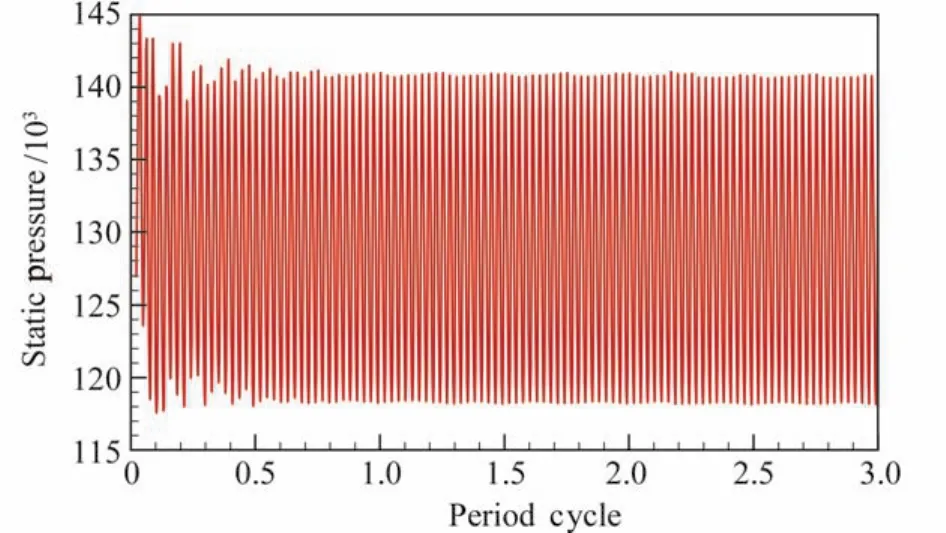
图11 探测点压力变化曲线Fig.11 Static pressure at the probe

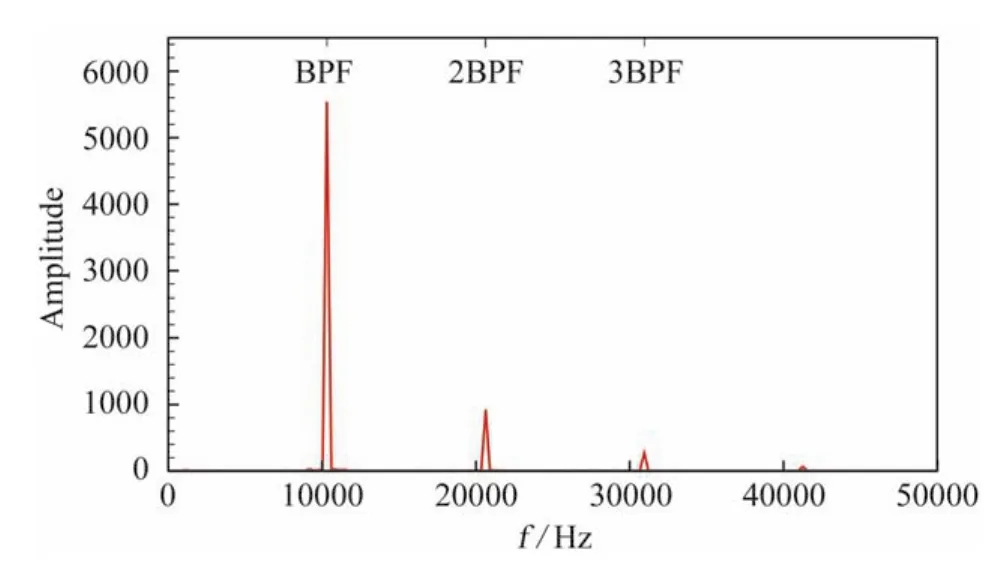
图12 探测点压力频谱分析结果Fig.12 Pressure spectrum

4 并行效率测试

为测试程序的并行计算效率,同时进一步检验程序对不同种类叶轮机械模拟的适应性,本节采用了一个稍大网格规模的1.5级涡轮算例进行了计算和分析。其基本几何构型如图13所示,全环转子叶片共41个,转速3500 rpm,静子叶片36个[23]。图14给出了计算所采用的其中一个叶片通道网格,整个3排叶片全环网格量共计约4000万。

图13 Aachen 1.5级涡轮几何参数Fig.13 Geometry parameters of Aachen 1.5 turbine stage

图14 Aachen 1.5级涡轮计算网格Fig.14 Computational grid of Aachen 1.5 turbine stage

计算不考虑涡轮的传热过程,每一个非定常步转子大约转动1度,每一个非定常步下子迭代200次。对同一状态分别利用180、360、720以及1440个CPU核心数分别计算,从而进行并行效率的测试。图15给出了50%展向环面的熵值云图计算结果,反映了非定常流动损失的输运过程。第一排静叶产生熵的尾迹,遇到转子叶片前缘被切断后转向进入转子叶片通道并向下游传输,再与转子叶片尾迹产生的熵混合,一起进入下游的第二排静叶通道混合。从熵增的流动过程和在转/静界面的连续性来看,计算结果合理。图16是利用不同CPU核数进行了一定步数非定常计算后残差随时间收敛曲线对比,可以明显看到随核数成倍增加,收敛时间几乎成倍减少。图17进一步给出了加速比曲线,可以看到720核时并行效率有90%,1440核并行效率依然能够接近80%。利用1440核完成本算例一个状态的计算,转子完整旋转一周计算时间不到24小时,显示出程序具有较高的并行效率和加速比。

图15 50%叶高环面熵值云图Fig.15 Entropy contours at 50%span annulus

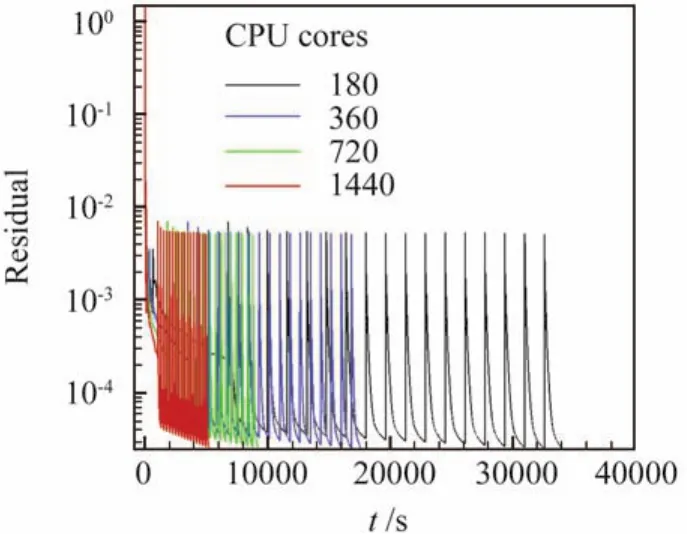
图16 不同核数计算残差随时间收敛曲线Fig.16 Residual convergence using different number of cores

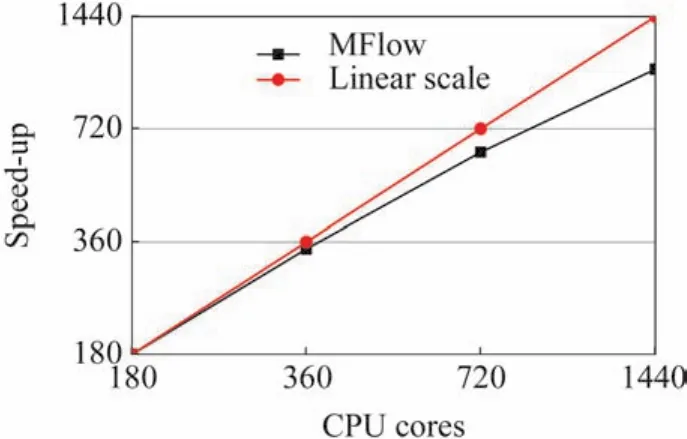
图17 并行效率测试结果Fig.17 Parallel efficiency

5 超大规模算例

在完成程序的验证与确认及性能分析后,利用程序对一个超大规模算例进行了尝试。该算例是某压气机的前3.5级,设计转速15000 rpm。图18给出了本次计算所用的网格,网格总量接近2亿,共分4096个核进行计算。

图18 3.5级压气机全环网格Fig.18 Full annulus grid of 3.5 stage compressor

表3给出了在接近设计点的一个状态下,分别利用混合平面法和全环非定常方法计算得到的压气机气动性能对比。可以看到,由于混合平面法方法模型本身的缺陷,进出口流量误差随着级数的增多累积明显,达到2.5%,而全环非定常的差别只有0.7%,其中可能是插值的精度损失造成的。除流量外,定常模型计算得到的总压比、绝热效率与非定常比差别较明显,说明当压气机级数越多,定常模型计算结果的可信度就越低。

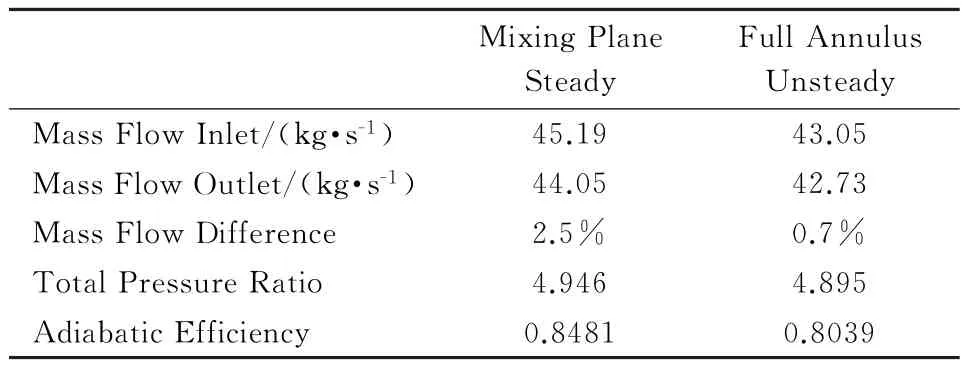
表3 3.5级压气机设计点计算结果Table3 Aerodynamic performance of 3.5 stage compressor at design point

图19给出了计算得到的整机压力分布云图,图20给出了三个不同时刻在前两级叶片排在70%叶高切面的焓值局部放大云图,可以帮助分析压气机内部复杂的动静干扰过程。可以看到,转子叶栅外伸激波会射入上游静子叶栅通道,外伸激波在压力面干扰强、传播速度快、并形成反射,从而使得静叶压力面的附面层快速增厚,静叶表面同时也会受到上游转子涡脱落尾迹的影响,使得静叶表面压力存在剧烈的非定常波动。受上下游静子尾迹及压力波传播干扰,转子通道内的激波形态也会不断发生变化。说明全环模拟能够揭示更多叶轮机械内部复杂的三维非定常流动细节。

图19 3.5级压气机压力云图Fig.19 Pressure contours of 3.5 stage compressor

6 总结与展望

本文研究开发了基于滑移网格技术、METIS网格分区技术和并行边界处理及虚拟单元技术等的多级叶轮机械全环非定常大规模并行模拟程序,以此为基础,开展了数值模拟验证和确认、并行效率测试、大规模多级非定常算例计算等工作。数值计算结果表明:

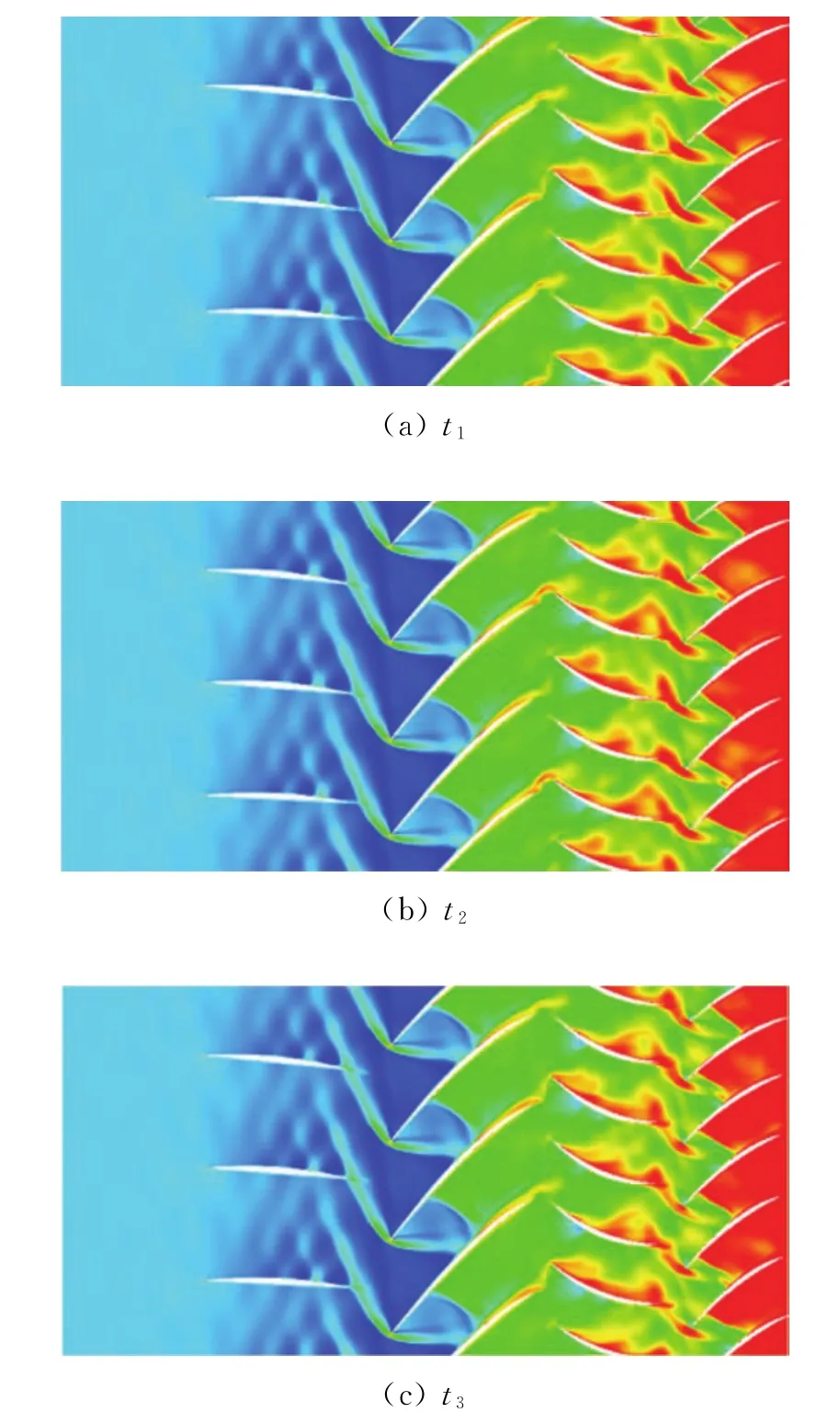
图20 前两级叶片70%叶高焓值云图Fig.20 Enthalpy contours of 70%span of first two balde row

1)全环非定常数值模拟方法得到的压气机整体气动性能与试验数据吻合良好。该方法可以消除周期性模型的限制,能够保证物理量在叶轮机械转静叶片交界面处的连续,保证交界面处物理量的连续,削弱非物理熵增,捕捉到更精细的非定常流场结构,从而为更加深入研究揭示发动机内部复杂流动机理提供技术支撑。

2)本文所采用的METIS的网格分区方法以及MPI并行策略使程序具有良好的负载均衡和并行效率,同时具备针对不同种类叶轮机械模拟的适应性。

3)对亿级规模网格的超大规模算例计算表明,本文所建立的计算方法和平台对于超大规模复杂工程应用问题具备良好的可拓展性,能够实现叶轮机械内部复杂的三维非定常流动细节模拟,可以满足实际复杂工程问题的流动分析和叶轮机械的精细流动研究要求。

综上,随着未来高性能计算技术的不断发展,本文所采用的全环数值模拟模型以及大规模并行程序策略将为揭示叶轮机械内部复杂三维非定常流动机理细节发挥更重要作用。实践证明湍流模型、插值方法等对程序模拟精度有较大影响,下一步工作中将继续针对此对程序改进提升。同时,将继续借助强大的计算平台,结合全环计算方法的优势重点进行叶轮机械非定常流动机理、压气机流动失稳等方面的研究。