基于GA-BP-AdaBoost强预测模型的大坝变形应用

王 凯,唐诗华,王江波,肖 阳,容 静，王文贯

(1.桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006;2.广西建设职业技术学院 土木工程系，南宁 530007)

0 引 言

由于大坝变形与多种影响因子密切相关,多元回归、灰色理论等传统模型不能很好地预测大坝变形趋势[1]，学者们总结出了各类模型,如支持向量机模型、神经网络模型等[2-4]。近来,人工神经网络特别是BP神经网络具有自适应、自学习和非线性拟合能力,使得BP神经网络备受青睐,如高平等[5]将其应用于大坝变形监测,取得了较好的效果。实测数据中将一定会包含随机扰动误差,传统BP神经网络模型的预测精度会有不同程度的降低。对于神经网络的缺点,Schapire创建了试图提升任意给定学习算法精度的普遍方法,即Boosting学习算法,并迅速成了新的学术热点。AdaBoost(Adaptive Boosting)算法通过迭代弱分类器而获得最终强分类器，其核心是找到最优的弱分类器[6]。遗传算法是全局化搜索的,这样就能够避开局部极小点, GA-BP遗传神经网络把遗传算法的全局优化和BP神经网络的局部寻优的特点相结合,在理论上避免了收敛慢、稳定性差和易陷入局部极小值的问题[7],如秦真珍等[8]将GA-BP算法应用于大坝边坡变形预测,取得了良好的效果;任丽芳等[9]针对深基坑变形问题,将GA-BP模型用于桥梁深基坑变形预测证明预测模型性能良好,精度高,简便易行;董春旺等[11]先建立BP-AdaBoost神经网络,然后用遗传算法寻优求解,将BP-AdaBoost-GA应用于红茶发酵性能研究并取得了很好的优化效果。

基于上述研究, 提出基于遗传算法优化BP神经网络的AdaBoost强预测模型(GA-BP-AdaBoost), 该模型把GA-BP神经网络作为最优的“弱”预测器, 用遗传算法进行全局搜索, 进而获得最优的阈值和权值, 之后再将阈值、 权值向量赋予BP网络, 利用神经网络的局部搜索能力获得网络的近似最优值。 以GA-BP遗传神经网络作为AdaBoost强预测器的“弱”预测器, 利用AdaBoost算法得到强预测器。 结合算例分析表明, 该模型在大坝变形监测中的具有一定的实用性和可行性。

1 GA-BP-AdaBoost强预测模型构建

1.1 AdaBoost强预测理论

Schapire于1990年最早提出了源自Valiant的PAC(probably approximately correct)学习模型的Boosting算法,能提高任意给定学习算法精度。1995年,Freund和Schapire将Boosting算法改进为AdaBoost算法,它们之间效率大致一样,但不用关于弱学习算法的下限,更容易处理实际问题。AdaBoost算法属于迭代算法,它是Boosting家族的代表算法,其基本思想是:最终用于决策的强分类器是由不同的弱分类器构成的,而弱分类器则是用同一训练数据集训练获得的。AdaBoost算法具体流程见文献[6，11]。

1.2 GA-BP遗传神经网络

1986年,McCelland等提出了BP神经网络,它是按照误差逆传播算法训练的多层前馈神经网络,具有良好的非线性映射能力、容错和泛化能力[12]。该模型的误差反向传播算法的基本过程[13]可以概括为:模式顺传播→误差逆传播→记忆训练→学习收敛。

1962年,Holland提出了遗传算法(genetic algorithms,GA),它是借鉴生物进化论和自然界遗传机制而成的[14]。该算法根据所选择的适应度函数计算各样本的适应度,经遗传中的交叉、变异和选择实现对优秀个体的筛选,新的群体既延续了上一代的信息,又比上一代好[11],使得种群样本不断进化,最终获得全局最优解。

GA-BP遗传神经网络在改进的BP神经网络基础上,先用遗传算法进行全局搜索,进而优化BP网络的阈值和权值,之后将阈值、权值向量赋予BP网络,利用局部搜索能力得到近似最优值。GA-BP遗传神经网络将BP神经网络的局部寻优和遗传算法的全局优化特点相结合,保证BP神经网络收敛于全局最优的同时也能够得到较为精确的优化结果,在理论上避免了BP易陷入局部极小值、网络收敛慢和稳定性差的缺点[7]。

1.3 GA-BP-Adaboost强预测模型

GA-BP-AdaBoost强预测模型使用遗传算法改进的BP神经网络为弱分类器、利用AdaBoost算法的思想将同一训练样本重复训练GA-BP遗传神经网络预测样本输出,把多个GA-BP遗传神经网络弱预测器用AdaBoost算法获取组成强预测器。GA-BP-AdaBoost强预测模型步骤如下:

① 数据预处理和网络初始化。对原始数据进行包含数据和量化归一化的预处理。从样本空间中选择m组训练数据,初始化测试数据的分布权值Dt(i)=1/m,神经网络的隐含层节点数的确定到目前仍未找到比较好的解析式来解决[15]。本文用Kolmogorov定理设定隐含层节点数为2q+1，其中q为输入层节点个数。

② 遗传算法优化BP神经网络。将BP神经网络的阈值和权值当作遗传算法的染色体,适应度函数用训练数据训练BP神经网络,把预测误差和当作个体适应度值。

③ 寻找弱预测器gt(t=1,2,…,T)。对第t个弱预测器进行训练时, 将GA-BP遗传神经网络用训练数据训练并且预测训练数据输出,得到关于预测序列g(t)的误差和et：

(1)

g(t)=≠y。

其中：y为期望分类结果;g(t)为预测分类结果。

④ 计算预测序列权重。 根据预测序列g(t)的预测误差和et, 推算序列的权重at。

(2)

⑤ 更新权重。 下一轮训练样本的权重根据预测序列权重at进行调整

i=1,2,…,m。

(3)

式中:Bt是归一化因子, 这是为了使分布权值的和为1。 其中

(4)

⑥ 强分类器函数。训练T轮之后获得T个弱预测函数gt(x)(t=1,2,…,T), 然后由T个弱预测函数加权组合, 就可以得到一个强预测函数H(x):

(5)

2 算例分析

为了验证模型的有效性及精度,以某蓄能水电厂的下库大坝变形监测为例,对位于下库大坝的河床坝段坝顶的2号观测点在2000-04-12—2004-06-25这段时间的坝体温度、水位、时间和大坝Y向变形量进行了63次非等时间间隔观测,为了方便建立模型,用Hermite插值法把63期非等时间间隔数据调为64期等时间间隔变形数据[3],其变形值如图1所示。可见,大坝的变形受到多种因素影响,具有较强的随机性变化,并且呈非线性变化趋势。

图1 大坝变形实测值Fig.1 Measured deformation value of dam

拟通过3种方案进行分析:方案1—标准BP神经网络预测模型，方案2—遗传BP神经网络预测模型(GA-BP)和方案3—遗传算法优化的BP-AdaBoost强预测模型(GA-BP-AdaBoost)。各方案采用了前50期变形观测数据当作样本训练,后14期当作测试样本。为了方便比较,各方案均采用BP神经网络标准模型,隐含层和输入层之间采用Sigmoid函数。各方案BP网络结构参数具体为:输入层节点数均为3、输出层节点数均为1、隐含层节点数均为7,动量项系数和学习率均为0.01,最大循环次数均设置为20。遗传算法种群范围设定为10,选择操作选用轮盘赌法,变异概率和交叉概率分别为0.1和0.3,最大迭代次数均为30。方案1的初始权值和网的连接权值由模型中的代码随机生成,而方案2和3,利用遗传算法优化BP神经网络。通过对这3个方案模型在大坝变形数据中的预测精度分析,探讨各种模型的预测性能,并验证GA-BP-AdaBoost强预测模型的可行性与优越性。采用平均绝对值、均方根误差和平均百分比误差来评定各模型预测精度:

1) 平均绝对误差(MAE)

(6)

2) 均方根误差(RMSE)

(7)

3) 平均绝对百分比误差(MAPE)

(8)

用大坝监测原始数据输入各模型来训练, 获得预测输出值。 各方案模型的计算结果对比见表1。

表1 各模型计算结果

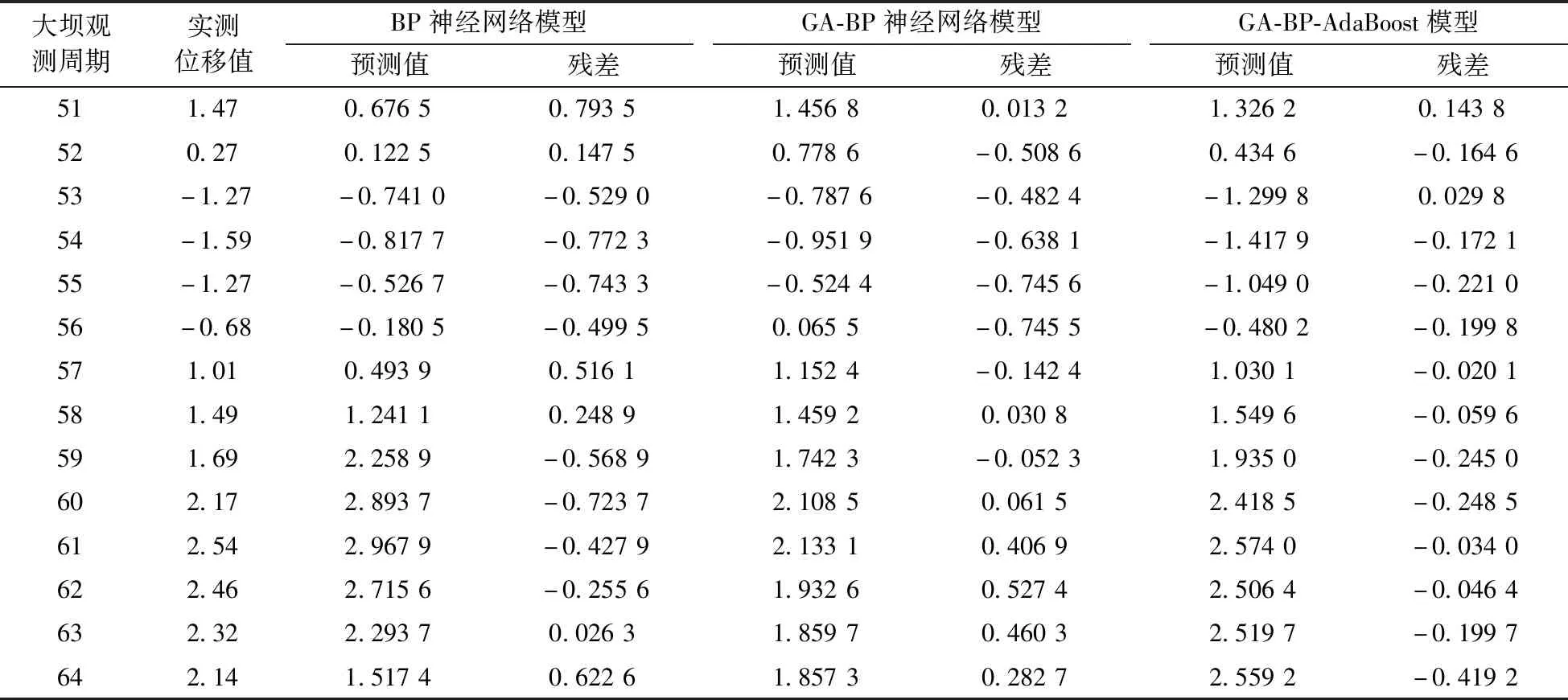
Table 1 Contrast of each model calculation results mm

可见,方案1的标准BP神经网络预测模型的残差很大,模型残差序列绝对值超过0.6 mm的有5期,最大残差达到0.793 5 mm,方案2 GA-BP神经网络模型的预测残差序列绝对值超过0.6 mm的有3期,最大残差达到-0.745 6 mm,说明遗传算法优化的BP神经网络模型在大坝变形预测精度上较标准BP神经网络有了很大幅度的改进,遗传算法最终训练结束时还是由期望输出目标决定的,虽然算法运行速度得到了提升,但是预测精度并没有显著提高。方案3 GA-BP-AdaBoost强预测模型的预测残差序列除最大残差外,其余各期均低于0.3 mm,而最大残差为-0.419 2 mm。表明该模型在大坝变形预测精度上较方案1和2有了大幅提升。

从各模型变形预测值和实际变形值对比(图2)可知,方案1和方案2在大坝变形预测段的前期和中期,两者的变形趋势基本一致且预测值相差不大,在后期两者出现背离。方案3GA-BP-AdaBoost模型预测值在整体变化趋势上与大坝实际变形值相一致,且两者之间的差值相比方案1和方案2很小,表明方案3可以很好地预测大坝变形趋势。

图2 各模型预测值和实际值对比Fig.2 Comparison of predicted and actual values of each model

由残差图(图3)可知,方案1的残差波动范围最大,方案2较方案1波动范围有所减小,而方案3的残差波动范围几乎稳定在0.2 mm以内。表明GA-BP-AdaBoost强预测模型具有很高的全局预测精度,且预测性能较为稳定。

为进一步综合评定各种模型的性能,采用均方根误差、平均绝对误差和平均绝对百分比误差3项指标进行评定,各预测模型的精度指标计算见表2。

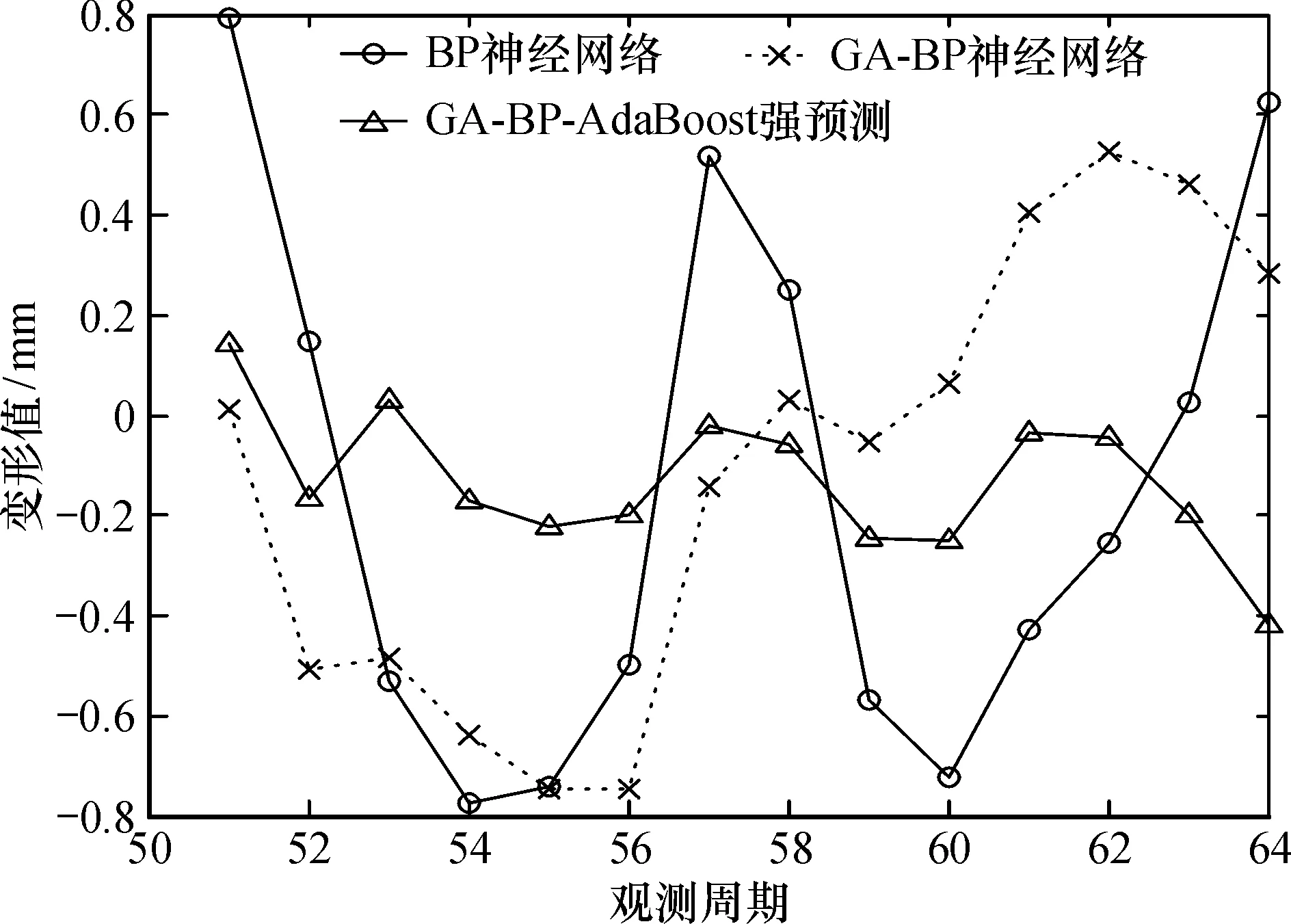
图3 各模型残差对比Fig.3 Residual comparison of models

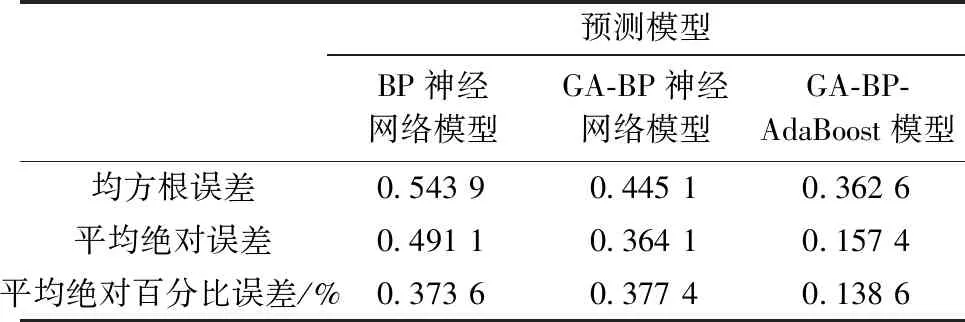
Table 2 Contrast of precision of each model mm

对各模型的预测精度而言, 方案1较方案2在均方根误差和平均绝对误差指标方面, 精度略低, 分别为0.543 9和0.491 1 mm, 但是两者在平均绝对百分比误差方面精度几乎一样, 反而标准BP神经网络稍高于GA-BP遗传神经网络模型, 说明遗传算法对于BP神经网络预测模型的精度提高有限。方案3 GA-BP-AdaBoost强预测模型各项精度指标在3种模型中均是最小的,分别为0.362 6 mm、0.157 4 mm、0.138 6%,这表明,AdaBoost强预测器根据预测误差调整若干组弱预测器之间的权重,能够把遗传算法随机选择交叉、变异优化后的BP神经网络不同的预测结果综合起来,实现AdaBoost强预测器“优中选优”的目标,最大限度地提高了模型预测精度的同时也验证了提出的基于遗传算法优化的BP-AdaBoost强预测模型在大坝变形监测中的优越性和可行性。

3 结束语

经理论和算例分析,并与标准BP神经网络模型、GA-BP遗传神经网络模型对比表明,标准BP神经网络模型由于要设定适宜的模型参数,并且初始阈值和权值是系统任意给定的,具有不确定性的预测结果;GA-BP遗传神经网络模型虽用遗传算法经由随机选择变异、交叉优化了BP神经网络的权值和阈值,弥补了BP神经网络容易陷入误差函数的局部极值点的缺陷,在预测精度上有了一定程度的提高,最终阈值和权值仍由期望输出目标决定的,预测精度和稳定性仍待提高;而GA-BP-AdaBoost强预测模型的弱预测器同时融合了遗传算法全局优化和BP神经网络的局部寻优特点,同时AdaBoost强预测器能够通过给弱预测器的若干预测序列赋予不同的权重,综合了不同预测序列的优势,实现了AdaBoost强预测器“优中选优”的目标,最大限度的提升了预测精度,证实了提出的基于GA-BP-AdaBoost强预测模型在大坝变形监测中的可行性和实用性。通常GA-BP-AdaBoost强预测模型更加适合非线性模型,但针对一些因为样本数量小、样本分布不均匀而造成神经网络预测误差大的问题,还有待后续进一步研究。