快锻液压机液压管路流固耦合分析
2019-08-28赵信智白双宝
赵信智 ,白双宝
(1.兰州兰石能源装备工程研究院有限公司,甘肃 兰州 730050;2.甘肃省大型快锻液压设备工程研究中心,甘肃 兰州 730050;3.甘肃省金属塑形成型装备智能控制重点实验室,甘肃 兰州 730050)
快速锻造液压机液压系统为快锻液压机工作提供动力源,主要包括以下几个部分:循环系统、主泵系统、高压系统、充液卸载系统、控制系统、辅助系统。
快锻压机的液压系统采用定量柱塞泵或者变量柱塞泵作为供液泵。由柱塞泵供液会产生的压力脉动,供液泵形成的压力脉动油液会造成液压管路系统振动冲击,严重时使管路系统遭到破坏,影响设备的正常运行[1]。快锻压机供液泵脉动式的输出油液使管道产生强迫振动和谐振,如果管道固有频率与供液泵脉动频率和流体谐振频率接近,则会产生流固耦合振动[2]。液压管路的流固耦合振动会严重危害快锻压机设备的平稳性和可靠性,甚至导致严重事故的发生[3-4]。因此,了解快锻压机液压系统管道流固耦合振动的机理,对于设计运行平稳的快锻压机设备以及对现有设备的液压系统振动抑制都是非常重要的。
1 液压管道的建模
1.1 管道流固耦合数学模型
目前,流固耦合计算的数学模型是从流体力学N-S方程和固体力学小变形弹性理论导出的求解FSI的基本方程,并将这些基本方程简化得到。在计算流体域和结构耦合作用的数学模型时,通常分别讨论流体域和管道结构,最后通过流体和管道的耦合边界条件进行合成[5-6]。
(1)流体运动描述
表述流体运动的最基本的原理是运动连续方程、动量方程和能量方程。在柱坐标系下(z-轴向、r-径向、θ-周向),可压缩流体的连续性方程为:

式中:ρf为可压缩变化的流体密度;fr为横向体积力密度;fz为轴向体积力密度;t为时间;vr、vz分别为横向和轴向速度;μ 为液体的体积粘度;ρf、vr、vz和p 均分别为 z、r、t的函数。
(2)管道运动描述
在不考虑弯曲、剪切变形及截面旋转变形对管道运动的影响时,管道的运动方程为:
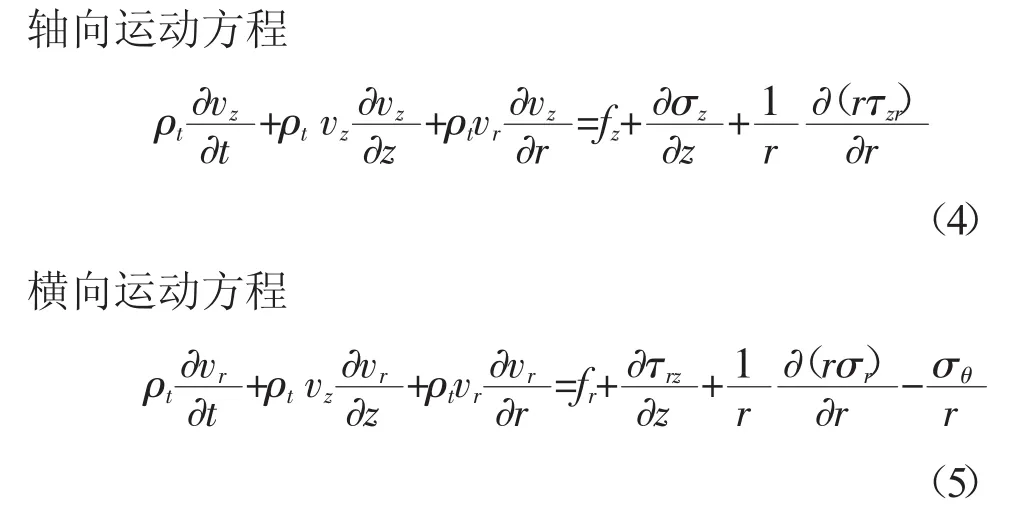
式中:vz、vr为管道轴向和横向速度;ρt为管壁材料的质量密度 σr、σz、σθ分别柱坐标中各个方向的平均应力;τzr、τrz为剪应力。
(3)流固耦合边界条件
考虑管道和流体耦合的4-方程模型。

式中:Vf为流体平均速度;P为流体平均压力;ρt为流体平均密度;Kf为流体体积模量;vz、σz分别为管道轴向平均速度、平均应力;R为管道内半径;E、v分别为管道弹性模量和泊松比;τw为管道与流体间的摩擦力[7-9]。
1.2 液压管道流固耦合振动基本规律
在快锻压机液压系统中柱塞泵的脉动式流量输出是造成流体管路中压力脉动的根源,压力脉动与管路中流体的谐振是不可避免的,当柱塞泵的脉动频率接近流体管路的谐振频率时压力脉动将得到加强[10-11]。在这种情况下,如图1所示,液压管道流固耦合振动有以下基本规律:

图1 管道流固耦合振动基本规律
(1)流体的压力脉动频率接近管道的固有频率。这时管道将会以最大幅值的振动,导致管道、管夹损坏等。
(2)如果液压管路没有发生流固耦合振动,但是管道内壁上的压力脉动超过管道材料的许用应力极限,也会导致管道、管夹破损等。
(3)压力脉动即使幅值比较小,仍能够产生作用于管夹上的激励力,这个激励力会使管夹内表面发生微动磨损,随着磨损的加剧,最终使管夹遭到破坏。失去支撑的管道,固有频率会极度降低,当管道固有频率与压力脉动频率接近时发生流固耦合的振动,造成管路系统破坏。
2 液压管道流固耦合仿真设计
2.1 设计1——不同支撑间距直管有限元仿真
对直管道管夹布置,分别布置0个管夹、布置1个管夹、布置4个管夹、布置9个管夹情况下对直管道进行仿真[12-14]。Workbench有限元仿真过程包含3个步骤:前处理、求解和后处理。
在有限元软件workbench中建立管道模型,直管有限元模型如图2所示。取快锻压机管路系统中的一段直圆管为模型,管道长度L=10000mm,管道内径d=139mm,壁厚t=40mm;管道材料物性参数,密度ρ=7800Kg/m3,弹性模量 E=210GPa,泊松比 v=0.3,忽略管道阻尼,所用单元为SOLID186。

图2 直管有限元模型
边界条件:对管道两端采取固定约束条件,管道中管夹布置处采用固定约束条件,并对直管在不同支撑结构间距下进行模态分析[15]。管道结构网格划分采用ANSYS-workbench里的meshing进行划分[16-17]。管道管夹布置有限元模型如图3所示。

图3 管道管夹布置
计算结果及分析:仿真得到直管道在不同支撑间距下的1~5阶的固有频率,计算结果如表1所示。
从表1可以看出,随着在长度为10000 mm管道上布置管夹个数的增加,管道的1阶、2阶、3阶、4阶和5阶固有频率都呈增加的趋势;其中对管道不布置管夹时管道的1~5阶固有频率都最小,而随着布置管夹个数增加到9个,管道1~5阶固有频率远大于不布置管夹的时候。不同管道支撑结构管夹间距布置对管道固有频率有明显的影响,从1个管夹增加到9个管夹,管道的1阶固有频率增幅达到20倍左右,并随着阶次的增加,增幅减小。
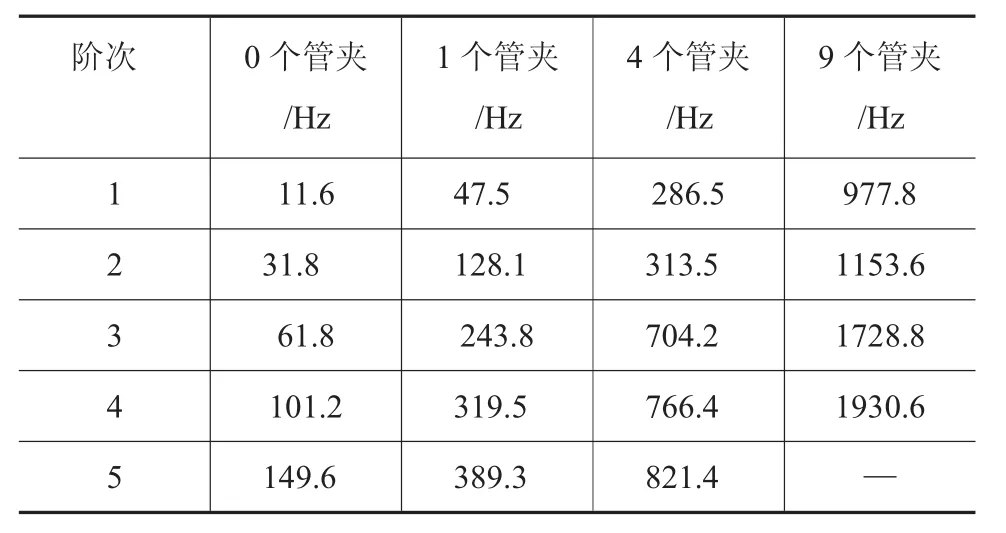
表1 不同管道支撑间距对管道固有频率的影响
2.2 设计2——不同管道壁厚流固耦合有限元仿真
快锻压机液压管路系统中管道壁厚对系统的承压、系统的振动及系统的安全可靠都有较大的影响,下面的仿真将考虑流固耦合对不同管道壁厚圆管的影响[18-19]。
前处理在Workbench中建立有限元模型,管道长度L=2000mm,管道内径d=139mm,壁厚t1=5mm,t2=10mm,t3=20mm,t4=30mm,t5=40mm;管道材料为碳钢,密度 ρ=7800Kg/m3,弹性模量 E=210GPa,泊松比v=0.3,忽略管道阻尼,其所用单元为SOLID186;流体为液压油,密度ρ=860Kg/m3。管道结构和流体域的网格划分均采用Workbench中的meshing进行划分。
流固耦合边界条件:入口设置速度边界条件10 m/s,出口设置自由边界条件,流固耦合流程如图4所示,流体域有限元模型如图5所示。

图4 管道流固耦合流程图

图5 流体域有限元模型
计算结果及分析:计算直管道在不同壁厚条件下,管道在沿X、Y和Z轴方向的应力和位移分布,分析在流固耦合作用下管道壁厚对管道变形的影响,计算结果如表2所示。
从表2中可以看出,随着壁厚的增加,管道的最大变形呈减小趋势,其中管道壁厚在5mm时的变形量约为管道壁厚在40mm时的10倍。
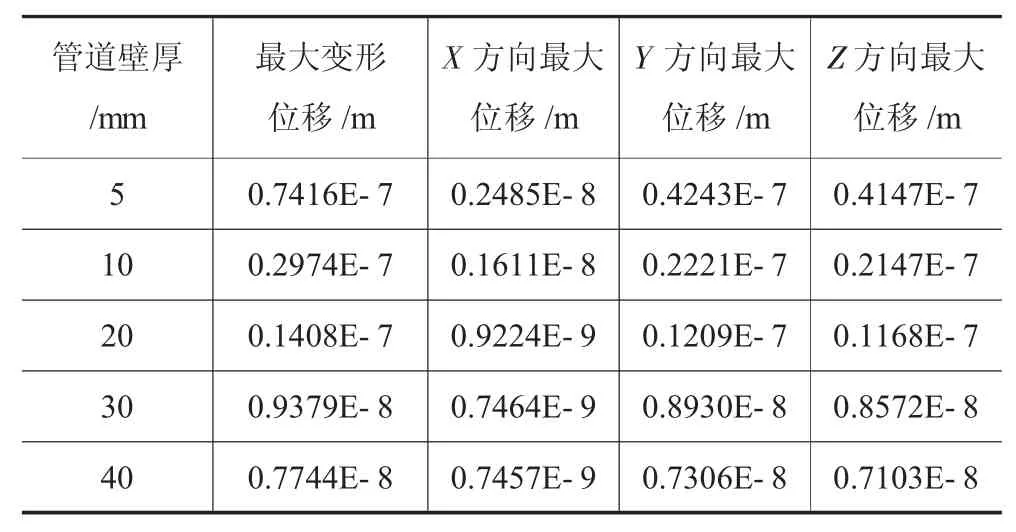
表2 不同管道壁厚流固耦合作用下位移比较
2.3 设计3--不同流体流速下直管道流固耦合有限元仿真
快锻压机液压系统在设计之初,要考虑管道流速,以匹配适合的系统压力和负载速度,因此设计人员需考虑在不同流速下管道流固耦合对管道结构的影响。
在Workbench中建立有限元模型,管道长度L=1500mm,管道内径d=36mm,壁厚t=12mm,管道材料为碳钢,密度ρ=7800Kg/m3,弹性模量E=210GPa,泊松比v=0.3,忽略管道阻尼,其所用单元为SOLID186;流体为液压油,密度ρ=860Kg/m3。管道结构和流体域的网格划分均采用ANSYS-workbench里的meshing进行划分。入口边界条件V1=1m/s、V2=3m/s、V3=5m/s、V4=7m/s、V5=10m/s,出口设置为自由边界条件。进行单向流固耦合,将不同流速下计算得到的流体对管壁的压力作为管道的边界条件进行求解,流固耦合面如图6所示。

图6 流固耦合面
计算结果与分析。分别计算不同流速下管道在沿X、Y和Z轴方向的应力和位移分布,分析在流固耦合作用下不同流速对管道变形的影响,计算结果如表3所示,图7和图8分别为不同速度下的计算结果云图。
从计算结果可以看出:(1)在对直圆管两端固支约束的条件下,直管在流固耦合作用下主要表现为管道结构的位移;其中管道轴向X方向有较大的摆动,在管道截面Y、Z平面内管道表现为弯曲、扩张及收缩;(2)从管道位移云图可以看出,在流固耦合作用下,管道的最大应力在液压有入口部分内侧;(3)从表2.3可以看出,随着管道流速的增加,管道结构的总位移、X方向位移、Y方向位移、Z方向位移及管道结构的最大应力都呈增大趋势,并且随着流体流速的增加,这种趋势越来越明显。

图7 流速为1m/s时仿真结果

表3 不同管道流速流固耦合作用下位移应力比较

图8 流速为10 m/s时仿真结果
3 结论
随快锻压机向着高压大流量方向发展,对于管道流固耦合振动的问题不得不引起足够的重视。本文总结了快锻压机液压管路流固耦合振动的规律,并在此基础上利用液压管路流固耦合数学模型,采用有限元仿真软件ANSYS-workbench,详细分析了不同管道支撑结构间距、不同管道壁厚、不同管道流体流速的流固耦合振动情况。
(1)不同的管夹间距对管道的固有频率影响较大,设计人员在设计时应合理的布置管道管夹,应避免管道系统的固有频率与流体的谐振或者脉动频率接近。
(2)固体管道壁厚和流体流速对管道安全也有较大的影响,液压泵脉动压力过大,使得管道内流体流速增大,管道振幅和振动频率增大,从而影响系统安全。
