镍铝青铜高温热压缩流变行为研究
2019-08-28马艳霞周铁柱
苑 伟,罗 皓,马艳霞,周铁柱,郁 炎
(中国船舶重工集团公司第七二五研究所,河南 洛阳 471023)
镍铝青铜是以镍、铁、锰为主要添加元素的一种复杂多相的铜合金,具有较高的强度、韧性以及优异的耐腐蚀性能,广泛应用于船舶螺旋桨、阀门、轴套等产品[1,2]。该类合金产品多为铸件,存在着成分偏析、晶粒粗大、气孔夹渣等缺点,对其性能及使用寿命有较大影响,限制了合金的应用[3]。因此,对变形态镍铝青铜展开研究是具有深远意义和现实价值的。本文通过高温热压缩实验对镍铝青铜合金流变应力进行研究,分析其高温变形时的流变应力行为并建立本构方程,为制定合理的热加工工艺和有限元模拟提供理论依据[4]。
1 实验方案
实验采用的是半连续铸造方法制备的镍铝青铜合金铸锭,其化学成分为我公司设计,主要元素包括Ni、Al、Fe、Mn 以及少量的 Cr。热压缩实验在 Gleeble-3500热模拟实验机上进行[5]。热压缩实验前,铸锭经均匀化处理。压缩式样尺寸为ø10mm×15mm。实验过程中,试样两端需涂抹润滑剂并粘贴石墨片,以减少试样与机器压头之间的摩擦,确保试样在热压缩过程保持均匀变形。变形温度分别是750℃、800℃、850℃、900℃、950℃,应变速率分别是0.01s-1、0.1s-1、1s-1、10s-1,变形量为 60%。将试样以10℃/s的升温速度升至试验温度后保温5min,热压缩实验完成后立即对试样采用水淬处理以保留其高温变形后的组织。
2 结果与讨论
2.1 合金的热变形的真应力-真应变曲线
图1是镍铝青铜合金在热压缩变形时不同应变速率下的真应力-真应变曲线。从图1可以看出,流变应力主要与变形温度和应变速率以及变形程度有关,主要具有以下特征:①在初始应变期(ε<0.03),流变应力呈线性快速增长并在ε<0.2时会达到峰值,之后保持缓慢变化,表现出稳态流变特征;②在相同的变形温度下,流变应力随着应变速率增大;在相同变形速率条件下,流变应力随着变形温度的升高而降低。
在塑性变形初始阶段,位错迅速增殖,位错密度越大材料变形抗力越大,这一阶段主要以加工硬化为主。随着应变的增加,位错会产生滑移和攀移使材料软化,加工硬化与软化相互抵消,流变应力不再随应变发生大幅变化逐渐达到动态平衡的状态,这一阶段以动态回复或再结晶为主。温度越高,热激活作用越强,原子间作用力下降,位错运动的派纳力减小,材料有足够的能量进行滑移和攀移,同时临界剪应力降低,可以开动的滑移系增加,从而使得变形抗力有所下降。在一定的温度下,应变速率越快,材料塑性变形时无充分时间进行位错的湮灭、抵消运动,变形抗力增加。

图1 不同应变速率下镍铝青铜合金热压缩变形的真应力-真应变曲线
2.2 本构模型的建立
材料在热变形过程中均存在热激活过程,这一状态下的流变应力取决变形温度T和应变速率,并存在一个加工硬化与动态软化逐渐达到动态平衡的过程。为此,可采用Arrhenius方程来描述材料在热变形过程中流变应力和变形温度与应变速率之间的关系[6]:

通过简化,低应力和高应力状态下的流变应力和应变速率之间的关系可以分别用幂指数函数与指数函数进行描述[7]:
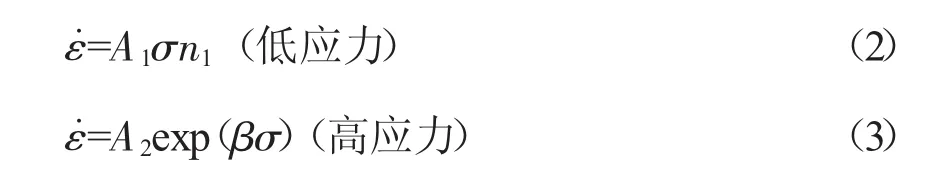
式中:σ 为流变应力;n1、n、β、A、A1和 A2为与材料有关的常数,α=β/n1;R 为摩尔气体常数,8.314J/(mol·K);T为热力学温度,K;Q为材料形变激活能,J/mol。
根据Zener和Hollomon的研究,材料在高温塑性变形时应变速率与温度T对材料变形的影响可以用Zener-Hollomon参数(Z参数)表示[8]:
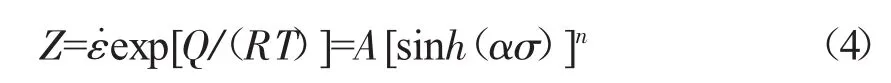
对式(2)和式(3)两边分别取对数得到:

假设Q与温度T无关,R、α、n和A均为常数,对公式(1)两边取对数,可得式(7),即
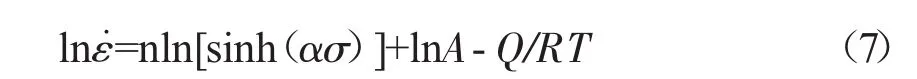
对公式(7)求偏微分即可得到Q的计算式,即

只需求得 A、n、α、Q 等值并带入式(1)中,即可获得合金的热变形本构方程。
本文中,流变应力采用峰值应力进行分析,如表1所示。
根据式(2)和式(3),绘制不同温度条件下,镍铝青铜合金的“ln()-σ”和“ln()-σ”的关系曲线,并利用最小二乘法分别进行线性回归,如图2和图3所示。β值可以由图2中高应力状态下的三条拟合直线斜率的平均值计算得到,可得β=0.0598;n1可由图3中低应力状态下的三条拟合直线斜率的平均值得到,n1=4.54。则,α=β/n1=0.0132。

表1 合金在750-950℃区间不同热变形条件下的峰值应力(σp/MPa)
根据式(8)可求得形变激活能Q=209.108kg/mol。将Q值带入式(4)可得对应的Z值,对式(4)取对数得:

图2 ln-σ 之间的关系

图3 ln-lnσ 关系图

图4 ln-ln[sinh(ασ)]之间的关系图

图5 ln[sinh(ασ)]-1/T 之间的关系图
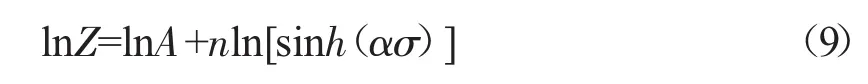
lnZ和ln[sinh(ασ)]的关系如图6所示。lnA为拟合直线的结局。根据拟合数据可知,lnA=29.302,A=5.349×1012,线性拟合系数为0.9943。

图6 实验合金的lnZ-ln[sinh(ασ)]关系图
将求得的材料参数带入式(1)即可得到试验范围内所有应力状态的流变应力本构方程:

将在实验条件下获得的镍铝青铜合金峰值应力与利用本构方程的计算值进行对比,如图7所示。根据误差分析显示,通过本次试验所建立本构方程得到的不同条件下峰值应力计算值与实测值的相比,仅在(T=850℃,=1s-1)处误差超过 10%,说明表明本构方程能较好地描述合金的高温流变行为。
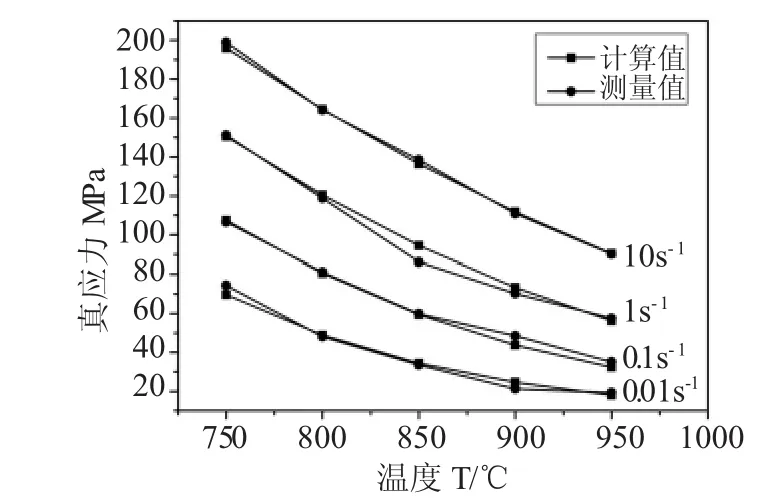
图7 不同热变形条件下实测峰值应力与计算峰值应力比较
3 结论
(1)镍铝青铜合金的流变应力受变形温度和变形速率的影响。在变形温度为750℃~950℃,应变速率为0.01~10s-1范围内,流变应力随着应变温度的升高而降低,随着应变速率的增加而增大。
(2)镍铝青铜合金的热变形行为受热激活过程控制,其变形激活能Q=290.108KJ/mol。该合金的热变形本构方程为:

