风险价值分析——以皖通高速为例

● 刘玲玲

一、样本的建立与数据的基础性分析

本文选取了皖通高速2017年12月21日至2018年12月28日每日股票收盘价，共250个数据构建样本。

（一）皖通高速的总体趋势

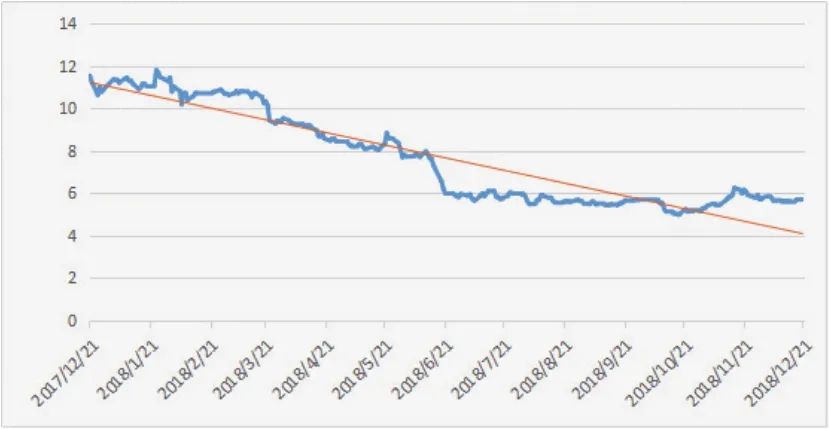
图1.1 皖通高速股价趋势图

从折线图中可以看出，样本期间皖通高速的股价最高上涨至11.8元，最低下跌至4.98元，在这一区间内呈震荡起伏的特征，总体趋势下滑，这一点从趋势线中看得更明显。2018年5月以来，股价呈明显下跌态势。

（二）描述性统计指标的分析

可知皖通高速股价在样本期间最高为11.8元，最低为4.98元，均值为7.6元，中位数为6.11元，众数为5.98，从数值上来看，均值不处于中位数和众数之间，这说明样本数据是一个对称分布［1］。进一步看偏度和峰度指标。峰度K=-1.36＜0，偏度S=0.5＞0，这表明样本数据不服从正态分布。

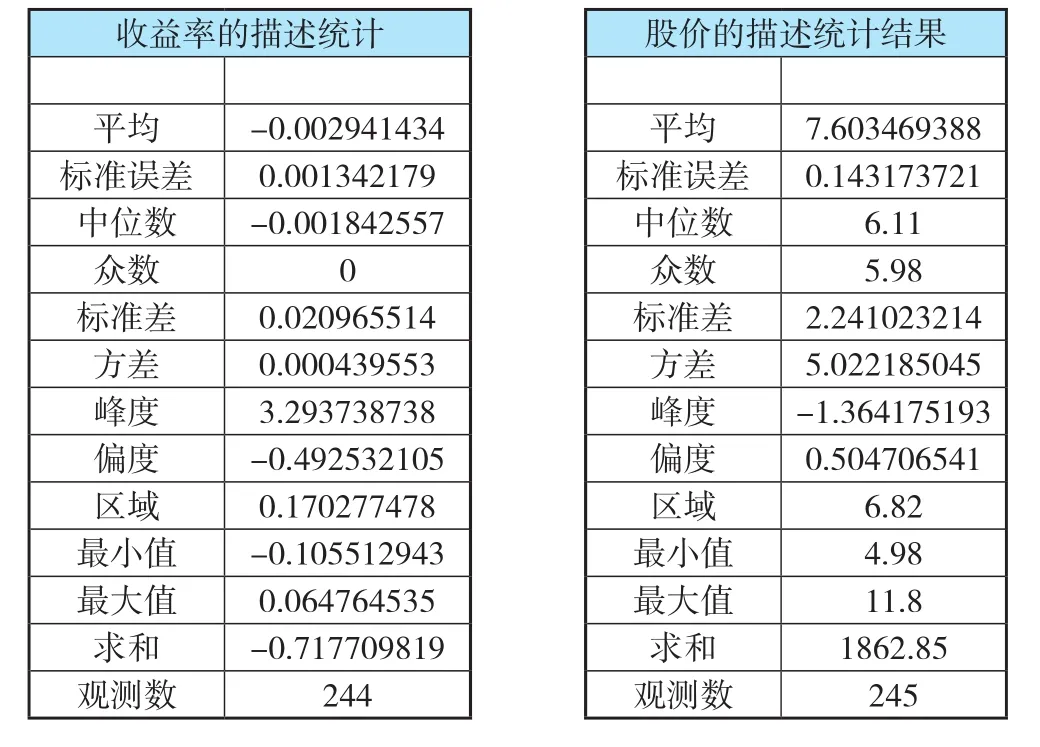
表1.1 皖通高速收益率及股价描述统计

（三）绘制直方图

前面已知皖通高速股价介于4.98-11.8元之间，假设按0.30元为一个划分频距，生成一系列间隔为“0.60”的数据，最大值为“12.1”的直方图。同理可得皖通高速的收益率直方图。如图1.3所示。

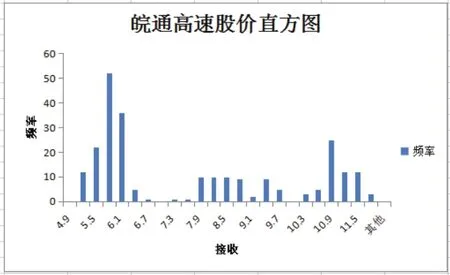
图1.2 皖通高速股价直方图

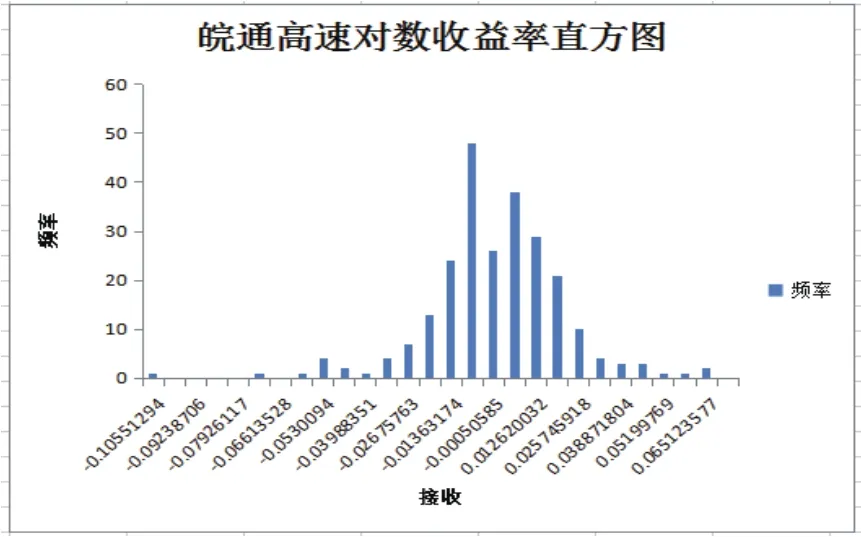
图1.3 皖通高速对数收益率直方图

通过股价和收益率直方图可以发现，皖通高速的波动性具有金融资产波动的通性及尖峰后尾分布，集聚性和非对称性等。

（四）绘制正态分布图

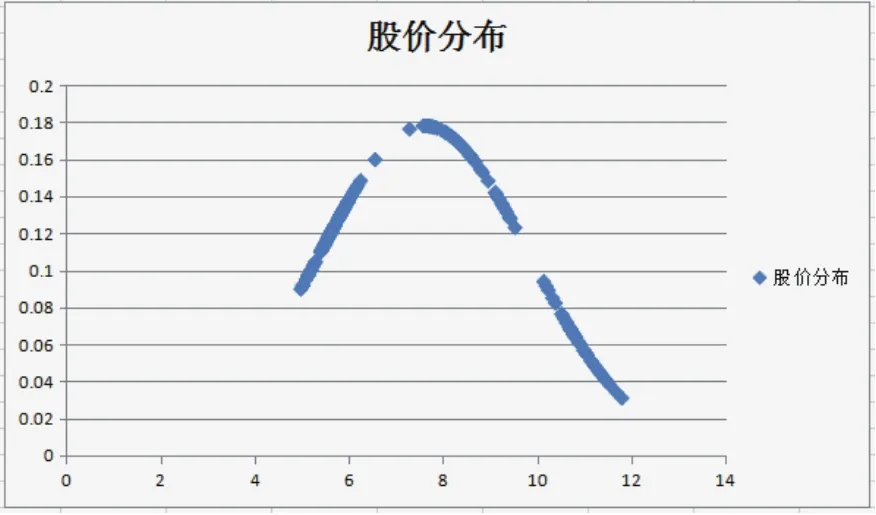
图1.4 皖通高速股价分布图

下图为皖江高速股票对数收益率的正态分布图，可以看出其呈明显的尖峰厚尾且左偏的分布特征。

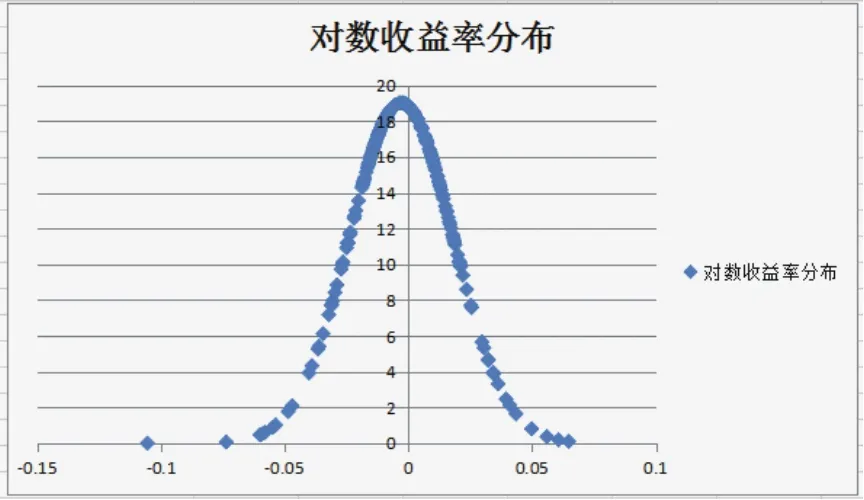
图1.5 皖通高速对数收益率分布图

这些现象都表明股价处于均值附近、高收益区域和高亏损区域出现的概率大于正态分布决定的概率，同时，我们不能用理论的正态分布来刻画收益率，这样会低估极端事件的发生。

在了解了股票收益率特征的基础上，可以假设用VaR法来估算一项投资的风险价值。根据估算模型和波动性模型的不同，可以将VAR的计算方法分为三类：分别为历史模拟法、蒙特卡洛模拟法和方差—协方差法。此处分别用三种方法计算：假设我们已知在2018年12月21日某投资者买了10000股皖通高速股票，购入价格为5.63元/股。接下来的问题是，下一个交易日，在99%置信水平下，该投资者的最大损失是多少？

二、用模拟法获取VaR

（一）用历史模拟法获取VaR

在历史模拟法下，对该问题的解决步骤如下：

1.确定风险因子。本例中我们只考虑皖通高速股票本身的变动，不引入其他因子（如股票指数变动、利率变动等），即通过资产价格计算资产损益。具体地说，皖通高速的损益R是股价P的函数，用公式表示：股票损益Rt=卖出价Pt-买入价Pt-1。

2.建立样本。根据巴塞尔委员会和我国银监会的要求，历史模拟法的样本数据至少应包括250个。另外考虑到样本数据的时效性和可参照性，本例选择2017年12月21日至2018年12月21日每个交易日的皖通高速收盘价，共245个数据建立分析样本。

3.模拟头寸损益。将10000股皖通高速头寸回放到过去的255天中，可获取本投资其在每一个历史交易日中的价值，然后模拟头寸价值序列值Vt=Pt*10000，进而计算模拟头寸的逐日损益Rt=Vt-Vt-1。如图所示为模拟的部分数据：

4.求解VaR。获取VaR数值有两种方法，此处是通过excel来求解。主要是将损益序列中的数据按升序排列，找到对应的第254×1%=2.54个数据，大约位于-7200到-6600元之间。如图所示，为谨慎起见，可选择VaR=7200元 。

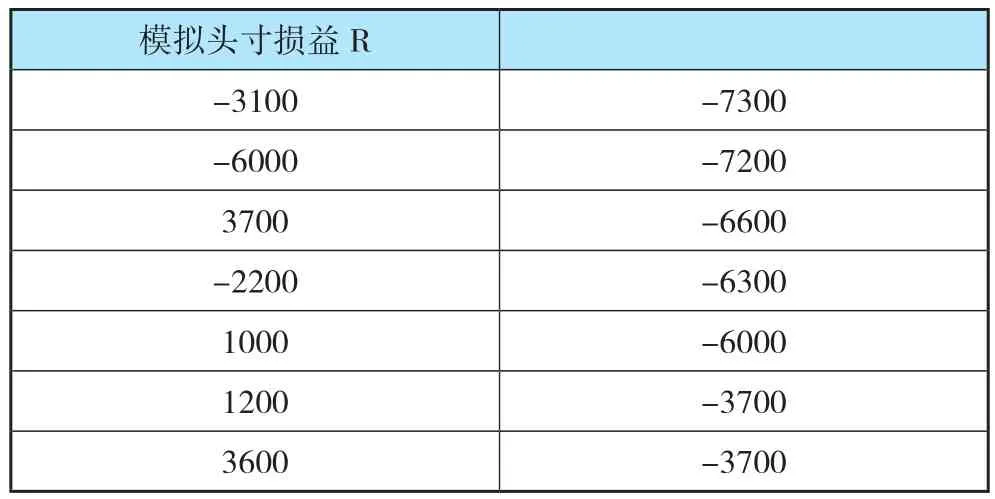
表2.2 损益数据升序排列值

（二）用基于随机游走模型的蒙特卡罗模拟法获取VaR

在基于随机游走模型的蒙特卡罗模拟法下，对该问题的解决步骤如下：

1.确定风险因子。本例中我们只考虑皖通高速股票本身的变动，不引入其他因子（如股票指数变动、利率变动等），即通过资产价格计算资产损益［2］。具体地说，皖通高速的损益R是股价P的函数，用公式表示：股票损益Rt=卖出价Pt-买入价Pt-1。

2.选择随机模型并检验。假定皖通高速股票价格变动服从随机游走模型，Pt=Pt-1+εt。

接下来我们需要对这一假定进行检验。我们这里选取的随机游走模型实际上是一个非稳定的一阶自回归模型。因此，模型的检验主要从两个方面入手：（1）股价序列是不是具有平稳性？（2）股价序列是不是具有自相关性和偏自相关性？选择2017年12月21日至2018年12月21日每个交易日的皖通高速收盘价，共245个数据建立分析样本。

首先检验股价序列的平稳性。单位根检验是检验时间序列是否平稳的最常用方法，在EVIEWS中对皖通高速股价序列做单位根检验，以观察其是否具有平稳性［3］。得结果如下：

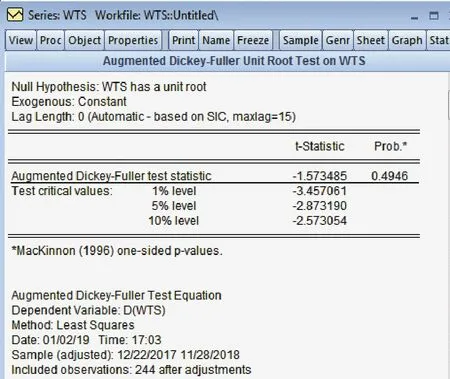
图2.1 皖通高速股价平稳性检验

ADF检验t统计量为-1.573485，大于显著性水平为10%的临界值，表明皖通高速股价序列是非平稳的，即序列WTS有单位根，接受原假设的概率为49.46%。接下来做自相关性检验。得结果如下：

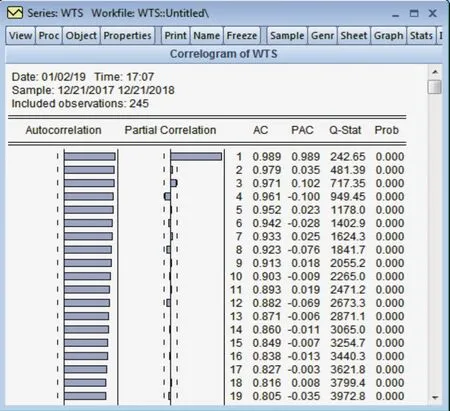
图2.2 股价自相关性检验

由上图可看出，序列WTS存在着明显的自相关性，同时具有滞后一期的偏自相关性。

综合以上检验结果，我们可以得出结论，皖通高速股价序列服从随机游走模型。即可以用随机游走模型来模拟皖通高速股票价格的未来变化。

3.模拟股票价格序列，并计算头寸损益。已知皖通高速的基期价格P0=5.63，下一期的价格就是在基期价格的基础上加上一个随机变量。假设我们做一万次模拟，那么就需要产生一万个虚拟变量，考虑到涨跌停板限制，给定变量取值范围为（-5.63，5.63）。采用函数法，将P0=5.63和产生的随机数代入公式Pt=P0+εt，进行模拟操作，得到模拟价格序列。

再利用公式Vt=Pt*10000，获得模拟头寸价值的时间序列，进而计算模拟头寸的逐日损益，即：Rt=Vt-V0，获得模拟头寸损益的时间序列。详见下表：

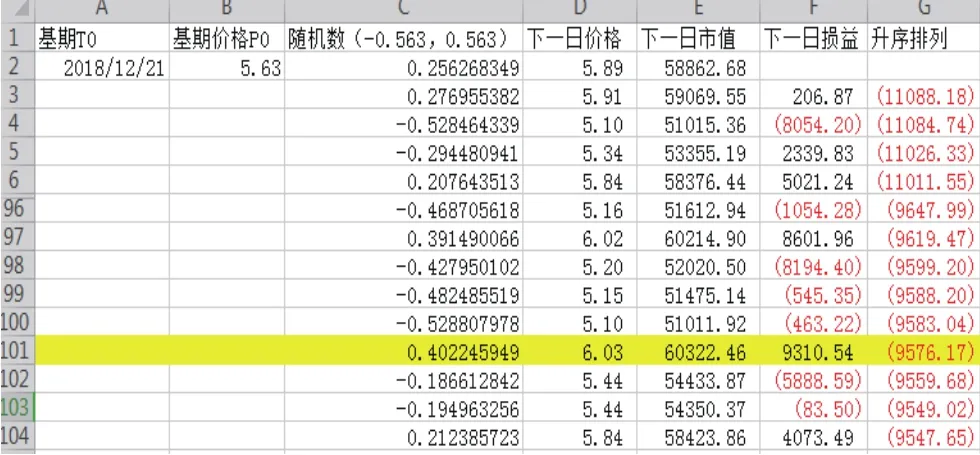
图2.3 模拟头寸损益的时间序列

4.求解VaR。与历史模拟法相同，可以用两种方法获取VaR值。

方法一：将模拟损益序列中的数据按升序排列，找到对应的第9999×1%≈100个的数据，可得VaR=9583元

方法二：直接用EXCEL中的“排位与百分比排位”函数，找到对应1%的损失值，可得VaR=9576元

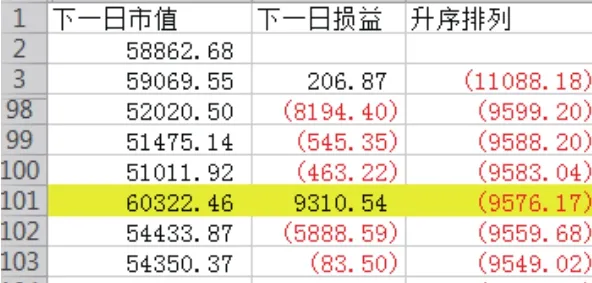
图2.4 损益序列

（三）综合比较分析

历史模拟法计算出来的VaR=7200元，而基于随机游走模型的蒙特卡罗法计算出来的VaR=9583元，二者存在着较大的差异。其原因在于这两种方法的基本设计原理不同［4］。

历史模拟法为向前模拟，以历史真实交易数据为样本，与样本期内变量的波动幅度有关。在整个样本期内，“坏的情景”出现的次数及其程度对最终的结果有着关键性的影响。

而基于随机游走模型的蒙特卡罗法为向后模拟，以当前情景为起点，模拟变量的未来变化，因此，当前情景的好坏对最终结果的影响非常大。

此外，样本量的不同也是导致二者存在差异的原因。在历史模拟法下，样本数据来自于真实的历史交易，一般样本长度为1-3年，即250-750个交易日。虽然从统计的角度来说，样本容量越大，计量结果可能越精确，但具体到VaR的计量，却未必如此。样本规模越大，意味着要往前追溯的时间越长，历史越久远。虽然历史模拟法是假设历史可以模拟未来，但基于常识判断，历史越久远，对现实和未来的影响可能就越弱，因此历史模拟法的样本规范一般都不会太大。

在基于随机游走模型的蒙特卡罗法下，样本来自于对未来情景的直接模拟生成，理论上说，这个样本的容量可以是无限大的。一般也要求样本容量足够大，至少要以万次为单位，动辄百万、千万甚至亿万次。比如在本实验中，我们模拟了10000次，那么，得到的样本容量就是10000个数据。理论上讲，通过这样大容量地反复模拟，对未来可能结果的覆盖面就越宽，而历史模拟法由于样本容量有限，覆盖面相应也就有限。

一般来说，如果样本期间，股票价格呈显著的单边上扬（或下跌）的趋势，用基于随机游走模型的蒙特卡罗法计量出来的VaR会明显大于（或小于）历史模拟法计算出来的VaR。

三、总结

VAR方法表示处于风险状态的价值，此处应用在皖通高速股票上，用三种方法计算在99%置信水平下，该投资者的最大损失。其中历史模拟法概念直观、容易计算，能够有效地处理非对称和肥尾等问题。但是，历史模拟法假设市场因子在未来某个时间段里的变化与过去某个时间段的变化完全相同，这与现实金融市场的变化不完全吻合。蒙特卡罗方法快速简单，省却了复杂的数学推导和演算过程，但是蒙特卡洛模拟法必须输入一个随机数，如果随机数输入不合理，将会影响整个实验结果。参数法尽管计算结果较为准确，但是其通常适用正态分布。三种方法下，计算得到的皖通高速的风险价值都高于6000元，这充分说明投资风险较大，应理性投资，合理分配资产。