基于发展学生数学核心素养目标的基本不等式的备考策略

张丽丽

(江苏省南京市第五高级中学 210000)

在高中教学过程中，教师会重点强调基本不等式解题步骤为“一正、二定、三相等”，但是在实际解题中学生会犯错误，这就容易在整个过程中丢失分数.在此背景下，如何引导高中生把握基本不等式的本质，搞清楚解题技巧，如何提升他们的数学核心素养，从而在做题过程中不丢分甚至少丢分就变得非常重要.

一、注重基础，稳拿分数

数学知识来源于日常生活，但是经过数学家抽象化、符号化后的内容变得抽象、难以理解，这就很难深入开展高中数学教学.在教学过程中，广大数学教师不妨把基本不等式与其几何意义进行连接，使学生了解和掌握它的成立条件，从而对知识进行外延，加深他们对基本不等式相关知识的理解.一般而言，凑项法是基础的基础，教师要引导学生在拿到题目后观察不等式，将其配凑(凑项、凑系数等)成符合其条件.

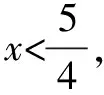
解析第一步，根据观察已知函数的表达式，通常不符合基本不等式成立的三个条件“一正二定三相等”，将其配凑(凑项、凑系数等)成符合其条件.

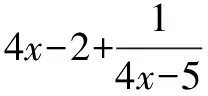
第二步，使用基本不等式对其进行求解即可.

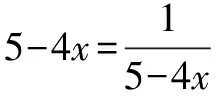
第三步，得出结论.

故当x=1时，ymax=1.

点评本题需要调整项的符号，又要配凑项的系数，使其积为定值.

二、适度拔高，熟练应用

在高考试卷中，绝大多数的数学试题属于中等难度试题，教师在学生掌握基础知识之上进行适度拔高很有必要.在教学过程中，教师要精选一些数学试题，通过精讲、精炼来达到适度拔高和拓展目的，从而确保高中生在考试中不丢分数，拿到大多数的分数.最值问题涉及到基本不等式的求解，学生要观察函数的表达式特征，将其分子或分母一次形式视为一个整体来进行凑项.

解析第一步，首先观察已知函数式特征，如分子(或分母)是二次形式且分母(或分子)是一次形式.

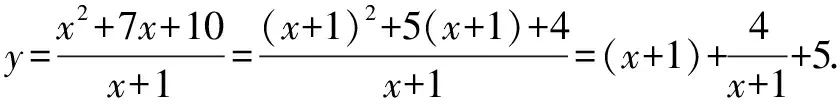
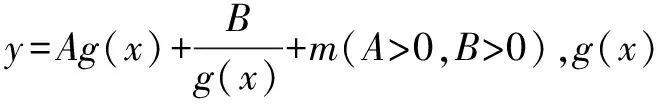
通过中等难度试题的练习，学生能够了解高考考查难度，增强应对高考的信心.

三、克服难题，综合运用

在很多高考试卷中，基本不等式会和其它知识点进行有机结合作为大题甚至是压轴题出现，这大大提升了试题的难度.对于此类问题，教师在教学中不能放弃，要引导学生进行综合分析，找到试题关联的知识点，对问题进行剖析找到本质，从而提升解决问题的综合能力.在日常训练中，学生经常会遇到函数与基本不等式结合求值域的问题，此时，在凑项、应用不等式的基础上还要结合函数单调性来进行求解，此类问题难度较大.

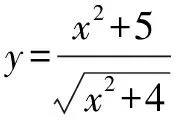
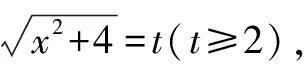
第二步，运用基本不等式并检验其等号成立的条件，若等号取不到则进行第三步，否则，直接得出结果即可：

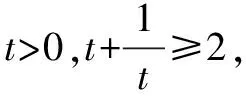
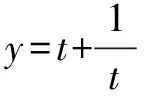
第四步，得出结论.

针对难度较大的试题，教师要引导学生深入探究，采取多个角度进行分析，找到问题背后的知识点，学会应用知识寻找问题的切入点.

总之，基本不等式在高中数学教学中占据非常重要的地位，也是学生学习的难点和重点，教师要帮助他们在理解和掌握的基础上灵活运用相关知识，把握内在的数学本质，最终为学习其它数学知识点来打下坚实的基础，也为获取高考的高分增添一份保障.