轴承-轴承座系统振动特征与局部故障尺寸的关联*

刘 静 , 徐子旦， 唐昌柯， 王林峰

(1.重庆大学机械传动国家重点实验室 重庆，400044) (2.重庆大学机械工程学院 重庆，400044)

引 言

轴承-轴承座系统是旋转机械设备的重要基础部件之一。当其内部轴承出现故障时，将严重影响机械设备的工作性能、可靠性和安全性。据统计，30%的旋转机械故障和44%的大型异步电机故障是由轴承故障导致的[1]。为了保证重要关键装备运行的可靠性和安全性，需要开展轴承-轴承座系统内部轴承早期局部故障的准确定量诊断方法研究。实际中由于工况复杂、载荷多变及非线性接触界面等因素的影响，轴承-轴承座系统内部轴承早期局部故障的冲击机理及其振动特征尚待深入研究。

针对轴承-轴承座系统内部轴承早期局部故障诱发的振动特征问题，学者们开展了许多研究工作。目前，主要的建模方法包括集中质量建模方法、准静态建模方法、准动态建模方法、动力学建模方法和有限元建模方法等[2]。作为准确的建模方法之一，有限元建模方法被许多学者应用于滚动轴承局部故障诱发的振动特征仿真分析[3]。李国超等[4]建立了三维滚动轴承外圈裂纹有限元模型，将外圈裂纹故障对轴承接触应力和振动特征的影响规律进行了仿真。王华庆等[5]建立了三维滚动轴承局部故障有限元模型，分析了套圈典型局部故障诱发的轴承的加速度信号振动特征。Liu等[6]建立了二维圆柱滚子轴承有限元模型，研究了局部故障边缘形貌特征对单个轴承振动特征的影响规律。Zhang等[7]建立了三维球轴承有限元模型，分析了局部故障诱发的滚道故障边缘的应力集中现象。Singh等[8]建立了二维圆柱滚子轴承有限元模型，讨论了外圈滚道局部故障对轴承内部接触力及其振动特征的影响规律。文献[4-8]主要集中考虑轴承内部局部故障诱发的自身振动特征，然而在实际工程中，传感器一般布置在轴承座的外表面，轴承内部局部故障诱发的振动波将沿轴承和轴承座传播衰减，从而导致轴承的振动特征可能出现变化。因此，文献[4-8]的研究难以描述轴承内部局部故障诱发的轴承座的振动特征。

针对轴承内部局部故障诱发的振动波将沿轴承和轴承座传播衰减的问题，学者们进行了大量研究。王彬等[9]建立了二维准动态球轴承有限元模型，分析了局部故障位置分布对轴承振动特征分布形态的影响规律以及局部故障的振动信号沿轴承外圈和轴承座的传递特性。Yuan等[10]建立了轴承-轴承座系统集中质量模型，研究了轴承内部局部故障诱发的系统振动特征。Ahmadi等[11]建立了滚动轴承-轴承座系统动力学模型，分析了轴承内部局部故障尺寸对其振动特征的影响规律。Xiao等[12]建立齿轮-轴-轴承-轴承座系统动力学模型，研究了内部冲击激励沿齿轮-轴-轴承-轴承座系统的振动传递特性。Liu等[13]建立了轴-轴承-轴承座系统动力学模型，分析了轴承内部局部故障冲击激励对轴承-轴承座系统振动特征的影响规律。虽然以上研究工作采用有限元法和集中质量建模方法讨论了轴承内部冲击激励的沿轴承-轴承座系统的振动传递特性，但是文献[9-13]采用准动态有限元方法、动态有限元方法和集中质量法，分析了轴承内部冲击激励诱发的轴承-轴承座系统的振动特征变化规律，尚未深入分析局部故障尺寸与轴承-轴承座系统内部动态冲击力及其振动特征之间的关联关系。文献[11]虽然建立了滚动轴承-轴承座系统有限元模型，将轴承座考虑为简化结构，但无法准确描述局部故障尺寸与轴承座不同测点的振动特征之间的关联关系。

针对上述问题，笔者采用显示动力学有限元分析方法，综合考虑了圆柱滚子轴承-轴承座系统的弹性结构、重力以及轴承内部摩擦力的影响，建立了含局部故障的圆柱滚子轴承-轴承座系统有限元模型，研究了轴承外圈滚道表面不同尺寸的局部故障诱发的轴承-轴承座系统振动特征演变规律，分析了局部故障尺寸与轴承-轴承座系统振动特征之间的关联关系。

1 含局部故障的轴承-轴承座系统模型描述

图1(a)为含局部故障的轴承-轴承座系统示意图。该系统由轴承内圈、外圈、保持架、滚子和轴承座组成。假设局部故障位于轴承外圈滚道表面。实际中，当滚动体经过局部故障区域时，滚动体将与局部故障始边和末边发生两次冲击激励，诱发轴承-轴承座系统产生异常振动[14-15]。

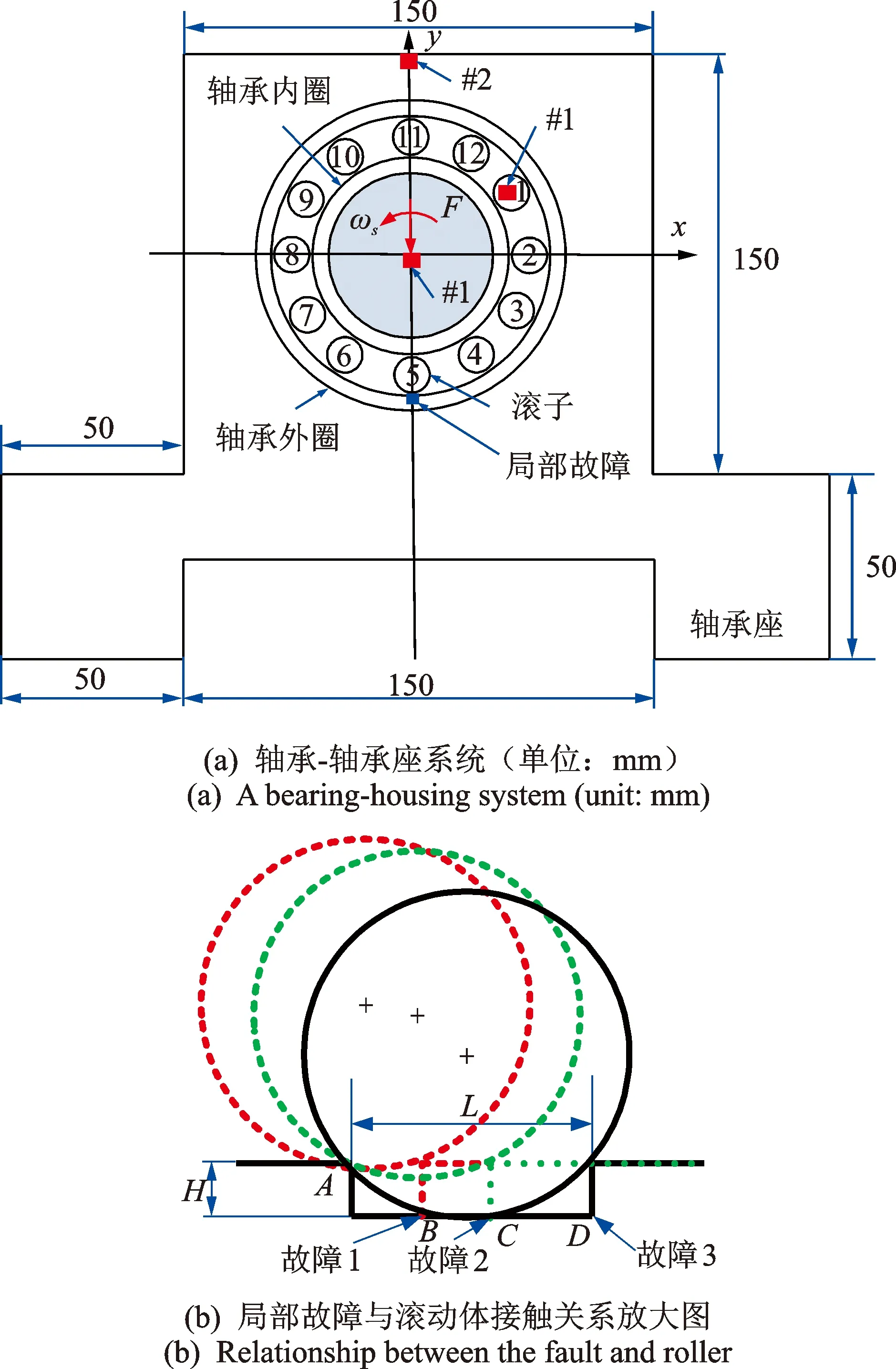
图1 含局部故障的轴承-轴承座系统示意图Fig.1 Schematic of a bearing-housing system with a localized fault

如图1(b)所示，当局部故障尺寸不同时，滚动体通过局部故障区域时，滚动体将分别与故障1、故障2和故障3的B，C和D处发生冲击碰撞。图1(b)显示，3种不同局部故障尺寸情况下，滚动体与局部故障边缘发生两次冲击激励的间隔长度分别为AB，AC和AD。可见，3种不同局部故障尺寸情况下，滚动体通过局部故障过程中诱发的冲击波形及其冲击时间也各不相同。针对这一问题，笔者建立含局部故障的轴承-轴承座系统有限元模型，研究不同尺寸的局部故障诱发的轴承-轴承座系统内部冲击力及其振动特征。

2 显示动力学有限元分析方法的动力学方程

显示动力学有限元分析方法的动力学方程[16]为

(1)

其中：M为轴承-轴承座系统的质量矩阵；Fi为轴承-轴承座系统内部作用力向量；Fc为轴承-轴承座系统的阻尼力向量，其计算表达式为CΔl/Δt；C为黏性阻尼系数向量;Δl为有限元模型中单元长度的变化量；Δt为有限元模型的计算步长；Fa为轴承-轴承座系统的外载荷向量；s为轴承-轴承座系统的位移向量。

显示动力学有限元分析方法通常采用中心差分法求解式(1)中的轴承-轴承座系统的动力学方程。该方法运用前一步的速度向量和中间速度向量计算当前计算步的中间速度向量，其表达式为

(2)

其中：t为时间。

同时，该方法利用速度-时间积分法获取计算步的起始位移向量，求解该计算步结束时刻的位移向量，其表达式为

(3)

为保证结果的计算精度和稳定性，采用的计算时间步长需满足Courant-Friedrichs-Levy条件，其表达式为

(4)

其中：Δtc为求解轴承-轴承座系统的有限元动力学模型时的许用计算步长；Le为系统的有限元动力学模型中的最小单元尺寸；E为系统部件材料的弹性模量；ρ为系统部件的材料密度。

3 含局部故障的轴承-轴承座系统有限元模型

以圆柱滚子轴承N306为例，建立的含局部故障的轴承-轴承座系统有限元模型包括轴承座、轴承内圈、保持架、滚动体和轴承外圈。如图1所示，在轴承内圈中心点处施加沿负y方向的径向力Fr；轴承内圈施加沿逆时针方向转速ωr。同时，模型考虑了重力的影响。为保证计算过程的稳定性，径向力和重力由0 ～0.005 s线性增加至恒定值，再经过0.005 s的稳定阶段后，从0.01～0.015 s线性施加转速至恒定值。施加径向力和重力是为了消除初始游隙，保证滚动体发生转动前能够与轴承套圈处于接触状态，实现轴承的正常运转。其中，径向力、重力和转速采用线性变化的加载方式，消除了加载过程诱发的冲击对系统振动响应的影响，以获得更可靠的计算结果。滚动体与保持架兜孔之间的间隙为0.1 mm，轴承径向游隙为0.02 mm。轴承座的几何尺寸如图1所示。轴承内圈滚道直径为40.5 mm，外圈滚道直径为62.5 mm，滚动体直径d为11 mm，节圆直径dm为51.5mm，滚动体长度为11.4 mm，滚动体个数Z为12。选取局部故障为贯穿式矩形故障(即故障宽度等于外圈宽度)，其位置位于外圈。根据文献[6,8]的研究结果，为保证计算结果的准确性，轴承和轴承座的材料模型均可定义为线弹性材料模型，其材料的弹性模型、泊松比和密度分别取为200 GPa，0.3和7 850 kg/m3；滚动体与滚道之间以及滚动体与保持架之间的接触特性采用库伦摩擦力模型进行建模，根据文献[5-8]的研究结果，定义动摩擦因数为0.005，静摩擦因数为0.1。轴承-轴承座系统各部件采用二维平面应变单元进行建模。轴承-轴承座系统有限元模型的阻尼定义为2%。

建立的含局部故障的轴承-轴承座系统有限元模型如图2所示。有限模型的单元总数为390 835，单元最小尺寸为0.1mm。单元网格的划分依据主要包括：a.保证滚动体与滚道之间接触区为高质量的四边形网格，在接触区以外的部分也尽可能采用四边形网格，减小模型中三角形单元的数量，以保证三角形网格数目占模型单元总数的比例小于5%；b.结合式(4)中的计算步长，在保证计算精度的前提下尽可能增大计算步长，减小计算时间和计算资源。

图2 含局部故障的轴承-轴承座系统有限元模型Fig.2 A finite element model of a bearing-housing system with a localized fault

4 计算结果与分析

选取径向外载荷Fy为2kN(沿y负方向)，内圈的转速Nin为1 800 r/min(沿逆时针方向)。提取图1中不同位置的2个测点的振动信号进行对比分析。图1中，测点1位于内圈中心，用于获取轴承内圈的振动信号；测点2位于轴承座顶部中心点，用于获取轴承座的振动信号。

4.1 模型验证

为了验证所建立的有限元模型的有效性，将有限元模型获得的正常轴承的保持架转速与文献[17]获得的理论值进行对比分析，如图3所示。图3中轴承保持架转速ωc的中间值约为73.89 rad/s。根据文献[17]的计算方法，保持架转速的理论计算值为74.12 rad/s(ωc=0.5(πNin/60)(1-d/dm))。结果显示，有限元模型的仿真结果与理论计算方法之间的差异为0.31%，表明所建立的有限元模型的有效性。

为了进一步验证模型计算结果的正确性，将有限元模型获得的正常轴承测点1的加速度响应频谱特征与利用文献[17]的方法获得的结果进行对比分析，如图4所示。图4中，测点1的加速度响应频谱中存在特征频率30.53，140.4和219.7 Hz。该特征频率分别与运用文献[17]的方法计算获得的内圈旋转频率30 Hz(Nin/60)、外圈通过频率141.55 Hz((ZNin/(2×60))(1-d/dm))和内圈通过频率218.45 Hz((ZNin/(2×60))(1+d/dm))接近，表明所建立有限元模型的正确性。

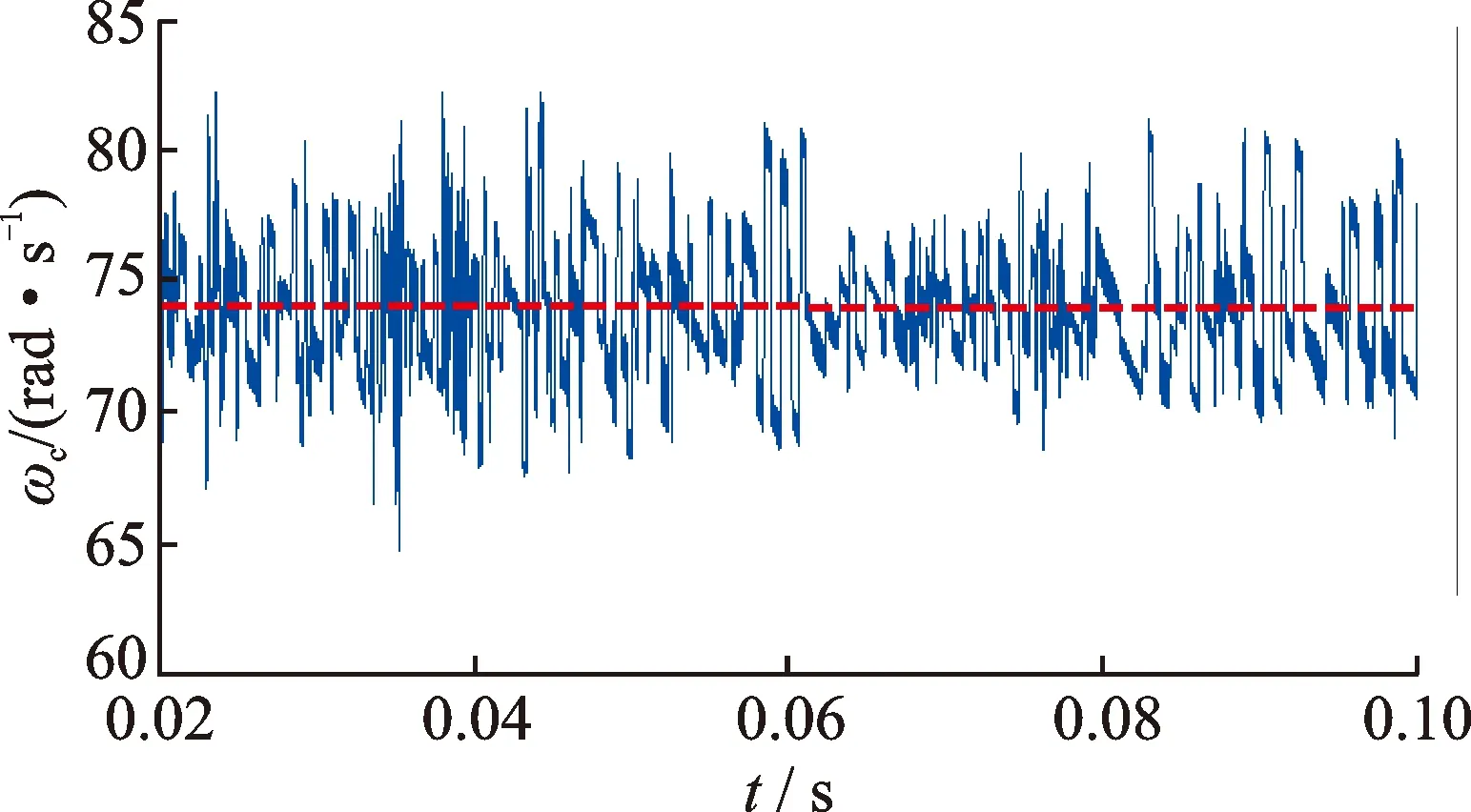
图3 正常轴承保持架角速度Fig.3 Rotation velocity of the cage of the healthy bearing

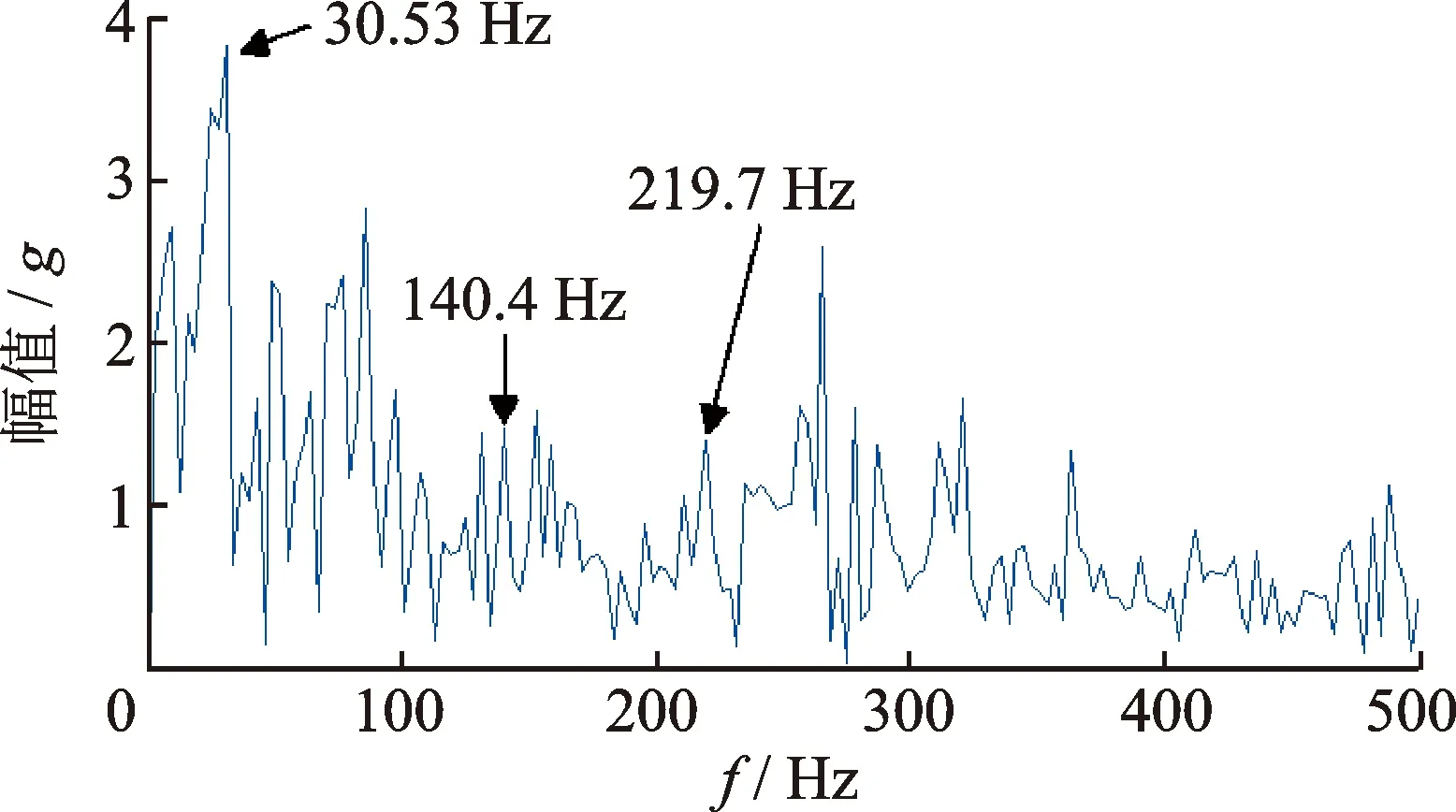
图4 测点1的加速度响应频谱Fig.4 Spectra of the acceleration of point #1

4.2 故障长度对滚子与滚道接触力的影响

选取故障长度L分别为1，3和5mm，深度H为0.2 mm。图5为故障长度对滚子#1与滚道之间接触力的影响。图5(a)显示，滚子进入和退出载荷区的过程中，滚子与滚道之间的接触力先逐渐增大再逐渐减小；当滚子位于如图1所示的轴承载荷区的中间位置时，滚子与滚道之间的接触力达到最大值；故障对滚子与外圈滚道之间接触力的幅值和波形均有较大影响；滚子与滚道之间的接触力存在周期性波动，该波动主要由其余滚子进入或退出载荷区以及轴承振动引起。

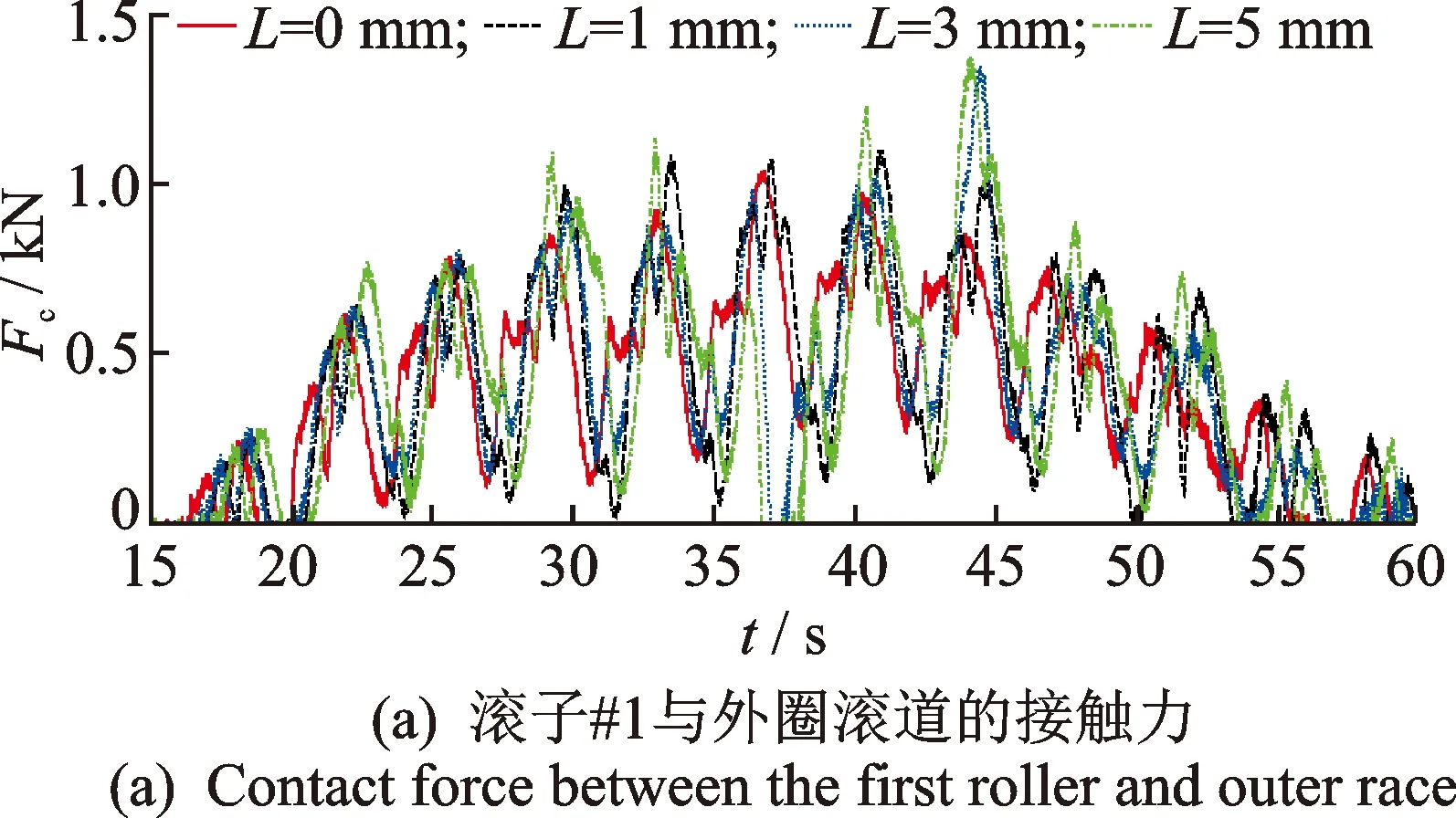
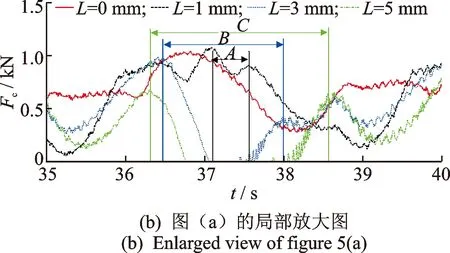
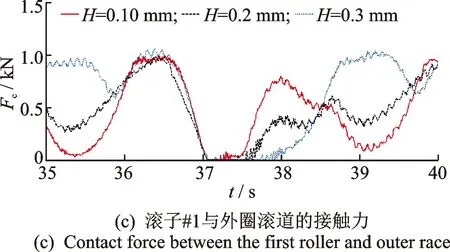
图5 故障对滚子#1与滚道之间接触力的影响Fig.5 Effect of defect on contact force between the roller and race

图5(b)显示了滚子#1通过故障区域时，滚子#1与外圈滚道之间接触力的局部放大图。图5(b)表明，滚子#1进入故障区域时，滚子#1与外圈滚道之间的接触力将逐渐变小；当滚子#1位于故障中心位置时，滚子#1与外圈滚道之间的接触力达到最小值，当滚子#1与故障的末边接触时，滚子#1与外圈滚道之间的接触力逐渐增大；当故障长度L=1 mm时，滚子#1通过故障区域时的接触力冲击波形为连续时变波形，其形态与正弦函数波形较为接近，如图5(b)所示的区域A；当故障长度L=3 mm和5 mm时，滚子#1通过故障区域时的接触力冲击波形包括连续时变冲击波形和连续时不变冲击波形，分别如图5(b)中的区域B和C所示。图5(b)中，L=3 mm时，对于滚子#1与外圈滚道之间接触力中的冲击波形区域B，当滚子#1进入故障区域时，接触力逐渐减小，该过程的接触力冲击波形为连续时变冲击波形；当滚子#1完全进入故障区域时，接触力的值变化至约为0 kN，直至滚子#1与故障区域的末边发生接触，该过程的接触力冲击波形为连续时不变冲击波形；滚子#1与外圈滚道之间的接触力降至约为0 kN，其原因为故障的尺寸较大导致滚子进入故障区域的几何深度大于其余滚子与滚道之间的接触变形，使得滚子#1与内圈之间出现了未接触的情况；当滚子#1接触故障末边直至离开故障区域时，该过程的接触力冲击波形为连续时变冲击波形。图5(b)中，L= 5 mm时，滚子#1与外圈滚道之间的接触力中的冲击波形区域C与区域B的变化情况相似，均由连续时变冲击波形和连续时不变冲击波形部分组成。图5(b)中，当故障长度L=3 mm和5 mm时，滚子#1通过故障区域产生的时变接触力冲击波形区域B和C的形态可以认为是由正弦函数和矩形函数组成的复合函数波形。同时，图5(b)显示，滚子#1退出故障区域诱发的接触力的冲击波形变化明显大于滚子#1进入故障局域导致的接触力的变化。该现象说明，滚子退出故障区域诱发的滚子与滚道之间的冲击力大于滚子进入故障区域时导致的冲击力；滚子进入故障区域引起的轴承振动水平小于滚子退出故障区域诱发的轴承振动水平。

图5(c)为故障深度对滚子#1与外圈滚道之间接触力的影响。选取故障长度L为3mm。图5(c)显示，故障的深度对滚子与外圈滚道之间的接触力幅值和波形也存在较大影响；其中，故障深度对滚子进入故障区域时接触力的影响小于其对滚子退出故障区域时接触力的影响。

图6为载荷和内圈转速对滚子#1与滚道之间接触力的影响。图6(a)显示，滚子#1和外圈滚道之间接触力的幅值随径向外载荷的增大而增大，然而径向外载荷对滚子#1和外圈滚道之间接触力的波形影响较小；滚子#1与故障末边接触力的波动幅值随载荷增大而有所减小。图6(b)和(c)显示，滚子#1和外圈滚道之间接触力的幅值随内圈转速的增大而增大；然而，内圈转速对滚子#1和外圈滚道之间接触力的波形影响较小；滚子#1与故障之间接触力的持续时间随内圈转速增大而减小。

表1为不同故障条件下滚子#1通过故障区域的时间对比情况。表1中，滚子通过故障区域的时间td等于故障外圈滚道圆周方向的圆周角除以滚子通过外圈滚道表面的角速度。从表1可知，采用有限元模型所获得的滚子#1通过故障区域时间的仿真值与利用理论计算方法获取的理论值之间存在一定差异，且随着故障长度L的增大而呈现增大的趋势。其原因是有限元模型中滚子与故障边缘之间存在弹性接触变形，而理论计算方法未考虑该因素的影响。上述计算结果表明，滚子与故障边缘之间的弹性接触变形对滚子通过故障区域的时间会产生一定影响，因此采用滚子通过故障区域时间为指标的轴承故障定量诊断方法需要考虑该因素的影响，以提高轴承故障诊断方法的准确性。

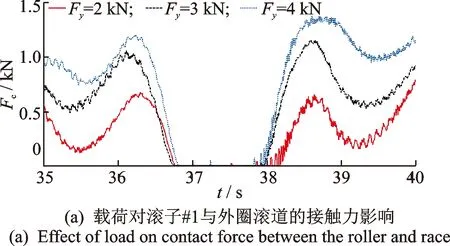
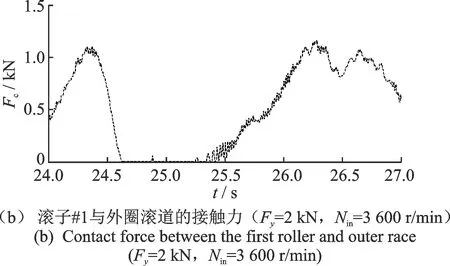
图6 载荷和内圈转速对滚子#1与滚道之间接触力的影响Fig.6 Effects of load and rotational velocity of inner race on contact force between the roller and race

Tab.1 Comparisons of time during the processing of the roller passing over the defect

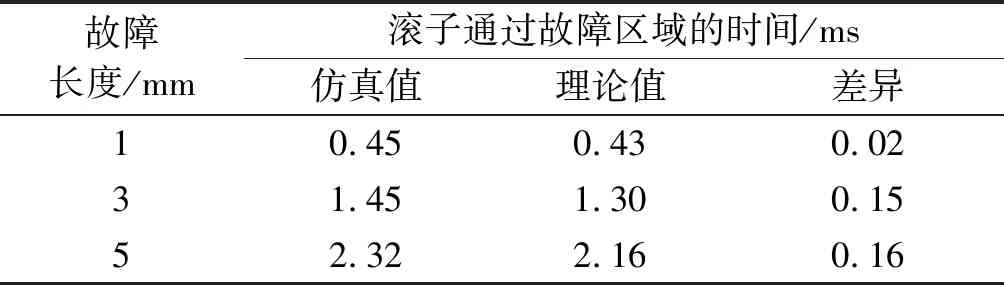
故障长度/mm滚子通过故障区域的时间/ms仿真值理论值差异10.450.430.0231.451.300.1552.322.160.16

4.3 故障长度对轴承-轴承座系统振动响应的影响

选取故障长度L分别为0, 1，3和5mm，深度H为0.2 mm。其中，L=0 mm，为无故障轴承。图7为无故障轴承与外圈滚道含故障的轴承的滚子#1沿y方向的时域振动加速度响应(ar)对比分析图。图7显示，故障轴承滚子#1的振动加速度的幅值大于无故障轴承滚子#1的振动加速度的幅值；滚子#1通过故障区域时，滚子的振动加速度存在明显的冲击激励，且该冲击激励的幅值随故障长度L的增大而增大，如图7中区域A，B和C所示。图6(b)显示，当故障长度L=1 mm时，滚子#1的振动加速度响应中存在冲击激励S1(区域A)，该冲击激励的波形为连续时变波形，与图5(b)的区域A的结果类似，其形态也与正弦函数波形较为接近；结果表明，该故障工况诱发的滚子振动加速度响应的冲击激励可认为是呈正弦函数形态的连续冲击波形。图7(c)显示，当故障长度L=3 mm时，滚子#1的振动加速度响应在区域B存在两处冲击激励S2和S3。冲击激励S2和S3分别是由滚子#1进入和退出故障区域引起的。其中，冲击激励S3的幅值和持续时间均大于冲击激励S2的幅值和持续时间，其原因是故障末边诱发的冲击力大于故障起始边(图5(b)所示)。从图7(d)可知，当故障长度L=5 mm时，滚子#1的振动加速度响应在区域C同样存在两处冲击激励S4和S5。其中，冲击激励S5的幅值和持续时间均大于冲击激励S4的幅值和持续时间，其原因与图7(c)中叙述的原因一致。上述振动加速响应中冲击激励形态特征可为轴承故障的准确定量诊断提供有益的参考。

图8为故障尺寸对轴承-轴承座系统中测点1(轴承内圈选取点)和测点2(轴承座选取点)处振动加速响应的均方根值的影响规律。图8显示，测点1和测点2的振动加速度响应的均方根值值均随故障长度和深度尺寸增大而增大，测点2的均方根值大于测点1。上述结果表明，轴承内部的振动波传递到轴承座时，其振动能量将出现衰减现象。

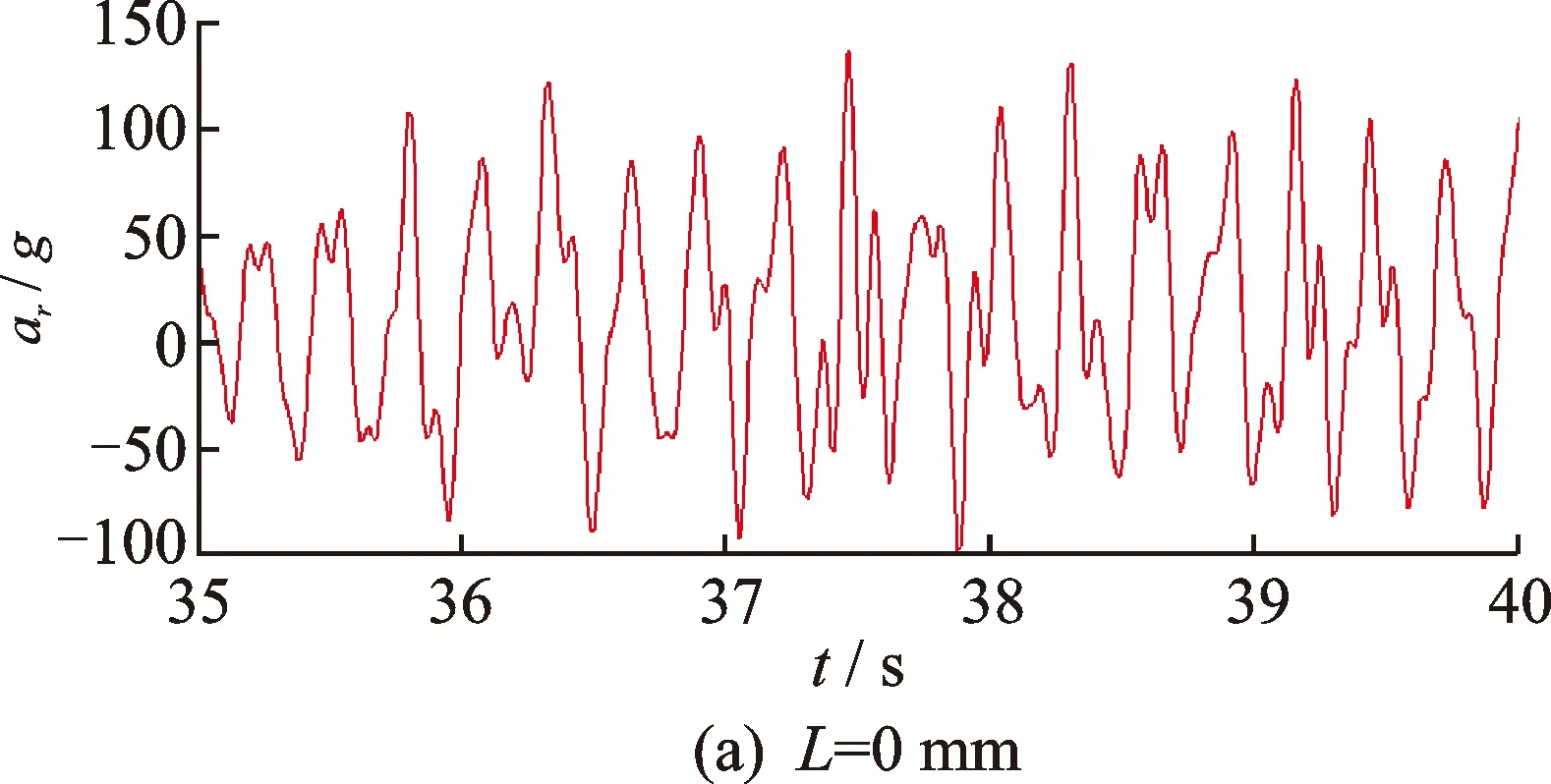
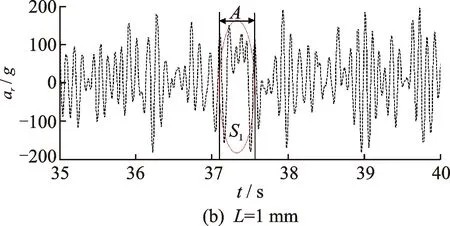
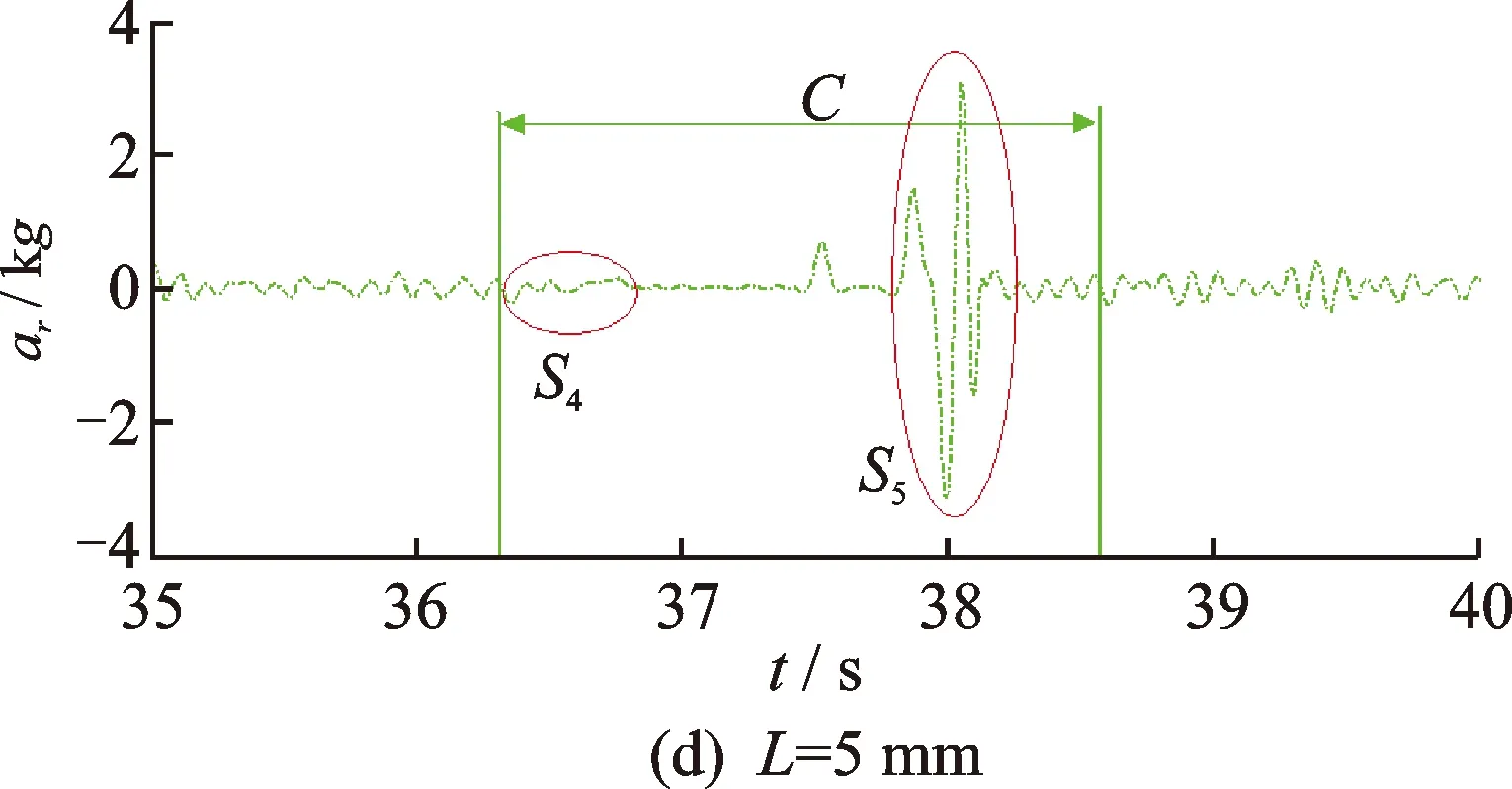
图7 故障长度对滚子#1加速度响应的影响Fig.7 Effect of defect on acceleration of the first roller

图8 故障尺寸对轴承-轴承座系统加速响应的均方根值影响Fig.8 Effect of defect size on the root mean value of accelerations of the bearing-housing system

5 结 论

1) 以圆柱滚子轴承-轴承座系统为研究对象，综合考虑其各部件的弹性变形、重力和轴承元件之间的接触与摩擦的影响，建立含局部故障的轴承-轴承座系统有限元动力学模型，研究不同尺寸的局部故障诱发的轴承-轴承座系统的振动特征；分析局部故障尺寸变化对系统振动特征的影响规律。

2) 滚子进入和退出载荷区的过程中，滚子与滚道之间的接触力先逐渐增大再逐渐减小；当滚子位于轴承载荷区的中间位置时，滚子与滚道之间的接触力达到最大值。

3) 局部故障对滚子与外圈滚道之间接触力的幅值和波形均有较大影响。当局部故障尺寸较小时，故障诱发的时变接触力可认为是呈正弦函数形态的连续冲击波形；当局部故障尺寸较大时，故障诱发的时变接触力形态可以认为是由正弦函数和矩形函数组成的复合函数波形；滚子退出局部故障区域诱发的滚子与滚道之间的冲击力大于滚子进入局部故障区域时导致的冲击力。

4) 当局部故障尺寸较小时，故障诱发的滚子振动加速度响应的冲击激励呈正弦函数形态的连续冲击波形；当局部故障尺寸较大时，故障诱发的振动加速度形态在滚子进入和退出故障区域时存在双峰现象；滚子退出局部故障区域诱发的滚子与滚道之间的振动加速度大于滚子进入局部故障区域时导致的振动加速度。