MBCV-EWT和奇异值差分谱的滚动轴承信号降噪方法*

2019-08-28王亚萍葛江华李云飞

振动、测试与诊断 2019年4期

王亚萍，崔巍，葛江华，许迪，李云飞

(哈尔滨理工大学机械动力工程学院哈尔滨，150080)

引言

当机械设备运行时，由于现场环境及工况变化等因素的影响会导致信号中会掺杂大量的噪声，同时也会引起动态信号出现非平稳性。这些非平稳信号的统计量是时变函数，需要通过时频分析方法处理信号，常用的有Wigner-Ville分布、经验模态分解和小波变换[1-3]等，但是以上方法存在欠包络、过包络和模式混叠等问题。

为了克服传统信号分解中的问题，Gilles[4]提出经验小波变换(empirical wavelet transform，简称EWT)方法，可以自适应划分初始信号的频谱，同时通过相对应的带通滤波器在各自的划分区间内构造正交带通滤波器组，以此提取具有紧支撑的调幅-调频分量。Aneesh等[5]分别用变分模态分解与EWT对电能质量进行分类并做对比。Thirumala等[6]将EWT用于电能质量指标(power-quality indices，简称PQIS)的估计。为了验证EWT与传统方法的差异，国内学者将EWT应用于转子，并与经验模态分解(empirical mode decomposition，简称EMD)、集合经验模态分解(ensemble empirical mode decomposition，简称EEMD)等方法进行对比，证明了EWT的有效性[7-10]。EWT方法中最核心的部分是信号频谱的划分，划分后的区间影响后续信号分解的效果，文献[11]对经典划分方法进行了阐述。祝文颖等[12]提出了一种单分量个数的估算方法用于频谱划分，给出了敏感信号分量选取方法，仍存在EWT区间定位模糊的问题。划分后的调幅-调频分量较多，缺乏寻优过程，需要建立一个筛选指标来挑选最优的分量，而无量纲指标基本不受工况、载荷和转速等变化影响的特点为此提供了新的思路[13]。

为了进一步实现故障特征的提取，需要先对噪声干扰进行抑制。Jumah等[14]提出基于小波变换系数取阈值的方法，该方法对去除一维高斯白噪声具有较好效果，但不能改进小波变换理论不足的缺点。Imaouchen等[15]将互补集合经验模态分解用于强噪声背景下信号的处理实现强制降噪，模态混叠问题依旧存在。奇异值差分谱可以识别出奇异值的最大突变点位置，通过对突变点前一系列成分的重构可以实现信号的降噪，该方法在处理分解后的分量时效果突出[16-18]。胥永刚等[19]提出双树复小波的信号分解方法，通过奇异值差分谱实现单分量的降噪，但其计算复杂，很难应用到实际生产生活中。

综上所述，针对传统EWT存在的问题，笔者提出MBCV-EWT与奇异值差分谱相结合的信号降噪方法，通过自适应的对信号频率进行划分克服模式混叠等问题，利用评价指标筛选最优调幅-调频分量并根据最大奇异值突变点实现信号的降噪。

1 最大类间方差-经验小波变换分解

经验小波变换的实质是对信号的频谱进行划分，并相应的在每个区间构造带通滤波器，实现对信号中不同的调幅-调频成分的提取，为后续降噪提供基础。

1.1 多域多类别故障特征提取

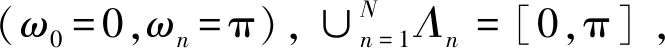
最大类间方差(maximum between-cluster variance，简称MBCV)[20-22]通过计算目标与背景的类间方差并将最大值作为图像划分阈值的标准。对于给定图像，假设像素数为N，灰度取[0,L-1] ，则

(1)

其中：ni为素数；pi为像素点出现的概率，pi=ni/N,i=0,1,…,L-1。

图像根据阈值K分为目标c0和非目标c1两部分，分别为灰度值在[0,k]和[k+1,L-1]中的像素构成，图像的均值表示为

(2)

c0与c1的均值为

(3a)

(3b)

类间方差表示为

w1(c1-ck)2=w0w1(c0-c1)2

(4)

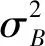
为了提高MBCV的自适应性，引入P作为循环结束的判定准则确定阈值的数量，P的取值范围为[0，1] ，即

(5)

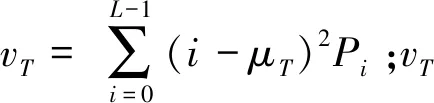
P越大，表明类间的差别越大，当P近似于1时，类间方差为最大值，可以确定阈值数，自适应的区间就被划分出来。

1.2 构建区间内的带通滤波器

确定了每个区间的边界之后，模仿小波变换的方式在区间上构造带通滤波器，根据2π的周期性只研究区间[0，2π]，可以得到

(6)

在Tn不重叠的情况下也同样适用于τn，即

τn+τn+1<ωn+1-ωn⟺γωn+γωn+1<

(7)

经验小波变换的细节系数为

(8)

经验小波变换的近似系数为

(9)

得到经验模态函数为

(10a)

(10b)

1.3 调幅-调频分量筛选指标

有量纲分析的故障诊断主要是从时域方面进行分析，主要包含均值、均方根值和方差3种幅域参数，有量纲指标对故障程度反映较为敏感，通常用于中度至重度损伤的故障诊断与预测，受外部环境影响较大，且易受复合故障的影响。

无量纲指标是根据有量纲指标的比值转化而来，反应频率密度函数的形状，对于时间序列信号X={xi},i=1,2,…,n，笔者应用无量纲幅域参数，例如：波形指标Sf、峰值指标Cf、脉冲指标If、裕度指标CLf和峭度指标Kr。

无量纲的优点可归纳为：a.完全具有反映故障特征的能力；b.几乎与振动信号绝对水平无关；c.对不同类型故障存在不同敏感性；d.对复合并发故障不敏感；e.基本不受工况、载荷和转速等变化的影响。

2 基于奇异值差分谱的调幅-调频分量降噪

MBCV-EWT分解后得到的分量通过脉冲指标选取最优的调幅-调频分量，并引入奇异值差分谱降噪方法。令信号矩阵为X=[x(1),x(2),…,x(N)]，对其进行奇异值分解及奇异值差分谱去噪。

构造Hankel矩阵为

(11)

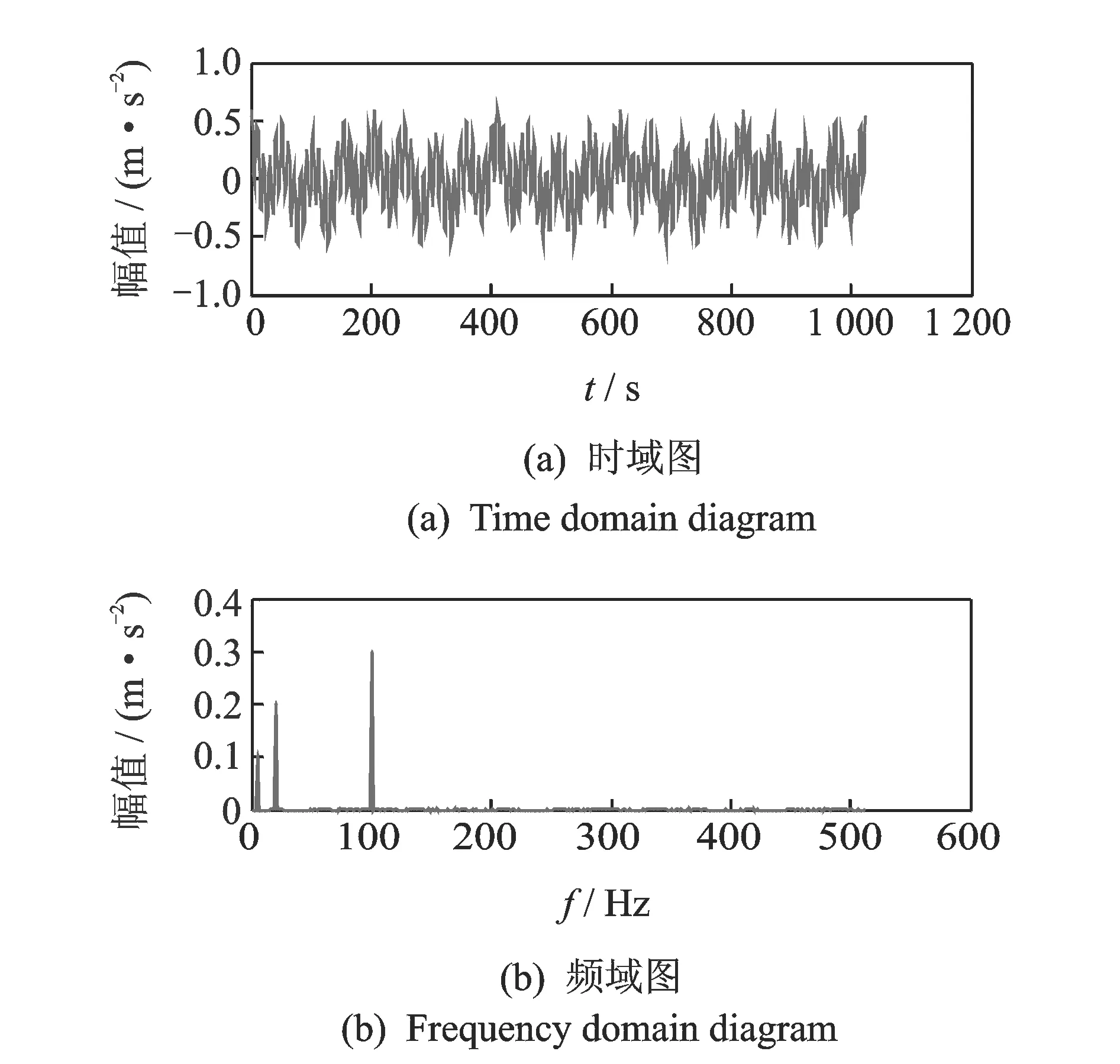
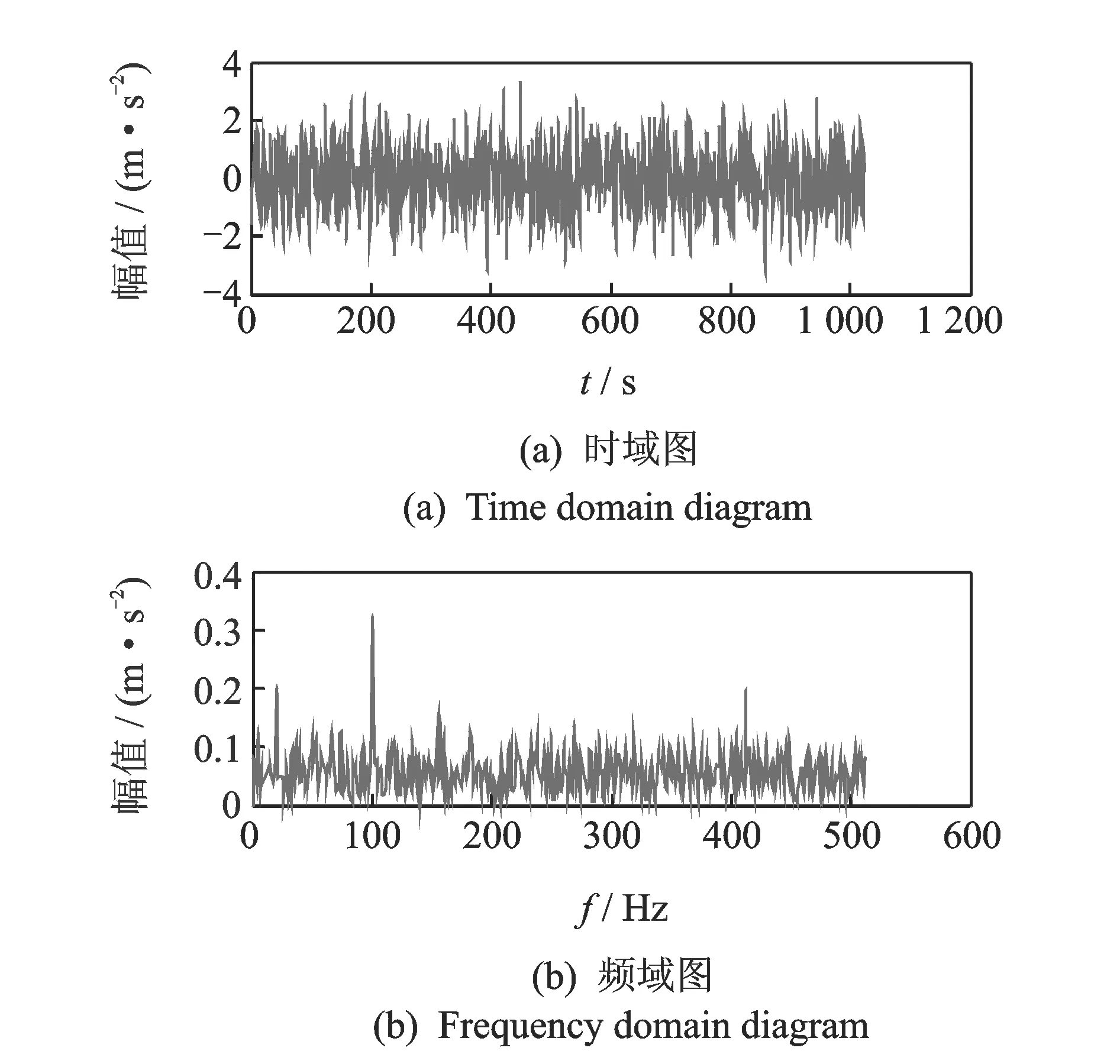
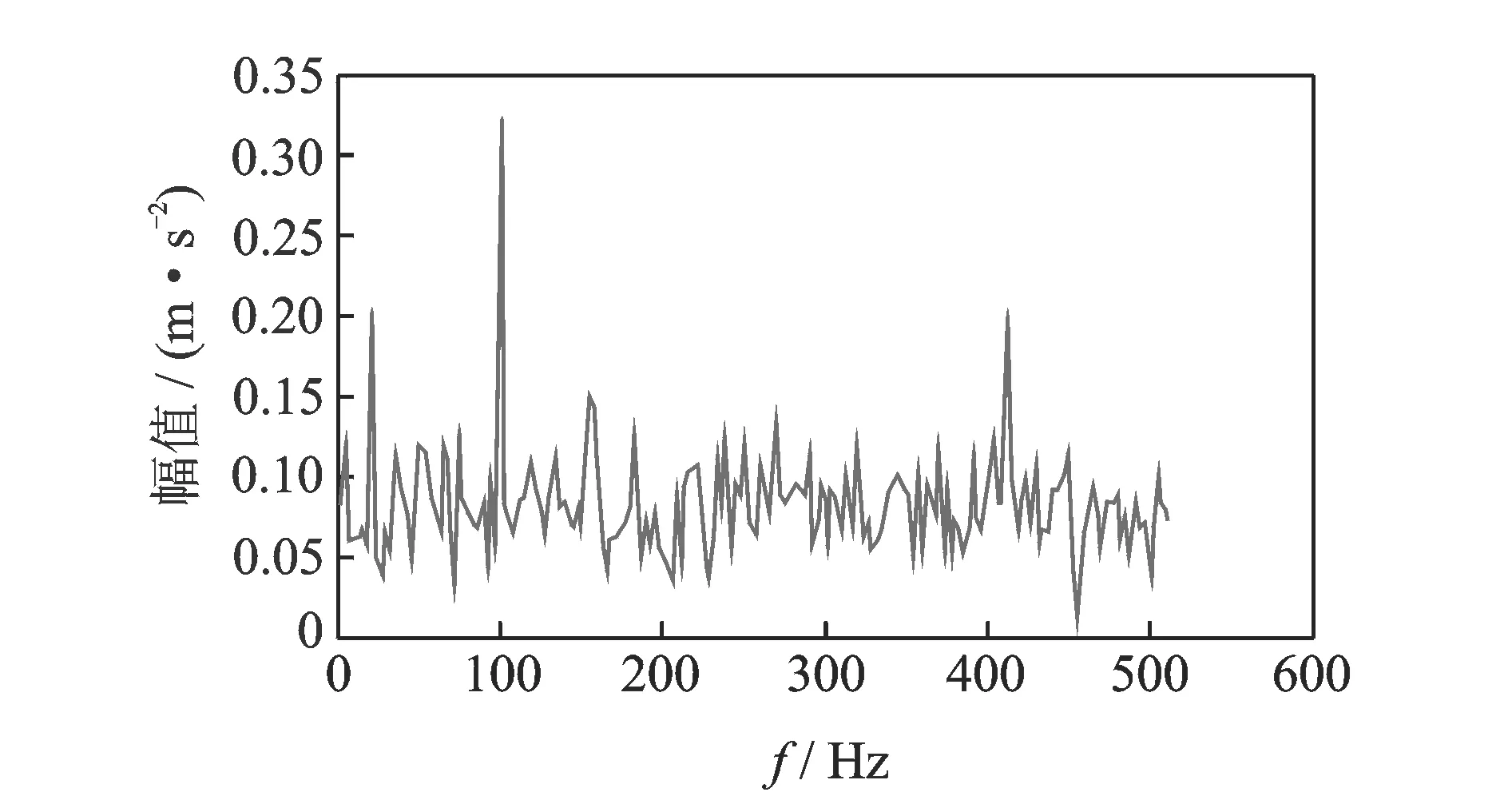
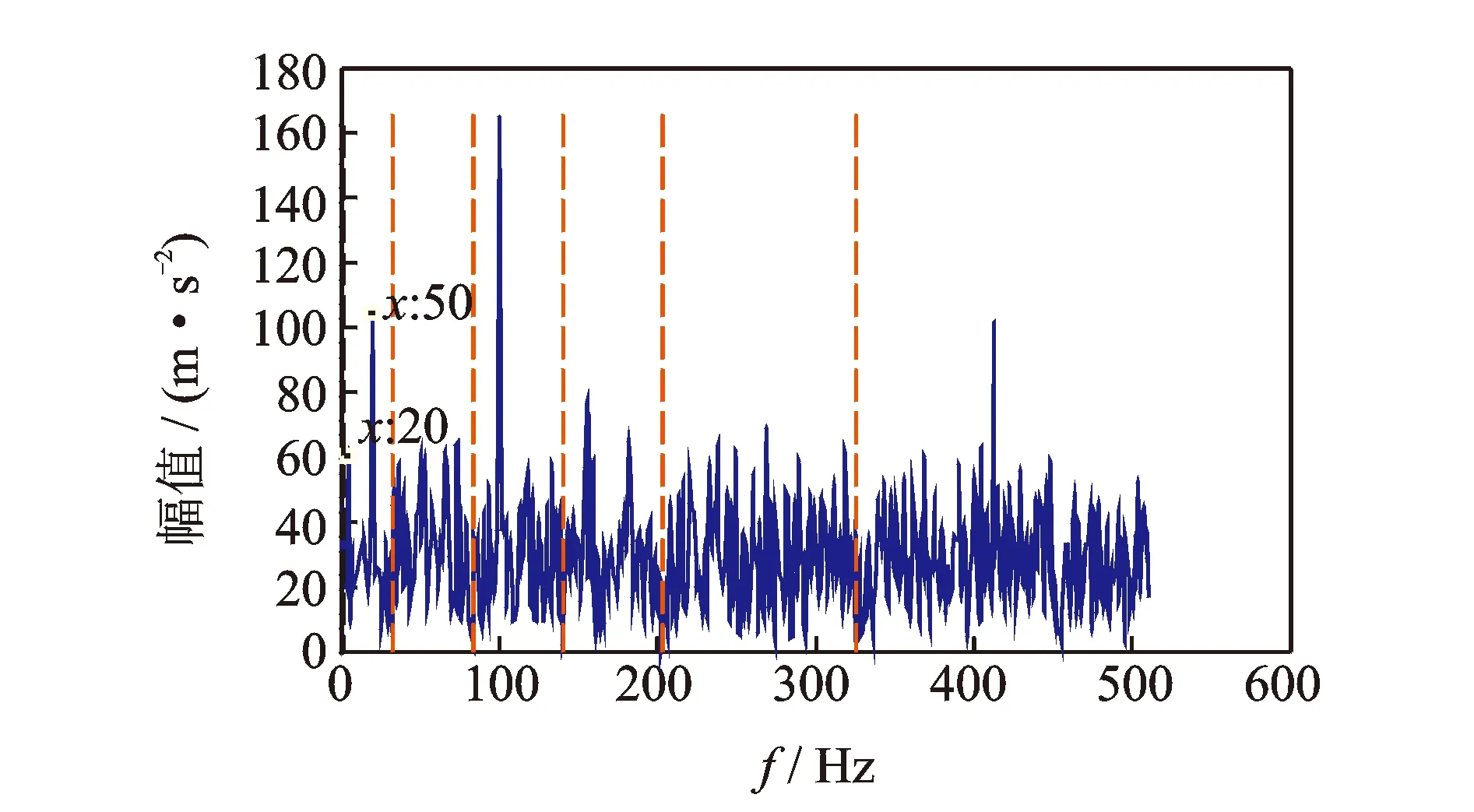
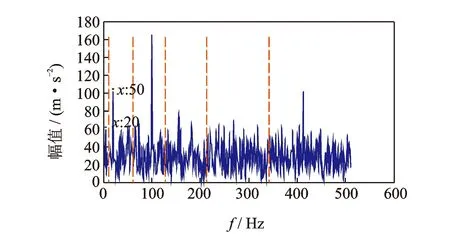
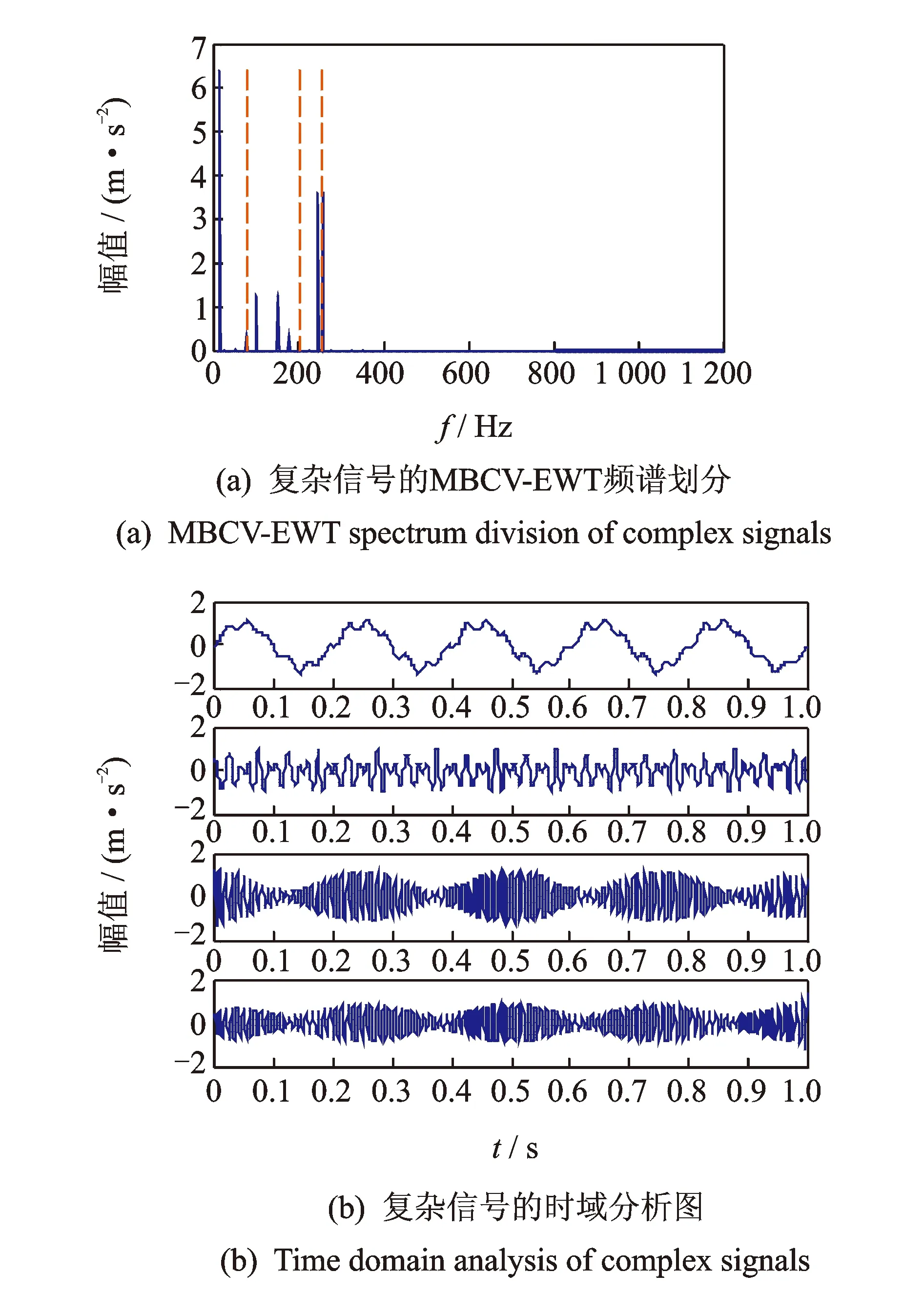
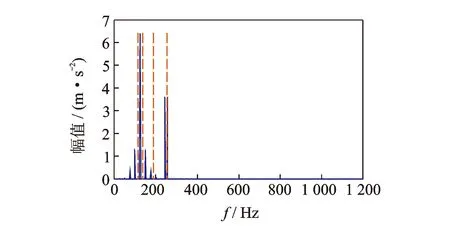
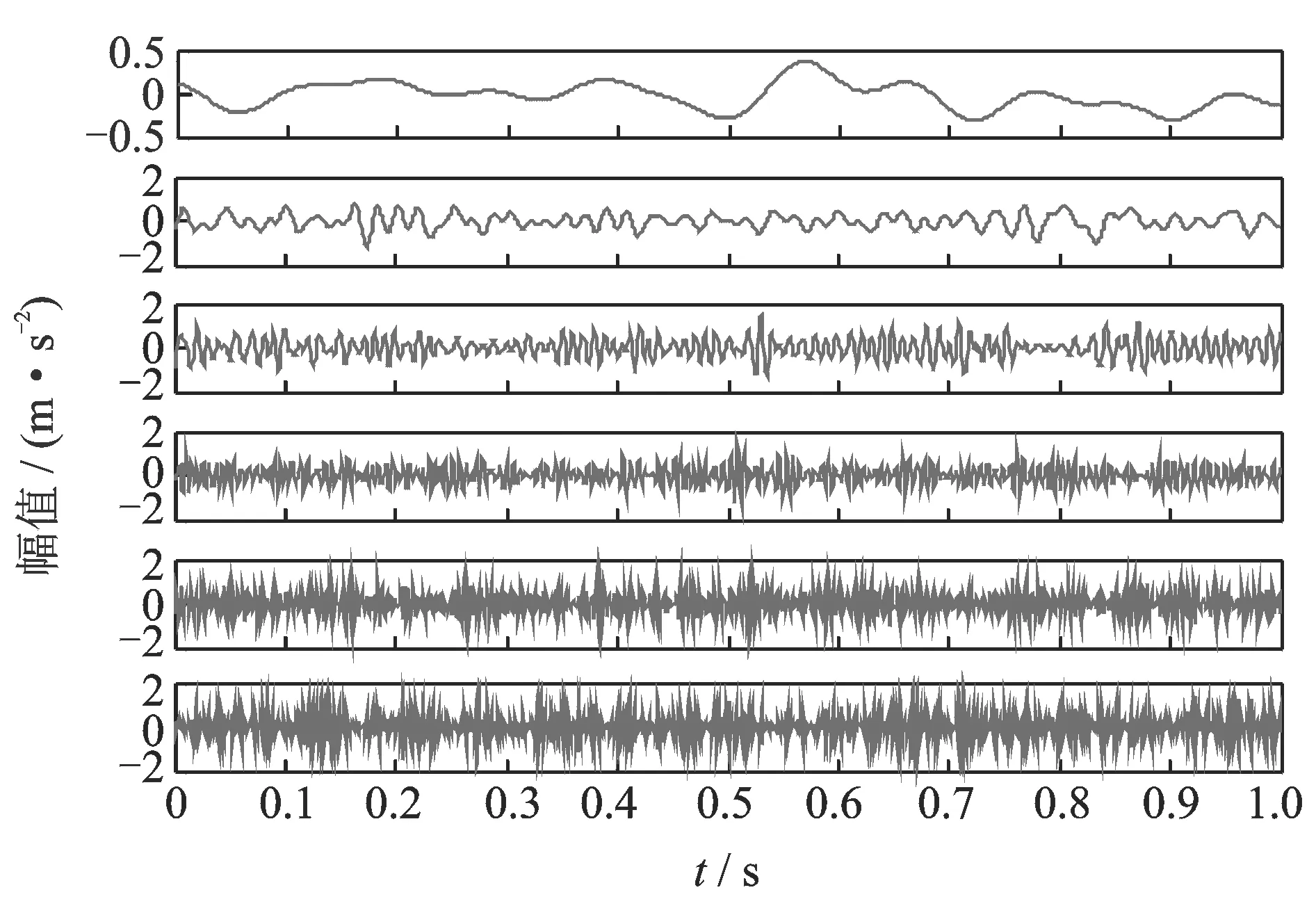
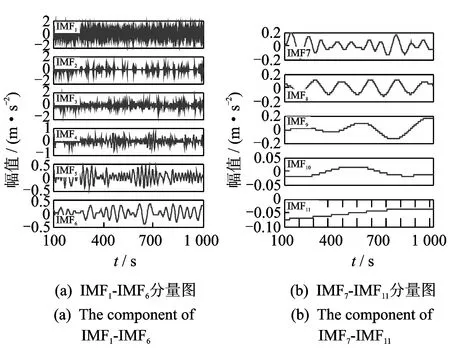
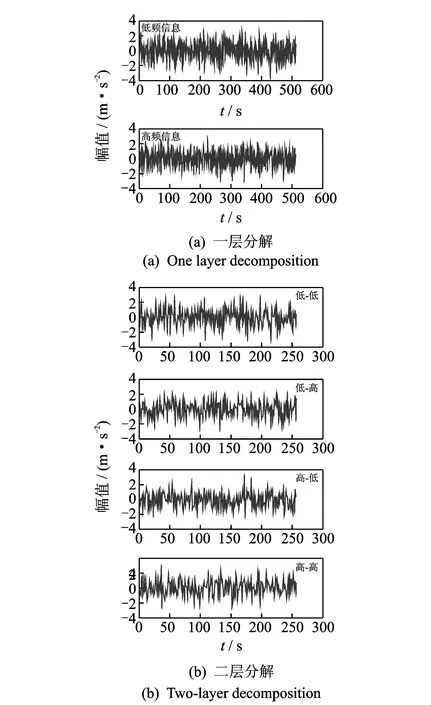
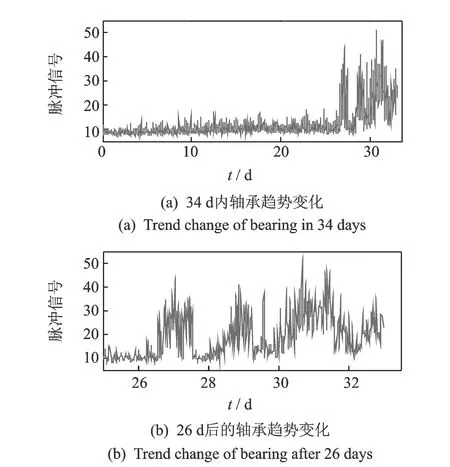
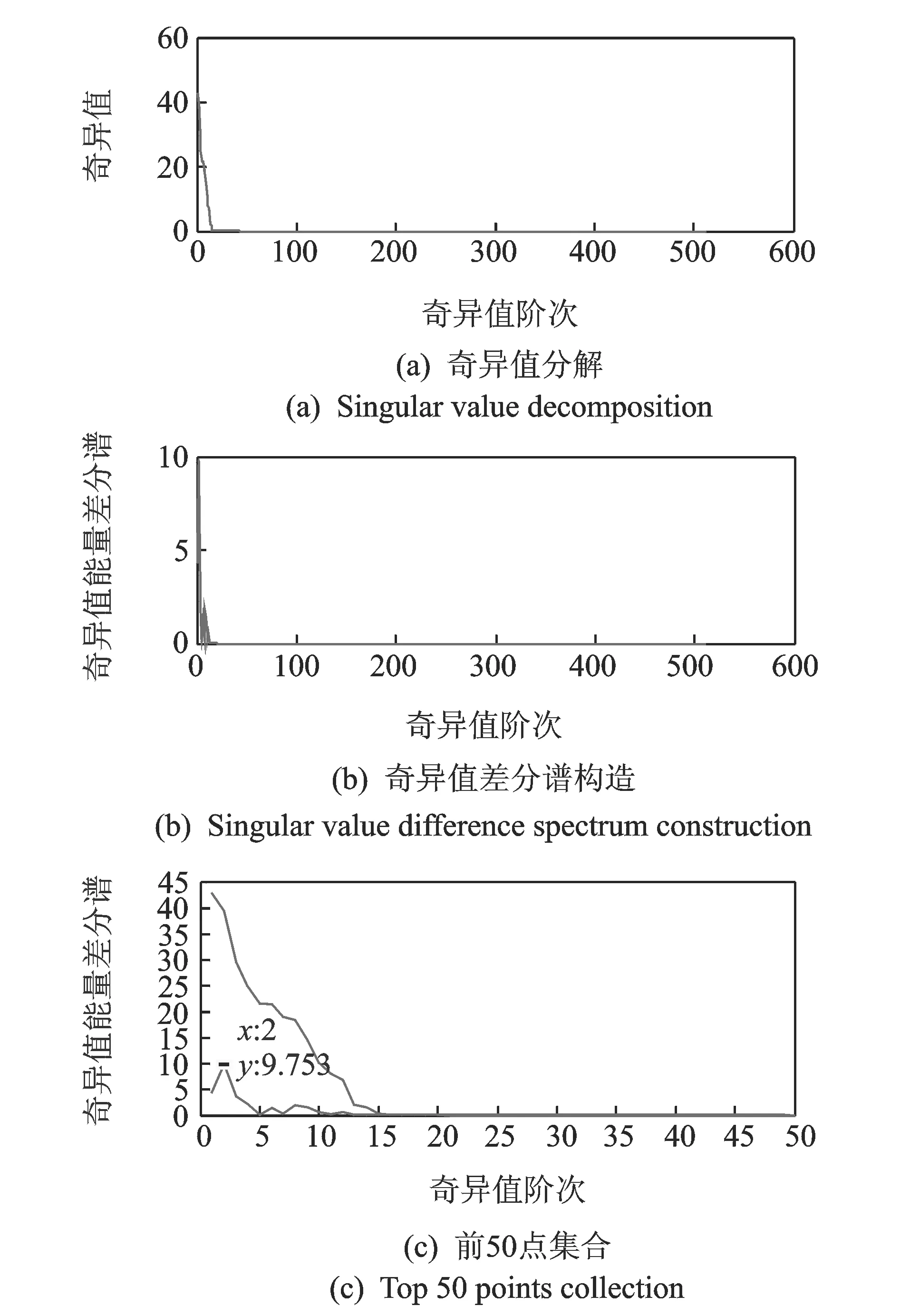
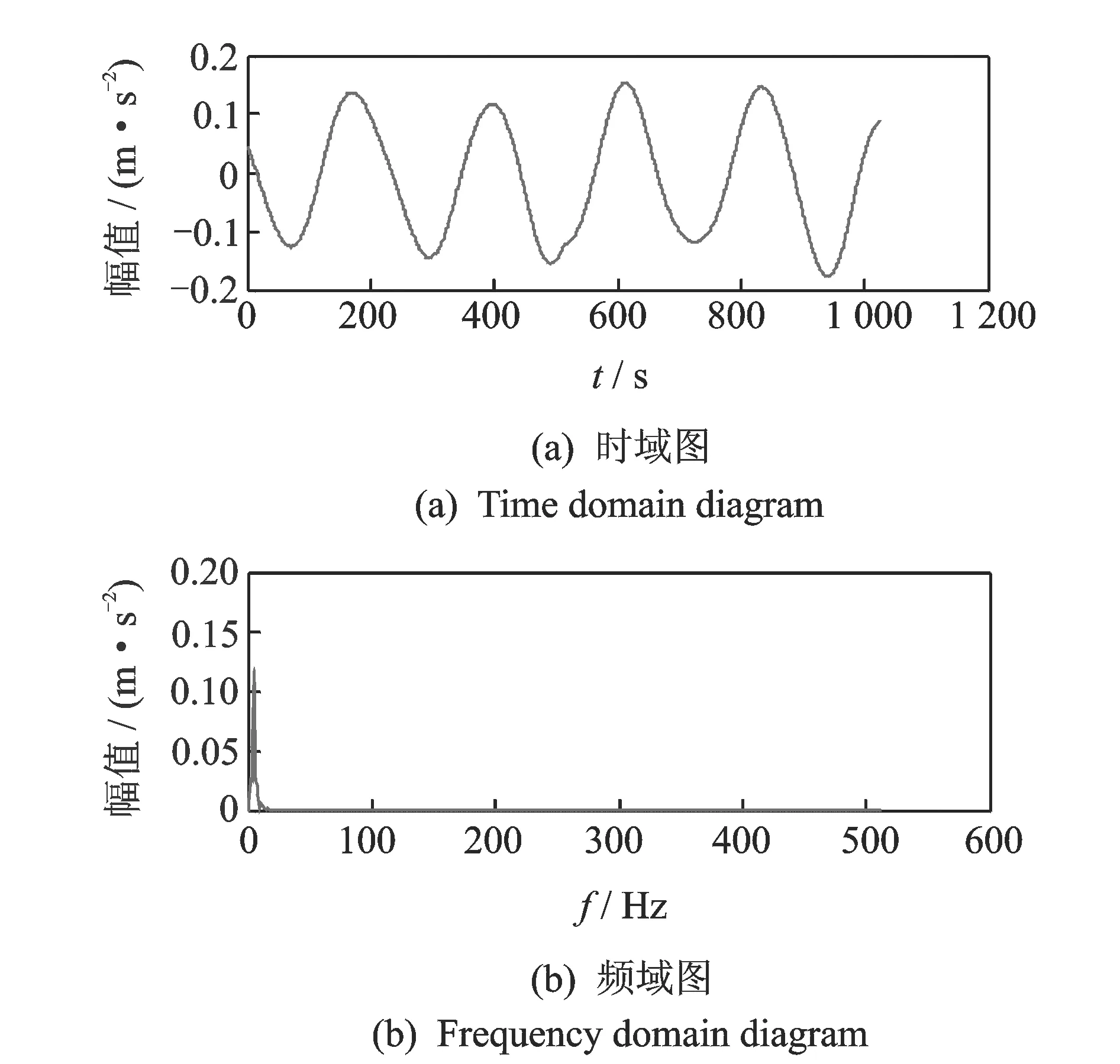
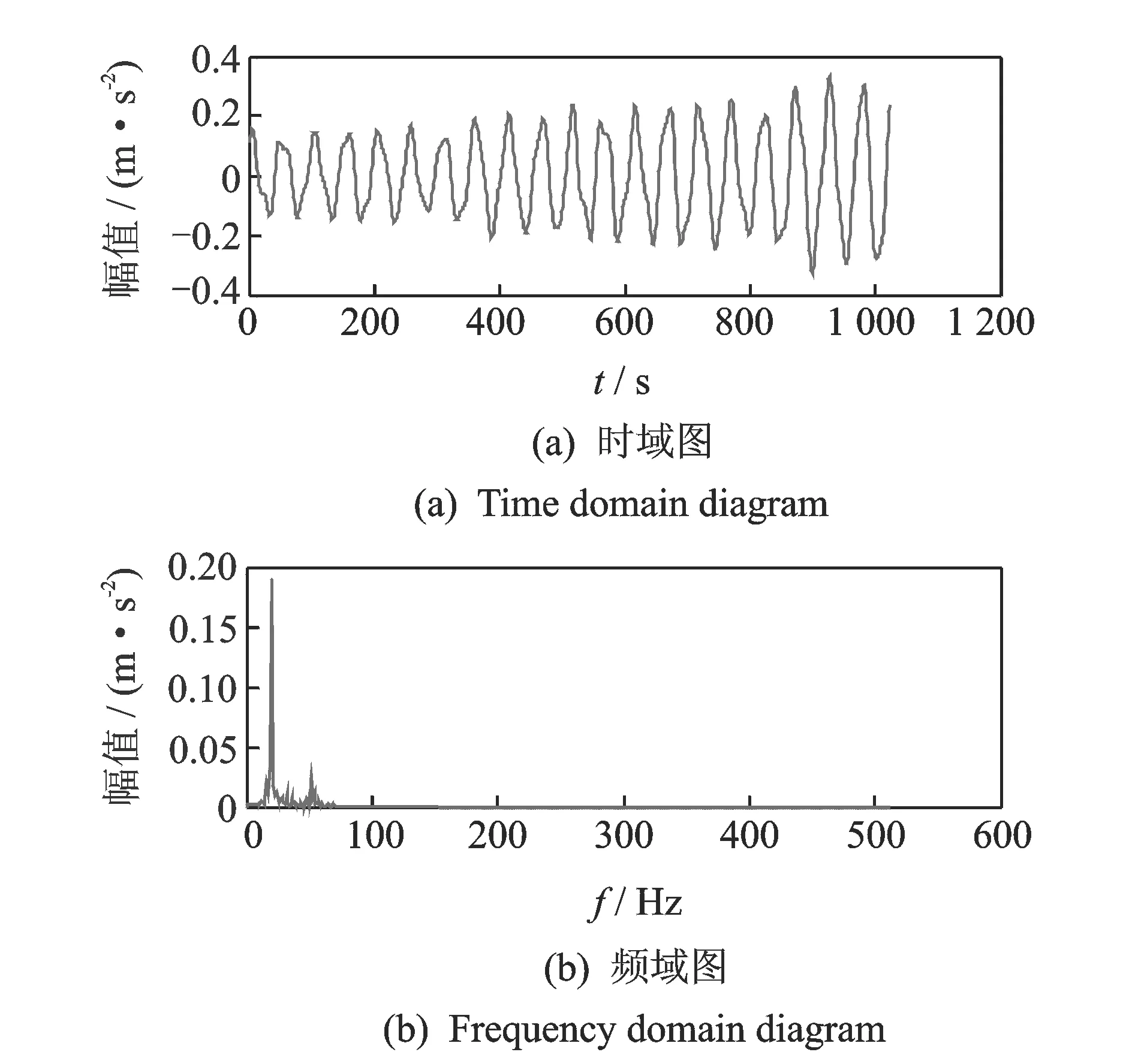
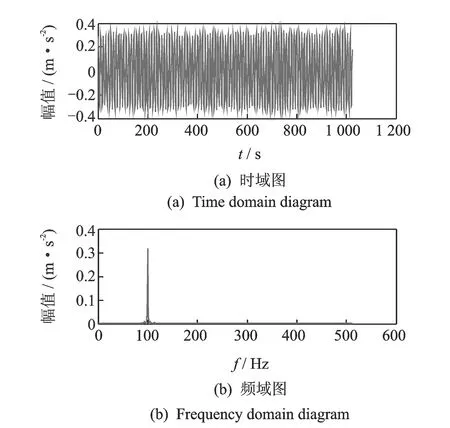
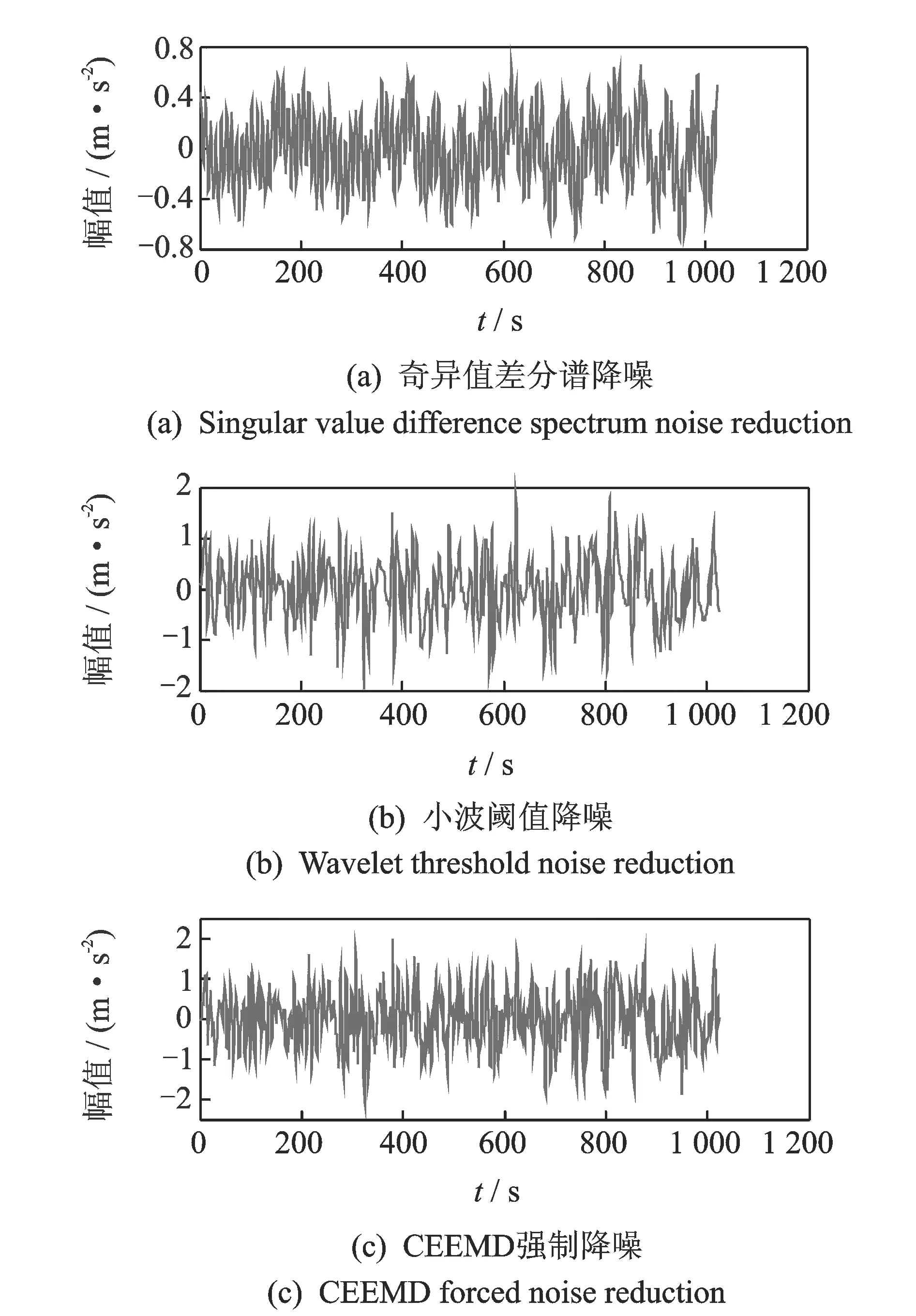
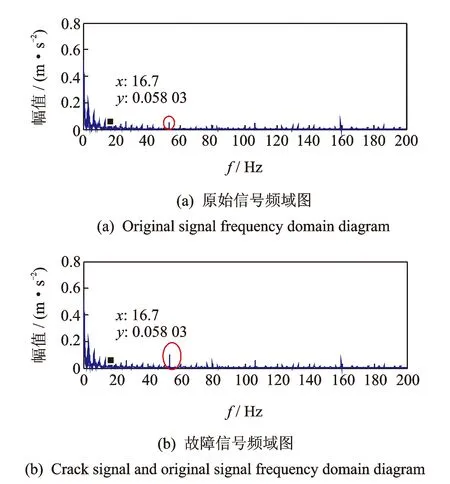
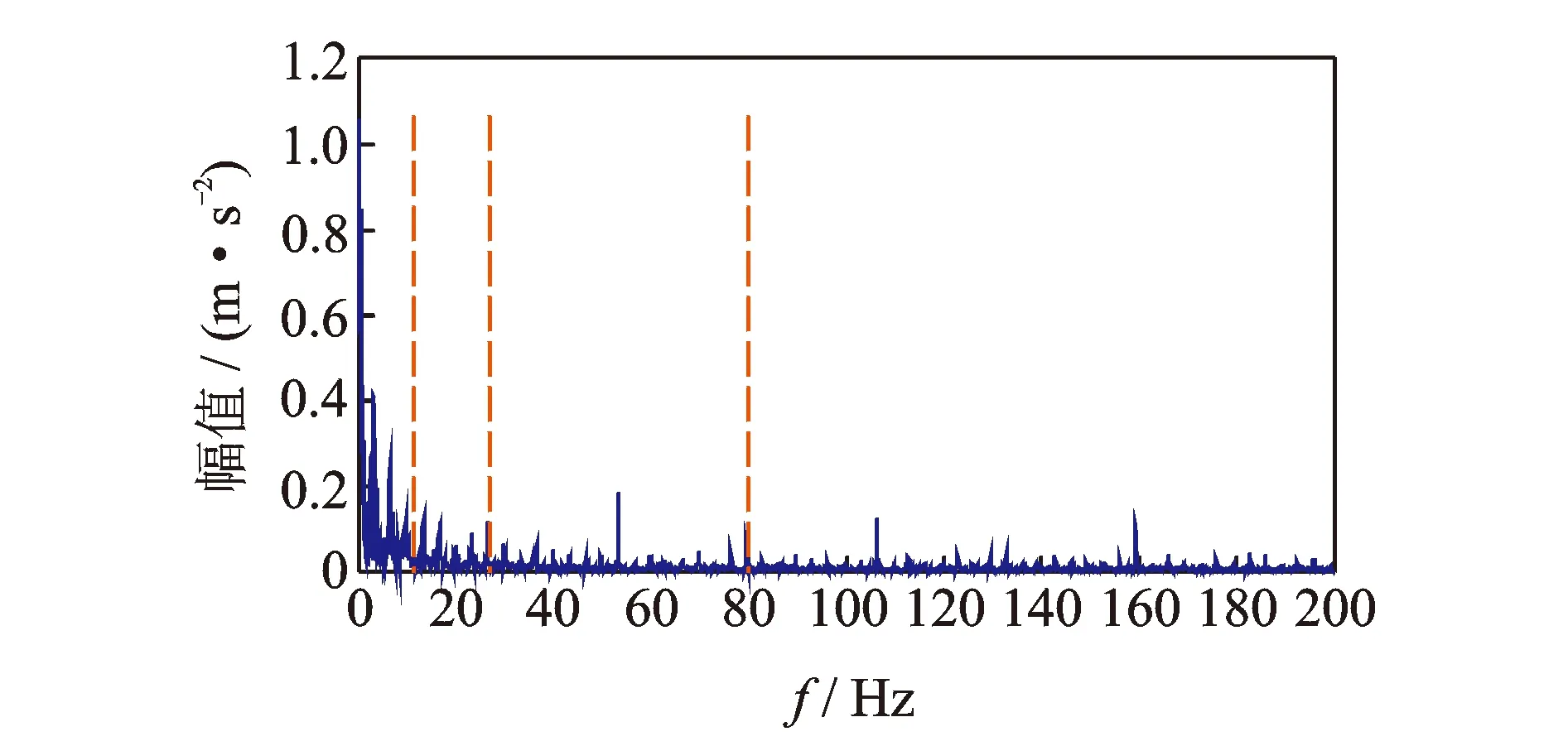
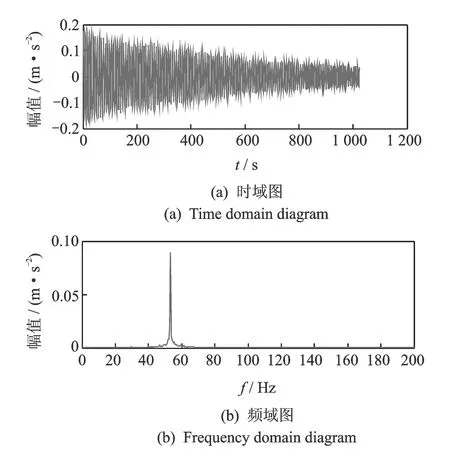
其中：1

令m=N-n+1，A∈Rm×n，则矩阵A为Hankel矩阵，即重构吸引子轨道矩阵。可以看出, Hankel矩阵相邻两行的矢量存在一定联系，后一行滞后一个位置，有用信号矩阵的奇异值特点为数值较大的集中在前端，矩阵秩对应点处差距巨大，之后的奇异值趋近于零。当矩阵中存在零奇异值，则该矩阵必然不满秩，即为奇异矩阵，其误差矩阵E的范数为零，而噪声矩阵为满秩均值，行矢量互不相关。

对于吸引子轨道矩阵A∈Rm×n，无论矩阵的行和列是否相关，必然存在正交矩阵U=(u1,u2,L,um)和V=(v1,v2,L,vn)，满足

A=USVT

(12)

其中：U和V分别为矩阵A的左右奇异阵；S=(diag(σ1,σ2,L,σq),0)或其转置，这由mn决定；A∈Sm×n，0为零矩阵；q=min(m,n)，σ1≥σ2≥…≥σq≥0，为矩阵A的奇异值。

从本质上来说，奇异值分解就是将调幅调频分量分解成一组成分的简单线性叠加，成分之间不存在相位差，有用信息与噪声分别储存在不同的成分上，通过筛选成分进行重构可以实现有用信息的保留和噪声成分的去除。

集合B=[b1,b2,…,bq-1]为奇异值差分谱序列，其中，bi为相邻奇异值的差值。选择最大突变点对调幅调频分量进行重构，根据矩阵特点将其按行与列收尾连接并进行逆变换，实现调幅调频分量的重构，重构后的信号即为降噪后的有用信号。

图1 降噪流程图Fig.1 Noise reduction flowchart

定义奇异值差分谱为

bi=σi-σi+1

(13)

可以看出，集合中必然存在一个最大的峰值bk满足最大突变点的要求。最大突变点的本质是源于不同信号奇异值差别较大，有用信号通常处于前k个奇异值成分，而噪声在之后的成分中，因此最大突变点的位置就是重构调幅调频分量所需的分量数。降噪过程如图1所示。

3 仿真与实验

3.1 仿真验证

仿真实验验证了该方法的有效性，仿真信号分别由频率为5 Hz的信号x1、20 Hz的信号x2、100 Hz的信号x3和高斯白噪声n组成，信号的采样频率fs=1 024 Hz。仿真信号表达式为

(14)

原始信号幅值图及其频谱图，噪声信号的幅值图及其频谱图分别如图2，3所示。

图2 原始信号时域和频域图Fig.2 Time domain, frequency domain diagram of the original signal

图3 加噪信号时域和频域图Fig.3 Time domain and frequency domain diagram of the noisy signal

对于传统EWT方法，频谱的划分必须计算出每个边界的具体位置。首先，求出频谱幅值的极大值，如图4所示。

图4 幅值极大值点Fig.4 Amplitude maximum point

根据Mm+α(M1-Mm)

图5 EWT自适应频谱划分Fig.5 EWT adaptive spectrum division

采用MBCV对频谱进行处理，频谱划分如图6所示。可以看出，MBCV对于频谱的划分与传统方法有所区别，在5 Hz和20 Hz，20 Hz和100 Hz之间有且仅有一条边界，说明此方法可以实现准确的划分。

图6 MBCV-EWT频谱划分Fig.6 MBCV-EWT spectrum division

此外，MBCV方法并不需要计算准确的边界，根据划分区间的个数，MBCV方法可以自适应地实现边界的确定。如图7所示，当设定只划分3个区域的时候， MBCV分解后正是信号所含有的3个主频。

对于较为复杂的信号，仿真信号表达式为

x=sin(20πt)sin(100πt+cos(20πt))+

1.5cos(4πt)cos(200πt)+sin(10πt)

(15)

如图8所示，对该信号进行MBCV-EWT分解，可以看出，第1个区间内的成分即为正弦信号，第2个区间为调幅调频信号，第3个区间为调幅信号。如图9所示，当正弦信号的频率改为125 Hz时，正弦信号的主频在调幅调频信号频率之间，MBCV-EWT可以将该频率与其他频率区分开。

图7 N=3时的MBCV-EWT分解Fig.7 MBCV-EWT decomposition at N=3

图8 复杂信号的MBCV-EWT分解Fig.8 MBCV-EWT decomposition of complex signals

图9 正弦信号改变后分解图Fig.9 Decomposed graph after sinusoidal signal changed

采用MBCV-EWT，完备总体经验模态分解(complete ensemble emprirical mode decomposition,简称CEEMD)和双层小波变换对信号进行分解，如图10～12所示。

图10 MBCV-EWT分解图Fig.10 MBCV-EWT exploded view

图11 CEEMD分解图Fig.11 CEEMD exploded view

图12 双层小波变换Fig.12 Double layer wavelet transform

通过对比发现，MBCV-EWT分解后的信号与小波变换、CEEMD分解相比得到的分量更少，每个调幅-调频分量中仅含有一个主频成分，不同的分量之间不存在模态混叠现象，更不存在固定小波后再分解导致的窗固定问题。从Matlab计算速度来看，对同一个信号MBCV-EWT的速度要优于其他几种。

评价指标部分需要采用真实的全寿命周期实验，这里采用辛辛那提大学的实验数据。试验台上安装4个双列滚动轴承，实验时间为2003-10-22T 12∶06∶24～2003-11-25T 23∶59∶56，共进行了34 d，每10 min采集一次，在实验的最后阶段轴承3发生了内圈故障。通过时间变化对每个指标的表现进行计算，如图13所示，脉冲指标前26 d表现平稳，从第26 d起，两个指标的幅值都产生明显上升，说明对早期故障非常敏感，同时在失效之前都能保持较为明显的波动。

对于EWT分解后的3个调幅-调频分量，以第1个调幅-调频分量为例，其时域波形图和频谱图如图14所示。

图13 脉冲指标随时间变化曲线图Fig.13 Pulse indicator over time curve

图14 AM-FM1时域、频域图Fig.14 AM-FM1 time domain, frequency domain diagram

以第1个分量为例构建Hankel矩阵，画出奇异值分解图15(a)和差分谱15(b)，取前50个点绘制在一起如图15(c)所示。

图15 奇异值差分谱降噪过程Fig.15 Singular value difference spectrum de-noising process

从图15(c)可以看到，最大的峰值发生在第2个点，表明奇异值序列在此位置发生了最大的突变。取前两个分量进行重构，如图16所示。

图16 AM-FM1降噪时域、频谱图Fig.16 Time domain, frequency domain diagram of the AM-FM1 after de-noising

同理可以得到AM-FM2和AM-FM3的降噪时域、频谱图，如图17,18所示。

图17 AM-FM2降噪时域、频谱图Fig.17 Time domain, frequency domain diagram of the AM-FM2 after de-noising

图18 AM-FM3降噪时域、频谱图Fig.18 Time domain, frequency domain diagram of the AM-FM3 after de-noising

为验证降噪方法的有效性，将奇异值差分谱降噪分别与小波阈值降噪、CEEMD强制降噪进行对比，如图19所示。可以看出，奇异值差分谱降噪后的信号更接近原始信号。

图19 降噪效果对比Fig.19 Contrast of de-noising effect

图20 滚动轴承振动测试试验台Fig.20 Rolling bearing vibration test rig

采用3种方法降噪后，分别计算重构后信号与原始信号的相关性，相关性越高，说明降噪方法对信号的还原度越高。MBCV-EWT与奇异值差分谱降噪后信号与原始信号的相关系数为0.936 1；CEEMD的相关系数为0.438 2；小波变换的相关系数为0.488 5。可见，MBCV-EWT与奇异值差分谱相结合的降噪方法明显优于前两种。

3.2 实验验证

本论文主要研究早期故障阶段，采用如图20所示的试验台模拟实验来验证笔者提出的微弱信号检测、信号分解、降噪与特征提取方法的有效性。滚动轴承振动测试试验台主要由SGM7J-04AFC6S伺服电机、YMC122A100加速度传感器、POD-0.6 kg磁粉制动器、GFC-40X66梅花联轴器和底座等连接件与紧固件组成。

该实验用CoCo-80动态信号分析仪采集信号数据，3204ATN双列角接触球轴承，参数如表1所示。根据滚动轴承常见故障位置与故障类型，实验主要模拟外圈裂痕故障。外圈裂痕情况如图21所示，图中圆圈即为裂痕位置，裂痕为电火花线切割的0.31 mm的轻度故障。转速n=1 kr/min，采样频率f=400 Hz，通过计算得到外圈的故障频率约为 52.98 Hz。