基于轴心轨迹形态的转子裂纹故障分析与诊断*

向 玲， 张 悦

(华北电力大学(保定)机械工程系 保定，071003)

引 言

转子系统在运行中转子故障时有发生。由于材料加工的原始缺陷和转子的疲劳运转，使之产生裂纹故障。单一的碰摩故障和裂纹故障均会使系统的振动加剧，对转子的正常运转产生影响。当碰摩和裂纹故障同时存在时，会使系统的非线性行为更加复杂，存在安全隐患。因此，在故障发生之前及时诊断，可极大地减少经济损失及人员伤亡，对工业生产具有重大意义。艾延廷等[1]基于融合信息熵距，提出了一种转子振动故障的诊断方法。文献[2]针对仿真结果和实验转子的故障信号，对转子不平衡、碰摩和油膜涡动故障提出了基于局部均值分解的故障诊断方法。文献[3]提出用自适应经验小波变换的方法诊断转子碰摩故障，克服了希尔伯特变换的瞬时频率。孙斌等[4]基于复杂网络的动力学统计量，对转子系统振动故障作出诊断。

故障转子的非线性动力学研究一向是学者们研究的重点，其中裂纹和碰摩这两种常见故障尤为重要。文献[5-6]基于裂纹-碰摩故障转子系统的动力学模型，利用延拓打靶法研究了系统周期运动的稳定性。刘元峰等[7]运用龙格-库塔法研究了转子在裂纹和碰摩这两种非线性因素作用下的非线性行为。Mohammad[8]利用有限元模型和谐波平衡法，讨论了基于时变刚度的裂纹转子系统的动态稳定性。Hamid等[9]采用改进的谐波平衡法发现第2裂纹的存在对系统临界转速的影响。

学者们还对转子系统的动力学研究进行了实验验证。Guo等[10]对裂纹转子的动力学行为和基于经验模态分解的裂纹检测方法进行了实验验证。Yang等[11]对存在不平衡和定点摩擦的双转子系统的动力学特性进行了理论分析和实验研究。Anuj等[12]从裂纹深度和位置等多方面对多裂纹转子系统的非线性动力学行为进行实验验证和分析。Kumar等[13]通过Ansys设计了简化的实验装置模型，对不同参数的裂纹轴进行了谐波分析。已有的研究多从动力学角度对故障转子进行分析，利用频谱图对故障转子进行诊断，而基于轴心轨迹形态对裂纹故障进行分析的较少。

笔者从轴心轨迹的形态分析角度出发，通过对比分析无故障和裂纹故障转子系统、碰摩故障和碰摩-裂纹双故障转子系统1/2临界转速附近的轴心轨迹形态变化，提供了一种诊断系统裂纹故障的新方法，同时利用分岔图和频谱图分析了不同转子系统的动力学响应。

1 含裂纹-碰摩双故障的转子系统

图1为含裂纹-碰摩双故障的Jeffcott转子模型。转轴两端为对称刚性支承，无裂纹的转轴刚度为k，转轴中间位置安装一圆盘，圆盘的质量为m，圆盘的阻尼为c。一个横向裂纹位于转轴中部靠近圆盘处，圆盘几何中心为O1，圆盘质心为O2。

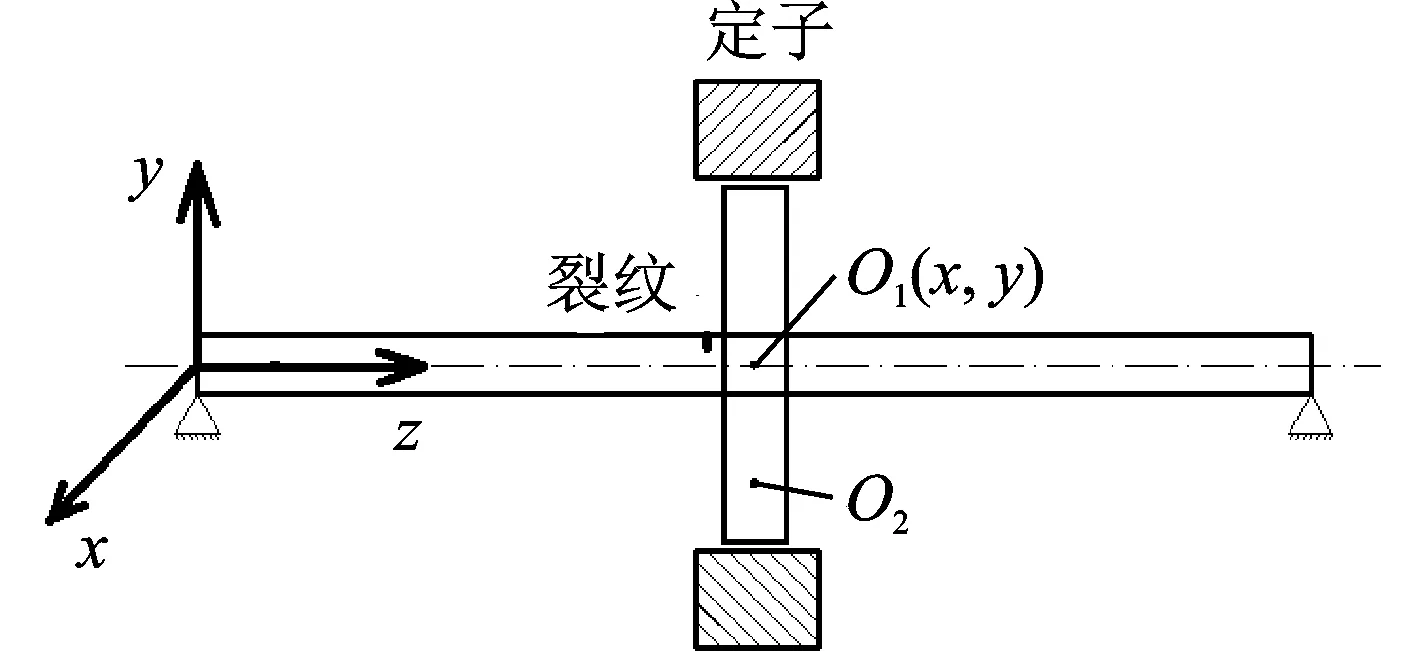
图1 裂纹-碰摩双故障转子系统Fig.1 Rotor system with coupling fault of crack and rub-impact

1.1 碰摩力模型

在碰摩发生的过程中，对碰摩转子进行简化，转、定子之间的碰撞视为弹性碰撞，不计热效应，碰摩视为局部碰摩。碰摩发生时的切向摩擦力为PT，法向碰摩力为PN，e为圆盘的偏心量，碰摩力的求解公式为

(1a)

PT=μPN

(1b)

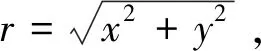
将碰摩产生的切向和法向碰摩力分解到x方向和y方向[8]为

(2)

1.2 裂纹转子开闭模型

图2为转轴的横向裂纹截面示意图。xOy和ξO′η分别为系统的固定坐标系和转动坐标系，转轴的中心为O′，转动坐标系中的O′ξ轴与裂纹扩展方向一致，转子在旋转过程中仅考虑弯曲振动。本研究的裂纹模型采用开闭裂纹模型，其张开与闭合程度随着重力和不平衡力合力的周期变化而变化。图中：θ=ωt+φ0；φ0为转轴初始相位角，这里设定φ0=0；α为一半的裂纹角；ψ为转轴的涡动角，ψ=arctan(y/x)；β为偏心量和裂纹方向之间的夹角，设β=0；φ为转涡差角，φ=θ+β-ψ。

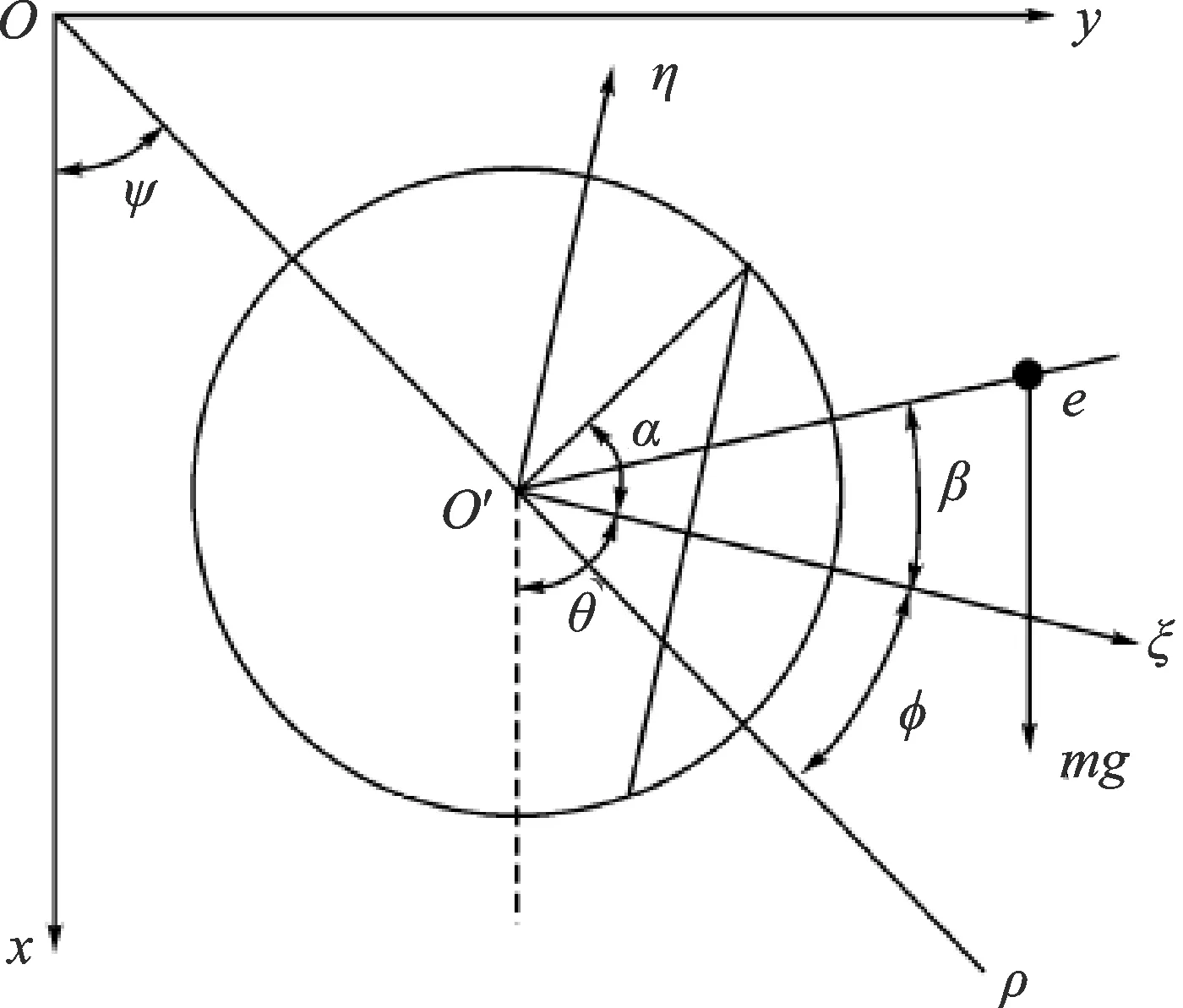
图2 裂纹截面示意图Fig.2 Schematic diagram of cross section of transverse crack

在笔者研究的裂纹-碰摩双故障转子模型中，考虑到不同裂纹深度对转轴刚度的影响，选用的裂纹开闭模型为将裂纹深度考虑在内的非线性模型

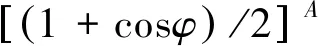
(3)

其中：A=a/R，为转轴的无量纲裂纹深度；a为裂纹深度；R为转轴半径。

1.3 裂纹刚度模型

笔者建立的裂纹-碰摩双故障转子模型中，转轴的两端为刚性对称支承，忽略系统的耦合刚度。在转轴转动的过程中，裂纹的存在会时刻改变横截面所受的应力大小及方向，矩阵K为变化后的刚度矩阵。在转轴刚度变化的过程中，忽略O′η轴方向的变化，即ΔK=ΔKξ，故变化后的刚度矩阵表达式[8]为

(4)

其中：f(φ)为呼吸裂纹的开闭函数；k为转轴刚度；Δk为有裂纹的转轴刚度变化量。

将计算中所用的转动坐标系ξO′η替换为固定坐标系xOy，则式(4)中的各刚度可表示为

kxx=k-f(φ)Δkcos2(φ+ψ)

(5)

kxy=kyx=-f(φ)Δkcos(φ+ψ)sin(φ+ψ)

(6)

kyy=k-f(φ)Δksin2(φ+ψ)

(7)

2 裂纹-碰摩转子系统运动微分方程

2.1 裂纹-碰摩转子系统运动微分方程的建立

假设x和y分别为转轴中央圆盘处的径向位移，不考虑陀螺力矩和扭转振动。根据Lagrange方程将两端支承连线的中心视为零势能点，得到裂纹-碰摩双故障转子系统的运动微分方程为

(8)

其中：m为圆盘质量；c为圆盘阻尼系数；k为无裂纹的转轴刚度；e为圆盘偏心量；ω为转轴转速；Px为系统x方向的碰摩力；Py为系统y方向的碰摩力。

2.2 裂纹-碰摩转子系统运动微分方程的求解

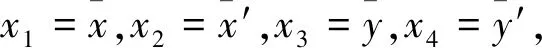
(9)

(10)

3 数值仿真与分析

转子系统中的故障存在会使系统响应发生不同程度变化。转子中裂纹故障会对转轴刚度产生一定影响，进而使系统响应发生一系列变化。根据裂纹故障对系统响应引发的规律变化，可对系统的裂纹故障进行初步诊断。

3.1 无故障及裂纹故障转子系统的仿真与分析

利用四阶龙格-库塔法对无量纲化后的非线性方程组进行求解，无故障转子系统和裂纹转子系统的参数设定如表1所示。另外，无故障转子系统的无量纲裂纹深度A=0，裂纹转子系统中的设定为A=0.3。考虑到瞬态响应的影响，故选用100周期以后的计算结果进行仿真，得到系统的分岔图和1/2临界转速附近的轴心轨迹图，如图3，4所示。

表1 无裂纹及裂纹故障转子系统参数

Tab.1 System parameters of the uncracked rotor and the cracked rotor

参数符号数值圆盘质量/kgm0.594 3圆盘阻尼/(N s·m-1)c10.89定子刚度kc0转子刚度/(N·m-1)k19 959偏心量/mme0.085转轴半径/mmR5

由图3可知，在转速为0～1.5倍临界转速区间内，无故障Jeffcott转子系统和裂纹故障转子系统均未出现分岔，始终为单周期运动。由图3(a)可知，无故障转子系统运动较为稳定。在图3(b)中，曲线存在多处峰值，即当系统转速比为1/n(n=1,2,…)时,系统出现共振现象。对比图3 (a), (b)，虽然两图具有不同特征，但不能为裂纹故障的诊断提供有力条件。

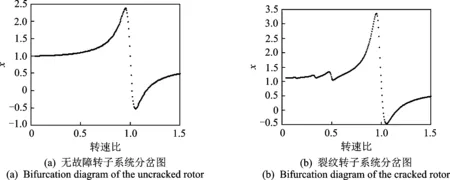
图3 无故障转子系统和裂纹转子系统分岔图Fig.3 Bifurcation diagram of the uncracked rotor and the cracked rotor

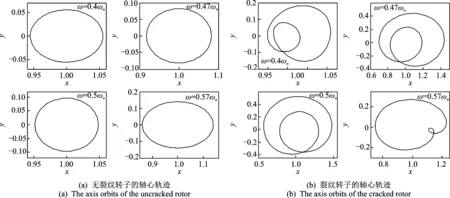
图4 1/2临界转速区无裂纹转子和裂纹转子的轴心轨迹Fig.4 The axis orbits of the uncracked rotor and the cracked rotor around the 1/2 subcritical speed zone

从图4(a)可以看出，在1/2临界转速附近，无故障转子系统的轴心轨迹均为光滑圆环，随着转速变化，仅仅是圆环大小发生变化，并没有内环出现。在图4(b)中，裂纹转子系统的轴心轨迹在转速变化区间内始终存在一个内环，且内环的形状和偏置角度均随转速的变化而变化，其中内环的偏置方向在转速区间内的旋转角度约为π。

对比有无故障转子的轴心轨迹可知，通过判断系统1/2临界转速附近的轴心轨迹有无内环出现，且偏置角度是否为π，可以为系统中裂纹故障的诊断提供一种简便方法。

3.2 碰摩故障及裂纹-碰摩转子系统的仿真与分析

碰摩转子系统和裂纹-碰摩转子系统的参数设定如表2所示。碰摩转子系统的无量纲裂纹深度A=0，在裂纹-碰摩转子系统中设定A=0.3。同样考虑瞬态响应的影响，选用100周期以后的计算结果进行仿真，对转子系统响应进行对比分析。

表2 碰摩转子和裂纹-碰摩转子系统参数

Tab.2 System parameters of the rub-impact rotor and the crack and rub-impact rotor

参数名称符号数值圆盘质量/kgm0.594 3圆盘阻尼/(Ns·m-1)c41.64摩擦因数μ0.2定子刚度/(105N·m-1)kc1.035 7转子刚度/(105N·m-1)k1.726 2偏心量/10-3mme9.8转轴半径/mmR5

由图5 (a)可知，在转速为0～1.5倍临界转速区间内，碰摩转子系统未出现分岔，始终为单周期运动。图5(b)为裂纹-碰摩转子系统的分岔图，可知系统发生三分岔的转速为0.492倍的临界转速，在此之前系统为单周期运动。系统经过短暂的三周期运动后，在转速为0.495倍的临界转速处进入二周期运动, 继而系统又在转速为0.498倍的临界转速处经过倒分岔回归到单周期运动。

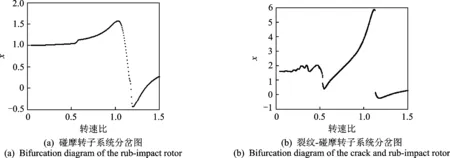
图5 碰摩转子系统和裂纹-碰摩转子系统分岔图Fig.5 Bifurcation diagram of the rub-impact rotor and the crack and rub-impact rotor

图6 碰摩转子系统和裂纹-碰摩转子系统1/2临界转速区的轴心轨迹Fig.6 The axis orbits of the rub-impact rotor and the crack and rub-impact rotor around the 1/2 subcritical speed zone

图6为碰摩转子系统和裂纹-碰摩转子系统1/2临界转速附近的轴心轨迹图。由图6(a)可知，碰摩转子系统在1/2临界转速附近，轴心轨迹图中无明显的内环出现，圆环存在轻微凹凸现象，这是由于系统的碰摩故障所致。由图6(b)可以看出，裂纹-碰摩转子系统1/2临界转速附近的轴心轨迹形态呈现出规律变化。图中的轴心轨迹始终存在一个内环，且随着转速升高，内环的形状和偏置方向均发生变化。在转速变化范围内，内环逐渐变小，其偏置方向也旋转一定角度。与裂纹故障转子系统的轴心轨迹相对比，此时由于碰摩故障的存在，使轴心轨迹内环的旋转角度有一定的减小，略小于180°。

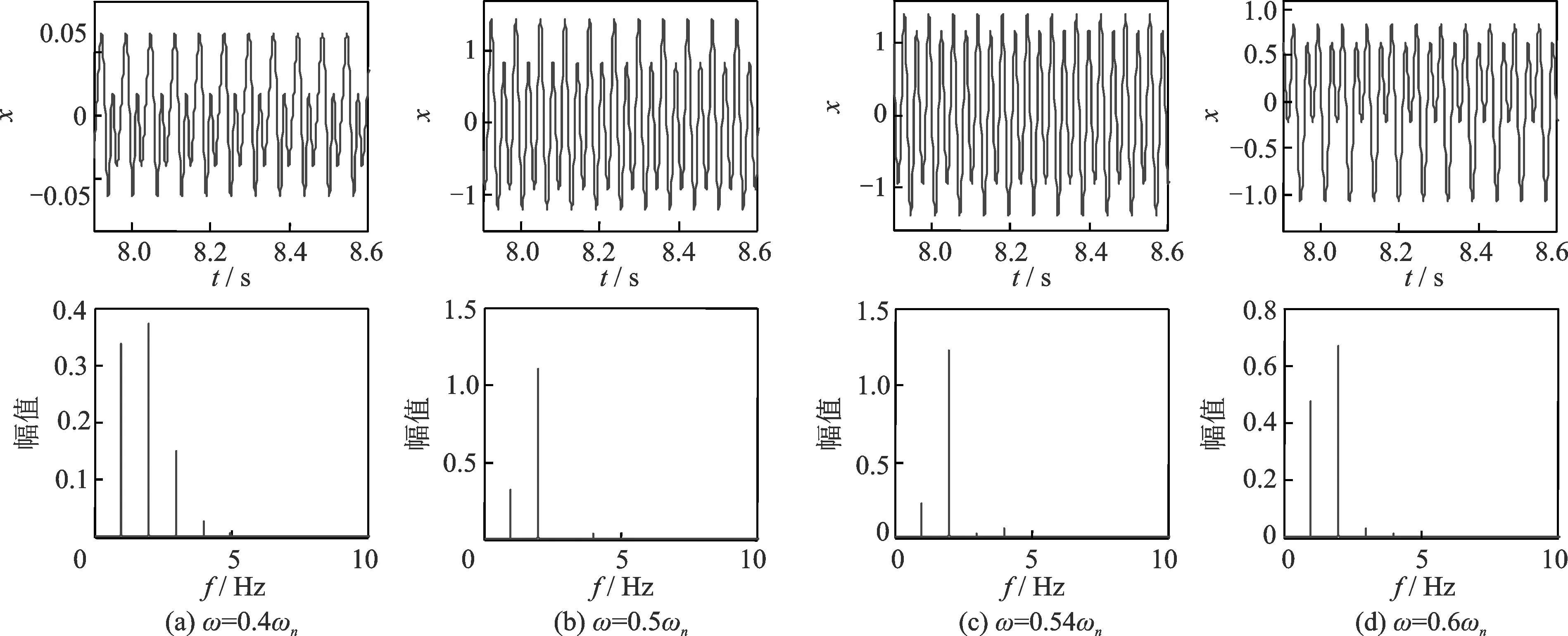
图7 裂纹-碰摩转子系统1/2临界转速区的时域波形图和频谱图Fig.7 Time series and frequency spectra of the crack and rub-impact rotor around the 1/2 subcritical speed zone

因此，在裂纹-碰摩双故障转子系统中，通过观察系统1/2临界转速附近的轴心轨迹图是否存在内环、内环的偏置方向是否在转速变化范围内旋转一定角度，便可对转子系统的裂纹故障作出初步诊断。

图7为裂纹-碰摩转子系统对应转速下的时域波形图和频谱图。可以发现，系统波形均为周期信号，并有“削波”现象存在。在频谱图中随着转速变化，各谐波分量幅值有所变化，由于裂纹故障的存在，其中2X分量明显，另外还存在3X，4X等谐波频率成分，系统碰摩特征也较为明显。

由以上仿真结果可以看出，通过对比无故障Jeffcott转子系统和Jeffcott裂纹转子系统1/2临界转速附近的轴心轨迹图，根据轴心轨迹图中是否存在内环，且内环的偏置角度是否旋转180°，为转子系统中裂纹故障的初步诊断提供一种简便清晰的方法。同样，通过对比Jeffcott碰摩转子系统和裂纹-碰摩双故障转子系统1/2临界转速附近的轴心轨迹图，也可根据图中是否存在内环以及内环是否旋转一定角度，对裂纹-碰摩双故障转子系统中的裂纹故障作出初步诊断。

4 实验研究

对刚性支承下裂纹转子系统进行实验研究，图8为Bently RK-4转子实验台。实验采用5只传感器进行数据测量，分别在两端支承处安装一对呈45°分布测量振动信号，在电机输出端安装一只光电传感器向转速调节器提供反馈信号。实验中ZonicBook/618E振动测试系统用于数据采集，实验台运行稳定，可实现0～10kr/min范围内的无级调速。

此次实验将模拟转子的裂纹故障，图9为裂纹轴的细节图。实验使用一根裂纹深度a=2mm的转轴，该模拟裂纹是利用线切割加工而成。转子系统的临界转速约为2 800r/min，为了对理论仿真进行验证，在实验台完成了定速实验，通过测得振动信号得到转轴相应的轴心轨迹并进行分析。

图8 Bently RK-4转子实验台Fig.8 Bently RK-4 rotor test rig

图9 裂纹轴细节图Fig.9 Schematic diagram of crack shaft

图10为2mm裂纹转子系统1/2临界转速附近的轴心轨迹的实验结果。通过图中箭头的标识可以发现，系统1/2临界转速附近的轴心轨迹存在一个随着转速升高而旋转的内环，且在转速变化范围内其旋转角度接近180°。该实验结果对之前的理论仿真进行了部分验证，证明了通过轴心轨迹特征初步诊断裂纹故障的有效性。另外，此次实验过程中，实验转轴可能存在轻微的不对中，使部分轴心轨迹图中存在一个尖端，在后续的实验中将对该问题进行改进。

图10 实验转轴1/2临界转速区的轴心轨迹Fig.10 The axis orbits of the test shaft around the 1/2 subcritical speed zone

5 结束语

基于转子系统轴心轨迹的形态分析，通过对比无故障转子系统和裂纹转子系统、碰摩转子系统和碰摩-裂纹双故障转子系统1/2临界转速附近的轴心轨迹形态变化，为多故障转子系统中的裂纹故障的初步诊断提供了一种简便的新方法。结果表明：在裂纹-碰摩转子系统中，随着转速升高，系统1/2临界转速附近的轴心轨迹形态呈现出规律和典型的变化。在速度变化区间内，系统轴心轨迹始终存在一个内环，且内环形状和位置均随转速变化而发生变化，其中内环的位置在转速变化区间内的旋转角度接近π。在碰摩转子系统中，其1/2临界转速附近的轴心轨迹并未存在内环，因此可根据系统1/2临界转速附近的轴心轨迹是否存在内环、内环是否旋转一定角度，来判断系统中是否存在裂纹故障，为裂纹-碰摩双故障转子系统中裂纹故障的初步诊断提供了一种新方法。可以看出，该方法与通过对比无故障转子和裂纹转子系统的轴心轨迹来初步诊断裂纹故障的方法类似。笔者通过分岔图、时域波形图及频谱图，对不同转子系统的系统响应进行了分析。可以看出，裂纹-碰摩转子系统的时域波形图呈周期变化，并有“削波”现象存在。系统频谱中包含丰富的谐波成分，碰摩现象明显。在Bently转子实验台对裂纹转子的轴心轨迹进行了实验验证。结果显示，1/2临界转速附近的轴心轨迹存在一个随着转速升高而旋转的内环，且在转速变化范围内其旋转角度接近180°，进一步证明了通过轴心轨迹特征初步诊断裂纹故障的有效性。