行星齿轮箱齿根应变的光纤光栅测量方法*

牛 杭， 侯成刚， 张小栋,2, 赵欣丹

(1. 西安交通大学机械工程学院 西安，710049) (2. 西安交通大学现代设计及转子轴承系统教育部重点实验室 西安，710049)

引 言

行星齿轮箱在航空、能源和运输等领域应用广泛，但在恶劣的运行环境下，其关键部件的故障发生几率很高。目前，振动分析法为行星齿轮箱故障诊断的主要方法，但由于行星齿轮箱内多组振动信号之间的相互耦合、干扰以及变速变载的非平稳性工况的影响，该方法在识别轮齿裂纹等微弱故障时，效果尚不理想。本课题组经分析发现，内齿圈齿根应变与行星齿轮箱啮合力信息之间的映射关系更直接，能更清晰地反应齿轮箱的运行状态。在此基础上，研究了行星齿轮箱故障下的内齿圈齿根应变动态变化机理[1]。然而，为了开展基于内齿圈齿根应变信号的行星齿轮箱监测诊断方法的研究，准确获取齿根应变信号是关键。

传统的齿轮应力/应变测量方法主要有光弹法和电测法。光弹法利用光弹性材料在偏振光场中形成的应力光图分析应力的分布。电测法利用电阻应变片测量特定位置的应变。Wang[2]分析了在不同啮合位置和不同工况参数下，齿根弯曲应力的分布特点。文献[3-5]利用应力密度因数计算了含裂纹轮齿的啮合刚度。Spitas等[6]验证了其提出的无量纲轮齿模型的准确性。 Patil等[7]研究了螺旋角对斜齿轮接触应力的影响。Ligata等[8]分析了制造误差对行星齿轮箱偏载特性的影响。Dai等[9]分析了轮齿修形和接触损失对齿根应变的影响。周辉俊[10]提出了拟合修正系数，为面齿轮的设计和弯曲强度校核提供了有效依据。

光弹法和电测法是两种有效的实验方法，但其并不适合实际行星齿轮箱中齿根应变的监测任务。光弹法需要复杂的光学系统、开放的齿轮啮合环境以及特殊的材料，工业现场很难满足这些条件。相比之下，电测法所需的测试系统较简单，但实际的行星齿轮箱难以为电阻应变片提供足够的安装空间，研究人员大部分将这种方法用在定轴齿轮箱中。文献[8]利用电阻应变片测量了内齿圈齿根应变，但使用的是专门用于实验的行星齿轮箱，其内部空间较为宽裕，对于分布式应变测量，安装空间问题更为突出。另外，电测法不具备抗电磁场干扰的能力。

FBG已经成功应用于多种结构的应变监测中[11-12]。由于光纤光栅具有体积小、适合于分布式监测及抗电磁干扰等优势，本课题组提出利用光纤光栅对行星齿轮箱内齿圈齿根应变进行在线测量[13]，然而对于内齿圈这一特殊结构，关键测量问题还需要深入分析。

笔者在课题组前期工作的基础上[14-15]，提出了一种行星齿轮箱内齿圈齿根应变的光纤光栅动态测量方法。首先，对行星齿轮箱内齿圈齿根应变的动态变化规律进行理论计算分析；其次，从测试原理、测点布置及测量系统构建等角度对提出的光纤光栅动态测量方法进行深入研究；最后，开展了内齿圈齿根应变光纤光栅动态测量实验，并将实验结果与仿真结果进行对比分析，对所提出方法的有效性进行评价。

1 内齿圈齿根应变分析

1.1 内齿圈齿根应变计算方法

本研究对象为单级行星齿轮箱，内齿圈固定。在平衡状态下，行星轮与内齿圈之间的啮合力为

(1)

其中：TD为对太阳轮施加的转矩；N为齿轮箱中行星轮的个数；Rsb为太阳轮的基圆半径。

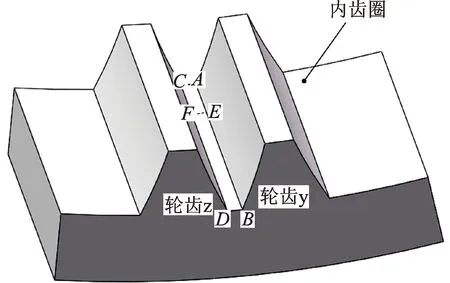
图1 内齿圈简化模型Fig.1 Simplified model of the ring gear

式(1)中，Frp体现了单个行星轮对内齿圈的整体作用，但由于齿轮啮合过程中存在单、双齿交替啮合现象，所以对于内齿圈的某一个轮齿，其在啮合过程中所受到的力并不恒定为Frp。当只有一对轮齿啮合时，Frp由该对轮齿完全承担；当两对轮齿参与啮合时，Frp由这两对轮齿共同承担。Frp在这两对轮齿上的分配原则在不考虑工况参数变化的情况下，文献[16]从能量上进行了阐述，只考虑了弯曲变形能。实际上啮合刚度就是对轮齿弯曲、压缩、剪切及接触等变形能的一个综合反映，所以笔者认为啮合过程中齿间载荷的分配取决于两对轮齿啮合刚度的相对大小更加直观。例如，当行星轮上相邻的两个轮齿m，n分别与图1所示内齿圈上相邻的两个轮齿y，z发生啮合时，内齿圈轮齿所受啮合力可分别表示为

(2)

(3)

其中：kmy为轮齿m，y的啮合刚度；knz为轮齿n，z的啮合刚度。

笔者采用文献[17]中的有限元方法计算啮合刚度。内齿圈齿根应变利用有限元方法计算。首先，在Solid Works中建立如图1所示实体模型，并将其导入Ansys；其次，对Ansys中的模型进行网格划分，约束内齿圈外表面所有方向自由度；然后，将Frp,y和Frp,z分别作为线载荷加载到轮齿y和轮齿z的特定部位(在啮合过程中的某一时刻，Frp,y和Frp,z具有确定的数值和加载位置)，加载线与AB线平行；最后，进行静力学求解(不考虑冲击和工况参数变化对齿根应变的影响)。通过以上过程，可以在Ansys后处理器中提取啮合过程中某一时刻内齿圈齿根应变的数值。

1.2 内齿圈齿根应变仿真计算

仿真计算内齿圈齿根应变时用到的行星齿轮箱与后续实验中的一致，其参数如表1所示。

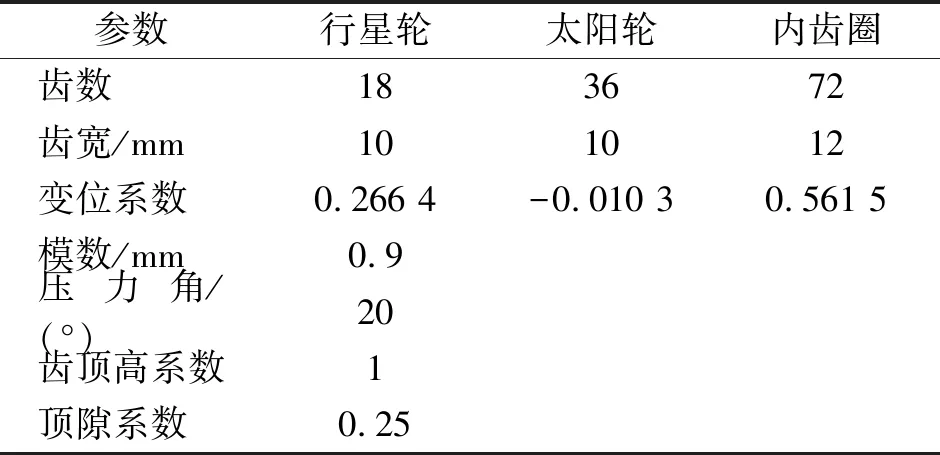
表1 行星齿轮箱参数Tab.1 Parameters of the planetary gearbox

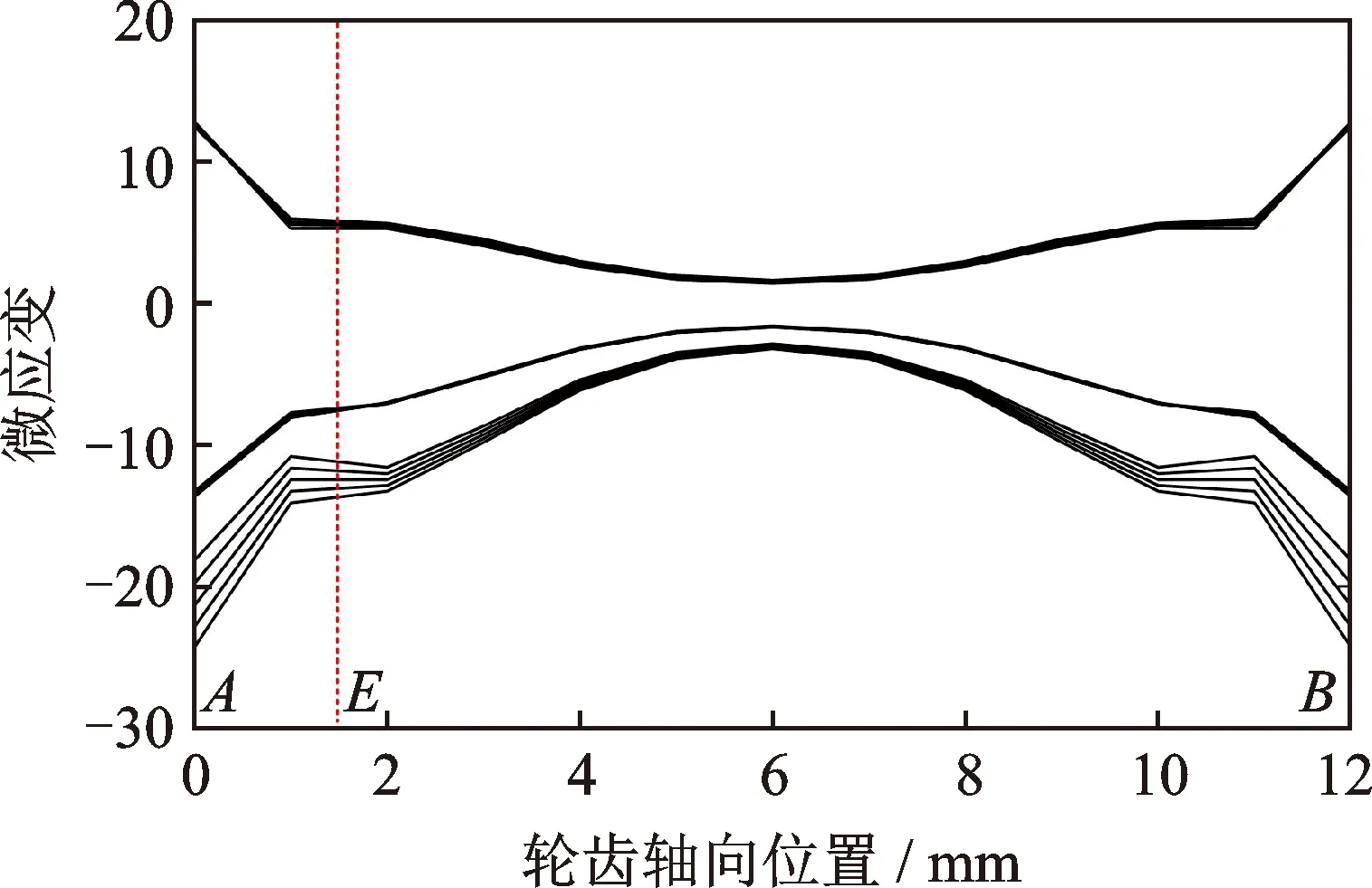
图2 内齿圈齿根应变分布曲线Fig.2 Distribution of the tooth root strain of the ring gear

在轮齿y从进入啮合到退出啮合的过程中，按照时间先后顺序选取了14个离散的时间点。图2为在这14个时间点加载时(负载转矩为30Nm)，内齿圈齿根AB线上的轴向应变分布曲线(纵坐标微应变为无量纲参数)，该组曲线从下到上与14个时间点对应。可以看出，内齿圈齿根应变在轴向呈现非均匀分布的特点，且靠近轮齿边缘部位的应变绝对值大，中间应变绝对值小。

图3为在11.4，19.2和30Nm的负载转矩下，AE区域(AE长度为1.5mm)的平均轴向应变随啮合过程的变化曲线。为了便于分析比较，将图3(以及后续应变曲线图)中的横坐标以啮合周期为基准做归一化处理。可以看出，AE区域的平均应变呈现出明显的单、双齿交替啮合区间。

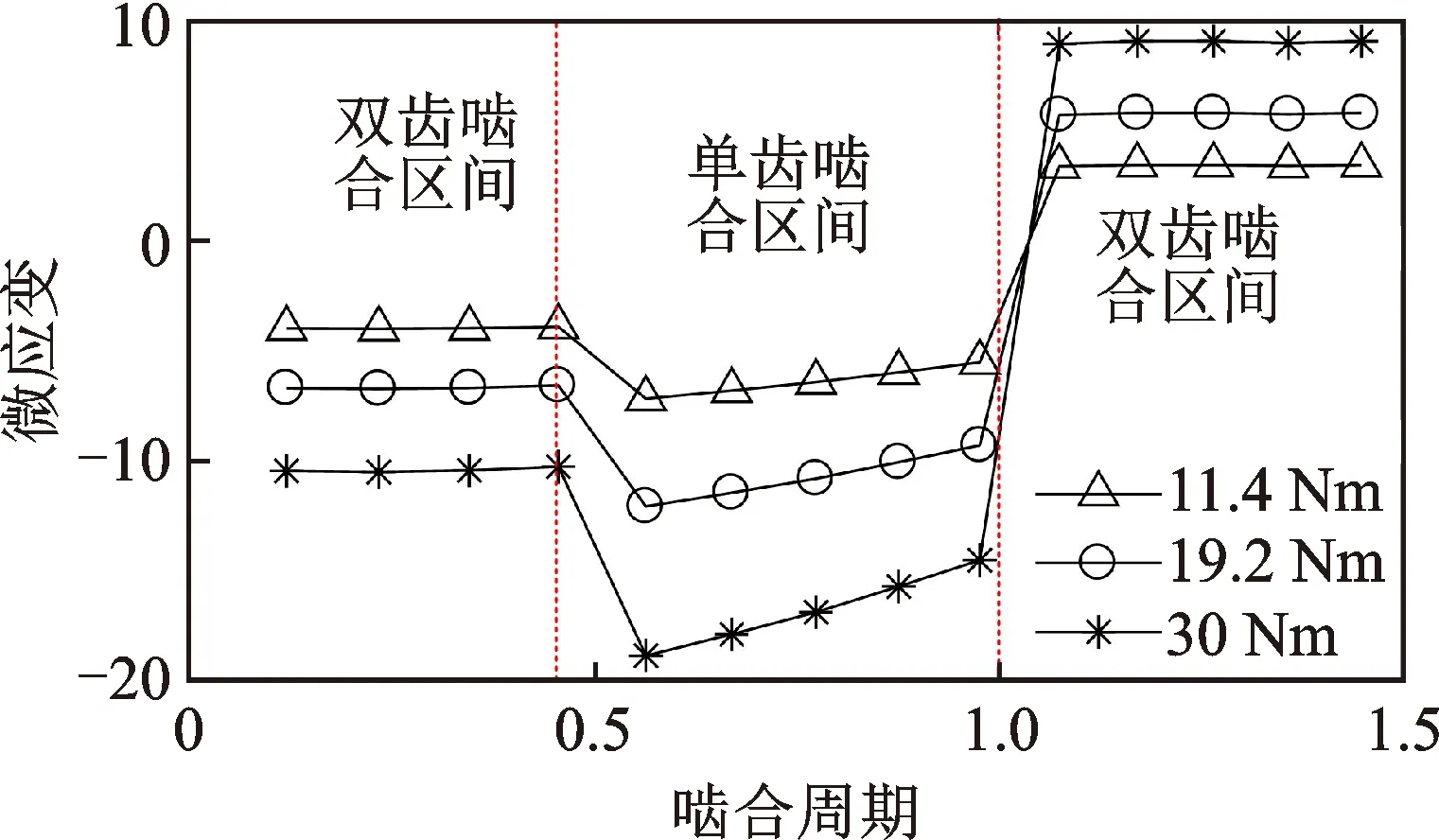
图3 内齿圈齿根应变在啮合过程中的变化曲线Fig.3 Tooth root strain of the ring gear during the meshing process

2 内齿圈齿根应变光纤光栅测量方法

2.1 测量原理

光纤由纤芯和包层组成，光纤光栅是在纤芯中通过紫外光照射等手段加工而成的结构，该结构对特定波长的光具有反射作用，反射光的谐振波长与光纤光栅的周期和纤芯有效折射率有关。

光纤光栅的轴向变形会使其反射波长产生偏移，轴向应变量ε与波长偏移量Δλ的关系为

(4)

其中：λB为光纤光栅未发生变形时的反射光谐振波长；pe为有效弹光系数，该值为常数。

若将裸光纤光栅(外部无封装结构)直接粘贴在被测区域，并且忽略胶结剂对应变灵敏度的影响，则由式(4)可知，只要获得光纤光栅变形前后的谐振波长偏移量，即可计算得到被测区域的应变。但式(4)严格来讲是均匀应变场作用下的光纤光栅应变传感模型，内齿圈齿根应变在轴向呈现非均匀分布的特点，所以利用式(4)计算内齿圈齿根应变的合理性需要讨论。本研究所用方法为：计算在内齿圈齿根非均匀应变作用下光纤光栅的反射率，从反射光谱中提取光纤光栅的谐振波长值，并计算波长偏移量，通过式(4)计算应变，并比较该应变与测试区域平均应变的差异。

计算非均匀应变作用下光纤光栅的反射率采用传输矩阵法[18]。将光纤光栅分成长度相等的M段，假设每段光纤光栅范围内的应变均匀分布，则光纤光栅内的电场幅度可以表示为

(5)

Tk为第k段光栅的传输矩阵

(6)

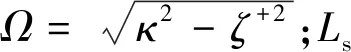
根据式(5)和式(6)，光纤光栅的反射率为

(7)

非均匀应变场影响式(6)中的直流耦合系数，如式(8)所示

(8)

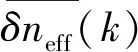
如果光纤光栅沿齿轮轴向粘贴在图1中的AE区域，则行星齿轮箱在11.4，19.2和30Nm的负载转矩下，光纤光栅谐振波长偏移量及由其计算的应变随啮合过程的变化曲线如图4所示。

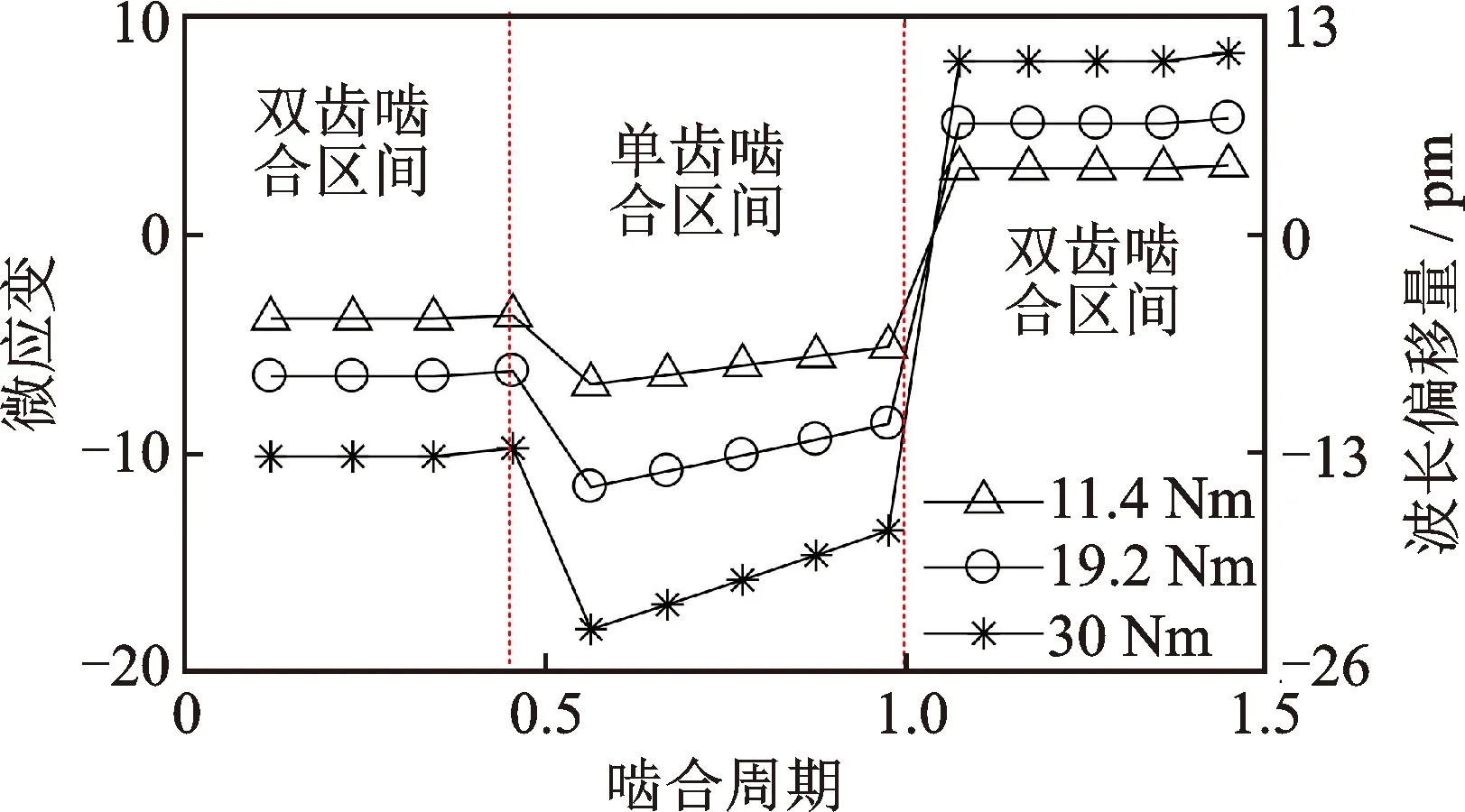
图4 光纤光栅谐振波长偏移量及由其计算得到的内齿圈齿根应变Fig.4 Wavelength change of FBG and the calculated tooth root strain of the ring gear

对比图3, 4可以看出，在内齿圈齿根部位非均匀应变场作用下，利用光纤光栅谐振波长偏移量计算的应变与测试区域的平均应变虽不完全相等，但两者所呈现出的啮合区间范围是一致的，且在啮合周期的同一位置，两者的数值非常接近。另外，考虑到测试内齿圈齿根应变的最终目的在于故障诊断，所以关注的应该是应变的相对变化量，而不是应变的绝对大小。因此，利用光纤光栅谐振波长的偏移量并通过式(4)计算的应变可以足够准确地反映测试区域的平均应变，并作为齿轮箱的故障特征载体信号。

2.2 光纤光栅传感单元的布置与设计

因为光纤光栅直径较小，在内齿圈的顶隙部位具有一定的安装空间，所以理论上光纤光栅在齿根处可以与齿轮轴向成一定角度倾斜粘贴，如图5所示。本课题组前期建立了所测应变与安装角度的关系模型，并进行了实验验证[15]，发现在AB线的同一位置处，只有当安装角度θ为0时，才能使光纤光栅测量到的应变绝对值最大，所以笔者将光纤光栅与齿轮轴向平行粘贴在图1中AB线上。需要指出的是，此时获得的应变(即AB方向应变)性质与图5中r方向(与AB垂直且与齿面相切)的应变性质不同。例如，当r方向为拉应变时，光纤光栅测得的应变为压应变。

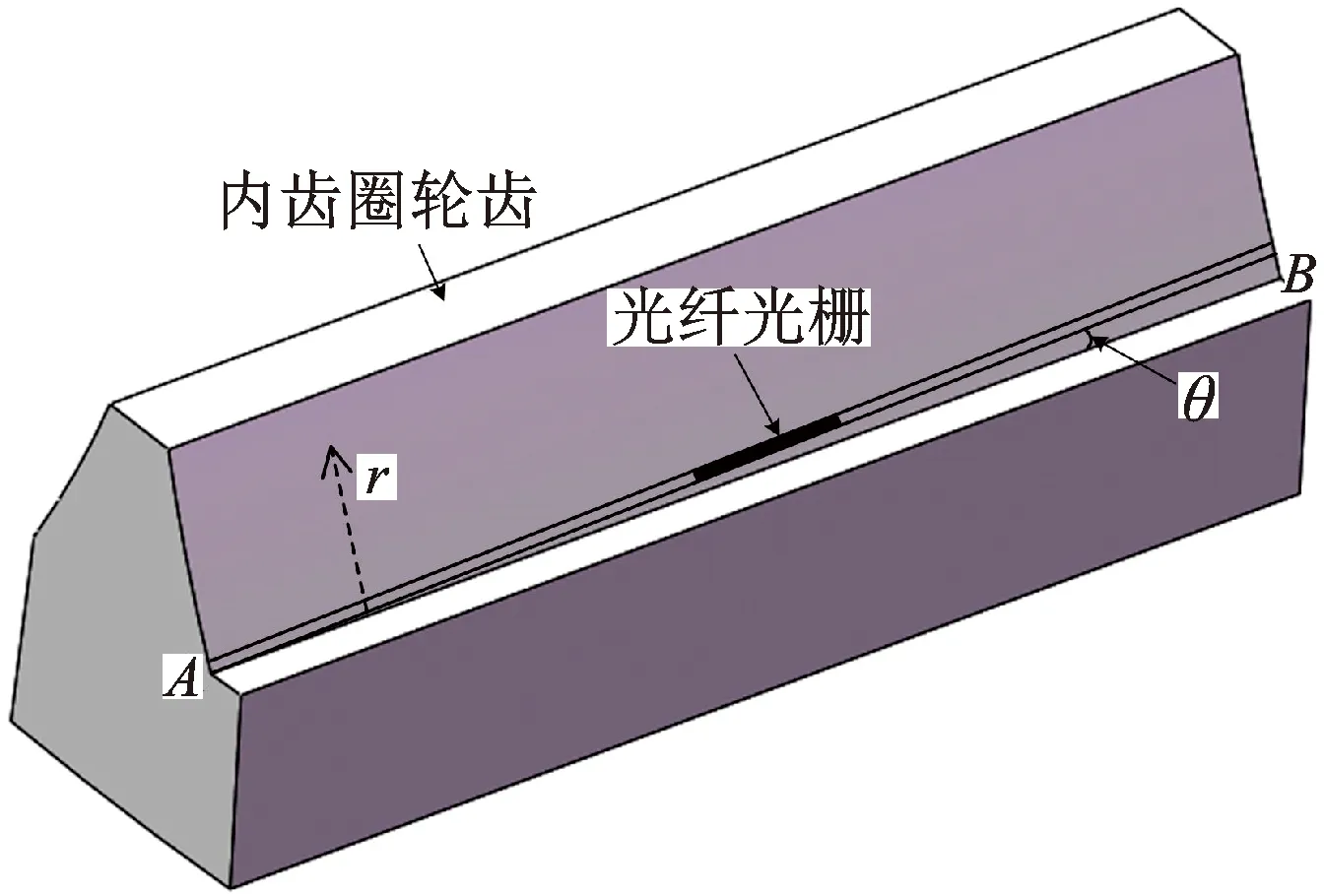
图5 光纤光栅倾斜粘贴示意图Fig.5 Slant installation of FBG

在明确了粘贴方向后，光纤光栅的长度及其在AB上的位置是两个需要考虑的问题。理论上，在其他参数一定的情况下，光纤光栅越长，其反射率越大，反射谱的带宽越小，谐振波长的检测精度越高；光纤光栅越短，其反射率越低，反射谱的带宽越大，谐振波长的检测精度越低。因此，光纤光栅越长，检测到的应变越准确。但是从故障诊断的角度考虑，检测到的应变信号应尽可能大，否则其信噪比将偏低。由测量原理可知，最终检测到的应变反映的是光纤光栅测试范围内的平均应变，为了获取更大应变，应该使光纤光栅的长度尽可能小，并靠近齿轮端面粘贴。综上所述，确定光纤光栅的长度及其粘贴位置，应全面考虑测试对象的尺寸、应变的检测精度以及信噪比。针对本研究的测试对象(如表1所示)，设计的光纤光栅长度为1.5mm，并粘贴在图1中的AE位置。

图6为利用传输矩阵法计算的该光纤光栅初始反射光谱，纵坐标反射率为无量纲参数，其最大反射率为0.28，3dB带宽为0.78nm，边模抑制比为17dB。光纤光栅其他主要参数：纤芯有效折射率为1.48；光栅周期为0.52μm；交流折射率变化最大值为3×10-4。

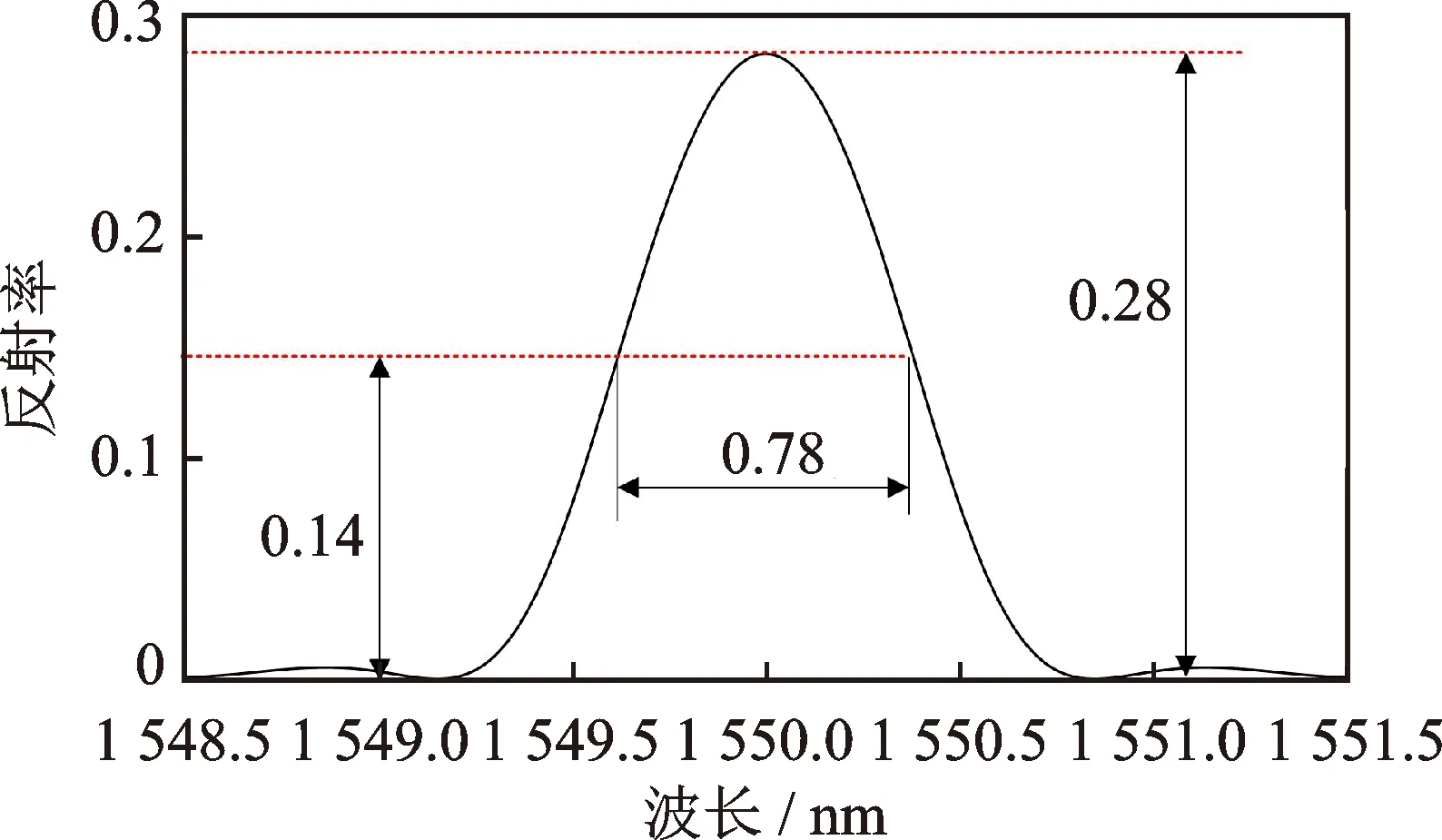
图6 光纤光栅反射光谱Fig.6 Reflected spectrum of FBG

2.3 后续测量系统的构建

由以上分析可知，内齿圈齿根应变测量的关键在于准确获取光纤光栅反射光的谐振波长值。虽然检测光纤光栅谐振波长的方法很多，但由于行星齿轮箱啮合频率较高，所以要保证波长解调速度足够快，才能不失真采集齿根应变。目前，能够在工程上应用并满足上述要求的后续测量系统构建方案如图7所示。波长解调仪选用的是国际上领先的MOI公司产品SM130，该仪器的波长解调频率能够达到1kHz，但价格较高，解调仪分为硬件部分及与之配套的上位机软件。图7所示系统的原理为：扫描光源在每个扫描周期内均发出同样的一组波长随时间变化的窄带光信号；光源发出的光经过光耦合器后分为两部分，一部分进入光纤光栅，另一部分进入梳状滤波器(只允许特定几种波长的光通过)。由于两种光学器件对光波长的选择作用，光纤光栅的反射光和梳状滤波器的透射光经过光电转换和信号处理后，在时域上会呈现出各自的光谱形态。对于梳状滤波器的透射光谱，每一个波峰位置对应的波长值已知，可以根据已知的波长信息通过分段线性插值等方法对光纤光栅反射光的谐振波长值进行实时标定，该过程在波长解调运算模块中实现。光纤光栅的反射光谐振波长信息进入上位机，上位机中的波长解调仪软件能够显示光纤光栅反射光谱波形，并在线实时记录其谐振波长值。由于SM130为通用仪器，软件难以进行二次开发，所以齿根应变计算以及数据分析处理的工作需要放在Matlab软件中离线进行。

图7 内齿圈齿根应变光纤光栅测量系统原理图Fig.7 Measurement system of the tooth root strain

3 内齿圈齿根应变测量实验与分析

为了验证笔者所提方法的有效性，搭建了一个行星齿轮箱实验台，利用图7所示的系统对内齿圈齿根应变进行动态测量，如图8所示。其中，三相异步电机为行星齿轮箱提供输入转速和驱动转矩，磁粉制动器为行星齿轮箱提供负载转矩。由于裸光纤在图中较难识别，所以用白色虚线表示了光纤的路径。

图9为本实验中所使用的光纤光栅探头，光纤光栅传感单元位于去除涂覆层后的光纤区域，长度为1.5mm，直径为0.125mm，实验中所用齿轮箱的内齿圈的顶隙约为0.3mm，所以粘贴的光纤光栅探头不会影响齿轮啮合。

在内齿圈齿根处粘贴光纤光栅如图10所示。光纤从行星架轴所在的端盖上打孔引出，如图11所示。

图8 内齿圈齿根应变测量现场图Fig.8 Measurement experiment of the tooth root strain

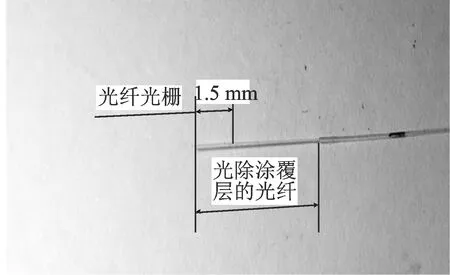
图9 光纤光栅探头结构Fig.9 Structure of the FBG probe

图10 光纤光栅布置现场图Fig.10 Installation of FBG in the experiment

图11 光纤的引出方式Fig.11 Extraction of the fiber from the gearbox

实验时，通过自主开发的上位机软件控制电机的转速和磁粉制动器施加的负载，实时读取转速和负载信息。本实验期望获得在相同的输入转速(100r/min)和不同负载(11.4，19.2和30Nm)下，齿根应变动态变化曲线，但由于实验台的开环控制系统结构以及三相异步电机的负载特性，所以当负载变化后，电机的转速也会变化。为了维持电机转速不变，每次改变负载时，需要根据读取的转速数据对电机转速进行调整。按照以上方法，从测量到的应变数据中截取内齿圈检测齿从进入到退出啮合过程中的应变曲线，如图12所示。可以看出，内齿圈齿根应变基本上随着负载转矩的增加而等比例增加。

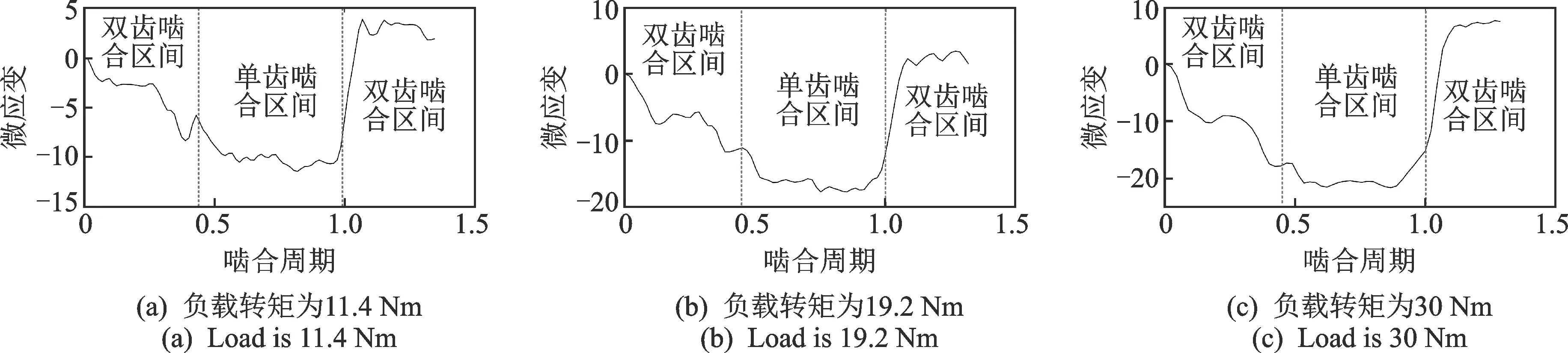
图12 不同负载下，内齿圈齿根应变曲线Fig.12 Ring gear tooth root strain at different loads

对比图12，3和图4可以看出，实验和理论计算得到的齿根应变曲线在单、双齿啮合区间的范围上基本一致，且在每个区间范围内，齿根应变数值近似相等。但是实验和理论曲线仍存在一些区别，出现的差异及其原因如下。

1) 在相同啮合区间内，齿根应变数值并不完全相等。出现这种现象的原因为：a.从测试精度上考虑，测试仪器(SM130)会引入约为2 με的测量误差；b.测试过程中负载转矩并不完全恒定，还存在波动；c.通过对测试时间段内的转矩信号进行分析发现，实验中的行星齿轮箱具有一定程度的偏载现象(工业现场中这种现象也较常见)，这意味着不同部位的内齿圈轮齿所受的啮合力并不完全相同，而理论计算是在理想的情况下进行的；d.由于实验直接测量的是光纤光栅反射波长值，再根据式(1)换算成齿根应变，应变灵敏度使用的是理论值(对于设计反射波长为1 550nm的锗硅光纤光栅，该值为1.3 pm/με)，实际上，由于光纤光栅是利用胶黏剂粘贴在内齿圈齿根部位，所以胶黏剂的种类、胶结层的厚度、胶结宽度和长度等因素均会对光纤光栅的应变灵敏度产生影响。

2) 实验测到的齿根应变信号呈现的单、双齿啮合区间的界限没有理论结果明显。这是由于理论模型在啮合区间分布时，将轮齿作为刚体来考虑，而在实际过程中轮齿会发生弹性变形，所以在单、双齿啮合交替的时候存在过渡区域。在过渡区域内，笔者介绍的计算模型不再适用，但这些区域内的齿根应变数值一定位于前后两个稳定啮合区间数值之间。

3) 实验测到的齿根应变信号在每个区间内并不像理论计算结果一样平滑。这是由于理论计算是在平衡状态下进行的，而测试内齿圈齿根应变的工作是在动态工况下进行的，齿轮箱内的误差、齿侧间隙和冲击等因素均会使齿根应变曲线产生波动。

4 结 论

1) 通过仿真计算获得了内齿圈齿根应变在齿宽方向的分布曲线，以及齿根应变在啮合过程中的变化曲线，为测点布置和验证测试方法的有效性提供了理论依据。

2) 从测量原理、测点布置、测量单元设计和测量系统构建等角度对提出的测量方法进行了分析，可以看出该方法与传统方法有较大差异。

3) 搭建了较符合工业现场行星齿轮箱工况条件的实验台，运用所研究的测量系统对行星齿轮箱内齿圈齿根应变进行了测量。实验获得的齿根应变信号与仿真计算的结果无论从单、双齿啮合区间的分布，还是从各区间下齿根应变的数值上均具有较好的一致性，证明了笔者提出的光纤光栅动态测量方法的准确性和有效性。