截面尺寸对B柱抗弯性能影响研究*

覃炳恒 邱贵年 韦学军 刘昌业

(上汽通用五菱汽车股份有限公司 柳州 545007)

0 引 言

在车顶挤压和侧面碰撞中，B柱作为主要的承载部件，抗抵车顶结构和侧面结构发生的大变形，对保护乘员安全和提高车身车顶及侧面结构的抗弯性能起到重要的作用[1]，因此，考虑到B柱抗弯性能对乘员安全和车体变形的影响研究至关重要，B柱的抗弯性能研究一直是车辆侧面碰撞研究中重要课题.胡侃[2]通过改变B柱内外板厚度进行优化进而加强侧面耐撞性.谭耀武[3]利用Hypermesh和Hyperstudy软件对B柱拼焊板及内板的结构进行研究分析并优化.陈新[4]对某型轿车的B柱结构进行优化设计，采用高强度钢结构和拼焊板技术将B柱内外板分成上下两部分进行焊接.上述关于B柱结构方面的研究主要针对B柱加强板、拼焊板和内板进行分析，而对截面形状参数的研究较少.

综上，文中提出从B柱不同截面长宽比对其抗弯性能的研究分析.由于B柱结构复杂，截面形状是不规则的非等截面曲梁，直接研究B柱截面长宽比增大试验和仿真难度，需要将B柱进行截面等效处理.B柱简化模型的截面原型选用胸部位置附近的截面，并验证其有效性.其次对不同截面长宽比的单帽梁样件进行准静态和动态三点弯曲试验及仿真，并进行对比分析，最终得出结论：准静态与动态三点弯曲试验得出规律相同，截面周长一定的情况下，单帽梁的截面长宽比越小其抗弯性能越强.

1 B柱截面等效简化模型——薄壁梁

1.1 B柱截面等效简化模型

通过有限元仿真，讨论B柱孔洞结构、倒角及加强肋、曲面弧度、结构梯度，以及有限元网格大小对三点弯曲结果的影响，最后对B柱结构进行适当的简化设计.在汽车发生侧面碰撞时，考虑乘坐姿势，乘员腹部器官和胸部器官二者当中，腹部器官的损伤对生命的威胁程度相对较低，因为腹部主要是肠，胃等软质的器官，可以承受外界破坏的能力较高.而有研究显示碰撞中的侵入速度对车内乘员肩部和胸部的变形影响比腹部更加显著[5].故B柱简化模型的截面原型选用胸部位置附近的截面.选取某公司某车型B柱截面尺寸作为简化模型薄壁梁的原型截面a，截面尺寸为130 mm×85 mm，焊接边宽15 mm，焊点间距60 mm.其示意图见图1a).考虑到后期部件的加工制造难度，去掉该截面不对称结构，在截面惯性矩不变的前提下删除多余倒角，并将形状调整为单帽型结构截面b，见图2b)，将B柱等效简化为规则的单帽型薄壁梁结构.

1.2 单帽型薄壁梁结构的验证

截面弯曲刚度与样件材料的弹性模量E及截面的惯性矩I有关.根据截面惯性矩尽量保持不变的原则，测量截面a与截面b的周长、面积，以及截面惯性矩，分析以上两个简化截面结构参数的差异，其结果见表1.

图1 B柱截面等效简化前后

表1 简化结构截面参数对比

由表1可知，两个截面的惯性矩数值误差均在5%以内，满足截面惯性矩的误差要求；另外，其周长与面积的误差也均在10%以内，满足工程使用的要求.

1.3 截面尺寸长宽比不同的薄壁梁几何模型

针对截面尺寸长宽比的研究，主要截面类型为单帽型结构，为保证研究过程中内容的单一性与一致性，每种样本点单帽梁的材料780DP、梁长1 000 mm、截面周长430 mm、厚度1.5 mm、焊接边长度15 mm和焊点间距为60 mm，唯一变量为等周长下的截面长宽比.基于初始截面尺寸130 mm×85 mm，挑选了32组长宽比由0.38～5.14的样本点进行仿真模拟.单帽梁的截面尺寸长取值范围60～180 mm、宽取值范围35～155 mm，5 mm为取值间距.

2 准静态三点弯曲试验

2.1 试验方案设计

在万能试验机上对试件进行准静态三点弯曲试验以观察试件的变形过程.试件采用两端简支的支承方式使得B柱相对于压头有相对滑移的现象，且保证了模型结构的完整性，使得准静态三点弯曲试验能够顺利进行[6].其中试验压头高45 mm、直径30 mm，两支撑架之间的跨距820 mm.支座及压头材料均为45号钢.试验中压头下压位移统一为150 mm，同时为了保证薄壁梁在准静态下受压，设置压头恒定加载速度为10 mm/min(仿真时为提高计算速度，取2 mm/ms).试验全程用摄像机记录压头与试件接触处变形情况.

2.2 准静态三点弯曲试验仿真与对标

有限元模型由HyperMesh建模完成，所有的薄壁结构采用四节点的全积分壳单元离散，网格尺寸为5 mm×5 mm.支撑滚柱采用六面体单元模拟，网格大小为10 mm×10 mm，材料模型为Q235.刚性压头可直接通过建立刚性墙Rigidwall来对薄壁梁施加加载力，根据实际压头尺寸，设置刚性墙为半径15 mm、长300 mm的圆柱体形状，并向其施加恒定加载速度2 mm/ms(仿真时为提高计算速度，故将此加载速度适当提高).薄壁结构之间采用点焊的方式连接，即相邻的两部分之间嵌入六面体单元，六面体单元紧贴壳单元的两个面，面积以实际焊点的大小决定，材料设置为MATL100.约束下端的四个底板的全部自由度来模拟试验机的固定工作台.

建模过程中，采用点到面接触模拟焊点与上下两板间的接触，采用自动单面接触模拟薄壁件受压过程中发生的所有接触，以避免在计算过程中互相发生穿透而导致计算中止.薄壁件选用 B400/780DP 材料模型.随后在Control Cards选项里对输出控制设置、沙漏控制、接触控制、计算结束时间、时间步长、输出动画时间步长等进行设置.最终得到模型并将模型导出K文件提交给LS-DYNA求解器计算.图2为准静态三点弯曲试验装置仿真模型与实物图.

图2 准静态三点弯曲试验装置仿真模型与实物图

通过对基础截面的单帽梁进行有限元仿真计算及相应的准静态三点弯曲试验，得到单帽梁的加载力与位移仿真与试验曲线，其对比结果见图3.由图3可知，仿真与试验的两条曲线过程平稳，走势一致，几乎贴合；另外，载荷峰值的误差仅为1.01%，平均载荷的误差也仅为1.35%，各项误差极小.因此，该仿真模型可行且可靠.

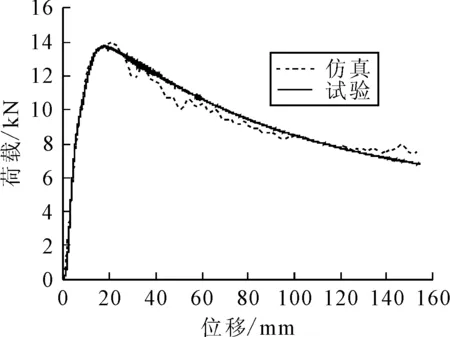
图3 简化单帽梁的位移-载荷仿真与试验曲线对比

2.3 准静态下评价指标的确定

为了更好更方便的研究薄壁梁的抗弯性能，准静态三点弯曲实验从主要以下两个指标进行评判：

1) 平均加载力Fm平均力Fm为加载力曲线在弯曲位移上的算术平均值.它反映的是整个弯曲过程中的整体载荷水平，在薄壁梁弯曲位移一定的情况下，平均加载力的值越大，反映该薄壁梁抗弯性能越强[7-8]，为

(1)

式中：Sf为加载刚性压头的撞击位移；p(s)为加载刚性压头撞击位移为s时瞬态撞击力.

2) 单帽型薄壁梁单位质量所受到的弯矩值(MME)MME为单帽型薄壁梁单位质量所受到的弯矩值，是衡量单帽梁抗弯性能的一个重要参数，MME值越大，表明该薄壁梁的抗弯性能越强，为

(2)

式中：θf为薄壁梁最终的弯曲角度；M(θ)为薄壁梁弯曲角度为θ时瞬态的弯矩值；m为薄壁梁样件的总质量.

2.4 准静态下不同截面长宽比的薄壁梁仿真结果分析

根据选取的32组样本点信息，分别在基础截面单帽梁仿真模型的基础上进行修改调整，完成对32组样本点的有限元模型建立.通过Ls-Dyna软件求解计算，获得32种不同截面长宽比的单帽梁在准静态工况下的抗弯特性，其计算结果统计见图4.

由图4可知，平均加载力、MME等曲线整体的变化趋势一致，即等截面周长的情况下，单帽型薄壁梁受到的平均加载力与MME随截面长宽比的增大逐渐降低.

为了进一步针对长宽比这一影响因素进行对比分析，从仿真样本点中挑选几组最具代表性的不同长宽比样件进行准静态三点弯曲试验.挑选的样件其具体截面尺寸为100 mm×115 mm，107.5 mm×107.5 mm，115 mm×100 mm，125 mm×90 mm，135 mm×80 mm，145 mm×70 mm，并增加一组截面周长不同、长宽比为设置为1、截面尺寸为100 mm×100 mm的单帽梁试验样件.统计试验数据结果见表2.

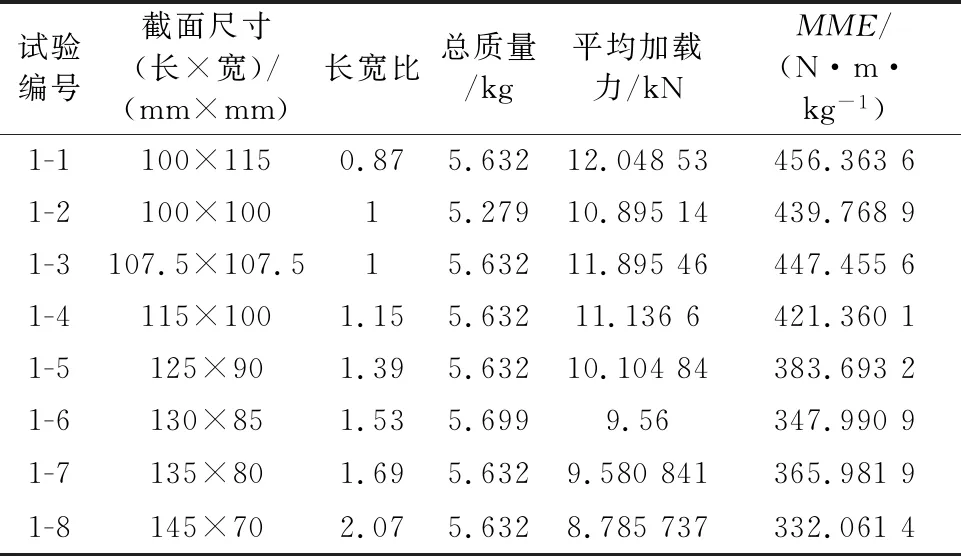
表2 长宽比样本点试验数据统计表

由表2可知,分析截面长宽比对单帽梁抗弯性能的影响.图5为试验中单帽梁所受到的平均加载力及MME值随截面长宽比的变化图.

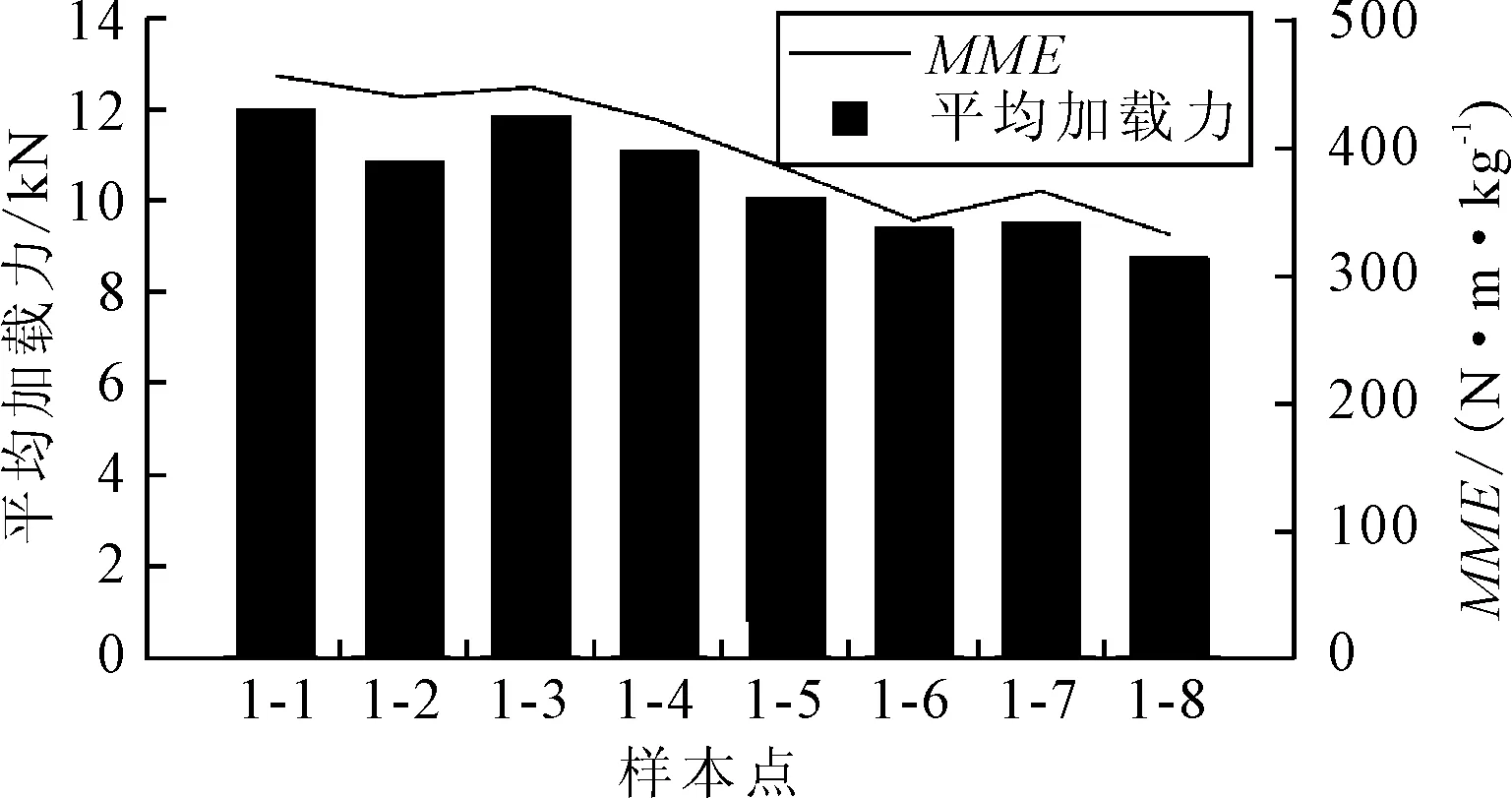
图5 长宽比样本点试验数据变化图

由图5可知，单帽梁准静态三点弯曲试验中平均加载力及MME值随截面长宽比的变化趋势与仿真计算所得到的趋势一致，即等截面周长的情况下，单帽形薄壁梁受到的平均加载力与MME值随截面长宽比的增大逐渐降低.

3 冲击载荷下单帽形薄壁梁结构分析

3.1 动态三点弯曲试验

试验台的结构与准静态三点弯曲试验台大体相同，其相关尺寸与跨距皆与准静态式样相同，与准静态试验不同的是，试验中为防止薄壁梁样件受到冲击弹出试验台架，造成设备损坏及人员伤害，在支撑架上设置了限位装置，限制其侧向运动.信号采集系统包括应变传感器、位移传感器以及高速摄像机.

试验的加载设备为高速落锤试验系统，其锤头最大冲击速度为15 m/s，速度控制精度高达1.0%，锤头底端弧面直径为110 mm，整个落锤结构基础质量为21 kg，配重板单块2 kg，对于不同的薄壁梁样件，所使用的锤头质量也不尽相同.锤头装置与抓取提升装置均有两导轨配合引导，实现快速加载，保证锤头垂直下落并能满足相应的冲击速度，见图6.

图6 动态三点弯曲试验设备

根据C-NCAP对侧面碰撞试验的要求，同样设置锤头的冲击速度为50 km/h，即13.89 m/s，因此，锤头的提升高度设置为10.1 m.为了保证试验中不同单帽形薄壁梁样件之间的可比性，需根据不同的单帽梁结构调整锤头的质量，以保证单帽梁在试验中的弯曲位移至少达到150 mm.

3.2 动态下评价指标的确定

为了更好更方便的研究薄壁梁的抗弯性能，动态三点弯曲实验根据两个主要指标进行评判.

1) 平均加载力Fm同样按照2.3中的平均加载力作为动态三点弯曲试验的抗弯性能指标.

2) 能量比R能量比是由薄壁梁结构在受到冲击载荷至其弯曲位移达到150 mm过程中所吸收的能量除以锤头下落至与薄壁梁结构发生碰撞时的初始能量而得到，R表现了薄壁梁结构在冲击载荷下吸收能量能力，R越大，则该薄壁梁其抗弯性能越弱，为

(3)

式中：E0为锤头下落至与薄壁梁结构发生碰撞时的初始能量；F(s)为薄壁梁结构弯曲位移为s时所受到的瞬态加载力；m0为试验锤头的质量；h为锤头释放的高度，本试验中锤头释放高度均为10.1 m.

3.3 不同截面长宽比的薄壁梁动态冲击下抗弯性能分析

为了分析不同截面长宽比的薄壁梁在动态冲击下的抗弯性能，从表2的样本点中挑选具有代表性的三组进行动态三点弯曲试验，见图7，长宽比样本点动态试验样件图.三组样本点单帽梁其抗弯性能各不相同，为了保证在试验中其弯曲位移均能达到150 mm的指标，根据不同样件的结构调整锤头的质量，具体锤头质量信息、样件尺寸及试验结果见表3.

图7 长宽比样本点动态试验样件图

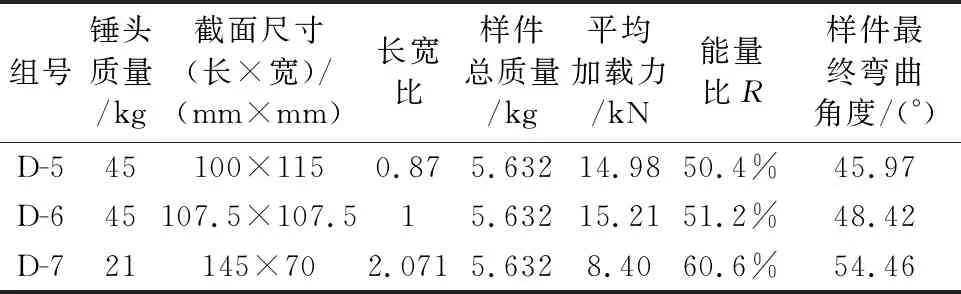
组号锤头质量/kg截面尺寸(长×宽)/(mm×mm)长宽比样件总质量/kg平均加载力/kN能量比R样件最终弯曲角度/(°)D-545100×1150.875.63214.9850.4%45.97D-645107.5×107.515.63215.2151.2%48.42D-721145×702.0715.6328.4060.6%54.46

由表3可知，准静态下三点弯曲试验得到的规律在动态冲击工况下依旧成立，即：等截面周长的情况下，单帽型薄壁梁受到的平均加载力随截面长宽比的增大逐渐降低，另外能量比以及样件的最终弯曲角度都随着截面长宽比的增大而逐渐增大，因此单帽梁的抗弯性能随着长宽比的增加逐渐减弱.

4 不同截面薄壁梁准静态与动态抗弯性能对比分析

为了进一步分析比较不同截面长宽比的单帽梁分别在准静态及动态冲击下的抗弯性能，选取表2中三组样本点，长宽比分别为0.87，1及2.071,将每组单帽梁样件在不同工况下得到的力与位移试验曲线进行对比，见图8.

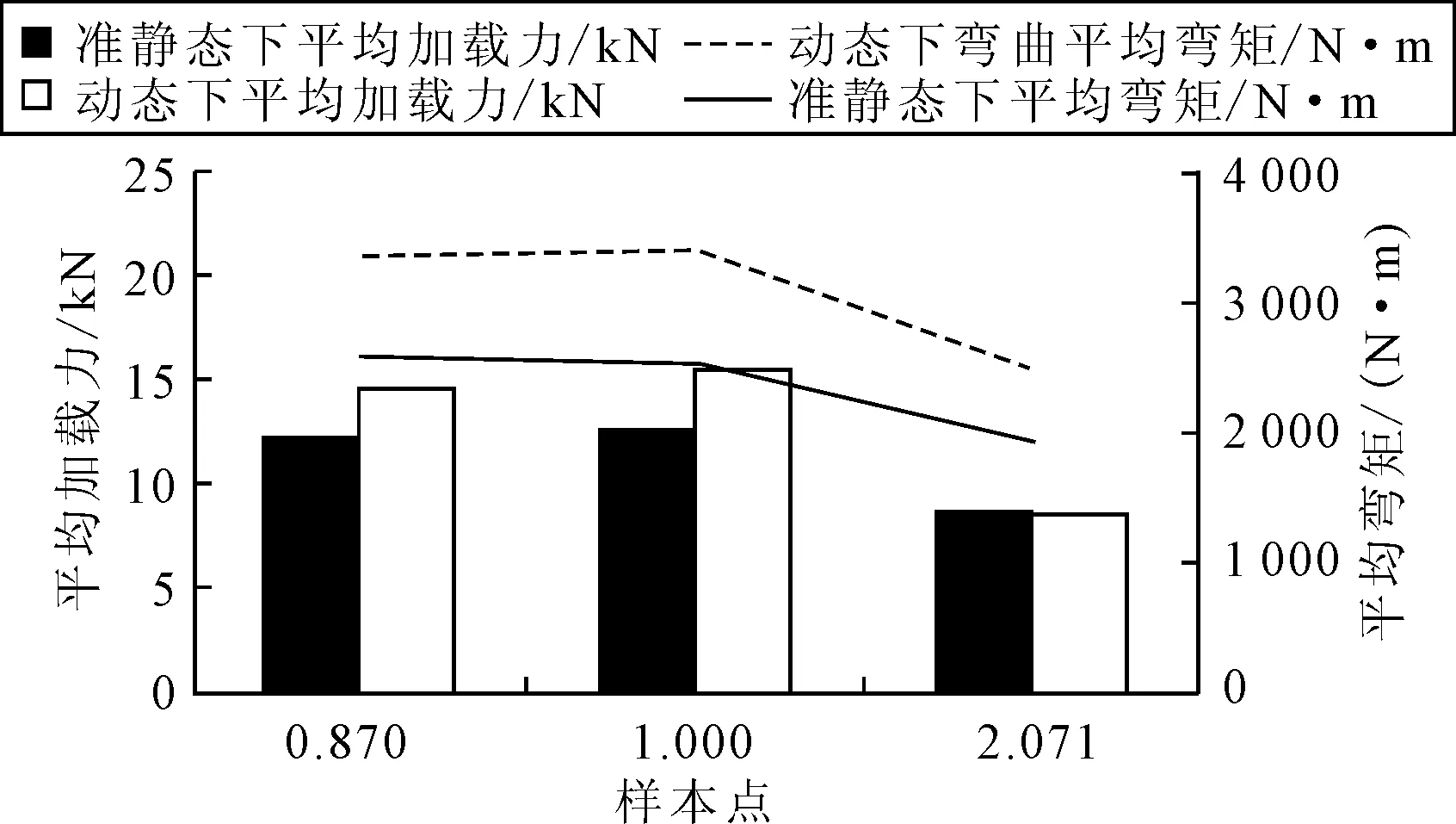
图8 长宽比样本点准静态与动态试验数据变化图

由图8可知，相同单帽梁样件在动态冲击的工况下得到力与位移曲线趋势与准静态下得到的曲线一致，但由于动态冲击下材料的应变率效应，其受到的平均加载力、平均弯矩等评价指标更大，体现出的抗弯性能更强.

5 结 束 语

根据某微型客车B柱模型，选取其关键截面，根据简化前后惯性矩不变原则，将其简化成为单帽型薄壁梁结构，并通过验证简化模型的合理性.为了探究单帽型薄壁梁不同截面长宽比对其抗弯性能的影响规律，进行准静态和动态三点弯曲试验和仿真.综上所述，动态三点弯曲试验下得到的规律与准静态试验相同：截面周长一定的情况下，单帽梁的截面长宽比越小其抗弯性能越强.