时间尺度与选择倾向性协同作用下的演化博弈模型

王西龙 王继成 罗成 田秀霞

摘 要：针对合作行为的涌现与维持问题，基于演化博弈理论和网络理论，提出了一种促进合作的演化博弈模型。该模型同时将时间尺度、选择倾向性引入到演化博弈中。在初始化阶段，根据持有策略的时间尺度将个体分为两种类型：一种个体在每个时间步都进行策略更新;另一种个体在每一轮博弈后，以某种概率来决定是否进行策略更新。在策略更新阶段，模型用个体对周围邻居的贡献来表征他的声誉，并假设参与博弈的个体倾向于学习具有较好声誉邻居的策略。仿真实验结果表明，所提出的时间尺度与选择倾向性协同作用下的演化博弈模型中，合作行为能够在群体中维持;惰性个体的存在不利于合作的涌现，但是个体的非理性行为反而能够促进合作。

关键词：演化博弈;时间尺度;选择倾向性;囚徒困境;复杂网络

中图分类号： TP391.9

文献标志码：A

Abstract： Considering emergence and maintenance of cooperative behavior， based on evolutionary game theory and network theory， an evolutionary game model which can promote cooperation was proposed. In the proposed model， time scale and selection preference were introduced simultaneously into evolutionary game. In initialization phase， players were segmented into two categories according to their time scales of the strategies. Players in one category updated their strategies in each round， while players in the other category determined wether to update their strategies according to certain probability after every round of game. In strategy updating phase， the reputation of a player was determined by his distribution to his neighbors， and all players perfered to learn the strategies of neighbors with good reputation. The simulation experimental results show that， in the proposed evolutionary game model under synergistic effect of time scale and selection preference， cooperative behavior can be maintained in the group， the players with inertia hinders the emergence of cooperation， but the irrational behavior of players can promote cooperation.

Key words： evolutionary game; time scale; selection preference; prisoners dilemma; complex network

0 引言

合作行為在自然界和人类社会中广泛存在。合作会牺牲个人利益给对方带来益处，背叛行为会不劳而获。然而，在由自私个体组成的群体中，合作是怎样涌现与维持的呢？ 研究合作的本质，有助于认识从生命的起源到人类社会的组织等一系列重要的课题，为以后对网络上的动力学过程进行定性调控乃至精确控制打下坚实的基础。因此，合作动力学研究已经成为复杂网络的一个热门研究方向。

演化博弈理论为研究合作的动力学提供了有力的理论基础。学者们基于演化博弈理论对合作行为进行了大量的研究，促进了该学科的发展[1]。Nowak等[2-3]率先在方格网络上进行重复囚徒困境研究，发现背叛行为会逐渐蔓延开来，网络会进化成优美的斑图，合作者会抱团，结成紧密的合作簇来抵御背叛行为的入侵。

近年来，将某些社会现象引入到演化博弈模型中研究合作的涌现机理成为一个研究热点。人类的决策行为具有惰性，不一定在每次博弈后及时更新策略。文献[4]发现，过快或过慢的策略更新时间尺度都不利于合作行为的涌现，而是有一个适中值使得合作水平最高。文献[5]发现，当个体的策略更新时间尺度根据历史信息改变的话会促进合作。文献[6]研究了有孤立个体存在的演化模型中惰性行为对合作的影响，发现个体的惰性会阻碍合作的涌现。

考虑到个体间相互影响的差异性，文献[7]在模型中引入了偏好选择，个体被学习的次数越多则该个体的影响力越大，研究发现该机制能够促进合作。文献[8]发现，当个体倾向于学习收益高的邻居策略时候会促进合作;反之会降低合作水平，甚至合作湮灭。文献[9]发现，在系统演化的过程中，个体的声誉明显地降低了个体被剥削的风险，从而使得合作在演化过程中占主导地位。文献[10]在策略更新时同时考虑个体的声誉和行为的多样性，发现自调节的声誉分类能够明显促进合作。文献[11]提出的演化博弈模型中，声誉好的人可以获得奖励，声誉低的人会受到惩罚，研究发现该机制能够促进合作。

考虑到人们获取信息会有局限性，文献[12]在适应度评价中引入噪声，研究发现该机制能够促进合作，并且有一个适中的噪声值，使得合作的水平最高。文献[13]在有敲诈个体存在的结构化系统中研究个体的理性程度对合作行为的影响，发现：当个体是完全理性时，合作者难以抵御背叛行为的入侵;当个体非常不理性时，会导致合作湮灭;而当个体是有限理性时，能够明显促进合作。文献[14]在模型中假设收益高的个体对收益低的邻居产生同情心，引入了收益的重新分配机制，研究发现该机制能够促进合作。

現有研究提出的演化博弈模型中，虽然很多研究引入了偏好选择、声誉等因素，但是都没有考虑以个体对周围邻居的贡献水平作为衡量声誉的指标，没有研究学习贡献型邻居对合作动力学的影响;而在现实社会中人们往往更倾向于学习对群体有贡献的个体的行为，因此，研究偏好学习贡献型邻居策略对合作的影响具有重要的现实意义。虽然很多研究涉及了策略更新时间尺度、噪声等对合作行为的影响，但是有关两种或多种因素协同作用下合作行为的动力学特点的研究却极少;而现实社会中人们的行为具有多样性，个体的决策会受到多种行为特征的影响，因此，研究多种因素协同作用下的合作动力学特点非常有意义。

针对上述问题，基于演化博弈理论，本文提出了一种引入了策略更新时间尺度与选择倾向性的演化博弈模型。该模型在方格网络上进行重复囚徒困境博弈，研究当相互作用网络与策略学习网络存在时间尺度差异性、个体具有偏好选择的情况下合作行为的动力学特征，并考察了噪声对合作的影响。

1 本文模型与动力学

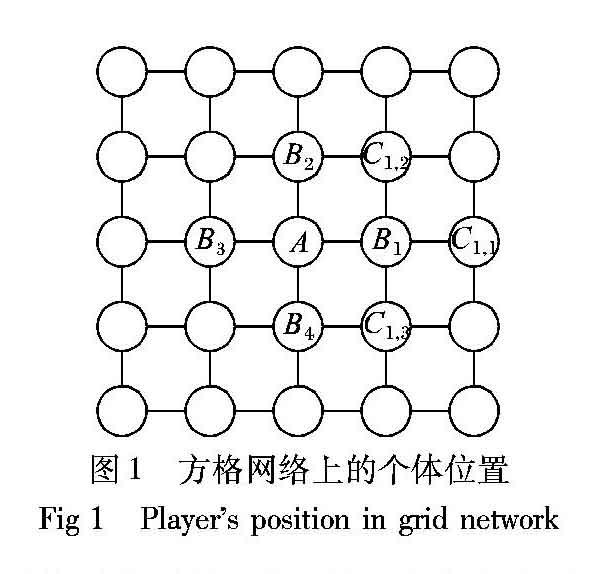
本文模型在L×L 的具有无流边界的方格网络上进行空间囚徒困境博弈。收益矩阵根据Nowak等[2]提出的弱囚徒困境进行取值，将囚徒困境的收益矩阵修改为：令P=S=0，R = 1，并且1

在模型初始化时候，将个体属性分为两种：第一种个体的相互作用网络与策略学习网络时间尺度相同，个体在每一轮博弈之后就进行策略更新，为了表示方便，将其命名为“普通”个体。第二种个体的相互作用网络与策略学习网络存在时间尺度差异，将其命名为“惰性”个体，这类个体在每轮博弈之后，并不一定立即进行策略更新，而是以一定的概率来决定是否进行策略更新。在博弈的初始状态，每个个体以50%的概率被随机地赋予合作或背叛策略。在每一个时间步中，每个个体分别与他最近邻的四个邻居进行囚徒困境博弈，取得累积收益，然后进行策略更新。

在策略更新阶段，为了表征现实社会中人们不一定很快改变原有策略的惰性，将个体分为“惰性个体”与“普通个体”两种类型：将比例为 prop的个体设定成具有惰性的个体，他们在每次博弈之后以一定的概率来决定是否更新策略，这里用变量scale表示更新策略的概率。另一部分个体在每次博弈后都进行策略更新，这部分普通个体的比例为1-prop。这里prop与scale是两个可以调节的参数，prop表征了群体中具有惰性个体的规模;scale表征了个体持有当前策略的时间尺度，其倒数为个体持有当前策略的周期。因为不能主观地假定惰性个体在人群中的分布具有某种规律，本文认为惰性个体应完全无规律地分布在全体参与博弈的群体中。为了表征这种无规律，采用了泊松过程来随机抽样惰性个体。关于泊松过程及其对无规律分布的论述见文献[15]。惰性个体更新策略的速度用变量scale表示。scale的值越大，则更新策略的速度越快：当scale越接近1，该惰性个体越接近普通个体;反之，若scale=0，则该个体永远不更新策略。

在进行策略更新的时候，考虑到现实社会中人们会自发地学习榜样的行为，为了模拟这种现象，本模型中个体倾向于模仿对群体有贡献的邻居的策略。如果邻居的四个邻居收益总和越高，那么他对群体的贡献越大。具体来说，如图1所示。

在选择模仿对象时候，设A是一个参与者，他的四个邻居为B1、B2、B3、B4，并设Bi的邻居为Ci，1、Ci，2、Ci，3、Ci，4，则模型将Bi推荐给A的概率正比于exp{K1[P（Ci，1）+P（Ci，2）+P（Ci，3）+P（Ci，4）]}，其中，K1是一个可以调节的参数，P（Ci，j）表示参与者Ci，j的收益。当Bi被推荐给A后，如果A是非惰性个体，则采用费米动力学（式（2））的计算方法来确定A是否采用Bi的策略。如果A是惰性个体，则A以概率scale决定是否进行策略更新，如果不进行策略更新就保持原有的策略不变;如果决定进行策略更新，则采用费米动力学的计算方法来确定A是否采用Bi的策略。

3 结语

合作行为的涌现与维持机制是近年来的研究热点。本文提出了一种模型，将策略更新时间尺度引入到偏好选择的演化博弈模型中，研究了时间尺度与偏好选择共同作用下合作行为的动力学特点。策略更新的时间尺度用惰性个体的比例、惰性程度的大小来表征;个体在学习邻居策略时候偏好学习声誉高的个体策略。实验结果表明，该模型能够维持系统中的合作行为;而惰性个体的存在，能够在一定程度上阻碍合作行为的涌现;噪声的引入，即个体由完全理性转变为有限理性的情况下，反而能够促进合作。本文的研究工作有助于进一步了解合作的动力学特点。

参考文献 （References）

[1] 荣智海，吴枝喜，王文旭.共演博弈下网络合作动力学研究进展[J].电子科技大学学报，2013，42（1）：10-22.（RONG Z H， WU Z X， WANG W X. Research on the networked cooperative dynamics of coevolutionary games [J]. Journal of University of Electronic Science and Technology of China， 2013， 42（1）： 10-22.）

[2] NOWAK M A， MAY R M. Evolutionary games and spatial chaos [J]. Nature， 1992， 359（6398）： 826-829.

[3] NOWAK M A， MAY R M. The spatial dilemmas of evolution [J]. International Journal of Bifurcation and Chaos， 1993， 3（1）： 35-78.

[4] WU Z X， RONG Z H， HOLME P. Diversity of reproduction time scale promotes cooperation in spatial prisoners dilemma games [J]. Physical Review E： Statistical， Nonlinear， and Soft Matter Physics， 2009， 80（3 Pt 2）： 036106.

[5] RONG Z H， WU Z X， CHEN G R. Coevolution of strategy-selection time scale and cooperation in spatial prisoners dilemma game [J]. Europhysics Letters， 2013， 102（6）： 68005.

[6] JIA D Y， JIN J H， DU C P， et al. Effects of inertia on the evolution of cooperation in the voluntary prisoners dilemma game [J]. Physica A： Statistical Mechanics and its Applications， 2018， 509： 817-826.

[7] WU Z X， XU X J， HUANG Z G， et al. Evolutionary prisoners dilemma game with dynamic preferential selection [J]. Physical Review E： Statistical， Nonlinear， and Soft Matter Physics， 2006， 74（2）： 021107.

[8] WANG Z， PERC M. Aspiring to the fittest and promotion of cooperation in the prisoners dilemma game [J]. Physical Review E： Statistical， Nonlinear， and Soft Matter Physics， 2010， 82（2 Pt 1）： 021115.

[9] XIA C Y， DING S， WANG C J， et al. Risk analysis and enhancement of cooperation yielded by the individual reputation in the spatial public goods game [J]. IEEE Systems Journal， 2017， 11（3）： 1516-1525.

[10] CHEN M H， WANG L， SUN S W， et al. Evolution of cooperation in the spatial public goods game with adaptive reputation assortment [J]. Physics Letters A， 2016， 380（1/2）： 40-47.

[11] GUO H， CHU C， SHEN C， et al. Reputation-based coevolution of link weights promotes cooperation in spatial prisoners dilemma game [J]. Chaos， Solitons & Fractals， 2018， 109： 265-268.

[12] ZHANG G Q， HU T P， YU Z. An improved fitness evaluation mechanism with noise in prisoners dilemma game [J]. Applied Mathematics & Computation， 2016， 276： 31-36.

[13] XU X， RONG Z， TSE C K. Bounded rationality optimizes the performance of networked systems in prisoners dilemma game [C] // ISCAS 2018： Proceedings of the 2018 IEEE International Symposium on Circuits and Systems. Piscataway， NJ： IEEE， 2018： 1-5.

[14] LI Y M， ZHANG J， PERC M. Effects of compassion on the evolution of cooperation in spatial social dilemmas [J]. Applied Mathematics and Computation， 2018， 320： 437-443.

[15] GERARDI A， TARDELLI P. Stochastic control methods： hedging in a market described by pure jump processes [J]. Acta Applicandae Mathematicae， 2010， 111（3）： 233-255.

[16] SZABG， TKE C. Evolutionary prisoners dilemma game on a square lattice [J]. Physical Review E： Statistical， Nonlinear， and Soft Matter Physics， 1998， 58（1）： 69-73.