设置摩擦阻尼耗能框架结构地震反应分析

张敏*,2，汪东卓，庞华英，陈豆豆

(1.广西科技大学土木建筑工程学院， 广西柳州545006;2.江西科技师范大学建筑工程学院， 江西南昌330013)

0 引言

传统的建筑结构通过增强结构本身强度、刚度、延性来抵抗地震作用，对结构本身造成了较大且不可恢复的损伤。鉴于此，不少学者相继提出了各种增强结构自我调节能力且积极主动的结构减震方法,从而产生了工程结构减震控制技术[1]。耗能减振是结构减震控制的一种，通过在结构中设置附加减震装置，来代替结构抵抗和消耗大部分的地震能量，从而降低结构的地震作用和损伤[2]。

摩擦阻尼器是一种性价比较高的减震装置，其摩擦力可通过调节摩擦型高强螺栓预紧力大小来控制[3-4],且产生的摩擦热对其耗能属性没有影响；且因其价格低廉、构造简单、性能稳定、耗能能力强，可较大抵御和消耗地震及风荷载输入结构的能量，最终达到减少结构地震响应的目的，因而在实际工程设计中较为常用。

国内外很多学者对摩擦阻尼器的减震性能进行了分析研究。1980年Pall和Marsh首先设计出限位滑移螺栓节点(limited slip bolted joint, LSB)和Pall摩擦耗能器[5-6]。1988年，陈宗明等研制开发出了摩擦剪切耗能器，其工作原理为通过高强螺栓在滑移槽中水平运动产生摩擦力来消耗和吸收地震能量[7]，试验结果表明：当整个框架侧移时，摩擦阻尼器上、下水平板间的滑动量几乎与楼层层间侧移相同；当高强螺栓滑动时，杆件内力主要由摩擦阻尼器的摩擦力引起，变化不大，保持在弹性范围内，滞回曲线较饱满，为较理想的弹塑性曲线，且能够在较大位移的范围内反复耗能。Chung等[8]提出了在连梁跨中设置摩擦阻尼器从而降低高层钢筋混凝土结构的地震反应，并通过数值模拟验证了摩擦阻尼器的有效性能。2001年，李惠等[9]对向心式变摩擦耗能器的工作原理及力学分析模型进行了验算和研究。2010年，彭凌云等[10]提出一种拟线性摩擦阻尼器,经过研究分析得：该阻尼器提供近似线性滞回阻尼,其阻尼力的大小与位移量近似成正比,阻尼力的方向与速度同向。2014年，Raut等[11]以20层高的钢铁建筑为研究对象，在建筑中安装摩擦阻尼器，考虑El-Centro等地震波作用，分析表明,摩擦阻尼器的激活取决于滑移力,适当的滑移力和合适位置,可以有效降低建筑结构的地震响应。

本文对设置摩擦阻尼器的框架结构减震性能进行分析，给出含有摩擦阻尼器的振动方程，由此研究各楼层设置摩擦阻尼器框架的地震响应，以各楼层的楼层位移和层间最大位移角作为衡量因素进行分析；进而研究了摩擦阻尼器在结构楼层中的经济布置方案；分析该减震结构的地震作用计算方法，在此基础上，对设置摩擦阻尼器结构分析了其等效阻尼。

1 摩擦阻尼器模型

本结构采用的摩擦阻尼器为摩擦剪切耗能器，如图1～图3所示。当框架侧移时，摩擦阻尼器上、下侧板间的滑动量与楼层层间侧移相同。

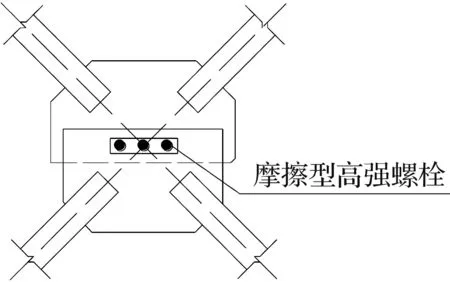
图1 摩擦阻尼器构造Fig.1 Friction damper construction

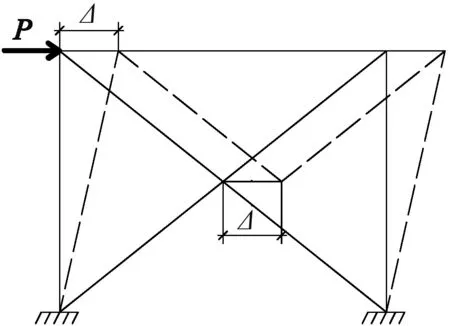
图2 摩擦阻尼器工作原理图
Fig.2 Working principle diagram

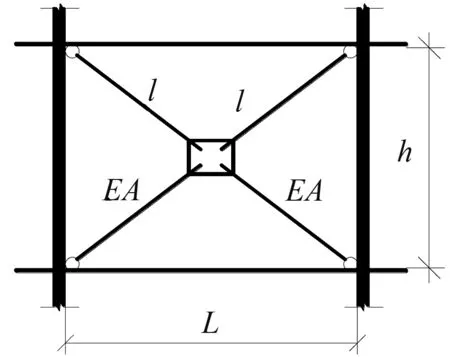
图3 摩擦阻尼器分析模型
Fig.3 Calculation model diagram

图中E为摩擦阻尼器斜支撑杆件的弹性模量；A为单根摩擦阻尼器斜支撑杆件的横截面积；L为摩擦阻尼器所在跨间的楼层净跨度；l为摩擦阻尼器斜向支杆的长度。

2 地震作用响应分析

2.1 状态方程直接积分法

建筑结构中设置摩擦阻尼器作为阻尼耗能减振装置时，结构振动方程为：

(1)

式中:

[M]、[C]、[K]分别为结构的自身质量矩阵、自身阻尼矩阵、自身刚度矩阵；

{Fd}为摩擦阻尼器的作用力向量；

{x}为各楼层相对于结构基础的位移向量；

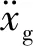
第i楼层摩擦阻尼器的作用力为：

(2)

式中：

式中：fi为第i楼层摩擦阻尼器的摩擦力；kdi为第i楼层摩擦阻尼器支撑杆件轴向刚度；

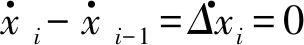
由式(2)得：

(3)

式中：[I]为n×n单位矩阵；

[ηKd]为摩擦阻尼器支撑杆件形成的附加刚度矩阵。

故振动方程可写为：

(4)

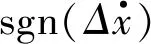
假设时间间隔Δt内，第i楼层速度为:

(5)

同理，第i-1楼层速度为：

(6)

第i楼层相对第i-1楼层速度为：

(7)

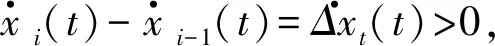
(8)

(9)

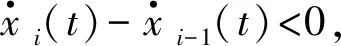
(10)

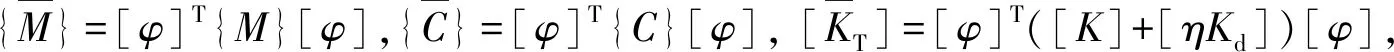
(11)

可得状态方程为：

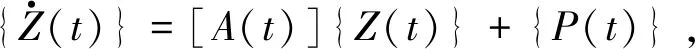
(12)

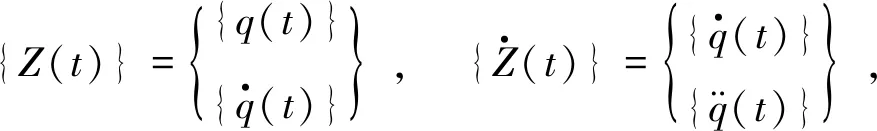
(13)

求解方程(12)，可得ti时刻的状态向量：

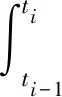
(14)

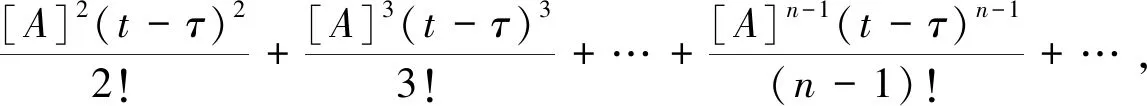
(15)

采用Cotes积分法，则：

(16)

可得：

(17)

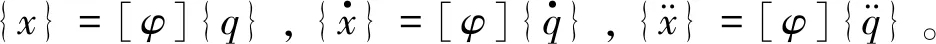
(18)

2.2 地震作用分析

建筑结构设置摩擦阻尼器后，由于阻尼的作用较显著，阻尼不宜忽略，结构各楼层地震作用为：

{F}=[K]{x},

(19)

将{x}=[φ]{q}代入式(17)中，经变换，可得:

{F}=[M][φ][ω2]{q},

(20)

(21)

(22)

式中ωnj为框架结构第j振型的振动频率。

当仅考虑第j振型，则结构地震作用幅值为：

(23)

故第j振型第i质点的地震作用幅值为：

(24)

3 摩擦阻尼器的等效阻尼

结构设置摩擦阻尼器后，阻尼分布较复杂，如何确定该结构的等效阻尼？从而能便捷地采用《建筑抗震设计规范》地震反应谱计算该结构地震作用，这是本文需要研究的问题。

摩擦阻尼器是一种位移相关性阻尼器，可将其等效为阻尼力与速度成正比的粘滞阻尼器，由此分析摩擦阻尼器的等效阻尼比。

3.1 摩擦阻尼耗能

(25)

{Fd}={Fd1,Fd2,…,Fdn},

(26)

Fdi=fdi-fd(i+1),

(27)

式中：{Fd}为结构各楼层的摩擦阻尼力向量；fdi为第i楼层阻尼器阻尼力。

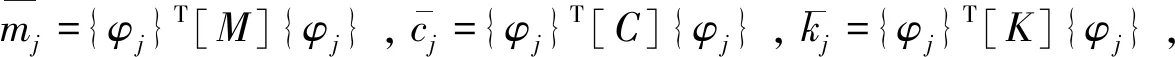
(28)

对式(28)两边各项分别积分，则得：

(29)

式(29)中，等式左边四项分别代表结构第j振型振动时的动能、结构自身阻尼耗能、结构弹性势能和阻尼器摩擦阻尼耗能；等式右边代表地震输入结构的能量。

第j阵型一个周期摩擦阻尼耗能为:

(30)

将式(2)代入式(30)中，得:

(31)

通过化简，得：

(32)

式中fi为第i楼层阻尼器的阻尼力绝对值，fi=|fdi|；

qjm为第j振型正则坐标qj的幅值；

考虑摩擦阻尼器斜支撑的刚度，则：

(33)

式中：

kbi,kb(i+1)分别为第i楼层，第(i+1)楼层摩擦阻尼器支撑杆件的水平刚度。

3.2 等效阻尼比

阻尼按如下原则等效：

①阻尼耗能总量不变；

②结构各阶正则坐标幅值不变。

摩擦阻尼等效为粘滞阻尼后，第j阵型一个周期耗能为：

(34)

式中：

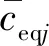
ξeqj为第j振型等效阻尼比,ωnj为第j振型结构自振频率；

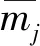
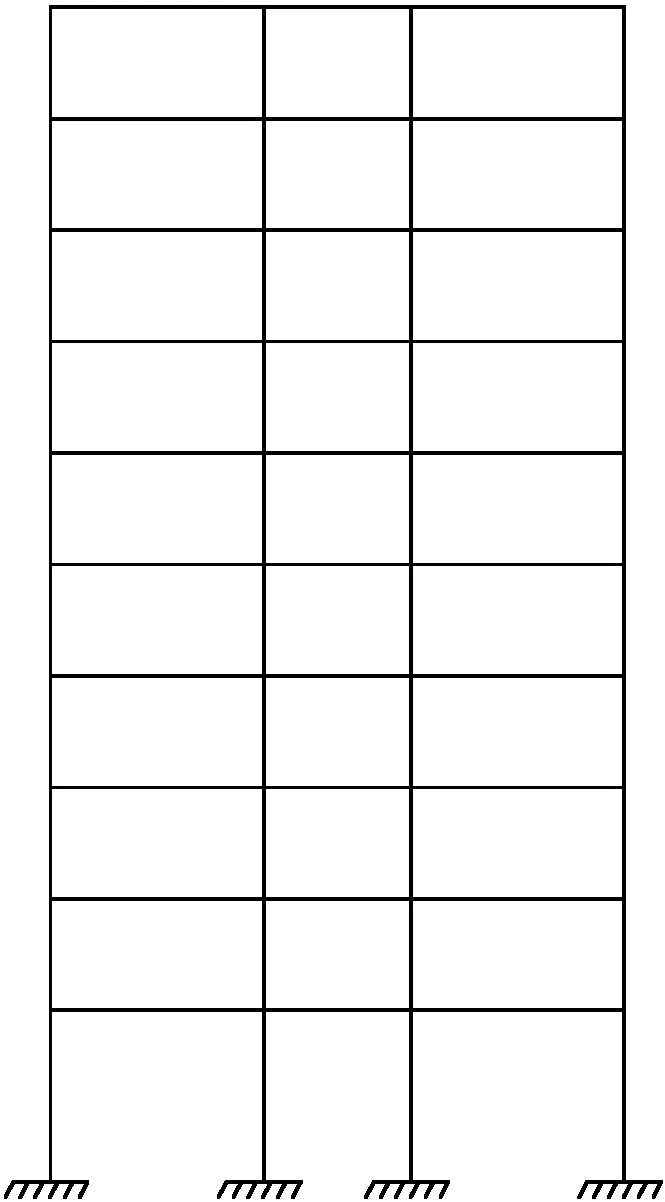
令qj=qjmsin(ωjt+ψj)，可得：

(35)

由此得结构第j振型等效阻尼比:

(36)

式中：Amax为地震波加速度幅值,ω为场地卓越频率,γj为结构第j阵型参与系数。

4 工程实例

该算例为一栋钢筋混凝土框架结构的建筑物，建筑物总高度为34.2 m，共10层，首层高度为4.5 m，其余各层高度均为3.3 m，结构平面如图4所示；该框架抗震设防烈度为8度(0.30 g)，地震分组为第2组，设防类别丙类；结构自身阻尼比为ξn；梁、板、柱混凝土强度等级均为C30；各框架柱截面尺寸为600 mm×750 mm，各框架梁截面尺寸为300 mm×650 mm，各楼层重力荷载代表值均为1 176 kN；框架结构计算见图5，结构分别沿横向按图5(a)～(e)布置摩擦阻尼器。各摩擦阻尼器的滑动摩擦力f均为100 KN，每根摩擦阻尼器斜支撑截面为Q235钢2L45×5。

本文分别考虑四种地震波，即：OROVILLE波、EL-Centro波、HOLLYWOOD STORAGE波、天津波。根据《建筑抗震设计规范》(GB 50011—2010)[12]各地震波的加速度峰值均为110 gal。

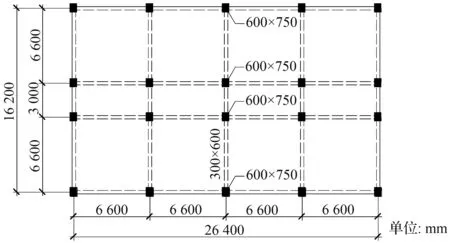
图4 框架结构平面布置
Fig.4 Plane layout of frame structure

(a)(b)(c)(d)(e)

分别按本文状态方程直接积分法和SAP2000软件分析，结果如下：

4.1 结构楼层相对基础的最大位移响应

图6中粗线表示按照本文的状态方程直接积分法的进行数值模拟的分析结果，相应细线表示SAP2000软件分析结果(以下均同)。通过比较两种方法所得的计算结果基本相同。

图6表明：

①当结构仅第一层布置摩擦阻尼器[图5(b)]时，在四种地震波作用下，结构底层的楼层最大侧移反应相对于抗震结构[图5(a)]均有较大减小，但在第二楼层位移反应增长较快。

②当结构在第1到第3层布置摩擦阻尼器[图5(c)]，结构各楼层最大侧移反应相对抗震结构[图5(a)]均有较明显的减小，但在第四楼层位移反应增长较快。

③当结构各层除第六层外均布置摩擦阻尼器[图5(d)]，各楼层位移反应大大减小，但在无阻尼器的第六层楼层位移反应增长较快。

④当结构各楼层均匀布置摩擦阻尼器[图5(e)]，其各楼层最大侧移反应相对相应抗震结构[图5(a)]均减小较大，约为抗震结构的(25 %～35 %)，减震效果较为显著，且各楼层位移反应分布较均匀，未出现突变现象。

结构在楼层设置摩擦阻尼器后，阻尼器对其所在楼层施加了一个阻尼力，该阻尼力将降低其所在楼层的位移反应，但对其他楼层位移反应影响较小，因此当阻尼器在结构楼层分布不均匀时，楼层的层间位移分布也不均匀。

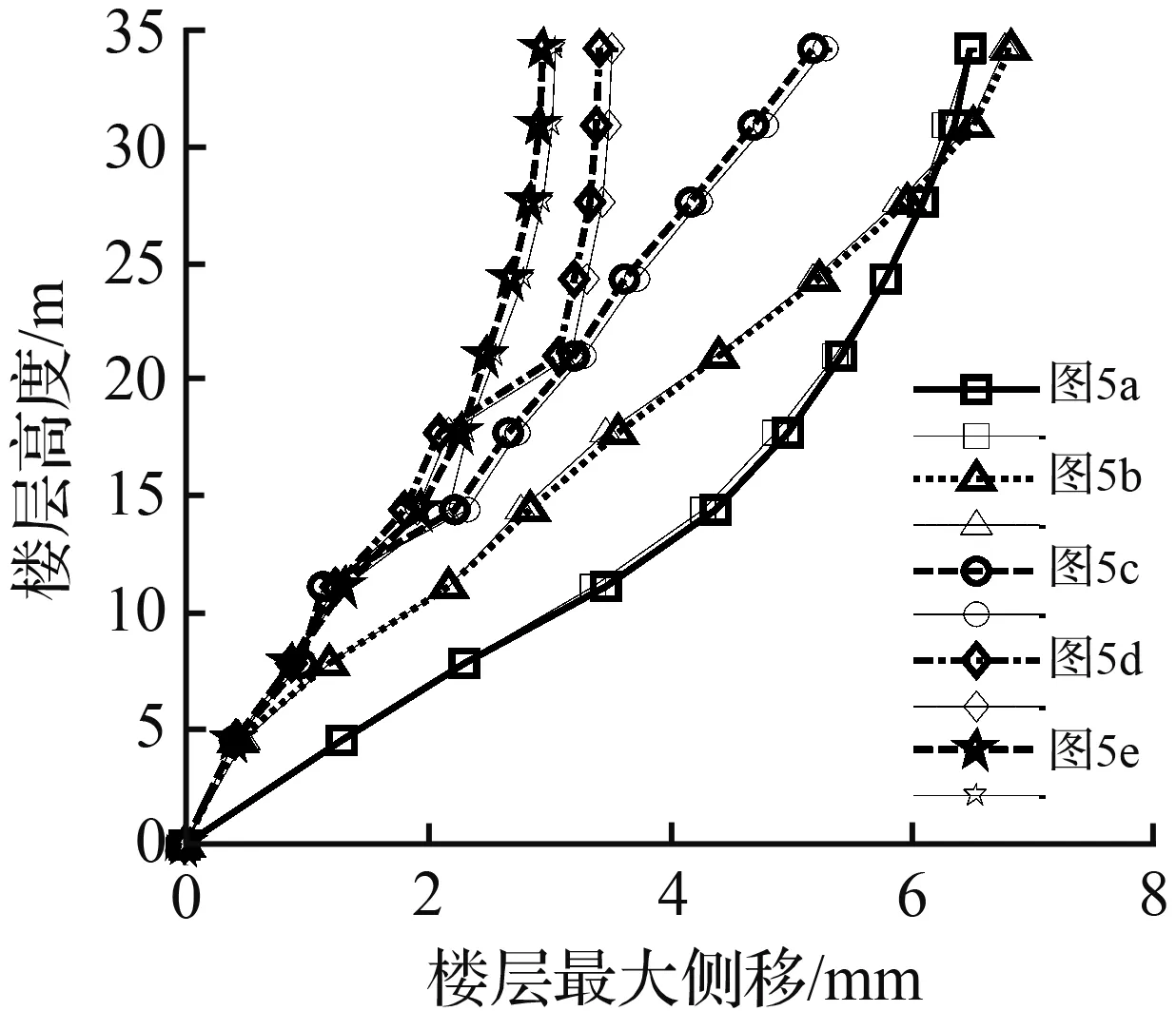
(a) OROVILLE地震波 (b) EL-Centro地震波

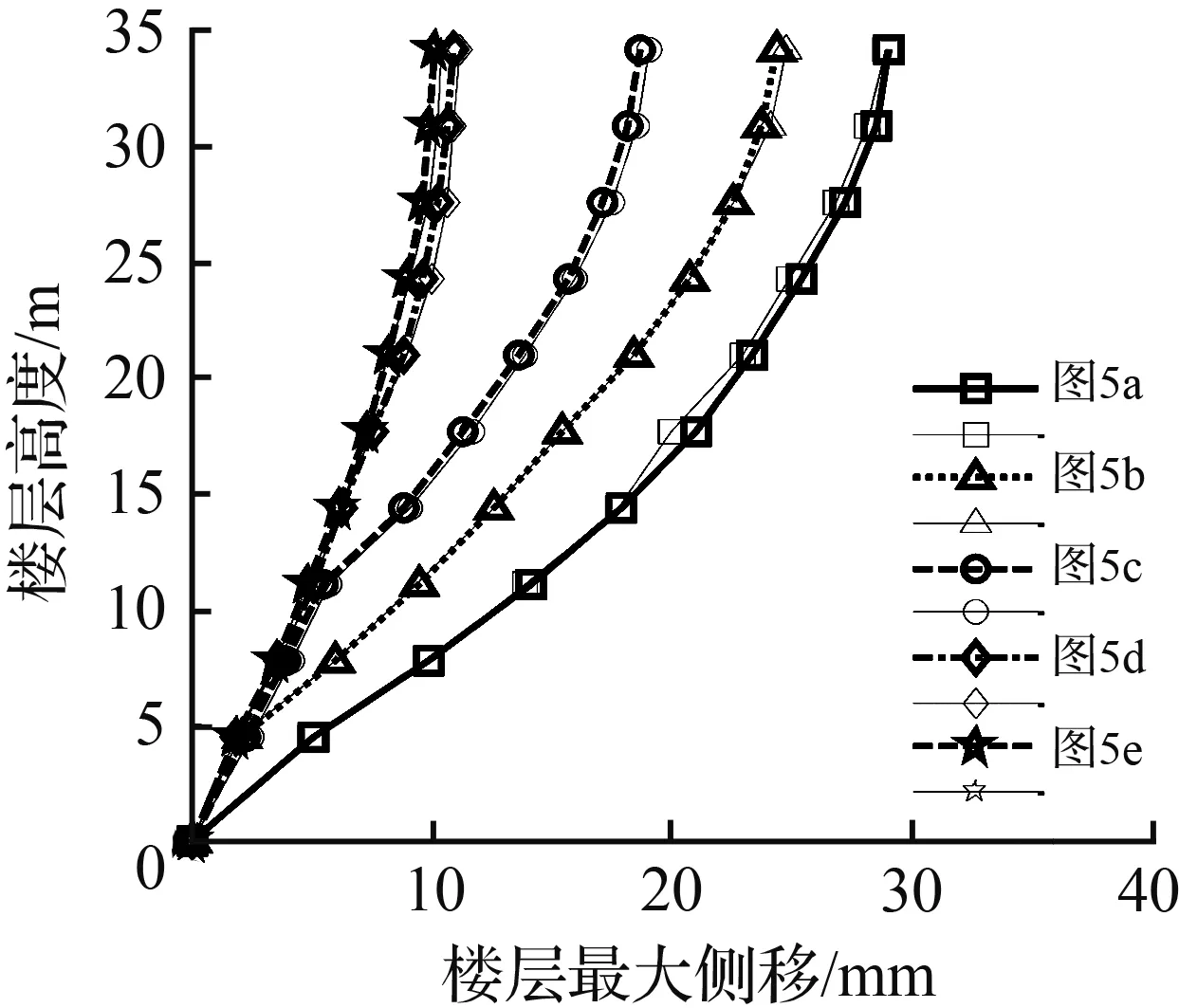
(c) HOLLYWOOD STORAGE地震波 (d) 天津地震波

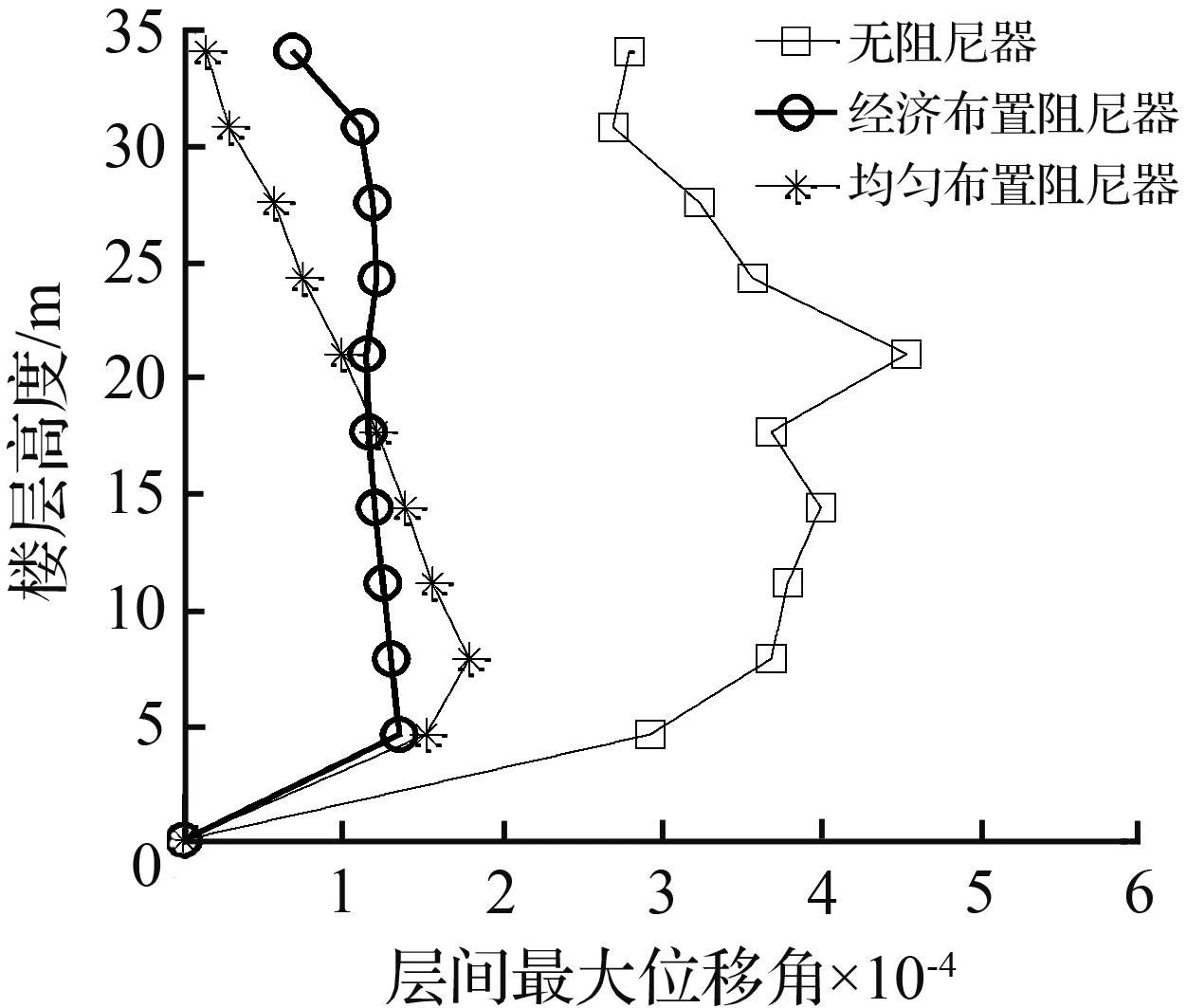
4.2 结构层间最大位移角响应

由图7可见：

①当楼层布置摩擦阻尼器时，与相对应的抗震结构图5(a)比较，其层间最大位移角显著减小，而楼层未布置摩擦阻尼器时，其层间最大位移角相对抗震结构图5(a)减小不多，甚至会超过抗震结构图5(a)的层间最大位移角；

②当楼层均匀布置摩擦阻尼器时图5(e)，与相对应的抗震结构图5(a)比较，其层间最大位移角显著减小，且结构由下至上各楼层的层间最大位移角基本呈递减的趋势，表明按照该方案布置摩擦阻尼器时，能较大的减小结构的地震作用，具有较好的减震效果；

③当结构各层除第六层外均匀布置摩擦阻尼器时图5(d)，除第六层其他各层的减震效果都较好，而未布置阻尼器的第六层层间最大位移角发生突变，其值甚至达到相应抗震结构相应楼层的相应值，因此各楼层阻尼器布置宜连续布置不宜间断；

上述分析表明，摩擦阻尼器仅对其所在楼层的减震较为有效，对其他楼层的减震效果影响不大。这是由于地震作用下楼层设置摩擦阻尼器，会降低所在楼层的层间位移角，但对未设置摩擦阻尼器的楼层，由于楼层层间位移与层间速度不完全同步，造成其他楼层摩擦阻尼器有可能增大未设置阻尼器楼层的层间位移角，因而该结构的层间位移角分布不均匀。

4.4 摩擦阻尼器阻尼力的经济分布分析

以上分析表明，当阻尼器在各楼层均匀布置时，减震效果较好，但各楼层的层间最大位移角分布不均匀。框架结构上部楼层的层间剪力与层间最大位移角一般均较下部楼层相应值小，若摩擦阻尼器在各楼层中均匀布置，则摩擦阻尼器阻尼力的设置不够经济，因而本文提出适当减小上部楼层的阻尼力，使各楼层层间最大位移角分布接近，既可以满足地震作用层间最大位移角限值的要求，又能达到经济合理的目的。

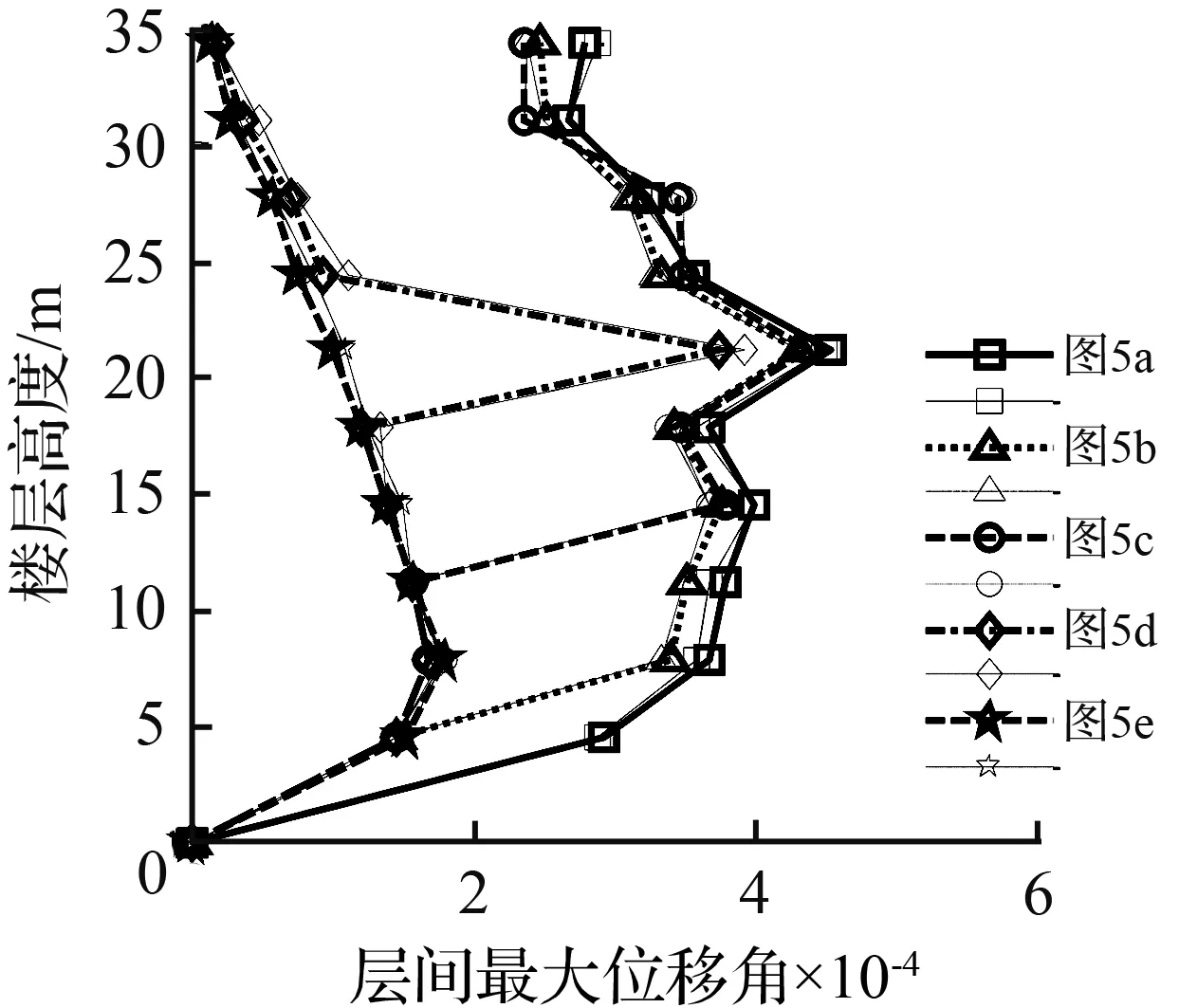
(a) OROVILLE地震波(b) EL-Centro地震波

(c) HOLLYWOOD STORAGE地震波(d) 天津地震波

以图5(e)摩擦阻尼器在各楼层均匀布置方案的层间最大位移角为标准，各楼层阻尼器的阻尼力f按下式调整：

(37)

式中:fi+1,fi分别为结构第i+1、第i楼层摩擦阻尼器的阻尼力；Δθi+1,Δθi分别为各楼层摩擦阻尼器均匀设置时，第i+1、第i楼层的层间最大位移角。

将图5(e)中均匀布置的摩擦阻尼器阻尼力按式(37)调整，计算结果见表1。

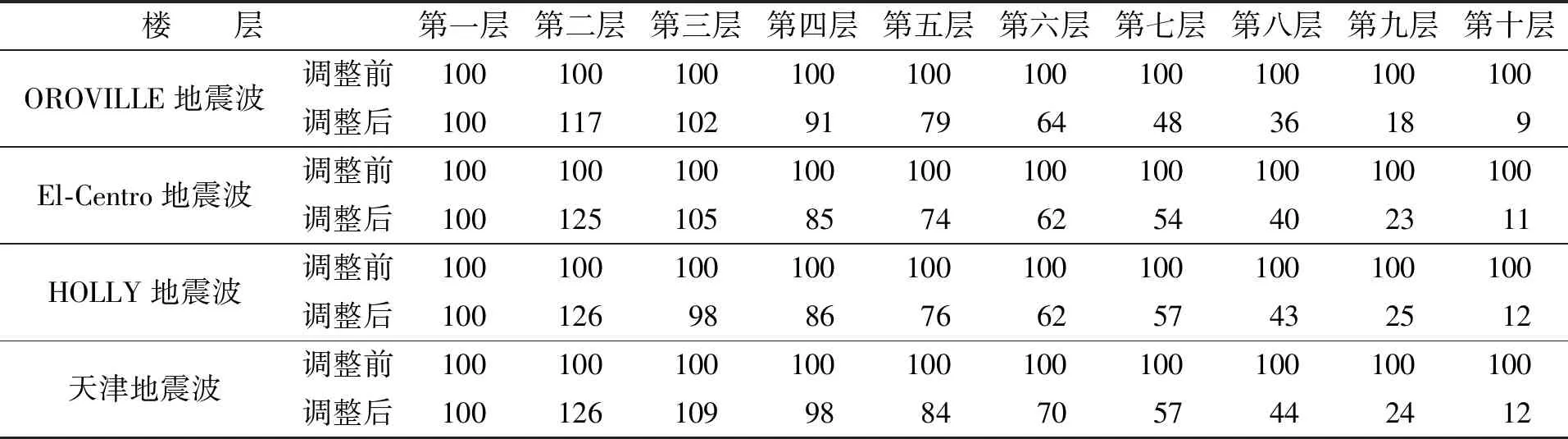
表1 各楼层摩擦阻尼器的阻尼力Tab.1 Damping force of each floor kN

分析表明，调整前后各楼层的最大侧移及层间最大位移角分别见图8、图9。

图8、图9分别显示了各楼层均匀布置摩擦阻尼器时，并对阻尼力按式(37)调整后的各楼层最大位移及层间最大位移角。可见调整后，楼层摩擦阻尼力较均匀布置时减小，且各楼层层间最大位移角差别减小，并且下部较多楼层的层间位移角比较接近，因而在满足设计规范的条件下，调整后各楼层阻尼器的阻尼力分布不仅安全，而且较为经济合理。

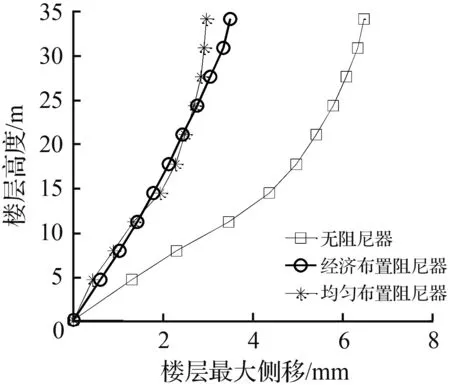
(a) OROVILLE地震波(b) EL-Centro地震波

(c) HOLLYWOOD STORAGE地震波(d) 天津地震波

(a) OROVILLE地震波(b) EL-Centro地震波

(c) HOLLYWOOD STORAGE地震波(d) 天津地震波

4.4 地震作用实用计算

楼层各阻尼器的阻尼力按公式(37)调整后，结构地震作用按式(24)计算，见图10。

图10表明，设置摩擦阻尼器的框架，其地震作用相对抗震结构显著减小，因而该结构减震效果较好。

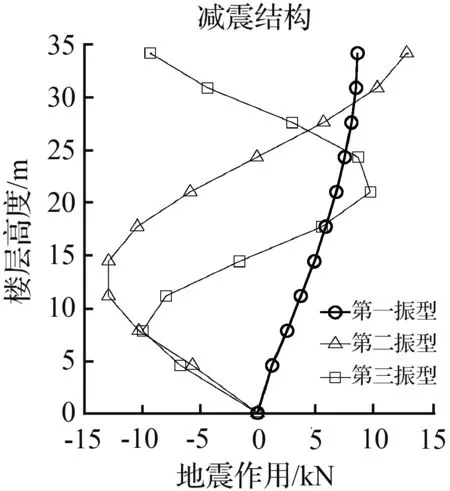
(a) OROVILLE地震波

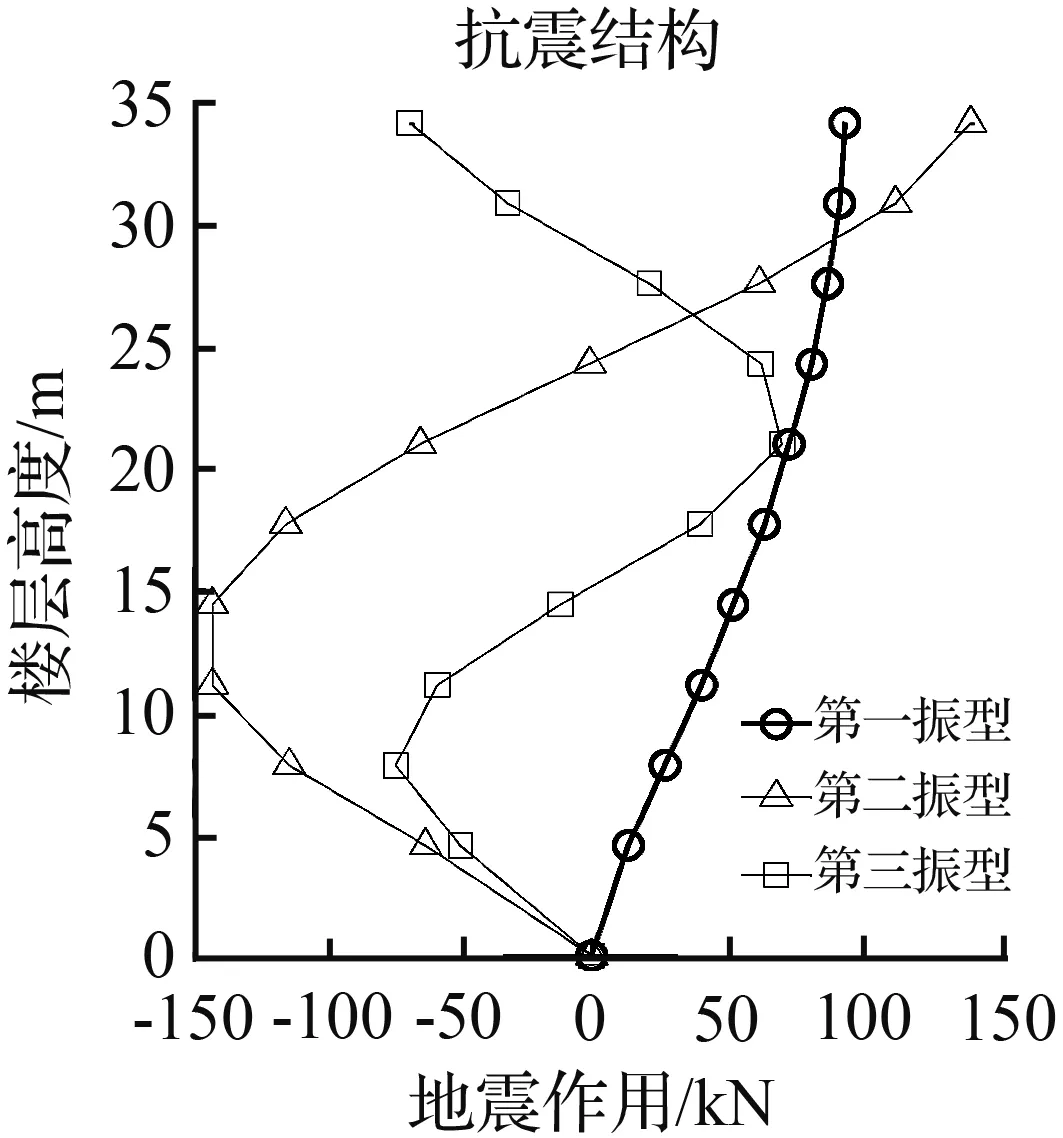
(b) EL-Centro地震波

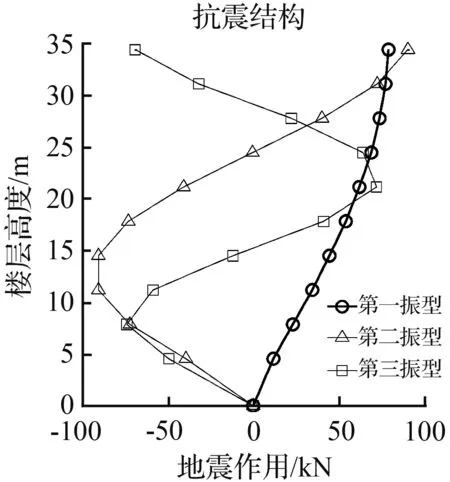
(c) HOLLYWOOD STORAGE地震波

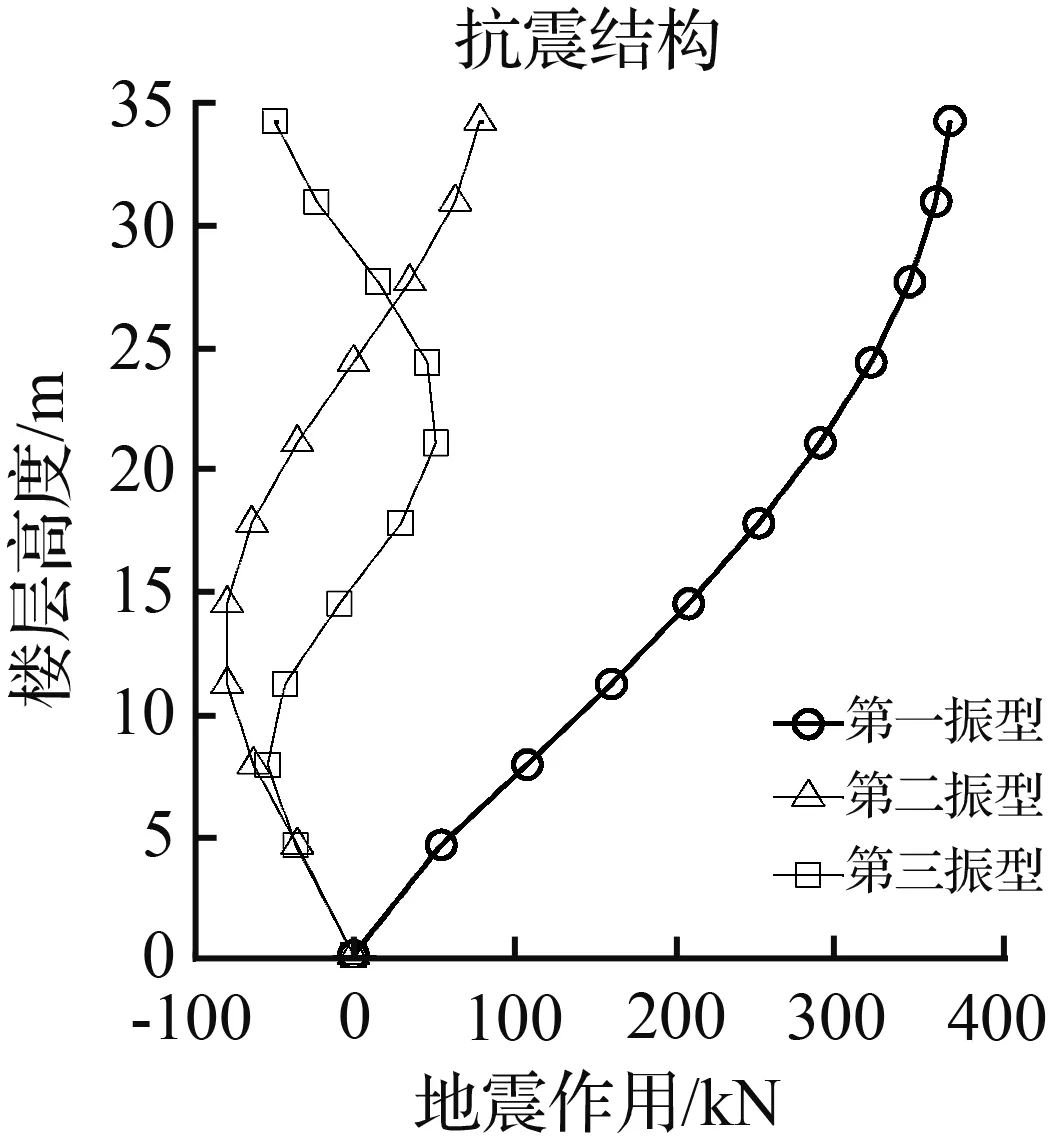
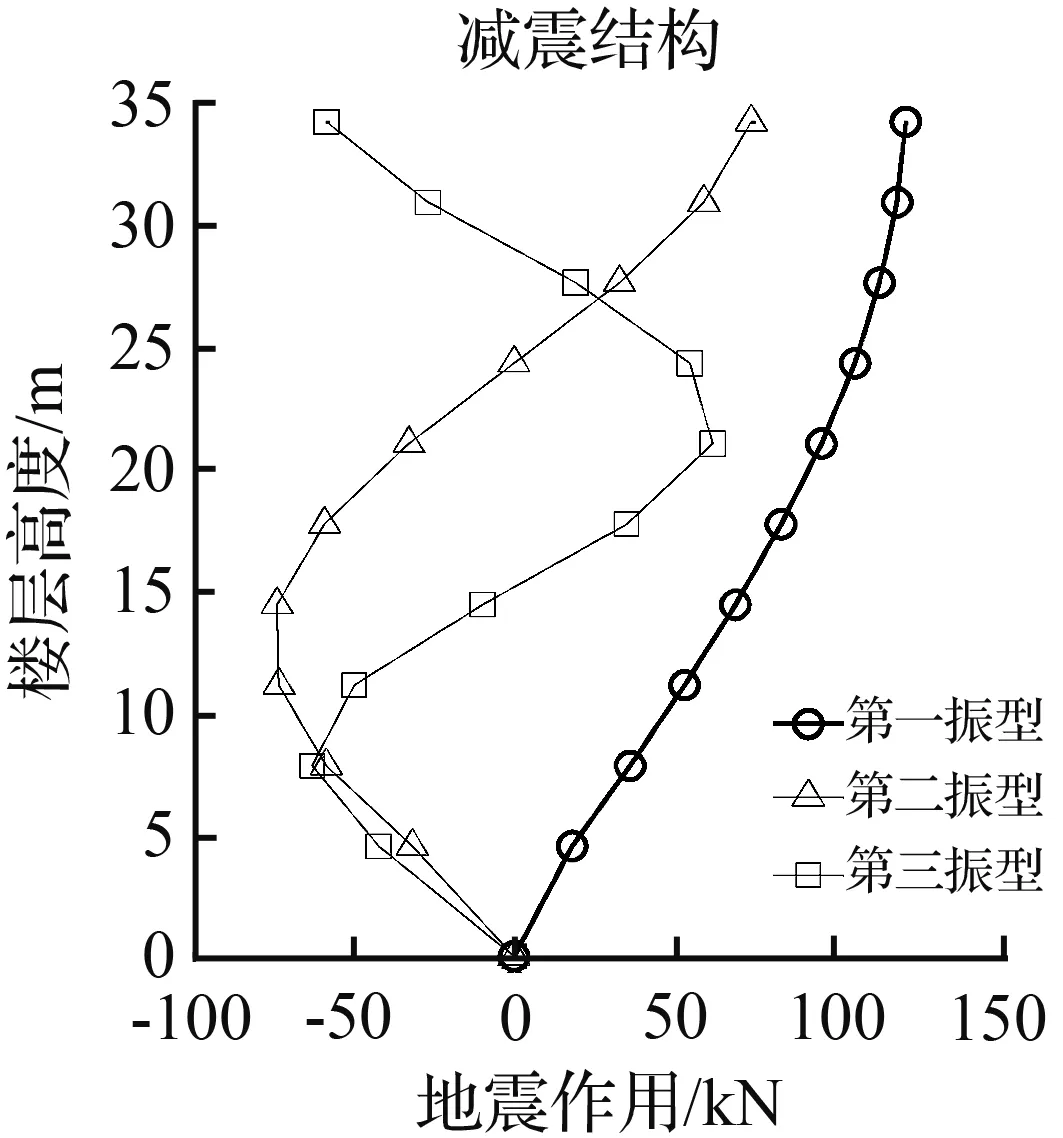
(d) 天津地震波

5 结论

根据本文分析，结论如下：

①框架结构设置摩擦阻尼器的层间最大位移角相对未设置摩擦阻尼器的框架结构，其层间最大位移角减小显著，且摩擦阻尼器对其所在楼层减震较为有效，对其他楼层减震不太明显，由此提出摩擦阻尼器在框架结构中宜连续布置，不宜间断；

②当摩擦阻尼器在结构中均匀布置时，减震效果良好，但其层间位移角分布不均匀，下部楼层较大，上部较小，由此提出各楼层阻尼力可根据式(37)进行经济布置调整。在满足建筑规范设计安全的前提下，阻尼力调整后，各楼层层间最大位移角差别降低，且下部较多楼层的层间最大位移角基本接近，由此可达到经济合理的目的，故按照本文调整方案，能更好地应用于实际工程；

③本文提出了设置摩擦阻尼器框架结构的地震作用实用计算方法，同时表明框架结构设置摩擦阻尼器后，结构各楼层地震作用大大减小；

④分析了结构各阶振动的等效阻尼比，用于计算结构各阶振动的正则坐标幅值，从而可结合《建筑抗震设计规范》给出的地震反应谱更便于计算结构地震作用。