基于SWIPT的协作中继系统动态时间分配策略
2019-08-272王哲
2王哲
(1.广西大学计算机与电子信息学院, 广西南宁530004;2.广西高校并行与分布式计算技术重点实验室, 广西南宁530004)
0 引言
能量收集(energy harvesting, EH)是解决通信系统能量受限问题的一种有效办法。通信系统中的节点利用EH技术从环境中收集部分能量并转化为电能供给自身运行,延长了系统的生命周期[1-3]。与传统能量如太阳能、风能、热能等相比,射频(radio frequency, RF)能量具有更高的可控性,广泛应用于能量收集无线网络(energy harvesting wireless network, EHWN)中[4-5]。
无线信息与能量同步传输(simultaneous wireless information and power transfer, SWIPT)技术利用RF信号同时携带能量与信息的特性,基于时分切换(time splitting, TS)和功率分流( power splitting, PS )技术使得节点能够在接收信息的同时获取能量。接收机通过调整时间切换比和功率分流比以满足节点的网络任务需求。文献[6]研究了基于PS的SWIPT系统,提出了一个根据已知瞬时信道状态动态改变功率分流比的方法,以达到信息速率和能量的均衡。文献[7]研究了基于TS和PS的SWIPT系统,根据对该系统的中断概率和信道容量进行分析,提出了一种最优时间切换比和最优功率分流比以最大化系统吞吐的策略。文献[8]基于TS的SWIPT系统进行研究,提出最优化时间切换比来达到最大化目标接收端解码信息量的目的。文献[9]研究了SWIPT系统中的共信道干扰问题,给出了接收端的最优工作切换准则以实现信息与能量传输之间的最优权衡。文献[10-12]则基于多天线技术(multiple-input multiple-output, MIMO)的SWIPT系统,针对资源分配和波束成形问题进行研究,求出了问题的最优解。从现有的研究成果可以看出,SWIPT领域的研究成果已有不少,但均是针对点对点通信系统的。文献[13]提出了基于马尔科夫决策的功率分配算法,实施对功率分配进行动态调整,以达到最大化中继网络的吞吐量的目的。
协作中继技术因具有增强数据传输的可靠性、提高吞吐量以及拓展网络覆盖的优势,得到广泛的应用。将SWIPT与协作中继技术相结合,可同时提高信息的传输速率和能量传输的可靠效率[14]。为此基于SWIPT的协作中继系统的研究应运而生。文献[15]提出了一种自适应时间切换的中继传输策略,中继的时分切换系数根据信道状态和信噪比进行动态调整,以实现系统吞吐效率最大化。研究表明,动态时间分配策略可提高中继网络的性能[16]。文献[17]基于能量收集的中继网络进行研究,提出了一种联合优化时间分配和功率分配策略以最大化系统吞吐量,但是中继收集的能量来自于太阳能、风能等传统能量,受不可控性影响较大。文献[18-19]研究了基于功率分流的中继传输策略,通过优化功率分流比以提高系统吞吐。上述的研究以提高系统吞吐为准则进行优化,并将系统的中断概率作为影响协作中继系统运行的一个重要指标。文献[20]考虑了基于SWIPT的DF中继系统,推导出系统的中断概率表达式,但是只验证了中断概率闭合解的正确性。文献[21]研究分析了时间切换中继传输策略(time splitting-based relaying, TSR)和功率分流中继传输策略(power splitting-based relaying, PSR)下的中断概率和系统吞吐,分别通过优化时间切换比和功率分流比来最小化中断概率,并考虑到优化问题的非凸性质,采用分步迭代方法得出最优解。文献[22]融合了能量收集技术和认知无线网络中的协作中继技术,提出了基于能量收集的认知协作中继系统模型,设计了一种认知协作中继传输机制。但是上述研究工作中都假定源节点至中继节点以及中继节点至目标节点这两个信息传输的时间是等分的。
本文基于SWIPT的协作中继网络模型,以中断概率作为一个目标函数,研究动态时间分配对系统中断概率的影响。在中继节点与目的节点间不同信道增益的条件下,推导出本文系统模型的中断概率与时间分配系数的表达式,以最小化中断概率为目标优化时间分配。
1 中继解码转发通信系统模型
中继解码转发通信系统模型见图1,其包含一个基站BS、一个中继节点R和1个目的节点D1。假设各信道为瑞利衰减信道,基站BS到目的节点D1由于衰落影响导致链路不可直达,要完成信息传输任务就要利用中继的协作,每个节点配置单一天线,采用半双工模式。中继节点R自身没有初始能量,当节点从基站BS发射的信号中收集完能量后会存储在自身的电池中,然后用这些已收集的能量进行解码转发。系统传输时间块结构如图2所示,T为整个传输块的周期且可划分为两个阶段,第一个阶段传输时间θT内,基站BS广播信号给中继节点,中继R采用PS策略将接收到的信号分为两部分,其中ρPs部分的信号用于能量收集,(1-ρ)Ps用于信息接收。第二个阶段传输时间(1-θ)T内,中继节点R利用收集到的能量将信息转发到目的节点,中继采用PS策略进行能量接收。
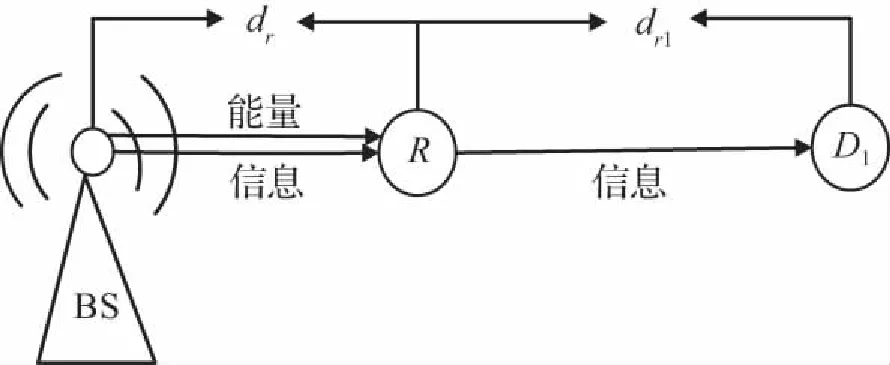
图1 中继解码转发通信系统模型
Fig.1 Model diagram of relay decoding andforwarding communication system
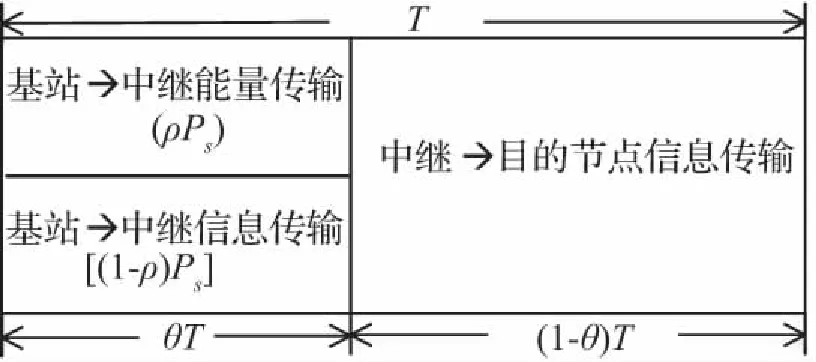
图2 系统传输块结构
Fig.2 System transmission block structure
在第一个阶段,中继节点R接收基站BS发送的信号,接收到的信号yr表示为:
(1)
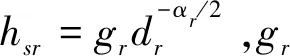
中继R收集到的能量为:
(2)
其中,η为能量转换效率系数,η∈( 0,1)。
根据香农公式可知,中继R可实现的端到端传输速率公式为:
(3)
其中,Psr=Ps/σsr2。
在第二个传输阶段,中继R用收集到的能量解码转发数据给目的节点D1,发送给目的节点D1的信号为x1。中继R传输功率表示为(不考虑噪声功率):
(4)
目的节点D1接收信号y1表示为:
(5)
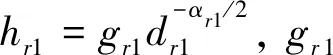
因此,目的节点D1可实现的端到端传输速率公式为:
(6)
其中,Pr1=Pr/σr12。
为了便于以下分析,假定βsr1=Ps/σr12,βsr=Ps/σsr2。
2 动态时间分配传输策略
中断作为衡量系统性能的一个重要指标,它是指由于节点的即时速率低于目标速率时发生的事件。本节将基于SWIPT的中继系统的模型进行研究分析,推导出中断概率表达式,以减小系统中断概率为目标来优化时间分配系数。
2.1 中断概率计算
中继R的信噪比用γr表示,τr表示中继节点R的目标信噪比要求;目的节点D1的信噪比用γ1表示,τ1表示D1的目标信噪比。因此中继节点R的成功概率表达式为:
Pr=Pr(γr≥τr),
(7)
而目的节点D1处的中断概率表达式为:
P1=Pr(γ1≤τ1),
(8)
对于整个系统而言,为了确保中继R可以收集足够的能量用于传输信息,假定限制:γr=τr,即BS-R链路速率达到最低速率要求,中继可以正确解码信息。由γr=(1-ρ)Psr|hsr|2=τr,可得ρ=1-τr/Psr|hsr|2。又因为Pr=ηρPs|hsr|2θ/(1-θ),所以可得Pr=max{0,η(Ps|hsr|2-τrδsr2)θ/(1-θ)},其中|hsr|2≥τr/βsr。
目的端的中断概率的表达式为:
Pout=1-P[D1],
(9)
其中,P[D1]表示目的端的成功概率。根据:γ1=Pr1|hr1|2≥τ1,所以可得到|hr1|2≥τ1/Pr1。
基站和中继之间进行无线能量与信息同步传输,要求出中继R到目的节点D1的中断概率,可先求出该链路的成功概率,如下所示:
P[D1] =Pr[(1-θ)log(1+Pr1|hr1|2)≥Rr1*,Pr1>0],
(10)
式(10)中的P[D1]可以表示如下:
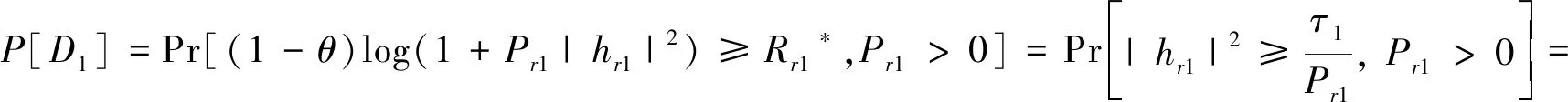
(11)
由式(11)和Pout=1-P[D1],可以得到系统的中断概率闭式表达式为:
(12)
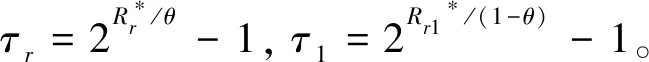
2.2 优化时间分配算法
优化时间分配算法的设计思想:根据式(12)推导出的中断概率关于时间分配系数的表达式,将最小化系统中断概率作为目标来对时间分配进行优化。目标优化函数为:
minPout, s.t. 0<θ<1, 0<ρ<1。
(13)
通过“2.1节”的分析可知,中断概率是关于时间分配系数的凸函数,存在一个最优值θ使得中断概率最小[23]。但是,目标函数包含了贝塞尔函数,这使得直接求出θ最优的值的过程比较麻烦。因此,本文采用了一种低复杂度的算法,即利用一种次优迭代的时间分配算法进行求解。算法步骤描述如下:
输入:噪声方差σsr2、σr12和基站总功率值Ps,能量转换效率η,目标速率Rr*、Rr1*,路径损失因子αr、αr1,基站BS到中继节点R的距离dr,中继R到目的节点D1的距离dr1
输出:最优时间分配值T1*、T2*
综上所述,需主动脉内球囊反搏辅助治疗的急性冠脉综合征伴严重心力衰竭患者,术前心功能4级、“罪犯”血管为左主干、术中发生无复流和术后TIMI血流<3级是影响患者预后的危险因素。对于此类患者,在主动脉内球囊反搏支持下改善心功能,减少术中无复流,提高支架术后TIMI3级血流和改善心肌水平再灌注,可能是降低患者死亡率,改善患者预后的重要手段。由于本研究为回顾性观察研究,纳入病例较少,尚需通过增加样本量及采用前瞻性研究方法进一步证实。
Step1:初始化T,n= 1,N= 1 000,θ, 集合PTotal out={}。
Step2:判断n是否小于N,若小于转step 3,若不满足n Step3:根据T1= (n/N)T;T2= (1-n/N)T;得出θ表达式。 Step4:根据式(12)计算Pout(θ)。 Step5:将计算得出的Pout(θ)添加到集合PTotal out中,n自增后转step 2。 Step6:结束。 Step7:从集合PTotal out中找到最小的Pout对应的θ。 本节对比分析本文提出的动态时间分配传输优化策略与文献[16]的PSR传输方案在不同变量的情况下的系统传输功率和中断概率,以说明本文策略在优化传输性能方面的有效性。利用Matlab R2016a进行仿真实验,假设仿真参数能量转换效率η= 0.7,路径损失因子αr= 1,αr1=2.7[16]。基站BS到中继R距离dr=0.8 m,从中继R到目的节点D1的距离dr1=2 m,噪声方差σr12=0.3,σsr2=0.1。 图3给出了两种方案在不同速率对下的传输功率与中断概率的关系。从图3中可以看出,当传输功率增加时,两种方案的中断概率会逐渐减少,整体曲线呈下降趋势。当中继节点目标速率较小时,文献[16]提出的PSR方案与本文提出的方案差距不是很大。但是当中继的目标速率增大时,本文的传输方案较文献[16]的PSR传输方案更能实现更低的中断概率,这是因为文献[16]没有对时间分配进行优化,而本文的方案采用了优化时间分配的技术。总体来看,由于本文的方案采用了动态时间分配的策略,其中断性能优于文献[16]中的PSR传输方案。 图4给出的是在基站BS到目的节点D1的不同路径损失的情况下,本文的传输优化方案和文献[16]的PSR方案在传输功率与中断概率的关系上的实验结果。当基站BS到中继R和中继R到目的节点D1的路径损失αr,αr1相差较小时,可以得出本文方案与文献[16]的PSR方案在性能上差距不是很明显;但是当路径损失增大时,本文提出的方案比文献[16]的PSR传输方案在同一传输功率下的中断概率明显减少。这是由于路径损失较大时需要合理分配时间进行传输,所以当路径损失差距较大时,本文的方案比文献[16]的PSR传输策略更能较好地提高系统的性能。这是由于路径损失较大时需要合理分配时间进行传输,所以当路径损失差距较大时,本文的方案比文献[16]的PSR传输策略能较好地减少系统中断概率,提高系统的性能。 图3 不同方案下的传输功率与中断概率的关系 图4 不同路径损失下的比较 本文基于SWIPT的协作中继系统,考虑了时间分配系数对传输的影响,提出一种动态时间分配策略进行传输优化。首先对基于SWIPT的中继系统的模型进行研究分析,推导得出中断概率与时间分配系数之间的表达式,然后以最小化中断概率为目标,优化时间分配系数,并利用迭代算法得到问题的解。仿真实验结果表明,本文所提出的传输策略比PSR传输方案能实现更小的中断概率,优化了系统传输性能,提高了系统的运行效率。3 仿真实验与性能分析
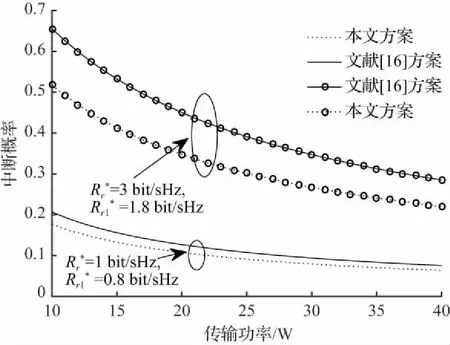
Fig.3 Relation between transmission power andinterrupt probability under different schemes
Fig.4 Comparison under different path loss4 结语
