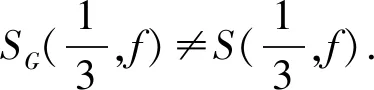度量G-空间中G-可链点集的研究
2019-08-27冀占江谭伟明粟光旺
冀占江, 谭伟明, 粟光旺
(1. 梧州学院 大数据与软件工程学院, 广西 梧州 543002; 2. 梧州学院 广西高校图像处理与智能信息系统重点实验室, 广西 梧州 543002; 3. 广西财经学院 信息与统计学院, 广西 南宁 530003)
可链点集、链等价集和链回归点集是拓扑动力系统中非常重要的概念,实际生活中有着广泛的应用,许多学者对其进行了充分的研究,得到很多有意义的成果[1-11].文献[1-2]研究了链等价集的动力学性质,文献[3-4]研究了链回归点的动力学性质,文献[5]研究了可链点集的动力学性质.通过以上文献的研究结果得知,可链点集、链等价集和链回归点集是相互联系,但是又有不同,例如对于同一点x来说,它的可链点集是链等价点集的真子集;链回归点x既是它自身的可链点又是链等价点;x的链等价点y也一定是链回归点,但是x的可链点y就不一定是链回归点.可以说在度量空中这3个点集的动力学性质已经研究得很透彻,但是在度量G-空间中,它们的性质却很少有学者进行研究.为了弄清楚他们的性质,本文选择度量G-空间中G-可链点集进行研究.首先根据度量空间中可链点集的定义,给出了度量G-空间中G-可链点集的概念,通过定义容易知道可链点集是G-可链点集的子集,但是也存在一个可链点集不等于G-可链点集的情况,本文后面给出了例子.其次通过推理,将度量空间中可链点集的性质推广到度量G-空间中的G-可链点集上,得到如下结果:
1)SG(x,f)是闭集;
2)SG(x,f)=SG(f|SG(x,f));
4)f(SG(fi(x),fn))=SG(fi+1(x),fn).
这些结果推广和改进了现有文献中可链点集的结论.
1 基本定义
定义 1设X是度量空间,f:X→X映射,称f一致连续,如果对∀ε>0,存在0<δ<ε,当d(x,y)<δ时,有d(f(x),f(y))<ε.
定义 2[12]设X是度量空间,G是拓扑群.若映射φ:G×X→X满足:
1) 对任意的x∈X,有φ(e,x)=x,其中e为G的单位元;
2) 对任意的x∈X以及g1,g2∈G,有φ(g1,φ(g2,x))=φ(g1g2,x),则称(X,G,φ)是度量G-空间,简称X是度量G-空间.为了书写方便,通常将φ(g,x)简写为gx.
特别地,若X是紧致度量空间,则称X是紧致度量G-空间.
定义 3[13]设X、Y是度量G-空间,f:X→Y连续,称f是伪等价映射,如果∀g∈G,∀x∈X,∃h∈G,有f(gx)=hf(x).
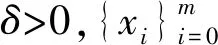
d(gif(xi),xi+1)<δ.
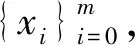
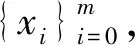
仿造度量空间中可链点集的定义,下面给出度量G-空间中G-可链点集的定义.
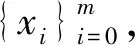
注 1通过定义易知可链点集是G-可链点集的子集,但是也存在可链点集不等于G-可链点集的情况,后面给出了例子说明了这一点.
2 若干引理
引理 1[15]设(X,d)是紧致度量G-空间,G是紧致的拓扑群,则∀ε>0,∃0<δ<ε,当d(x,y)<δ时,∀g∈G,有d(gx,gy)<ε.
引理 2设(X,d)是紧致度量G-空间,G是紧致的拓扑群,x∈X,若f:X→X同胚伪等价,则f(SG(x,f))=SG(x,f).
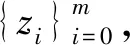
下证SG(x,f)⊂f(SG(x,f)).
设y∈SG(x,f),由引理1知,∃0<η0<η,当d(y1,y2)<η0时,∀g∈G,有
(1)
由f-1一致连续,则对η0/2>0,∃0<δ<η0,当d(y1,y2)<δ时,有
(2)
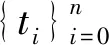
d(hn-2f(tn-2),tn-1)<δ,d(hn-1f(tn-1),y)<δ.
又f伪等价,故∃gn-1∈G使得
d(f(gn-1tn-1),y)<δ.
由(2)式知
结合d(hn-2f(tn-2),tn-1)<δ和(1)式知
因此
d(gn-1hn-2f(tn-2),f-1(y))<
d(gn-1hn-2f(tn-2),gn-1tn-1)+d(gn-1tn-1,f-1(y))<η,
则{x,t1…tn-2,f-1(y)}是f作用下的(G,η)链,故f-1(y)∈SG(x,f),因此SG(x,f)⊂f(SG(x,f)).
引理 3设(X,d)是紧致度量G-空间,G是紧致拓扑群,n∈N+,若f:X→X伪等价,则
SG(fn(x),fn)=SG(x,fn).
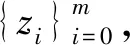
下证SG(x,fn)⊂SG(fn(x),fn).
设y∈SG(x,fn),由引理1知,∃0<ε0<ε,当d(μ,ν)<ε0时,∀g∈G,有
(3)
由fn一致连续,则对ε0/2>0,∃0<δ<ε0/2,当d(μ,ν)<δ时,有
(4)
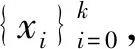
d(g0fn(x0),x1)<δ,d(g1fn(x1),x2)<δ.
由f伪等价和(4)式知,∃h0∈G使得
由(3)式知
因此
d(g1h0f2n(x0),x2) d(g1fn(x1),x2)<ε. 故{fn(x),x2…xk-1,y}是fn作用下的(G,ε)链,则y∈SG(fn(x),fn),因此SG(x,fn)⊂SG(fn(x),fn). 定理 1设(X,d)是度量G-空间,x∈X,若f:X→X连续,则SG(x,f)是闭集. 故 d(gm-1f(xm-1),y)≤d(gm-1f(xm-1),z)+d(z,y)<η. 因此{x,x1…xm-1,y}是(G,η)链,则y∈SG(x,f),因此SG(x,f)是闭集. 定理 2设(X,d)是紧致度量G-空间,G是紧致的拓扑群,x∈X,若f:X→X连续,则 SG(x,f)=SG(f|SG(x,f)). 证明显然SG(f|SG(x,f))⊂SG(x,f).下证SG(x,f)⊂SG(f|SG(x,f)).设y∈SG(x,f). 反证法.若不然∃η0>0,存在包含SG(x,f)的开集U0,对任意在f作用下的从x到y(G,η0)链,至少有一个元素不在在U0中.取正数序列{ηk}k≥1,且满足ηk<η0,k≥1,ηk→0.因此对f作用下的从x到y(G,ηk)链,必有一个元素不在在U0中,不妨记为zk.由X的紧致性,设zk→z.由于X-U0是闭集,故z∈X-U0.固定m>0且满足ηm<η/2和d(zm,z)<η/2.设{t0,t1,…tm,tm+1…tl-1,tl}是上面的提到的(G,ηm)链,其中,t0=x,tl=y,tm=zm∉U0.故对∀0≤i d(gif(ti),ti+1)<ηm. 特别地 d(gm-1f(tm-1),tm)<ηm. 故d(gm-1f(tm-1),z)<η.因此{t0,t1,…tm-1,z}是f作用下的(G,η)链,故z∈SG(x,f),这与z∈X-U0矛盾,故(*)成立. 由引理1知,∀η>0,∃0<δ0<η,当d(μ,ν)<δ0时,∀g∈G,有 (5) 由f一致连续,则对δ0/3>0,∃0<δ1<δ0/3,当d(μ,ν)<δ1时,有 (6) d(gif(yi),yi+1)≤d(gif(yi),gif(xi))+ d(gif(xi),xi+1)+d(xi+1,yi+1)<η. 因此y∈SG(f|SG(x,f)). 令 C0={x,f(x)…fi0(x),fi0+1(x)…fn+i0-1(x)}, Ci={xi,f(xi)…fn-1(xi),xi+1}, 1≤i≤l-1,C=C0C1C2…Cl-1, 则C是f作用下的(G,ε)链,故y∈SG(x,f). ∀η>0,由引理1知,∃0<η0<η/2n,当d(μ,ν)<η0时,∀g∈G,有 (7) 对0≤j<2n,由fj一致连续,对η0>0,∃0<δ<η0,当d(μ,ν)<δ时,有 d(fj(μ),fj(ν))<η0. (8) Bi={y0,y1,y2,…,ym}, 1≤i≤n, B=B1B2…BnB0. d(hif(zi),zi+1)<δ. 特别地 ⋮ 由(7)式和G可交换知 ⋮ 故 即 同理,对任意的1≤i≤p-1,∃gi∈G使 d(gifn(zin+r),z(i+1)n+r)<η. 因此{fr(x),zn+r,z2n+r,…,zpn+r}是fn作用下的(G,η)链.故y∈SG(fr(x),fn),则 定理 4设(X,d)是紧致度量G-空间,G是紧致拓扑群,n∈N+,0≤i≤n-1,若f:X→X同胚伪等价,则 f(SG(fi(x),fn))=SG(fi+1(x),fn). 证明∀η>0,由f一致连续知,∃0<δ<η,当d(μ,ν)<δ时,有 d(f(μ),f(ν))<η. (9) d(hjfn(zj),zj+1)<δ. 又f伪等价和(9)式知,∃lj∈G使 d(ljfn+1(zj),f(zj+1))<η, f(SG(fi(x),fn))⊂SG(fi+1(x),fn). 由引理2知 SG(fi+1(x),fn)=fn(SG(fi+1(x),fn)). 由引理3知 SG(fn+i(x),fn)=SG(fi(x),fn). 又fn-1(SG(fi+1(x),fn))⊂SG(fn+i(x),fn),故 SG(fi+1(x),fn)=fn(SG(fi+1(x),fn))⊂ f(SG(fn+i(x),fn))=f(SG(fi(x),fn)). 因此SG(fi+1(x),fn)⊂f(SG(fi(x),fn)),故SG(fi+1(x),fn)=f(SG(fi(x),fn)). 由定义知道可链点集是G-可链点集的子集,下面的例子说明,可链点集是G-可链点集的真子集,从而G-可链点集不是平凡的推广. d(x,y)=|x-y|,x,y∈X, 则(X,d)是度量空间.取拓扑群G≡Z2={-1,1},按如下方式定义φ:G×X→X, φ(1,x)=x,φ(-1,x)=1-x,x∈X, 则(X,d,G)是度量G-空间.定义f:X→X,f(x)=x,x∈G,则f是连续的.根据可链点集和G-可链点集定义知: 致谢梧州学院校级科研项目(2017C001)对本文给予了资助,谨致谢意.3 主要定理

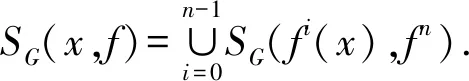


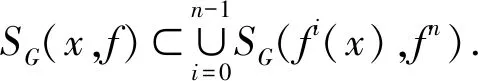
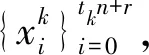
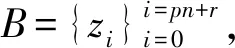


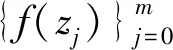
4 总结