基于符号检测辅助的干扰对齐算法∗

贾国庆，王路

(青海民族大学物理与电子信息工程学院，青海西宁810007)

0 引言

为减轻蜂窝移动网络中的小间距干扰（inter-cell interference，ICI），研究人员已经注意到一种相对较新的技术，即干扰对齐（IA）[1,2]．干扰对齐作为一种干扰消除技术，可以获得干扰信道自由度的最佳值，从而有效改善系统的性能．其思想是通过在发送信息前给每个用户的信号进行预编码，使从任意一个接收用户看来，它收到的干扰信号都在一个子空间上，而来自期望用户的有用信号都在另一正交子空间上，然后通过正交投影迫零就可以消除干扰[3−5]．

然而为了实现干扰对齐，发射机和接收机必须联合设计，这通常是很难实现的．在不同优化标准的基础上，业界提出了大量的迭代收发器设计方法[6−8]．目前基于迭代求解预编码矩阵与接收端的干扰抑制矩阵的方法主要有最小均方误差（minimum mean square error，MMSE）、最小二乘算法(LS)、最大信干噪比算法(MAXSINR)等等[9−11]．

在对基于符号检测辅助的MMSE干扰对齐算法[12]有了较为深入的研究后，本文提出了基于符号检测辅助的最小二乘法(SDA-LS)、最大信干噪比(SDA-MAX-SINR)干扰对齐迭代算法，以及基于符号检测辅助的最小二乘法和最大信干噪比相结合的干扰对齐算法（SDA-LS+MAX-SINR）．然后利用系统仿真验证了文中所提的三种干扰对齐算法在系统的均方误差（mean square error，MSE）和误码率(bit error rate,BER)上的性能均有明显的改善，并且其算法的复杂度也有显著的降低．

1 系统模型

在K用户的MIMO（多输入多输出）干扰信道中，每个带有N个天线的发射机通过发端发送d个独立码流与相应的带有M个天线的接收机通信．

图1 多用户干扰信道模型Fig 1 Multi-user interference channel model

假设第i个接收机只能接收第i个发射机的发射信号，而将其他发射机发射的信号视为干扰信号，则第i个接收机接收到的信号为：

yi∈CM×1是第i个节点接收到的信号；Hi,j∈CM×N(CM×N表示M×N维的复数域)表示从第j个发射机发射到第i个接收机的信道；Vj∈CN×d是在第j个发射机发射上的预编码矩阵；sj∈Cd×1是通过第j个发射机的发送信号；ni∈CM×1代表均值为零、方差为σ2的循环对称的加性高斯白声．在本文中我们定义γ=P/σ2为的信噪比，P是发射功率．为了能将发射机的信号恢复出来，在接收机端处加入一个迫零矩阵（H表示矩阵的共轭转置），从而接收机端的接收信号为

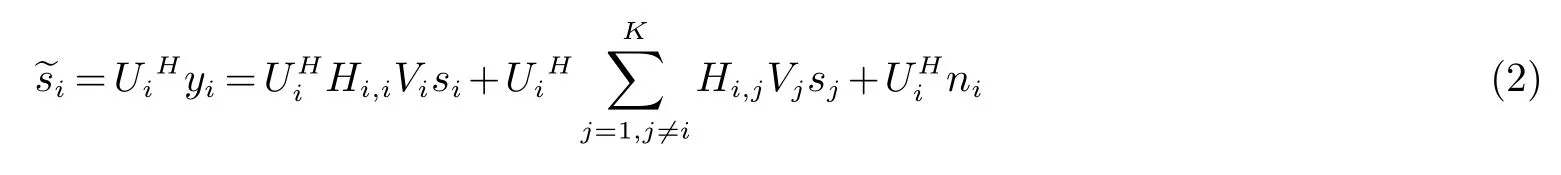
Ui指定为干扰抑制矩阵（合并器），在接收端采用简单的迫零均衡就可以完全消除干扰．假设rank(F)表示矩阵F的秩，则rank(Hi,iVi)表示有用信号的秩，即为期望信号所占用的空间维数．rank(Hi,jVj)则表示干扰信号所占空间的秩为di（di表示第i个发射机发送的独立的数据流的个数），干扰信号所占空间的秩为0[12−15]．故完美的干扰对齐条件为：

2 传统LS、MAX-SINR的IA算法

2.1 LS传统IA算法

LS算法在算法设计中将噪声看为零即可．根据式（2），我们容易模拟出合适Ui可以表示为：

定义矩阵函数为fUi为:

从而最佳的Ui可以由条件=0得到：

此时，将焦点集中在相同条件下通过利用Ui和Vi轮流作为预编码器和合并器来获得预编码矩阵，得到：

所以可以得到最佳的Ui和Vi如下：

传统的LS算法步骤总结如下表1所示．

表1 传统LS算法Tab 1 Traditional LS algorithm

2.2 MAX-SINR传统IA算法

MAX-SINR算法是以最大化接收端码字SINR(信干噪比)为原则的干扰对齐算法．根据系统模型，第i个用户接收到的第l个码字的解调信息为（()lo表示取矩阵的第l行）

传统算法中，考虑到符号码流s不能跟滤波器矩阵的求解有关联，所以通过求码流s的均值而消除码流的影响．一般情况下，符号流sj满足等式（9）．有效信号分量为：()lo(Hi,j)(Vi)ol(Si)l.有效信号的功率对码流求均值后：

干扰信号和噪声分量为:

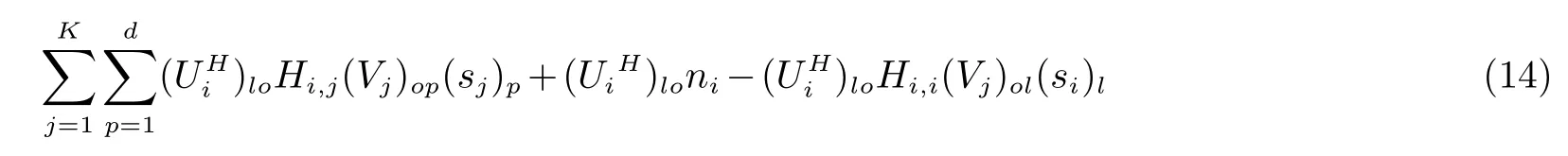
干扰信号和噪声功率（对码流及噪声求均值后）为：

则正向链路干扰及噪声的互相关矩阵(Bi)l为：

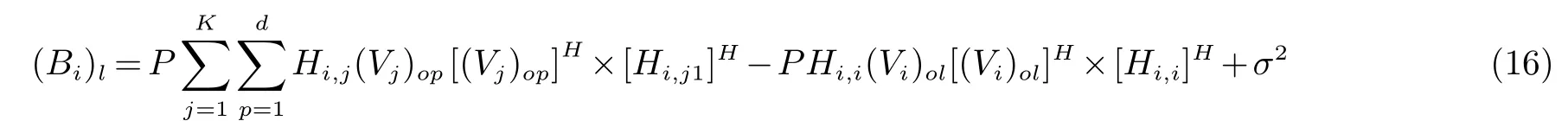
从而第i个用户的第l个码流的SINR可以表示为：

信干噪比最大时，最优的干扰抑制矩阵为：

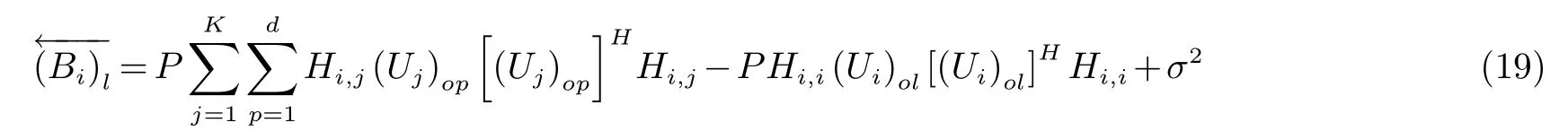
信干噪比最大时，最优的预编码矩阵为：

传统MAX-SINR算法步骤总结如表2所示．

表2 传统MAX-SINR算法Tab 2 Traditional MAX-SINR algorithm

3 SDA-LS、SDA-MAX-SINR、SDA-LS+MAX-SINR算法

3.1 SDA-LS算法

实际上，通过对等式（7）、（8）期望得到的等式（10）、（11）并不是严格对于后者的，尤其是当总的传输数据流不够大时．给出一种基于等式（7）、（8）的通过使sj=j的改进算法，得到如下公式：

但是，如果等式（21）、（22）同等式（2）直接用于迭代计算，IA的性能将由于大量信号检测错误而显著降低．首先让基于等式的（10）、（11）做迭代运算后，再让等式（21）、（22）与等式（2）做迭代运算，IA的性能就会显著提高．SDA-LS算法步骤总结如表3所示．

表3 SDA-LS算法Tab 3 SDA-LS algorithm

3.2 SDA-MAX-SINR算法

首先求改进的SDA-MAX-SINR算法的有用信号的功率及干扰信号和噪声的功率．有用信号的功率为：

干扰信号和噪声功率（对噪声求均值后）为：

其中正向链路干扰及噪声的互相关矩阵(Bi)l为：

从而基于符号检测的MAX-SINR算法中的SINR可以表示为：

此时最优的干扰抑制矩阵为：

反转信道，令(Vi)lo=，则反向链路的干扰及噪声的互相关矩阵为

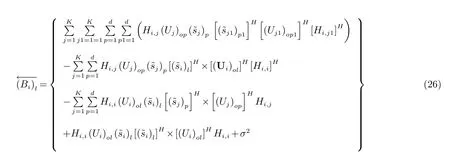
则最优预编码矩阵为：

SDA-MAX-SINR算法步骤总结如表4所示．

表4 SDA-MAX-SINR算法Tab 4 SDA-MAX-SINR algorithm

3.3 SDA-LS+MAX-SINR算法

由表5可知，SDA-LS算法的复杂度最低，SDA-MAX-SINR算法的复杂度最高．所以基于前面的SDA-LS和SDA-MAX-SINR两种算法，将两种算法结合．在这里提出一种结合的SDA-LS+MAX-SINR算法，用于降低复杂度．从表5可以看出SDA-LS+MAX-SIN算法的复杂度约等于SDA-LS算法的复杂度，并且比SDA-MAX-SINR算法降低了11%．

表5 算法的复杂度分析Tab 5 Analysis of the complexity of the algorithm

根据前面SDA-LS算法SDA-MAX-SINR算法的步骤，将两种算法相结合．首先让等式（21）、（22）与等式（2）做迭代运算后，再让等式（25）、（27）与等式（2）做迭代运算．这样就得到了SDA-LS+MAX-SINR算法．IA的性能会显著提高，其算法复杂度也降低了不少．具体步骤如表6所示．

表6 SDA-LS+MAX-SINR算法Tab 6 SDA-LS+MAX-SINR algorithm

4 仿真结果

K=3，N=4，M=4，d=2，选择正交相移键控（quadrature phase shift keying,QPSK）调制解调方式，信噪比SNR采用0dB、5dB、15dB、20dB进行比较，性能仿真参数取迭代值1 000；信道为加性高斯白噪声信道．利用MATLAB对基于符号检测辅助的干扰对齐算法、传统干扰对齐算法的MSE和BER进行比较，结果如图2、图3所示．

图2 不同SNR下的传统和改进算法的MSE随迭代次数变化的曲线Fig 2 Traditional and different SNR Curve of MSE with improved iterations of improved algorithm

图3 传统和改进算法的误码率对比曲线Fig 3 Comparison of bit error rate curves between traditional and improved algorithms

从图2可以看出，在同一信噪比下，MAX-SINR算法的MSE最低，LS算法的MSE最高，LS+MAX-SINR算法的MSE介于MAX-SINR算法与LS算法之间，略低于LS算法，并且传统算法迭代到一定次数时已经收敛，系统的MSE几乎不再有降低的可能性；此时采用改进算法，初始时由于检测信号及信道的不稳定性，三种算法的MSE均略高于传统算法，随着迭代次数的增加，可以看出，SDA-LS算法的MSE最高，SDA-MAX-SINR算法的MSE最低，而改进算法SDA-LS+MAX-SINR的MSE性能有了很大改善，并且基本与SDA-MAX-SINR算法的MSE相同．

从图3可以看出，在本文采用的5种SNR中，SDA-LS算法、SDA-MAX-SINR算法、SDA-LS+MAX-SINR算法的BER均低于LS算法、MAX-SINR算法、SDA-LS+MAX-SINR算法；而且信噪比越低，改进算法的系统性能越好．SDA-LS+MAX-SINR算法和SDA-MAX-SINR算法的BER基本持平，并且SDA-LS+MAX-SINR算法的BER低于SDA-LS算法．这说明结合算法在降低复杂度的同时，并没有改变MSE的性能．

5 结束语

本文在传统的LS、MAX-SINR干扰对齐算法的基础上，提出了改进的迭代算法，即SDA-LS、SDA-MAXSINR迭代算法；又根据SDA-LS和SDA-MAX-SINR两种改进的迭代算法，提出了一种改进的结合迭代算法，即SDA-LS+MAX-SINR迭代算法．通过理论分析和仿真可以得到提出的算法在MSE和BER均有较大的改进，而且结合的算法在复杂度以及MSE和BER上结合了SDA-LS和SDA-MAX-SINR两种算法的优点．